北师大版七年级上册数学:第四章 基本平面图形同步习题课件(115张PPT)
文档属性
| 名称 | 北师大版七年级上册数学:第四章 基本平面图形同步习题课件(115张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-16 10:38:48 | ||
图片预览









文档简介
第四章 基本平面图形
数学·七年级上册·北师
1 线段、射线、直线
1.[2020广东佛山禅城区期末]手电筒射出的光线给我们的形象是 ( )
A.直线 B.射线 C.线段 D.折线
答案
1.B 【解析】 手电筒射出的光线可以抽象成射线.故选B.
知识点1 线段、射线、直线的概念
2.学校升国旗用的旗杆给我们的形象是 ( )
A.直线 B.射线
C.线段 D.折线
答案
2.C 【解析】 升国旗用的旗杆可以抽象成一条线段.故选C.
知识点1 线段、射线、直线的概念
3.下列说法中,正确的是 ( )
A.直线虽然没有端点,但长度是可以度量的
B.射线只有一个端点,但长度是可以度量的
C.线段虽然有两个端点,但长度却是可以变化的
D.只有线段的长度是可以度量的,直线、射线的长度不可以度量
答案
3.D
知识点1 线段、射线、直线的概念
4.下列各线段的表示方法中,正确的是 ( )
A.线段A B.线段ab
C.线段AB D.线段Ab
答案
4.C 【解析】 本题考查线段的表示方法,线段可以用一个小写字母表示,也可以用端点处的两个大写字母表示.故选C.
知识点2 线段、射线、直线的表示方法及画法
5.[2020天津和平区期末]下列语句中,正确的有 ( )
①直线MN与直线NM是同一条直线;
②射线AB与射线BA是同一条射线;
③线段PQ与线段QP是同一条线段;
④直线上一点把这条直线分成的两部分都是射线.
A.1个 B.2个 C.3个 D.4个
答案
5.C 【解析】 ②射线AB与射线BA,二者端点不同,不是同一条射线,故②不正确,正确的是①③④,共3个.故选C.
知识点2 线段、射线、直线的表示方法及画法
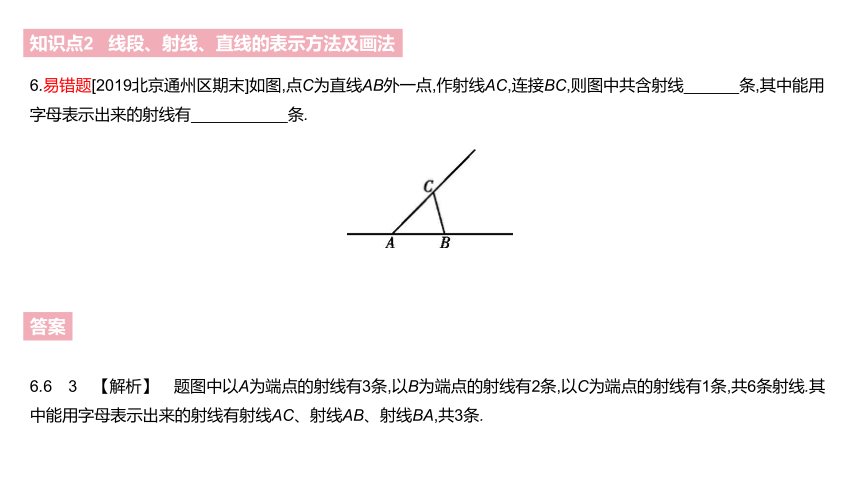
6.易错题[2019北京通州区期末]如图,点C为直线AB外一点,作射线AC,连接BC,则图中共含射线 条,其中能用字母表示出来的射线有 条.?
答案
6.6 3 【解析】 题图中以A为端点的射线有3条,以B为端点的射线有2条,以C为端点的射线有1条,共6条射线.其中能用字母表示出来的射线有射线AC、射线AB、射线BA,共3条.
知识点2 线段、射线、直线的表示方法及画法
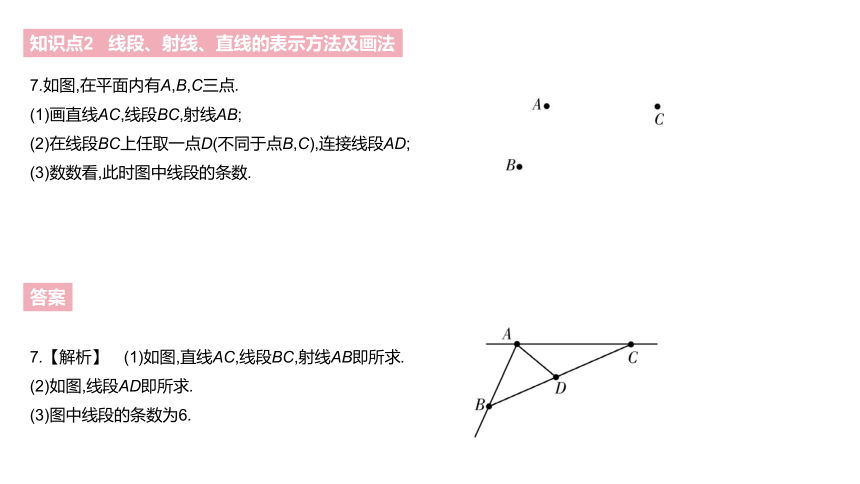
7.如图,在平面内有A,B,C三点.
(1)画直线AC,线段BC,射线AB;
(2)在线段BC上任取一点D(不同于点B,C),连接线段AD;
(3)数数看,此时图中线段的条数.
答案
7.【解析】 (1)如图,直线AC,线段BC,射线AB即所求.
(2)如图,线段AD即所求.
(3)图中线段的条数为6.
知识点2 线段、射线、直线的表示方法及画法
8.[2020广东佛山期末]在墙壁上固定一根横放的木条,至少需要钉子的枚数是 ( )
A.1 B.2 C.3 D.4
答案
8.B 【解析】 根据两点确定一条直线,可知固定一根横放的木条,至少需要2枚钉子.故选B.
知识点3 直线的基本事实(两点确定一条直线)
9.下列现象中,可以用直线的基本事实“经过两点有且只有一条直线”来解释的有 ( )
①农民伯伯拉秧绳插秧;②园林工人栽一行树,先栽首尾的两棵树;③木匠师傅弹墨线.
A.0个 B.1个 C.2个 D.3个
答案
9.D
知识点3 直线的基本事实(两点确定一条直线)
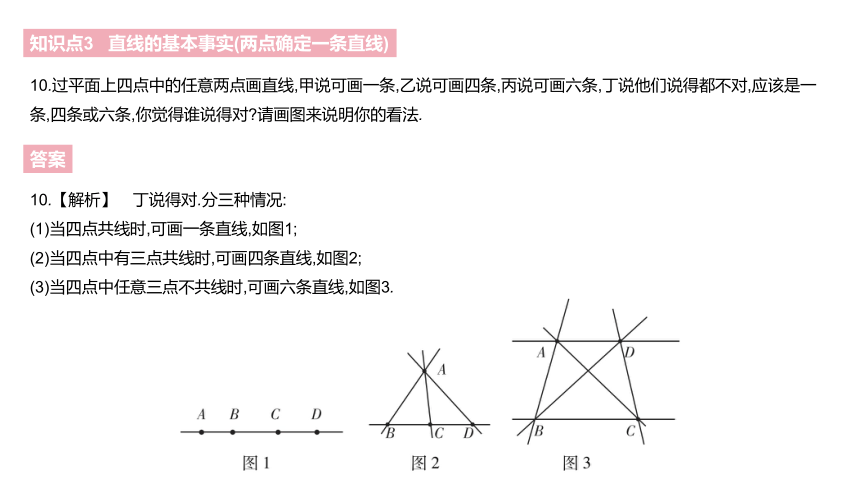
10.过平面上四点中的任意两点画直线,甲说可画一条,乙说可画四条,丙说可画六条,丁说他们说得都不对,应该是一条,四条或六条,你觉得谁说得对?请画图来说明你的看法.
答案
10.【解析】 丁说得对.分三种情况:
(1)当四点共线时,可画一条直线,如图1;
(2)当四点中有三点共线时,可画四条直线,如图2;
(3)当四点中任意三点不共线时,可画六条直线,如图3.
知识点3 直线的基本事实(两点确定一条直线)
1.如图所示,下列说法不正确的是 ( )
A.直线AC经过点A
B.射线DE与直线AC有公共点
C.点F在直线AC上
D.线段AC与线段BD相交于点C
答案
1.D
2.[2020北京房山区期末]下列各项所给的线段、射线、直线能相交的是 ( )
答案
2.B
3.如图,点A,B,C在直线l上,则图中直线、线段、射线的条数分别为 ( )
A.3,3,3
B.1,2,3
C.1,3,6
D.3,2,6
答案
3.C 【解析】 题图中直线有1条;线段有AB,AC,BC,共3条;以A为端点的射线有2条,以B为端点的射线有2条,以C为端点的射线有2条,共6条射线.故选C.
4.观察下列图形,并阅读相关文字,则20条直线相交,交点个数最多是 ( )
A.190
B.210
C.380
D.420
答案
4.A 【解析】 由题图可以发现,2条直线相交最多有1个交点,3条直线相交最多有1+2=3个交点,4条直线相交最多有1+2+3=6个交点,所以20条直线相交最多有1+2+3+?+19=190个交点.故选A.
5.如图是射击比赛的图片,为了准确地击中靶心,运动员要进行瞄准,那么瞄准的数学原理是 .?
答案
5.两点确定一条直线
6.[2019江西抚州期中]如图,记以点A为端点的射线条数为x,以点D为其中一个端点的线段的条数为y,则x-y的值为 .?
答案
6.-2 【解析】 以点A为端点的射线有:射线AC,射线AB.所以x=2.以点D为其中一个端点的线段有:线段DA,线段DO,线段DB,线段DC.所以y=4,所以x-y=2-4=-2.
7.如图,数轴上的原点为O,点A表示3,点B表示-32.
(1)数轴是什么图形?
(2)数轴在原点O右边的部分(包括原点)是什么图形?怎样表示?
(3)射线OB上的点(除点O外)表示什么数?端点表示什么数?
(4)数轴上表示不小于-32且不大于3的部分是什么图形?怎样表示?
?
答案
7.【解析】 (1)数轴是直线.
(2)数轴在原点O右边的部分(包括原点)是射线,表示为射线OA.
(3)射线OB上的点(除点O外)表示负数,端点O表示0.
(4)数轴上表示不小于-32且不大于3的部分是线段,表示为线段BA或线段AB.
?
8.(1)如图1,直线上有2个点,则图中有 条可用图中字母表示的射线,有 条线段;?
(2)如图2,直线上有3个点,则图中有 条可用图中字母表示的射线,有 条线段;?
(3)如图3,直线上有n个点,则图中有 条可用图中字母表示的射线,有 条线段;?
(4)应用(3)中的发现,若火车的行驶路线上有20个车站,火车在这条线路上往返行车,需要印制多少种火车票?
答案
8.【解析】 (1)2 1
(2)4 3
(3)(2n-2) ????(?????1)2
以每个点为端点,左、右各有一条射线,所以有n个点就有2n条射线,而射线需用2个大写字母表示,所以最左边和最右边的射线无法表示,所以可以用题图中字母表示的射线有(2n-2)条.线段条数有如下规律:2个点时有1 条;3个点时有3条(3=1+2);4个点时有6条(6=1+2+3),所以n个点时有1+2+3+4+5+?+(n-1)=????(?????1)2(条).
(4)火车售票问题可以抽象成直线上有20个点时的线段条数问题.
因为火车往返行车,所以由(3)知有n(n-1)种火车票,
把n=20代入可知,需要印制20×(20-1)=380种火车票.
?
2 比较线段的长短
1.下列现象可用“两点之间线段最短”来解释的是 ( )
A.用两个钉子就可以把木条固定在墙上
B.正常情况下,射击时要保证瞄准的一只眼在准星和缺口确定的直线上,才能射中目标
C.从A地到B地架设电线,总是尽可能沿着线段AB架设
D.以上都不可以
答案
1.C 【解析】 A项和B项体现的是“两点确定一条直线”,C项体现的是“两点之间线段最短”.故选C.
知识点1 线段的基本事实(两点之间线段最短)
2.[2020江西南昌东湖区期末]如图,把三角形剪去一个角,所得四边形的周长比原三角形的周长小,能正确解释这一现象的数学知识是 ( )?
A.四边形周长小于三角形周长
B.两点确定一条直线
C.两点之间线段最短
D.经过一点有无数条直线
答案
2.C
知识点1 线段的基本事实(两点之间线段最短)
3.如图,设A,B,C,D为四个居民小区,现要建一个购物中心,试问把购物中心建在何处,才能使四个居民小区到购物中心的距离之和最小.请说明理由.
答案
3.【解析】 连接AD,BC 交于一点,该点即购物中心的位置.因为两点之间线段最短,到A,D距离之和最小的点在线段AD上,到B,C距离之和最小的点在线段BC上,所以到A,B,C,D距离之和最小的点就是线段AD和线段BC的交点.
知识点1 线段的基本事实(两点之间线段最短)
4.下列说法正确的是 ( )
A.过A,B两点的直线的长度是A,B两点间的距离
B.线段AB就是A,B两点间的距离
C.在连接A,B两点的所有线的长度中,最短的是A,B两点间的距离
D.乘高铁从上海到北京要走1 318千米,所以上海站与北京站之间的距离是1 318千米
答案
4.C 【解析】 两点间的距离指的是连接两点的线段的长度,故A项和B项错误,D项,乘高铁所走的路线不一定是线段,故D项错误.故选C.
知识点2 两点之间的距离
5.如果A,B,C三点在同一直线上,且线段AB=4 cm,BC=2 cm,那么A,C两点之间的距离是多少?
答案
5.【解析】 分两种情况.
(1)当点C在线段AB上时,如图1所示,AC=AB-BC,因为AB=4 cm,BC=2 cm,所以AC=4-2=2(cm);
?
(2)当点C在线段AB的延长线上时,如图2所示,AC=AB+BC,因为AB=4 cm,BC=2 cm,所以AC=4+2=6(cm).
知识点2 两点之间的距离
6.下列作图语句中,正确的是 ( )
A.作直线AB=3 cm
B.延长线段AB至点C,使 BC=AB
C.延长射线OA至点B,使AB=OA
D.作直线使之经过A,B,C三点
答案
6.B 【解析】 直线是向两方无限延伸的,所以不可度量,A项错误;射线OA是从端点O向A无限延伸的,所以只能反向延长射线OA,C项错误;当A,B,C三点不在同一条直线上时,无法作出一条直线能经过A,B,C三点,D项错误.故选B.
知识点3 利用尺规作图作线段
尺规作图语言表达的准确性
在尺规作图中,要求准确表达,由于直线和射线是无限延伸的,故不能出现延长直线或延长射线这样的描述,也不能作出有长度的直线和射线,同时要注意作图的合理性.
7.如图,已知线段a,b(a>b),按要求用尺规作图,并写出作图步骤.
(1)求作线段c,使c=a-b;
(2)求作线段d,使d=a+2b.
答案
7.【解析】 (1)作射线AD;用圆规在射线AD上截取AB=a;在线段AB上截取BC=b.则线段AC就是所求作的线段c,如图所示.
?
(2)作射线EI;用圆规在射线EI上顺次截取EF=a,FG=GH=b.则线段EH就是所求作的线段d,如图所示.
知识点3 利用尺规作图作线段
8.[2019北京海淀区期末]如图,用圆规比较两条线段AB和A'B'的长短,其中正确的是 ( )?
A.A'B'>AB
B.A'B'C.A'B'=AB
D.无法比较
答案
8.B
知识点4 线段长短的比较
9.已知AB=6,下列四个选项能确定点C是线段AB的中点的是 ( )
A.BC=3 B.AC+BC=6
C.AC=BC=3 D.AB=2AC
答案
9.C 【解析】 当BC=3时,点C不一定在线段AB上,A项错误;当点C在线段AB上任意的位置时,AC+BC=6都成立,B项错误;当AC=BC=3时,点C一定是线段AB的中点,C项正确;当AB=2AC时,AC=3,但点C不一定在线段AB上,D项错误.故选C.
知识点5 线段的中点
10.[2020山东临沂河东区期末]如图,已知线段AB,C是线段AB上一点,M是AB的中点,N是AC的中点.
(1)若AB=8,AC=3.2,求线段MN的长;
(2)若BC=a,试用含a的式子表示线段MN的长.
知识点5 线段的中点
答案
10.【解析】 (1)因为AB=8,M是AB的中点,
所以AM=12AB=4.
因为AC=3.2,N是AC的中点,
所以AN=12AC=1.6,
所以MN=AM-AN=4-1.6=2.4.
(2)因为M是AB的中点,
所以AM=12AB.
因为N是AC的中点,
所以AN=12AC,
所以MN=AM-AN=12AB-12AC=12(AB-AC)=12BC=12a.
?
知识点5 线段的中点
1.如图,C,B是线段AD上的两点,若AB=CD,BC=2AC,则AC与CD的关系为 ( )
A.CD=2AC
B.CD=3AC
C.CD=4AC
D.不能确定
答案
1.B 【解析】 因为AB=CD,所以AB-BC=CD-BC,即AC=BD.因为BC=2AC,所以CD=3AC.故选B.
2.[2020湖北武汉汉阳区期末]如图,线段CD在线段AB上,且CD=3,若线段AB的长是正整数,则图中所有线段长的和可能是 ( )?
A.28
B.29
C.30
D.31
答案
2.C 【解析】 由题意,知所有线段长之和=AC+AD+AB+CD+CB+BD=AC+AC+3+AC+3+BD+3+3+BD+BD= 12+ 3(AC+ BD)=12+3(AB-3)=3AB+3=3(AB+1),因为AB是正整数,所以所有线段之和是3的倍数.故选C.
3.如图,线段AB上有两点C和D,其中AC∶BC=3∶4,AD∶DB=2∶5,且CD=2 cm,则线段AB的长为 ( )
A.12 cm
B.14 cm
C.16 cm
D.18 cm
答案
3.B 【解析】 设AC=3x,则BC=4x,所以AB=AC+BC=7x.因为AB=AD+DB,AD∶DB=2∶5,所以AD=2x,DB=5x,则CD=AC-AD=3x-2x=x=2 cm,所以AB=7×2=14(cm).故选B.
选择计算线段长度的方法的思路
计算线段的长度时,通常根据题中给定的条件,结合图形进行解答.一般考虑采用逐段计算法.若待求线段无法用已知线段的和或差表示出来,则考虑用整体计算法.若题中存在几条线段之间的比例关系时,则考虑运用方程思想求解.
4.已知线段MN=10 cm,点C是直线MN上一点,NC=4 cm,若P是线段MN的中点,Q是NC的中点,则线段PQ的长度是
cm.?
答案
4.3或7 【解析】 由P是线段MN的中点,Q是线段NC的中点,得PN=12MN=12×10=5(cm),QN=12NC=12×4=2(cm).根据题意知,有两种情形.①当点C在线段MN上时,如图1,PQ=PN-QN=5-2=3(cm);②当点C在线段MN的延长线上时,如图2, PQ= PN+QN=5+2=7(cm).综上,线段PQ的长度是3 cm或7 cm.
?
5.如图,数轴上A,B两点表示的数分别为-2和6,数轴上的点C满足AC=BC,点D在线段AC的延长线上.若AD=32AC,则BD= ,点D表示的数为 .?
?
答案
5.2 4 【解析】 如图,因为A,B两点表示的数分别为-2和6,所以AB=6-(-2)=8,所以AC=BC=12AB=4,所以AD=32AC=6,所以BD=AB-AD=2.结合数轴知,点D表示的数为4.
?
6.如图,点C是线段AB上一点,点M,N,P分别是线段AC,BC,AB的中点.若AC=3,CP=1,则线段PN的长为 .?
答案
6.32 【解析】 因为AC=3,CP=1,所以AP=AC+CP=4.因为点P是线段AB的中点,所以AB=2AP=8,所以CB=AB-AC=5.因为点N是线段CB的中点,所以CN=12CB=52,所以PN=CN-CP=52-1=32.
?
7.如图,已知线段a,b,求作线段AB=3a-b,并写出作图步骤.
答案
7.【解析】 作射线AF;用圆规在射线AF上顺次截取AC=CD=DE=a;在线段AE上截取EB=b.则线段AB就是所求作的线段,如图所示.
8.[2019辽宁锦州期末]如图,线段AD=10 cm,B是AD上一动点,沿A→D→A以2 cm/s的速度往返运动1次,当B不与点D重合时,C是线段BD的中点,设点B运动时间为t(0≤t≤10)s.
(1)当t=2时,①AB= cm;②求线段CD的长度.?
(2)用含t的代数式表示运动过程中AB的长.
(3)在运动过程中,若AB的中点为E,则EC的长是否发生变化?若不变,求出EC的长;若发生变化,请说明理由.
答案
8.【解析】 (1)① 4
②因为AD=10 cm,AB=4 cm,
所以BD=10-4=6(cm).
因为C是线段BD的中点,
所以CD=12BD=12×6=3(cm).
(2)因为B是线段AD上一动点,沿A→D→A以2 cm/s的速度往返运动,
所以当0≤t≤5时,AB=2t cm;
当5(3)不变.理由如下:
因为AB的中点为E,C是线段BD的中点,
所以EC=12(AB+BD)=12AD=12×10=5(cm).
?
3 角
1.下面表示锐角∠ABC的是 ( )
答案
1.C
知识点1 角的定义和表示方法
2.在如图所示的图形中,可用∠AOB,∠1,∠O三种方法表示同一个角的是 ( )
答案
2.B
知识点1 角的定义和表示方法
3.如图,写出符合下列条件的角.(图中所有的角是指小于平角的角)
(1)写出能用一个大写字母表示的角;
(2)写出以点B为顶点的角;
(3)图中共有多少个角?
答案
3.【解析】 (1)能用一个大写字母表示的角有∠A,∠C.
(2)以点B为顶点的角有∠ABC,∠ABD,∠CBD.
(3)题图中共有7个角.
知识点1 角的定义和表示方法
4.如图,以O为顶点且小于180°的角有( )
A.6个
B.7个
C.8个
D.9个
答案
4.D 【解析】 以O为顶点且小于180°的角有∠AOC,∠AOD,∠AOE,∠COD,∠COE,∠COB,∠DOE,∠DOB,∠EOB,共9个.故选D.
知识点2 角的度量及换算
5.(1)8.76°= ° ' ″;?
(2)4°13'48″= °;?
(3)36 000″= '= °;?
(4)0.15°= '= ″.?
答案
5.(1)8 45 36;(2)4.23;(3)600 10;(4)9 540
知识点2 角的度量及换算
6.计算:
(1)[2020黑龙江齐齐哈尔铁锋区期末]50°24'×3;
(2)[2020吉林长春期末]20°18'+34°56'-12°34'.
答案
6.【解析】 (1)50°24'×3=50°×3+24'×3=151°12'.
(2)20°18'+34°56'-12°34'=54°74'-12°34'=42°40'.
知识点2 角的度量及换算
7.如图,一张地图上有A,B,C三地,C地在A地东南方向,若∠BAC=83°,则B地在A地的 ( )
A.南偏西38°方向
B.北偏东52°方向
C.南偏西52°方向
D.西南方向
答案
7.A 【解析】 如图,由题意得,∠CAD=45°,所以∠BAD= ∠BAC-∠CAD=38°,即B地在A地的南偏西38°方向.故选A.
知识点3 钟面上的角和方位角
在解决方位角问题时,一定要注意是以哪个位置为中心去描述方位
8.钟表在8:30时,时针与分针所成角的度数为 ,2:40时,时针与分针所成角的度数是 .?
答案
8.75° 160° 【解析】 钟面上有12个大格,60个小格,每个大格30°,每个小格6°,分针每分钟走6°,时针每分钟走0.5°.8:30时,时针与分针之间有2.5个大格,所以时针与分针所成角的度数为2.5×30°=75°,同理,2:40时,时针与分针所成角的度数是160°.
知识点3 钟面上的角和方位角
1.阅读下列语句:①在∠AOB的边OA的延长线上取一点P;②角的两边可长可短;③一条直线就是一个平角;④有公共点的两条射线组成的图形叫做角.其中错误的语句有 ( )
A.1个 B.2个 C.3个 D.4个
答案
1.D 【解析】 ①∠AOB的边OA是射线,不必延长,该语句错误;②角的两边是射线,无限长,该语句错误;③直线和平角是两个概念,平角是由处在同一直线上,但方向相反的两条射线构成的角,不能将直线和平角混为一谈,该语句错误;④有公共端点的两条射线组成的图形叫做角,该语句错误.故选D.
2.已知∠α=18°18',∠β=18.18°,∠γ=18.3°,下列结论正确的是 ( )
A.∠α=∠β B.∠α<∠β
C.∠α=∠γ D.∠β>∠γ
答案
2.C 【解析】 ∠α=18°18'=18.3°,所以∠α=∠γ>∠β,故C项正确.
3.[2020湖北武汉汉阳区期末]如图,某海域有三个小岛A,B,O,在小岛O处观测到小岛A在北偏东60°的方向上,小岛B在南偏东40°的方向上,则∠AOB的度数是 .?
答案
3.80° 【解析】 如图,由题意得∠AOC=60°,∠BOD=40°,所以∠AOB=180°-∠AOC-∠BOD=80°.
4.[2019广东佛山南海区期末]现代人常常受到颈椎不适的困扰,其症状包括:酸胀、隐痛、发紧、僵硬等,而将两臂向上抬,举到10点10分处,每天连续走200米,能有效缓解此症状;这里的10点10分处指的是时钟在10点10分时时针和分针的夹角,请你求出这个夹角的度数是 .?
答案
4.115° 【解析】 当时间为10点整时,时针、分针的夹角是60°.当时间为10点10分时,时针走了5°,分针正好走了60°,此时时针和分针的夹角是60°-5°+60°=115°.
5.魏老师去农贸市场买菜时发现,若把10千克的菜放在秤上,则指针盘上的指针转了180°,第二天魏老师请同学们回答以下两个问题:
(1)若把0.5千克的菜放在秤上,则指针转过 度;?
(2)若指针转了243°,则这些菜共有 千克.?
答案
5.(1)9;(2)13.5 【解析】 (1)由题意,可知把1千克的菜放在秤上,指针转过的度数为180°10=18°,所以如果把0.5千克的菜放在秤上,指针转过的度数为0.5×18°=9°;(2)因为243°÷18°=13.5,所以如果指针转了243°,这些菜共有13.5千克.
?
6.计算:
(1)32°19'+16°53'16″;
(2)72°35'÷2+18°33'×4.
答案
6.【解析】 (1)32°19'+16°53'16″
=32°+16°+19'+53'+16″
=48°72'16″
=49°12'16″.
(2)72°35'÷2+18°33'×4
=36°17'30″+74°12'
=110°29'30″.
7.如图,小明的地图上有A,B,C三地,地图被墨迹污染,C 地具体位置看不清楚了,但知道C地在A地的北偏东30°,在B地的南偏东45°,请你帮他确定C地的位置.
答案
7.【解析】 要确定C地的位置,只需画出以B为端点南偏东45°方向的射线和以A为端点北偏东30°方向的射线,如图所示,两射线的交点即C地的位置.
8.日常生活中,我们几乎每天都要看钟表,它的时针和分针如同兄弟俩在赛跑,其中蕴涵着丰富的数学知识.
(1)如图1,上午8:00这一时刻,时钟上分针与时针的夹角等于 ;?
(2)请在图2中画出8:20这一时刻时针和分针的大致位置,思考并回答:从上午8:00到8:20,时钟的分针转过的度数是 ,时钟的时针转过的度数是 ;?
(3)“元旦”这一天,小明上午八点整出门买东西,回到家中时发现还没到九点,但是时针与分针重合了,那么小明从离开家到回到家的时间为多少分钟?
答案
8.【解析】 (1)120°
(2)图略 120° 10°
因为分针每分钟转过6°,时针每分钟转过0.5°,所以上午8:00到8:20时分针转过的度数为120°,时针转过的度数为10°.
(3)设小明从离开家到回到家的时间为x分钟,
因为8点整时,时针与分针的夹角为120°,到家时,时针与分针重合,即分针比时针多走了240°,所以6x-0.5x=240,解得x=48011,
即小明从离开家到回到家的时间为48011 分钟.
?
钟面角是常见的一种角的问题,求钟面角首先要清楚时针和分针每分钟转过的度数,其次时针与分针的问题很多时候类似于追及问题.本题中时针与分针重合其实就是分针追上了时针,所以分针比时针多走了240°.
4 角的比较
1.用“叠合法”比较∠1与∠2的大小,正确的是( )
答案
1.D 【解析】 使用“叠合法”时,必须把两角叠合起来.此种方法一定要使两个角的顶点及一边重合,另一边落在重合的这两边的同侧,然后比较大小,所以D正确.故选D.
知识点1 角的比较
2.如图,在4×4的方格纸上,记∠ABD=α,∠DEF=β,∠CGH=γ,则 ( )
A.α<β<γ
B.β<α<γ
C.β<γ<α
D.α<γ<β
答案
2.C 【解析】 由题中图形可知,γ=90°,α>90°,β<90°,所以β<γ<α.故选C.
知识点1 角的比较
3.如图,求解下列问题:
(1)比较∠COD和∠COE的大小;
(2)借助三角尺,比较∠EOD和∠COD的大小;
(3)利用量角器,比较∠BOC和∠COD的大小.
答案
3.【分析】 (1)可用叠合法比较.∠COD和∠COE有一条公共边OC,而∠COD的另一条边OD在∠COE的内部,故∠COD<∠COE;(2)选择三角尺的一个锐角分别与这两个角比较大小;(3)通过度量容易得出结论.
【解析】 (1)由题图可以看出,∠COD<∠COE.
(2)用三角尺中30°的角分别和这两个角比较,可以发现∠EOD<30°,∠COD>30°,所以∠EOD<∠COD.
(3)通过度量可知∠BOC=20°,∠COD=70°,所以∠BOC<∠COD.
知识点1 角的比较
4.[2020安徽合肥期末]如图,∠AOC为直角,OC平分∠BOD,且∠AOB=34°,则∠AOD的度数为 ( )
A.120°
B.136°
C.146°
D.158°
答案
4.C 【解析】 由题意,得∠BOC=∠AOC-∠AOB=90°-34°=56°, 因为OC平分∠BOD,所以∠COD=∠BOC=56°,所以∠AOD=∠AOC+∠COD=90°+56°=146°.故选C.
知识点2 角的平分线
5.[2020广东深圳南山区期末]已知三条不同的射线OA,OB,OC,给出下列条件:①∠AOC=∠BOC;②∠AOB=2∠AOC;③∠AOC+∠COB=∠AOB;④∠BOC=12∠AOB.其中能确定OC平分∠AOB的有 ( )
A.1个 B.2个 C.3个 D.4个
?
答案
5.A 【解析】 易知①符合题意;②如图1,∠AOB=2∠AOC,但OC不平分∠AOB,故②不符合题意;③不确定∠AOC与∠COB的大小关系,故不能确定OC平分∠AOB,故③不符合题意;④如图2,∠BOC=12∠AOB,但OC不平分∠AOB,故④不符合题意.故选A.
?
知识点2 角的平分线
6.[2020辽宁锦州期末]把三角尺ABC与BDE按如图所示的方式拼在一起,其中A,B,D三点在同一直线上,BM为∠CBE的平分线,BN为∠DBE的平分线,则∠MBN的度数为 .?
答案
6.67.5° 【解析】 由题意知,∠ABC=45°,∠DBE=60°,∠ABD=180°,所以∠CBE=75°.因为BM为∠CBE的平分线,BN为∠DBE的平分线,所以∠MBE=37.5°,∠EBN=30°,所以∠MBN=∠MBE+∠EBN=67.5°.
知识点2 角的平分线
7.[2020安徽六安裕安区期末]如图,已知∠AOC=90°,∠COD比∠DOA大30°,OB是∠AOC的平分线,求∠BOD的度数.
答案
7.【解析】 因为∠COD比∠DOA大30°,所以∠COD=∠DOA+30°.
因为∠AOC=90°,所以∠COD+∠DOA=90°,
所以∠DOA+30°+∠DOA=90°,所以∠DOA=30°.
因为OB是∠AOC的平分线,
所以∠AOB=∠BOC=12∠AOC=45°,
所以∠BOD=∠AOB-∠DOA=45°-30°=15°.
?
知识点2 角的平分线
8.如图,∠AOB=90°,直线CD经过点O,∠BOD=110°.则∠AOC的度数为 ( )
A.30°
B.20°
C.15°
D.10°
答案
8.B 【解析】 因为∠COD是平角,∠BOD=110°,所以∠BOC=∠COD-∠BOD=180°-110°=70°.因为 ∠AOB=90°,所以 ∠AOC=∠AOB-∠BOC=90°-70°=20°.故选B.
知识点3 角的相关计算
9.[2020辽宁辽阳期末]如图,∠AOB=100°,∠BOC=30°,小明想过点O引一条射线OD,使∠AOD∶∠BOD=1∶3(∠AOD与∠BOD都小于平角),那么∠COD的度数是 ( )
A.45°
B.45°或105°
C.120°
D.45°或120°
答案
9.D 【解析】 当OD在∠AOB的内部时,由∠AOD∶∠BOD=1∶3,得∠AOD=100°4=25°,所以∠COD=∠AOB-∠BOC-∠AOD=100°-30°-25°=45°;当OD在∠AOB的外部时,由∠AOD∶∠BOD=1∶3,得∠AOD=100°2=50°,所以∠COD=∠BOD-∠BOC=150°-30°=120°.综上,∠COD的度数是45°或120°.故选D.
?
知识点3 角的相关计算
10.如图,已知OM是∠AOC的平分线,ON平分∠BOC.若∠AOC=120°,∠BOC=30°,则∠MON= °.?
答案
10.45 【解析】 因为OM是∠AOC的平分线,ON平分∠BOC,所以∠COM=12∠AOC=60°,∠CON=12∠BOC=15°,所以∠MON=∠COM-∠CON=60°-15°=45°.
?
知识点3 角的相关计算
1.[2019江苏苏州吴中区期末]如图,已知∠AOB=∠BOC=∠COD,下列结论错误的是 ( )?
A.OB,OC分别平分∠AOC,∠BOD
B.∠AOD=∠AOB+∠AOC
C.∠BOC=12∠AOD-∠AOB
D.∠COD=12(∠AOD-∠BOC)
?
答案
1.C 【解析】 不妨设∠AOB=∠BOC=∠COD=x°,则∠AOD=3x°,所以12∠AOD-∠AOB=32x°-x°=12x°,所以∠BOC≠ 12∠AOD-∠AOB,C项错误.故选C.
?
2.如图,直线AB,CD交于点O,∠AOE=90°,若∠AOC∶∠COE=4∶5,则∠AOD为 ( )
A.120°
B.130°
C.140°
D.150°
答案
2.C 【解析】 因为∠AOE=90°,所以∠AOC+∠COE=90°.因为∠AOC∶∠COE=4∶5,所以∠AOC=40°,所以∠AOD=180°-40°=140°.故选C.
3.如图,已知点O在直线AB上,∠COE=90°,OD平分∠AOE,∠COD=25°,则∠BOD的度数为 ( )
A.65°
B.100°
C.115°
D.130°
答案
3.C 【解析】 因为∠COE=90°,∠COD=25°,所以∠DOE=∠COE-∠COD=65°.因为OD平分∠AOE,所以∠AOD= ∠DOE=65°,所以∠BOD=180°-∠AOD=115°.故选C.
4.如图,OM,ON分别是∠BOC和∠AOC的平分线,∠AOB=84°.
(1)∠MON= ;?
(2)当OC在∠AOB内部绕点O转动时,∠MON的度数 改变.(填“会”或“不会”)?
答案
4.(1)42°;(2)不会 【解析】 (1)因为OM,ON分别是∠BOC和∠AOC的平分线,所以∠COM=12∠BOC,∠NOC= 12∠AOC, 又因为∠AOB=84°,所以∠MON=∠NOC+∠COM=12(∠AOC+∠BOC)=12×84°=42°;(2)由(1)知∠MON= 12∠AOB=12×84°=42°,是定值,与OC的位置无关.
?
5.如图,∠AOB=60°,OC是∠AOB的平分线,OC1是∠AOC的平分线,OC2是∠AOC1的平分线??OCn是∠AOCn-1的平分线,则∠AOCn的度数为 .?
答案
5.(12)n+1×60°(或(602????+1)°) 【解析】 由角平分线的定义可得∠AOC=12×60°=30°,∠AOC1=12×30°=14×60°= (12)2×60°= 15°, ∠AOC2=12×15°=18×60°=(12)3×60°=7.5°,?,∠AOCn=(12)n+1×60°=(602????+1)°.
?
6.[2020湖南娄底期末]如图,点O为直线AB上一点,∠BOC=80°,OE是∠BOC的平分线,2∠AOF=3∠COF.
(1)求∠AOF的度数;
(2)试说明OC平分∠EOF的理由.
答案
6.【解析】 (1)由题意,知∠AOC=180°-∠BOC=100°,
因为2∠AOF=3∠COF,所以∠AOF=35∠AOC=60°.
(2)因为∠AOF=60°,所以∠COF=40°,
又因为OE平分∠BOC,且∠BOC=80°,所以∠COE=40°,
所以∠COF=∠COE,所以OC平分∠EOF.
?
7.如图,点A,O,E在同一直线上,∠AOB=42°,∠COD=29°,OD平分∠COE.
(1)求∠AOD的度数;
(2)求∠COB的度数.
答案
7.【解析】 (1)因为∠COD=29°,OD平分∠COE,
所以∠DOE=∠COD=29°,
所以∠AOD=180°-∠DOE=180°-29°=151°.
(2)因为∠COD=29°,OD平分∠COE,
所以∠COE=2∠COD=58°,
因为∠AOB=42°,
所以∠COB=180°-∠AOB-∠COE=180°-42°-58°=80°.
8.如图,已知轮船A在灯塔P的北偏东30°的方向上,轮船B在灯塔P的南偏东70°的方向上.
(1)求从灯塔P看两轮船的视角(即∠APB)的度数;
(2)若轮船C在∠APB的平分线上,则轮船C在灯塔P的什么方向?
答案
8.【解析】 (1)由题意可知∠APN=30°,∠BPS=70°,
所以∠APB=180°-∠APN-∠BPS=80°.
(2)因为PC平分∠APB,且∠APB=80°,
所以∠APC=12∠APB=40°,
所以∠NPC=∠APN+∠APC=70°,
所以轮船C在灯塔P的北偏东70°的方向上.
?
9.[2019北京顺义区期末]阅读材料并回答问题:
数学课上,老师给出了如下问题:
如图1,∠AOB=120°,OC平分∠AOB,若∠COD=20°,请你补全图形,并求∠BOD的度数.
以下是小明的解答过程:
解:如图2,因为∠AOB=120°,OC平分∠AOB,
所以∠BOC= ∠AOB= .?
因为∠COD=20°,所以∠BOD= .?
(1)请你将小明的解答过程补充完整;
(2)你觉得小明的解答是否正确?如果不正确,指出错误之处并给出正确的解答过程.
答案
9.【解析】 (1)12 60° 40°
(2)不正确.
小明的解答忽略了当OD在∠BOC外部时的情形.
当OD在∠BOC外部时,如图,
由(1)可得,∠BOC=60°,所以∠BOD=∠BOC+∠COD=80°.
所以∠BOD的度数为40°或80°.
?
5 多边形和圆的
初步认识
1.如图所示的图形中,多边形的个数为 ( )
A.4
B.3
C.2
D.1
答案
1.B 【解析】 从左往右数:属于多边形的图形有第一个、第二个、第五个.注意,多边形是由3条或3条以上不在同一直线上的线段首尾顺次连接而成的封闭平面图形,故多边形中没有曲线.故选B.
知识点1 多边形
2.下列说法中,正确的个数是 ( )
①三角形是边数最少的多边形;
②由n条线段连接起来组成的图形叫多边形;
③n边形有n条边、n个顶点、2n个内角.
A.0 B.1
C.2 D.3
答案
2.B 【解析】 ②中说法不严密,理解多边形定义时需注意三点:一是线段“不在同一直线上”,二是必须是“封闭的平面图形”,三是“线段首尾顺次相连”.③中n边形有n个内角.故选B.
知识点1 多边形
3.把一个四边形截去一个角,剩下的多边形是( )
A.三角形
B.四边形
C.五边形
D.三角形或四边形或五边形
答案
3.D 【解析】 分三种情况,如图所示.故选D.
知识点1 多边形
4.[2019河南郑州期末]如果过一个多边形的一个顶点的对角线有七条,那么该多边形是 ( )
A.十边形 B.九边形
C.八边形 D.七边形
答案
4.A 【解析】 从n边形的一个顶点出发最多可以引(n-3)条对角线.由题意,得n-3=7,所以n=10,即这个多边形是十边形.故选A.
知识点2 多边形的对角线
5.[2020广东深圳龙华区期末]过一个多边形的一个顶点的所有对角线把多边形分成4个三角形,则这个多边形的边数为 ( )
A.3 B.4
C.5 D.6
答案
5.D 【解析】 从n边形的一个顶点出发引对角线,可以把多边形分成(n-2)个三角形.由题意,得n-2=4,所以n=6,即这个多边形的边数为6.故选D.
知识点2 多边形的对角线
6.一个多边形从一个顶点最多可以引8条对角线,则这个多边形共有 条对角线.?
答案
6.44 【解析】 设这个多边形的边数是n,由题意,得n-3=8,解得n=11,所以这个多边形对角线的条数为11×82=44.
?
知识点2 多边形的对角线
7.下列图形中,是正多边形的是 ( )
A.直角三角形
B.等腰三角形
C.长方形
D.正方形
答案
7.D 【解析】 正多边形的各边相等,各角也相等.正方形的四条边和四个角都相等.故选D.
知识点3 正多边形
8.下列说法中,正确的个数是 ( )
①由四条线段首尾顺次相连组成的封闭图形是四边形;
②各边都相等的多边形是正多边形;
③各角都相等的多边形一定是正多边形.
A.0 B.1
C.2 D.3
答案
8.A 【解析】 四条线段还需满足“在同一平面内”且“不在同一直线上”,故①不正确;各边相等、各角也相等的多边形是正多边形,两个条件必须同时具备,故②③不正确.故选A.
知识点3 正多边形
9.如图,木工师傅从边长为90 cm的正三角形木板ABC上锯出一个正六边形木板DEFGHK,那么正六边形木板的边长为 ( )
A.34 cm
B.32 cm
C.30 cm
D.28 cm
答案
9.C 【解析】 易知题图中各小三角形都是正三角形,且边长等于正六边形DEFGHK的边长,所以正六边形DEFGHK的边长是大正三角形ABC的边长的13,而大正三角形ABC的边长为90 cm,所以正六边形DEFGHK的边长是90÷3=30(cm).故选C.
?
知识点3 正多边形
10.某扇形占圆面积的15,则该扇形的圆心角为 ( )
A.72° B.60°
C.45° D.36°
?
答案
10.A 【解析】 15×360°=72°.故选A.
?
知识点4 圆及相关概念
11.一枚半径为r的硬币沿着直线滚动一圈,圆心经过的距离是 ( )
A.4πr B.2πr
C.πr D.2r
答案
11.B 【解析】 一枚半径为r的硬币沿着直线滚动一圈,圆心经过的距离就是圆的周长,即2πr.故选B.
知识点4 圆及相关概念
12.半径为3且圆心角为120°的扇形的面积为 .?
答案
12.3π 【解析】 半径为3的圆的面积为π×32=9π,所以圆心角为120°的扇形的面积为9π×120°360°=3π.
?
知识点4 圆及相关概念
扇形面积的计算方法
扇形面积的计算和圆的面积有关,即扇形的圆心角占圆周角的比例是多少,则扇形面积占圆的面积的比例就是多少.若扇形的圆心角为α,则扇形面积为S=????360°πr2.
?
13.[2020浙江温州期末]已知扇形的面积为3π cm2,扇形所在圆的半径为3 cm,则此扇形的圆心角为 °.?
答案
13.120 【解析】 半径为3 cm的圆的面积为π·32=9π(cm2),因为这个扇形的面积为3π cm2,所以这个扇形的圆心角为3π9π×360°=120°.
?
知识点4 圆及相关概念
1.[2019广东阳江江城区期中]若一个多边形共有14条对角线,则它是 ( )
A.六边形 B.七边形 C.八边形 D.九边形
答案
1.B 【解析】 n边形对角线的条数为????(?????3)2,将A,B,C,D中的多边形的边数依次代入,得6×(6?3)2=9,7×(7?3)2=14, 8×(8?3)2=20, 9×(9?3)2=27.故选B.
?
2.甲、乙两人各用一张正方形的纸片ABCD折出一个45°的角(如图所示),两人做法如下.
?
甲:将纸片ABCD沿对角线AC折叠,使点B落在点D上,则∠1=45°;
乙:将纸片ABCD沿AM,AN折叠,使点B、点D落在对角线AC上的同一点P上,则∠MAN=45°.
对于两人的做法,下列判断正确的是 ( )
A.甲、乙都对 B.甲对乙错
C.甲错乙对 D.甲、乙都错
答案
2.A 【解析】 由甲的做法知AC为∠DAB的平分线,所以∠1=12×90°=45°;由乙的做法知AM,AN分别为∠BAC, ∠DAC的平分线,所以∠MAP=12∠BAC,∠NAP=12∠DAC.因为∠BAC+∠DAC=∠DAB=90°,所以∠MAN=∠MAP+ ∠NAP=45°.故选A.
?
3.[2020四川巴中巴州区期末]若一个多边形截去一个角后变成十四边形,则原来的多边形的边数可能为( )
A.13或14 B.14或15
C.13,14或15 D.14,15或16
答案
3.C 【解析】 如图,n边形A1A2A3?An,若沿着直线A1A3截去一个角,则所得到的多边形比原来的多边形的边数少1;若沿着直线A1M截去一个角,则所得到的多边形与原来的多边形的边数相等;若沿着直线MN截去一个角,则所得到的多边形比原来的多边形的边数多1,因此将一个多边形截去一个角后,变成十四边形,则原来的多边形的边数可能为13,14或15.故选C.
4.[2019山东枣庄中考]如图,在边长为4的正方形ABCD中,以点B为圆心,AB为半径画弧,交BD于点E,则图中阴影部分的面积是(结果保留π) ( )
A.8-π
B.16-2π
C.8-2π
D.8-12π
?
答案
4.C 【解析】 由题意,知∠ABE=45°,所以扇形ABE的面积为45°360°π×42=2π.因为三角形ABD的面积为12×4×4=8,所以图中阴影部分的面积为8-2π.故选C.
?
5.如图,甲顺着大半圆从A地到B地,乙顺着两个小半圆从A地到B地,设甲、乙走过的路程分别为a,b,则 ( )
A.a=b
B.aC.a>b
D.无法确定
答案
5.A 【解析】 设大半圆的半径是R,则甲所走的路程是πR.设两个小半圆的半径分别是r1与r2,则r1+r2=R.故乙所走的路程是πr1+πr2=π(r1+r2)=πR,所以a=b.故选A.
6.[2020山东济南期末]已知一个时钟的分针长6 cm,则从9:00到9:26,分针扫过的面积为 cm2.?
7.某学校七年级的八个班进行足球比赛,比赛采用单循环制(即每两个班都进行一场比赛),则一共需要进行 场比赛.?
答案
6.785π 【解析】 因为时钟的分针走一小格转动6°,所以从9:00到9:26分针转动了26×6°=156°,所以分针扫过的面积为156°360°π×62=785π(cm2).
?
7.28 【解析】 参照多边形对角线条数的求法,比赛总场数即八边形的对角线条数与边数的和,所以一共需要进行比赛8×(8?3)2+8=28(场).
?
8.[2020浙江宁波北仑区期末]如图,将三个同样的正方形的一个顶点重合放置,那么∠1的度数为 .?
答案
8.20° 【解析】 如图,由题可知,∠BOD=90°-30°=60°,∠COE=90°-40°=50°,所以∠1=∠BOD+∠COE-∠BOE=60°+50°-90°=20°.
9.阅读材料:多边形上或内部的一点与多边形各顶点的连线,将多边形分割成若干个小三角形.图 1 给出了四边形的具体分割方法,分别将四边形分割成了 2 个、3个、4个小三角形,请你按照上述方法将图 2 中的六边形进行分割,并写出得到的小三角形的个数,试把这一结论推广至n边形.
答案
9.【解析】 如图所示.
?
分割法①可以把六边形分割成4个小三角形,把n边形分割成(n-2)个小三角形;
分割法②可以把六边形分割成5个小三角形,把n边形分割成(n-1)个小三角形;
分割法③可以把六边形分割成6个小三角形,把n边形分割成n个小三角形.
易错疑难集训
集训
1.(1)把23.29°转化为用度、分、秒表示的形式;
(2)把33°14'24″转化为用度表示的形式.
答案
1.【解析】 (1)23.29°=23°+0.29°=23°+0.29×60'=23°+17.4'=23°+17'+0.4×60″=23°+17'+24″=23°17'24″.
(2)33°14'24″=33°+14'+(24×160)'=33°+14'+0.4'=33°+14.4'=33°+(14.4×160)°=33°+0.24°=33.24°.
?
易错点1 度、分、秒转换时,误按十进制进行换算导致出错
本题容易把度、分、秒之间六十进制按十进制进行换算,容易得出错解:23.29°=23°2'9″,33°14'24″=34.64°.将度用度、分、秒表示时,先将度的小数部分化为分,再将分的小数部分化为秒;将度、分、秒用度表示时,先将秒化为分,再将分化为度.
2.已知平面上有公共端点的三条射线OA,OB,OC,若∠AOB=120°,∠BOC=60°,则∠AOC= .?
答案
2.60°或180° 【解析】 当射线OC在∠AOB内部时,因为∠AOB=120°,∠BOC=60°,所以∠AOC=∠AOB-∠BOC=120°-60°=60°;当射线OC在∠AOB外部时,因为∠AOB=120°,∠BOC=60°,所以∠AOC=∠AOB+∠BOC=120°+60°=180°.故∠AOC=60°或180°.
易错点2 不进行分类讨论导致漏解
3.如图,有两根木条AB和CD,其中AB的长为90,CD的长为140,在它们的中点处各有一个小圆孔M和N(圆孔直径忽略不计,M,N抽象成两个点),将它们的一端重合,放置在同一条直线上,求此时两根木条的小圆孔之间的距离.
易错点2 不进行分类讨论导致漏解
答案
3.【解析】 ①当B,C(或A,D)重合,且其余两端点在重合点两侧时,如图1所示,
?
?
MN=CN+BM=12CD+12AB=70+45=115;
②当A,C(或B,D)重合,且其余两端点在重合点同侧时,如图2所示,
?
?
MN=CN-AM=12CD-12AB=70-45=25.
故两根木条的小圆孔之间的距离为115或25.
?
易错点2 不进行分类讨论导致漏解
1.如图,已知数轴上有三点A,B,C,它们表示的数分别为a,b,c,且c-b=b-a,点C表示的数是20.
?
?
(1)若BC=30,求a,b的值;
(2)在(1)的条件下,动点P,Q分别从A,C两点同时出发向左运动,同时动点R从B点出发向右运动,点P,R,Q的速度分别为8个单位长度/秒、4个单位长度/秒、2个单位长度/秒,点M为线段PR的中点,点N为线段RQ的中点,在点R,Q相遇前,点P,Q,R运动多少秒时恰好满足 MR=4RN?
疑难点1 线段的动态问题
答案
1.【解析】 (1)因为BC=30,所以c-b=b-a=30,
因为点C表示的数是20,
所以点A表示的数为20-60=-40,点B表示的数为20-30=-10,
所以a的值为-40,b的值为-10.
(2)如图,由(1)可得AB=BC=30,
设在点R,Q相遇前,点P,Q,R运动x秒时恰好满足MR=4RN,则AP=8x,BR=4x,CQ=2x.
因为点M,N分别是线段PR,RQ的中点,
所以MR=12(8x+4x+30),RN=12(30-4x-2x),
所以当MR=4RN时,12(8x+4x+30)=4×12(30-4x-2x),
所以x=2.5,
所以在点R,Q相遇前,点P,Q,R运动2.5秒时恰好满足MR=4RN.
?
疑难点1 线段的动态问题
2.如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°,将一块透明的三角尺的直角顶点放在点O处,边OM在射线OB上,边ON在直线AB的下方.
(1)将图1中的三角尺绕点O逆时针旋转至如图2所示的位置,使边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数.
(2)将图1中的三角尺绕点O按每秒10°的速度逆时针旋转一周,在旋转过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为 (直接写出结果).?
(3)将图1中的三角尺绕点O逆时针旋转至如图3所示的位置,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的关系,并说明理由.
疑难点2 角平分线的几何表示及相关计算
答案
2.【解析】 (1)因为∠AOC=60°,所以∠BOC=120°,
因为OM平分∠BOC,所以∠COM=12∠BOC=60°,
所以∠CON=∠COM+∠MON=150°.
(2)6或24
如图1,当线段ON的反向延长线平分∠AOC时,∠COD=12∠AOC=30°,所以∠COM=90°-∠COD=60°,所以∠BOM=∠BOC-∠COM=60°,所以t=6010=6;如图2,当线段ON平分∠AOC时,∠CON=12∠AOC=30°,所以OM转过的度数为∠MON+∠CON+∠BOC=240°,t=24010=24.所以t的值为6或24.
?
疑难点2 角平分线的几何表示及相关计算
答案
(3)∠AOM-∠AON=30°.理由如下:
因为∠AOM+∠AON=∠MON=90°,∠AON+∠NOC=∠AOC=60°,
所以∠AOM=90°-∠AON,∠NOC=60°-∠AON,
所以∠AOM-∠NOC=90°-∠AON-(60°-∠AON)=30°.
疑难点2 角平分线的几何表示及相关计算
本题中考查的是动态几何和角平分线的相关知识,很多同学第(2)问会只写一种情况,要注意本题的要求是“直线ON恰好平分∠AOC”,这个时候线段ON可能在∠AOC内部,也可能在∠AOC外部.
数学·七年级上册·北师
1 线段、射线、直线
1.[2020广东佛山禅城区期末]手电筒射出的光线给我们的形象是 ( )
A.直线 B.射线 C.线段 D.折线
答案
1.B 【解析】 手电筒射出的光线可以抽象成射线.故选B.
知识点1 线段、射线、直线的概念
2.学校升国旗用的旗杆给我们的形象是 ( )
A.直线 B.射线
C.线段 D.折线
答案
2.C 【解析】 升国旗用的旗杆可以抽象成一条线段.故选C.
知识点1 线段、射线、直线的概念
3.下列说法中,正确的是 ( )
A.直线虽然没有端点,但长度是可以度量的
B.射线只有一个端点,但长度是可以度量的
C.线段虽然有两个端点,但长度却是可以变化的
D.只有线段的长度是可以度量的,直线、射线的长度不可以度量
答案
3.D
知识点1 线段、射线、直线的概念
4.下列各线段的表示方法中,正确的是 ( )
A.线段A B.线段ab
C.线段AB D.线段Ab
答案
4.C 【解析】 本题考查线段的表示方法,线段可以用一个小写字母表示,也可以用端点处的两个大写字母表示.故选C.
知识点2 线段、射线、直线的表示方法及画法
5.[2020天津和平区期末]下列语句中,正确的有 ( )
①直线MN与直线NM是同一条直线;
②射线AB与射线BA是同一条射线;
③线段PQ与线段QP是同一条线段;
④直线上一点把这条直线分成的两部分都是射线.
A.1个 B.2个 C.3个 D.4个
答案
5.C 【解析】 ②射线AB与射线BA,二者端点不同,不是同一条射线,故②不正确,正确的是①③④,共3个.故选C.
知识点2 线段、射线、直线的表示方法及画法
6.易错题[2019北京通州区期末]如图,点C为直线AB外一点,作射线AC,连接BC,则图中共含射线 条,其中能用字母表示出来的射线有 条.?
答案
6.6 3 【解析】 题图中以A为端点的射线有3条,以B为端点的射线有2条,以C为端点的射线有1条,共6条射线.其中能用字母表示出来的射线有射线AC、射线AB、射线BA,共3条.
知识点2 线段、射线、直线的表示方法及画法
7.如图,在平面内有A,B,C三点.
(1)画直线AC,线段BC,射线AB;
(2)在线段BC上任取一点D(不同于点B,C),连接线段AD;
(3)数数看,此时图中线段的条数.
答案
7.【解析】 (1)如图,直线AC,线段BC,射线AB即所求.
(2)如图,线段AD即所求.
(3)图中线段的条数为6.
知识点2 线段、射线、直线的表示方法及画法
8.[2020广东佛山期末]在墙壁上固定一根横放的木条,至少需要钉子的枚数是 ( )
A.1 B.2 C.3 D.4
答案
8.B 【解析】 根据两点确定一条直线,可知固定一根横放的木条,至少需要2枚钉子.故选B.
知识点3 直线的基本事实(两点确定一条直线)
9.下列现象中,可以用直线的基本事实“经过两点有且只有一条直线”来解释的有 ( )
①农民伯伯拉秧绳插秧;②园林工人栽一行树,先栽首尾的两棵树;③木匠师傅弹墨线.
A.0个 B.1个 C.2个 D.3个
答案
9.D
知识点3 直线的基本事实(两点确定一条直线)
10.过平面上四点中的任意两点画直线,甲说可画一条,乙说可画四条,丙说可画六条,丁说他们说得都不对,应该是一条,四条或六条,你觉得谁说得对?请画图来说明你的看法.
答案
10.【解析】 丁说得对.分三种情况:
(1)当四点共线时,可画一条直线,如图1;
(2)当四点中有三点共线时,可画四条直线,如图2;
(3)当四点中任意三点不共线时,可画六条直线,如图3.
知识点3 直线的基本事实(两点确定一条直线)
1.如图所示,下列说法不正确的是 ( )
A.直线AC经过点A
B.射线DE与直线AC有公共点
C.点F在直线AC上
D.线段AC与线段BD相交于点C
答案
1.D
2.[2020北京房山区期末]下列各项所给的线段、射线、直线能相交的是 ( )
答案
2.B
3.如图,点A,B,C在直线l上,则图中直线、线段、射线的条数分别为 ( )
A.3,3,3
B.1,2,3
C.1,3,6
D.3,2,6
答案
3.C 【解析】 题图中直线有1条;线段有AB,AC,BC,共3条;以A为端点的射线有2条,以B为端点的射线有2条,以C为端点的射线有2条,共6条射线.故选C.
4.观察下列图形,并阅读相关文字,则20条直线相交,交点个数最多是 ( )
A.190
B.210
C.380
D.420
答案
4.A 【解析】 由题图可以发现,2条直线相交最多有1个交点,3条直线相交最多有1+2=3个交点,4条直线相交最多有1+2+3=6个交点,所以20条直线相交最多有1+2+3+?+19=190个交点.故选A.
5.如图是射击比赛的图片,为了准确地击中靶心,运动员要进行瞄准,那么瞄准的数学原理是 .?
答案
5.两点确定一条直线
6.[2019江西抚州期中]如图,记以点A为端点的射线条数为x,以点D为其中一个端点的线段的条数为y,则x-y的值为 .?
答案
6.-2 【解析】 以点A为端点的射线有:射线AC,射线AB.所以x=2.以点D为其中一个端点的线段有:线段DA,线段DO,线段DB,线段DC.所以y=4,所以x-y=2-4=-2.
7.如图,数轴上的原点为O,点A表示3,点B表示-32.
(1)数轴是什么图形?
(2)数轴在原点O右边的部分(包括原点)是什么图形?怎样表示?
(3)射线OB上的点(除点O外)表示什么数?端点表示什么数?
(4)数轴上表示不小于-32且不大于3的部分是什么图形?怎样表示?
?
答案
7.【解析】 (1)数轴是直线.
(2)数轴在原点O右边的部分(包括原点)是射线,表示为射线OA.
(3)射线OB上的点(除点O外)表示负数,端点O表示0.
(4)数轴上表示不小于-32且不大于3的部分是线段,表示为线段BA或线段AB.
?
8.(1)如图1,直线上有2个点,则图中有 条可用图中字母表示的射线,有 条线段;?
(2)如图2,直线上有3个点,则图中有 条可用图中字母表示的射线,有 条线段;?
(3)如图3,直线上有n个点,则图中有 条可用图中字母表示的射线,有 条线段;?
(4)应用(3)中的发现,若火车的行驶路线上有20个车站,火车在这条线路上往返行车,需要印制多少种火车票?
答案
8.【解析】 (1)2 1
(2)4 3
(3)(2n-2) ????(?????1)2
以每个点为端点,左、右各有一条射线,所以有n个点就有2n条射线,而射线需用2个大写字母表示,所以最左边和最右边的射线无法表示,所以可以用题图中字母表示的射线有(2n-2)条.线段条数有如下规律:2个点时有1 条;3个点时有3条(3=1+2);4个点时有6条(6=1+2+3),所以n个点时有1+2+3+4+5+?+(n-1)=????(?????1)2(条).
(4)火车售票问题可以抽象成直线上有20个点时的线段条数问题.
因为火车往返行车,所以由(3)知有n(n-1)种火车票,
把n=20代入可知,需要印制20×(20-1)=380种火车票.
?
2 比较线段的长短
1.下列现象可用“两点之间线段最短”来解释的是 ( )
A.用两个钉子就可以把木条固定在墙上
B.正常情况下,射击时要保证瞄准的一只眼在准星和缺口确定的直线上,才能射中目标
C.从A地到B地架设电线,总是尽可能沿着线段AB架设
D.以上都不可以
答案
1.C 【解析】 A项和B项体现的是“两点确定一条直线”,C项体现的是“两点之间线段最短”.故选C.
知识点1 线段的基本事实(两点之间线段最短)
2.[2020江西南昌东湖区期末]如图,把三角形剪去一个角,所得四边形的周长比原三角形的周长小,能正确解释这一现象的数学知识是 ( )?
A.四边形周长小于三角形周长
B.两点确定一条直线
C.两点之间线段最短
D.经过一点有无数条直线
答案
2.C
知识点1 线段的基本事实(两点之间线段最短)
3.如图,设A,B,C,D为四个居民小区,现要建一个购物中心,试问把购物中心建在何处,才能使四个居民小区到购物中心的距离之和最小.请说明理由.
答案
3.【解析】 连接AD,BC 交于一点,该点即购物中心的位置.因为两点之间线段最短,到A,D距离之和最小的点在线段AD上,到B,C距离之和最小的点在线段BC上,所以到A,B,C,D距离之和最小的点就是线段AD和线段BC的交点.
知识点1 线段的基本事实(两点之间线段最短)
4.下列说法正确的是 ( )
A.过A,B两点的直线的长度是A,B两点间的距离
B.线段AB就是A,B两点间的距离
C.在连接A,B两点的所有线的长度中,最短的是A,B两点间的距离
D.乘高铁从上海到北京要走1 318千米,所以上海站与北京站之间的距离是1 318千米
答案
4.C 【解析】 两点间的距离指的是连接两点的线段的长度,故A项和B项错误,D项,乘高铁所走的路线不一定是线段,故D项错误.故选C.
知识点2 两点之间的距离
5.如果A,B,C三点在同一直线上,且线段AB=4 cm,BC=2 cm,那么A,C两点之间的距离是多少?
答案
5.【解析】 分两种情况.
(1)当点C在线段AB上时,如图1所示,AC=AB-BC,因为AB=4 cm,BC=2 cm,所以AC=4-2=2(cm);
?
(2)当点C在线段AB的延长线上时,如图2所示,AC=AB+BC,因为AB=4 cm,BC=2 cm,所以AC=4+2=6(cm).
知识点2 两点之间的距离
6.下列作图语句中,正确的是 ( )
A.作直线AB=3 cm
B.延长线段AB至点C,使 BC=AB
C.延长射线OA至点B,使AB=OA
D.作直线使之经过A,B,C三点
答案
6.B 【解析】 直线是向两方无限延伸的,所以不可度量,A项错误;射线OA是从端点O向A无限延伸的,所以只能反向延长射线OA,C项错误;当A,B,C三点不在同一条直线上时,无法作出一条直线能经过A,B,C三点,D项错误.故选B.
知识点3 利用尺规作图作线段
尺规作图语言表达的准确性
在尺规作图中,要求准确表达,由于直线和射线是无限延伸的,故不能出现延长直线或延长射线这样的描述,也不能作出有长度的直线和射线,同时要注意作图的合理性.
7.如图,已知线段a,b(a>b),按要求用尺规作图,并写出作图步骤.
(1)求作线段c,使c=a-b;
(2)求作线段d,使d=a+2b.
答案
7.【解析】 (1)作射线AD;用圆规在射线AD上截取AB=a;在线段AB上截取BC=b.则线段AC就是所求作的线段c,如图所示.
?
(2)作射线EI;用圆规在射线EI上顺次截取EF=a,FG=GH=b.则线段EH就是所求作的线段d,如图所示.
知识点3 利用尺规作图作线段
8.[2019北京海淀区期末]如图,用圆规比较两条线段AB和A'B'的长短,其中正确的是 ( )?
A.A'B'>AB
B.A'B'
D.无法比较
答案
8.B
知识点4 线段长短的比较
9.已知AB=6,下列四个选项能确定点C是线段AB的中点的是 ( )
A.BC=3 B.AC+BC=6
C.AC=BC=3 D.AB=2AC
答案
9.C 【解析】 当BC=3时,点C不一定在线段AB上,A项错误;当点C在线段AB上任意的位置时,AC+BC=6都成立,B项错误;当AC=BC=3时,点C一定是线段AB的中点,C项正确;当AB=2AC时,AC=3,但点C不一定在线段AB上,D项错误.故选C.
知识点5 线段的中点
10.[2020山东临沂河东区期末]如图,已知线段AB,C是线段AB上一点,M是AB的中点,N是AC的中点.
(1)若AB=8,AC=3.2,求线段MN的长;
(2)若BC=a,试用含a的式子表示线段MN的长.
知识点5 线段的中点
答案
10.【解析】 (1)因为AB=8,M是AB的中点,
所以AM=12AB=4.
因为AC=3.2,N是AC的中点,
所以AN=12AC=1.6,
所以MN=AM-AN=4-1.6=2.4.
(2)因为M是AB的中点,
所以AM=12AB.
因为N是AC的中点,
所以AN=12AC,
所以MN=AM-AN=12AB-12AC=12(AB-AC)=12BC=12a.
?
知识点5 线段的中点
1.如图,C,B是线段AD上的两点,若AB=CD,BC=2AC,则AC与CD的关系为 ( )
A.CD=2AC
B.CD=3AC
C.CD=4AC
D.不能确定
答案
1.B 【解析】 因为AB=CD,所以AB-BC=CD-BC,即AC=BD.因为BC=2AC,所以CD=3AC.故选B.
2.[2020湖北武汉汉阳区期末]如图,线段CD在线段AB上,且CD=3,若线段AB的长是正整数,则图中所有线段长的和可能是 ( )?
A.28
B.29
C.30
D.31
答案
2.C 【解析】 由题意,知所有线段长之和=AC+AD+AB+CD+CB+BD=AC+AC+3+AC+3+BD+3+3+BD+BD= 12+ 3(AC+ BD)=12+3(AB-3)=3AB+3=3(AB+1),因为AB是正整数,所以所有线段之和是3的倍数.故选C.
3.如图,线段AB上有两点C和D,其中AC∶BC=3∶4,AD∶DB=2∶5,且CD=2 cm,则线段AB的长为 ( )
A.12 cm
B.14 cm
C.16 cm
D.18 cm
答案
3.B 【解析】 设AC=3x,则BC=4x,所以AB=AC+BC=7x.因为AB=AD+DB,AD∶DB=2∶5,所以AD=2x,DB=5x,则CD=AC-AD=3x-2x=x=2 cm,所以AB=7×2=14(cm).故选B.
选择计算线段长度的方法的思路
计算线段的长度时,通常根据题中给定的条件,结合图形进行解答.一般考虑采用逐段计算法.若待求线段无法用已知线段的和或差表示出来,则考虑用整体计算法.若题中存在几条线段之间的比例关系时,则考虑运用方程思想求解.
4.已知线段MN=10 cm,点C是直线MN上一点,NC=4 cm,若P是线段MN的中点,Q是NC的中点,则线段PQ的长度是
cm.?
答案
4.3或7 【解析】 由P是线段MN的中点,Q是线段NC的中点,得PN=12MN=12×10=5(cm),QN=12NC=12×4=2(cm).根据题意知,有两种情形.①当点C在线段MN上时,如图1,PQ=PN-QN=5-2=3(cm);②当点C在线段MN的延长线上时,如图2, PQ= PN+QN=5+2=7(cm).综上,线段PQ的长度是3 cm或7 cm.
?
5.如图,数轴上A,B两点表示的数分别为-2和6,数轴上的点C满足AC=BC,点D在线段AC的延长线上.若AD=32AC,则BD= ,点D表示的数为 .?
?
答案
5.2 4 【解析】 如图,因为A,B两点表示的数分别为-2和6,所以AB=6-(-2)=8,所以AC=BC=12AB=4,所以AD=32AC=6,所以BD=AB-AD=2.结合数轴知,点D表示的数为4.
?
6.如图,点C是线段AB上一点,点M,N,P分别是线段AC,BC,AB的中点.若AC=3,CP=1,则线段PN的长为 .?
答案
6.32 【解析】 因为AC=3,CP=1,所以AP=AC+CP=4.因为点P是线段AB的中点,所以AB=2AP=8,所以CB=AB-AC=5.因为点N是线段CB的中点,所以CN=12CB=52,所以PN=CN-CP=52-1=32.
?
7.如图,已知线段a,b,求作线段AB=3a-b,并写出作图步骤.
答案
7.【解析】 作射线AF;用圆规在射线AF上顺次截取AC=CD=DE=a;在线段AE上截取EB=b.则线段AB就是所求作的线段,如图所示.
8.[2019辽宁锦州期末]如图,线段AD=10 cm,B是AD上一动点,沿A→D→A以2 cm/s的速度往返运动1次,当B不与点D重合时,C是线段BD的中点,设点B运动时间为t(0≤t≤10)s.
(1)当t=2时,①AB= cm;②求线段CD的长度.?
(2)用含t的代数式表示运动过程中AB的长.
(3)在运动过程中,若AB的中点为E,则EC的长是否发生变化?若不变,求出EC的长;若发生变化,请说明理由.
答案
8.【解析】 (1)① 4
②因为AD=10 cm,AB=4 cm,
所以BD=10-4=6(cm).
因为C是线段BD的中点,
所以CD=12BD=12×6=3(cm).
(2)因为B是线段AD上一动点,沿A→D→A以2 cm/s的速度往返运动,
所以当0≤t≤5时,AB=2t cm;
当5
因为AB的中点为E,C是线段BD的中点,
所以EC=12(AB+BD)=12AD=12×10=5(cm).
?
3 角
1.下面表示锐角∠ABC的是 ( )
答案
1.C
知识点1 角的定义和表示方法
2.在如图所示的图形中,可用∠AOB,∠1,∠O三种方法表示同一个角的是 ( )
答案
2.B
知识点1 角的定义和表示方法
3.如图,写出符合下列条件的角.(图中所有的角是指小于平角的角)
(1)写出能用一个大写字母表示的角;
(2)写出以点B为顶点的角;
(3)图中共有多少个角?
答案
3.【解析】 (1)能用一个大写字母表示的角有∠A,∠C.
(2)以点B为顶点的角有∠ABC,∠ABD,∠CBD.
(3)题图中共有7个角.
知识点1 角的定义和表示方法
4.如图,以O为顶点且小于180°的角有( )
A.6个
B.7个
C.8个
D.9个
答案
4.D 【解析】 以O为顶点且小于180°的角有∠AOC,∠AOD,∠AOE,∠COD,∠COE,∠COB,∠DOE,∠DOB,∠EOB,共9个.故选D.
知识点2 角的度量及换算
5.(1)8.76°= ° ' ″;?
(2)4°13'48″= °;?
(3)36 000″= '= °;?
(4)0.15°= '= ″.?
答案
5.(1)8 45 36;(2)4.23;(3)600 10;(4)9 540
知识点2 角的度量及换算
6.计算:
(1)[2020黑龙江齐齐哈尔铁锋区期末]50°24'×3;
(2)[2020吉林长春期末]20°18'+34°56'-12°34'.
答案
6.【解析】 (1)50°24'×3=50°×3+24'×3=151°12'.
(2)20°18'+34°56'-12°34'=54°74'-12°34'=42°40'.
知识点2 角的度量及换算
7.如图,一张地图上有A,B,C三地,C地在A地东南方向,若∠BAC=83°,则B地在A地的 ( )
A.南偏西38°方向
B.北偏东52°方向
C.南偏西52°方向
D.西南方向
答案
7.A 【解析】 如图,由题意得,∠CAD=45°,所以∠BAD= ∠BAC-∠CAD=38°,即B地在A地的南偏西38°方向.故选A.
知识点3 钟面上的角和方位角
在解决方位角问题时,一定要注意是以哪个位置为中心去描述方位
8.钟表在8:30时,时针与分针所成角的度数为 ,2:40时,时针与分针所成角的度数是 .?
答案
8.75° 160° 【解析】 钟面上有12个大格,60个小格,每个大格30°,每个小格6°,分针每分钟走6°,时针每分钟走0.5°.8:30时,时针与分针之间有2.5个大格,所以时针与分针所成角的度数为2.5×30°=75°,同理,2:40时,时针与分针所成角的度数是160°.
知识点3 钟面上的角和方位角
1.阅读下列语句:①在∠AOB的边OA的延长线上取一点P;②角的两边可长可短;③一条直线就是一个平角;④有公共点的两条射线组成的图形叫做角.其中错误的语句有 ( )
A.1个 B.2个 C.3个 D.4个
答案
1.D 【解析】 ①∠AOB的边OA是射线,不必延长,该语句错误;②角的两边是射线,无限长,该语句错误;③直线和平角是两个概念,平角是由处在同一直线上,但方向相反的两条射线构成的角,不能将直线和平角混为一谈,该语句错误;④有公共端点的两条射线组成的图形叫做角,该语句错误.故选D.
2.已知∠α=18°18',∠β=18.18°,∠γ=18.3°,下列结论正确的是 ( )
A.∠α=∠β B.∠α<∠β
C.∠α=∠γ D.∠β>∠γ
答案
2.C 【解析】 ∠α=18°18'=18.3°,所以∠α=∠γ>∠β,故C项正确.
3.[2020湖北武汉汉阳区期末]如图,某海域有三个小岛A,B,O,在小岛O处观测到小岛A在北偏东60°的方向上,小岛B在南偏东40°的方向上,则∠AOB的度数是 .?
答案
3.80° 【解析】 如图,由题意得∠AOC=60°,∠BOD=40°,所以∠AOB=180°-∠AOC-∠BOD=80°.
4.[2019广东佛山南海区期末]现代人常常受到颈椎不适的困扰,其症状包括:酸胀、隐痛、发紧、僵硬等,而将两臂向上抬,举到10点10分处,每天连续走200米,能有效缓解此症状;这里的10点10分处指的是时钟在10点10分时时针和分针的夹角,请你求出这个夹角的度数是 .?
答案
4.115° 【解析】 当时间为10点整时,时针、分针的夹角是60°.当时间为10点10分时,时针走了5°,分针正好走了60°,此时时针和分针的夹角是60°-5°+60°=115°.
5.魏老师去农贸市场买菜时发现,若把10千克的菜放在秤上,则指针盘上的指针转了180°,第二天魏老师请同学们回答以下两个问题:
(1)若把0.5千克的菜放在秤上,则指针转过 度;?
(2)若指针转了243°,则这些菜共有 千克.?
答案
5.(1)9;(2)13.5 【解析】 (1)由题意,可知把1千克的菜放在秤上,指针转过的度数为180°10=18°,所以如果把0.5千克的菜放在秤上,指针转过的度数为0.5×18°=9°;(2)因为243°÷18°=13.5,所以如果指针转了243°,这些菜共有13.5千克.
?
6.计算:
(1)32°19'+16°53'16″;
(2)72°35'÷2+18°33'×4.
答案
6.【解析】 (1)32°19'+16°53'16″
=32°+16°+19'+53'+16″
=48°72'16″
=49°12'16″.
(2)72°35'÷2+18°33'×4
=36°17'30″+74°12'
=110°29'30″.
7.如图,小明的地图上有A,B,C三地,地图被墨迹污染,C 地具体位置看不清楚了,但知道C地在A地的北偏东30°,在B地的南偏东45°,请你帮他确定C地的位置.
答案
7.【解析】 要确定C地的位置,只需画出以B为端点南偏东45°方向的射线和以A为端点北偏东30°方向的射线,如图所示,两射线的交点即C地的位置.
8.日常生活中,我们几乎每天都要看钟表,它的时针和分针如同兄弟俩在赛跑,其中蕴涵着丰富的数学知识.
(1)如图1,上午8:00这一时刻,时钟上分针与时针的夹角等于 ;?
(2)请在图2中画出8:20这一时刻时针和分针的大致位置,思考并回答:从上午8:00到8:20,时钟的分针转过的度数是 ,时钟的时针转过的度数是 ;?
(3)“元旦”这一天,小明上午八点整出门买东西,回到家中时发现还没到九点,但是时针与分针重合了,那么小明从离开家到回到家的时间为多少分钟?
答案
8.【解析】 (1)120°
(2)图略 120° 10°
因为分针每分钟转过6°,时针每分钟转过0.5°,所以上午8:00到8:20时分针转过的度数为120°,时针转过的度数为10°.
(3)设小明从离开家到回到家的时间为x分钟,
因为8点整时,时针与分针的夹角为120°,到家时,时针与分针重合,即分针比时针多走了240°,所以6x-0.5x=240,解得x=48011,
即小明从离开家到回到家的时间为48011 分钟.
?
钟面角是常见的一种角的问题,求钟面角首先要清楚时针和分针每分钟转过的度数,其次时针与分针的问题很多时候类似于追及问题.本题中时针与分针重合其实就是分针追上了时针,所以分针比时针多走了240°.
4 角的比较
1.用“叠合法”比较∠1与∠2的大小,正确的是( )
答案
1.D 【解析】 使用“叠合法”时,必须把两角叠合起来.此种方法一定要使两个角的顶点及一边重合,另一边落在重合的这两边的同侧,然后比较大小,所以D正确.故选D.
知识点1 角的比较
2.如图,在4×4的方格纸上,记∠ABD=α,∠DEF=β,∠CGH=γ,则 ( )
A.α<β<γ
B.β<α<γ
C.β<γ<α
D.α<γ<β
答案
2.C 【解析】 由题中图形可知,γ=90°,α>90°,β<90°,所以β<γ<α.故选C.
知识点1 角的比较
3.如图,求解下列问题:
(1)比较∠COD和∠COE的大小;
(2)借助三角尺,比较∠EOD和∠COD的大小;
(3)利用量角器,比较∠BOC和∠COD的大小.
答案
3.【分析】 (1)可用叠合法比较.∠COD和∠COE有一条公共边OC,而∠COD的另一条边OD在∠COE的内部,故∠COD<∠COE;(2)选择三角尺的一个锐角分别与这两个角比较大小;(3)通过度量容易得出结论.
【解析】 (1)由题图可以看出,∠COD<∠COE.
(2)用三角尺中30°的角分别和这两个角比较,可以发现∠EOD<30°,∠COD>30°,所以∠EOD<∠COD.
(3)通过度量可知∠BOC=20°,∠COD=70°,所以∠BOC<∠COD.
知识点1 角的比较
4.[2020安徽合肥期末]如图,∠AOC为直角,OC平分∠BOD,且∠AOB=34°,则∠AOD的度数为 ( )
A.120°
B.136°
C.146°
D.158°
答案
4.C 【解析】 由题意,得∠BOC=∠AOC-∠AOB=90°-34°=56°, 因为OC平分∠BOD,所以∠COD=∠BOC=56°,所以∠AOD=∠AOC+∠COD=90°+56°=146°.故选C.
知识点2 角的平分线
5.[2020广东深圳南山区期末]已知三条不同的射线OA,OB,OC,给出下列条件:①∠AOC=∠BOC;②∠AOB=2∠AOC;③∠AOC+∠COB=∠AOB;④∠BOC=12∠AOB.其中能确定OC平分∠AOB的有 ( )
A.1个 B.2个 C.3个 D.4个
?
答案
5.A 【解析】 易知①符合题意;②如图1,∠AOB=2∠AOC,但OC不平分∠AOB,故②不符合题意;③不确定∠AOC与∠COB的大小关系,故不能确定OC平分∠AOB,故③不符合题意;④如图2,∠BOC=12∠AOB,但OC不平分∠AOB,故④不符合题意.故选A.
?
知识点2 角的平分线
6.[2020辽宁锦州期末]把三角尺ABC与BDE按如图所示的方式拼在一起,其中A,B,D三点在同一直线上,BM为∠CBE的平分线,BN为∠DBE的平分线,则∠MBN的度数为 .?
答案
6.67.5° 【解析】 由题意知,∠ABC=45°,∠DBE=60°,∠ABD=180°,所以∠CBE=75°.因为BM为∠CBE的平分线,BN为∠DBE的平分线,所以∠MBE=37.5°,∠EBN=30°,所以∠MBN=∠MBE+∠EBN=67.5°.
知识点2 角的平分线
7.[2020安徽六安裕安区期末]如图,已知∠AOC=90°,∠COD比∠DOA大30°,OB是∠AOC的平分线,求∠BOD的度数.
答案
7.【解析】 因为∠COD比∠DOA大30°,所以∠COD=∠DOA+30°.
因为∠AOC=90°,所以∠COD+∠DOA=90°,
所以∠DOA+30°+∠DOA=90°,所以∠DOA=30°.
因为OB是∠AOC的平分线,
所以∠AOB=∠BOC=12∠AOC=45°,
所以∠BOD=∠AOB-∠DOA=45°-30°=15°.
?
知识点2 角的平分线
8.如图,∠AOB=90°,直线CD经过点O,∠BOD=110°.则∠AOC的度数为 ( )
A.30°
B.20°
C.15°
D.10°
答案
8.B 【解析】 因为∠COD是平角,∠BOD=110°,所以∠BOC=∠COD-∠BOD=180°-110°=70°.因为 ∠AOB=90°,所以 ∠AOC=∠AOB-∠BOC=90°-70°=20°.故选B.
知识点3 角的相关计算
9.[2020辽宁辽阳期末]如图,∠AOB=100°,∠BOC=30°,小明想过点O引一条射线OD,使∠AOD∶∠BOD=1∶3(∠AOD与∠BOD都小于平角),那么∠COD的度数是 ( )
A.45°
B.45°或105°
C.120°
D.45°或120°
答案
9.D 【解析】 当OD在∠AOB的内部时,由∠AOD∶∠BOD=1∶3,得∠AOD=100°4=25°,所以∠COD=∠AOB-∠BOC-∠AOD=100°-30°-25°=45°;当OD在∠AOB的外部时,由∠AOD∶∠BOD=1∶3,得∠AOD=100°2=50°,所以∠COD=∠BOD-∠BOC=150°-30°=120°.综上,∠COD的度数是45°或120°.故选D.
?
知识点3 角的相关计算
10.如图,已知OM是∠AOC的平分线,ON平分∠BOC.若∠AOC=120°,∠BOC=30°,则∠MON= °.?
答案
10.45 【解析】 因为OM是∠AOC的平分线,ON平分∠BOC,所以∠COM=12∠AOC=60°,∠CON=12∠BOC=15°,所以∠MON=∠COM-∠CON=60°-15°=45°.
?
知识点3 角的相关计算
1.[2019江苏苏州吴中区期末]如图,已知∠AOB=∠BOC=∠COD,下列结论错误的是 ( )?
A.OB,OC分别平分∠AOC,∠BOD
B.∠AOD=∠AOB+∠AOC
C.∠BOC=12∠AOD-∠AOB
D.∠COD=12(∠AOD-∠BOC)
?
答案
1.C 【解析】 不妨设∠AOB=∠BOC=∠COD=x°,则∠AOD=3x°,所以12∠AOD-∠AOB=32x°-x°=12x°,所以∠BOC≠ 12∠AOD-∠AOB,C项错误.故选C.
?
2.如图,直线AB,CD交于点O,∠AOE=90°,若∠AOC∶∠COE=4∶5,则∠AOD为 ( )
A.120°
B.130°
C.140°
D.150°
答案
2.C 【解析】 因为∠AOE=90°,所以∠AOC+∠COE=90°.因为∠AOC∶∠COE=4∶5,所以∠AOC=40°,所以∠AOD=180°-40°=140°.故选C.
3.如图,已知点O在直线AB上,∠COE=90°,OD平分∠AOE,∠COD=25°,则∠BOD的度数为 ( )
A.65°
B.100°
C.115°
D.130°
答案
3.C 【解析】 因为∠COE=90°,∠COD=25°,所以∠DOE=∠COE-∠COD=65°.因为OD平分∠AOE,所以∠AOD= ∠DOE=65°,所以∠BOD=180°-∠AOD=115°.故选C.
4.如图,OM,ON分别是∠BOC和∠AOC的平分线,∠AOB=84°.
(1)∠MON= ;?
(2)当OC在∠AOB内部绕点O转动时,∠MON的度数 改变.(填“会”或“不会”)?
答案
4.(1)42°;(2)不会 【解析】 (1)因为OM,ON分别是∠BOC和∠AOC的平分线,所以∠COM=12∠BOC,∠NOC= 12∠AOC, 又因为∠AOB=84°,所以∠MON=∠NOC+∠COM=12(∠AOC+∠BOC)=12×84°=42°;(2)由(1)知∠MON= 12∠AOB=12×84°=42°,是定值,与OC的位置无关.
?
5.如图,∠AOB=60°,OC是∠AOB的平分线,OC1是∠AOC的平分线,OC2是∠AOC1的平分线??OCn是∠AOCn-1的平分线,则∠AOCn的度数为 .?
答案
5.(12)n+1×60°(或(602????+1)°) 【解析】 由角平分线的定义可得∠AOC=12×60°=30°,∠AOC1=12×30°=14×60°= (12)2×60°= 15°, ∠AOC2=12×15°=18×60°=(12)3×60°=7.5°,?,∠AOCn=(12)n+1×60°=(602????+1)°.
?
6.[2020湖南娄底期末]如图,点O为直线AB上一点,∠BOC=80°,OE是∠BOC的平分线,2∠AOF=3∠COF.
(1)求∠AOF的度数;
(2)试说明OC平分∠EOF的理由.
答案
6.【解析】 (1)由题意,知∠AOC=180°-∠BOC=100°,
因为2∠AOF=3∠COF,所以∠AOF=35∠AOC=60°.
(2)因为∠AOF=60°,所以∠COF=40°,
又因为OE平分∠BOC,且∠BOC=80°,所以∠COE=40°,
所以∠COF=∠COE,所以OC平分∠EOF.
?
7.如图,点A,O,E在同一直线上,∠AOB=42°,∠COD=29°,OD平分∠COE.
(1)求∠AOD的度数;
(2)求∠COB的度数.
答案
7.【解析】 (1)因为∠COD=29°,OD平分∠COE,
所以∠DOE=∠COD=29°,
所以∠AOD=180°-∠DOE=180°-29°=151°.
(2)因为∠COD=29°,OD平分∠COE,
所以∠COE=2∠COD=58°,
因为∠AOB=42°,
所以∠COB=180°-∠AOB-∠COE=180°-42°-58°=80°.
8.如图,已知轮船A在灯塔P的北偏东30°的方向上,轮船B在灯塔P的南偏东70°的方向上.
(1)求从灯塔P看两轮船的视角(即∠APB)的度数;
(2)若轮船C在∠APB的平分线上,则轮船C在灯塔P的什么方向?
答案
8.【解析】 (1)由题意可知∠APN=30°,∠BPS=70°,
所以∠APB=180°-∠APN-∠BPS=80°.
(2)因为PC平分∠APB,且∠APB=80°,
所以∠APC=12∠APB=40°,
所以∠NPC=∠APN+∠APC=70°,
所以轮船C在灯塔P的北偏东70°的方向上.
?
9.[2019北京顺义区期末]阅读材料并回答问题:
数学课上,老师给出了如下问题:
如图1,∠AOB=120°,OC平分∠AOB,若∠COD=20°,请你补全图形,并求∠BOD的度数.
以下是小明的解答过程:
解:如图2,因为∠AOB=120°,OC平分∠AOB,
所以∠BOC= ∠AOB= .?
因为∠COD=20°,所以∠BOD= .?
(1)请你将小明的解答过程补充完整;
(2)你觉得小明的解答是否正确?如果不正确,指出错误之处并给出正确的解答过程.
答案
9.【解析】 (1)12 60° 40°
(2)不正确.
小明的解答忽略了当OD在∠BOC外部时的情形.
当OD在∠BOC外部时,如图,
由(1)可得,∠BOC=60°,所以∠BOD=∠BOC+∠COD=80°.
所以∠BOD的度数为40°或80°.
?
5 多边形和圆的
初步认识
1.如图所示的图形中,多边形的个数为 ( )
A.4
B.3
C.2
D.1
答案
1.B 【解析】 从左往右数:属于多边形的图形有第一个、第二个、第五个.注意,多边形是由3条或3条以上不在同一直线上的线段首尾顺次连接而成的封闭平面图形,故多边形中没有曲线.故选B.
知识点1 多边形
2.下列说法中,正确的个数是 ( )
①三角形是边数最少的多边形;
②由n条线段连接起来组成的图形叫多边形;
③n边形有n条边、n个顶点、2n个内角.
A.0 B.1
C.2 D.3
答案
2.B 【解析】 ②中说法不严密,理解多边形定义时需注意三点:一是线段“不在同一直线上”,二是必须是“封闭的平面图形”,三是“线段首尾顺次相连”.③中n边形有n个内角.故选B.
知识点1 多边形
3.把一个四边形截去一个角,剩下的多边形是( )
A.三角形
B.四边形
C.五边形
D.三角形或四边形或五边形
答案
3.D 【解析】 分三种情况,如图所示.故选D.
知识点1 多边形
4.[2019河南郑州期末]如果过一个多边形的一个顶点的对角线有七条,那么该多边形是 ( )
A.十边形 B.九边形
C.八边形 D.七边形
答案
4.A 【解析】 从n边形的一个顶点出发最多可以引(n-3)条对角线.由题意,得n-3=7,所以n=10,即这个多边形是十边形.故选A.
知识点2 多边形的对角线
5.[2020广东深圳龙华区期末]过一个多边形的一个顶点的所有对角线把多边形分成4个三角形,则这个多边形的边数为 ( )
A.3 B.4
C.5 D.6
答案
5.D 【解析】 从n边形的一个顶点出发引对角线,可以把多边形分成(n-2)个三角形.由题意,得n-2=4,所以n=6,即这个多边形的边数为6.故选D.
知识点2 多边形的对角线
6.一个多边形从一个顶点最多可以引8条对角线,则这个多边形共有 条对角线.?
答案
6.44 【解析】 设这个多边形的边数是n,由题意,得n-3=8,解得n=11,所以这个多边形对角线的条数为11×82=44.
?
知识点2 多边形的对角线
7.下列图形中,是正多边形的是 ( )
A.直角三角形
B.等腰三角形
C.长方形
D.正方形
答案
7.D 【解析】 正多边形的各边相等,各角也相等.正方形的四条边和四个角都相等.故选D.
知识点3 正多边形
8.下列说法中,正确的个数是 ( )
①由四条线段首尾顺次相连组成的封闭图形是四边形;
②各边都相等的多边形是正多边形;
③各角都相等的多边形一定是正多边形.
A.0 B.1
C.2 D.3
答案
8.A 【解析】 四条线段还需满足“在同一平面内”且“不在同一直线上”,故①不正确;各边相等、各角也相等的多边形是正多边形,两个条件必须同时具备,故②③不正确.故选A.
知识点3 正多边形
9.如图,木工师傅从边长为90 cm的正三角形木板ABC上锯出一个正六边形木板DEFGHK,那么正六边形木板的边长为 ( )
A.34 cm
B.32 cm
C.30 cm
D.28 cm
答案
9.C 【解析】 易知题图中各小三角形都是正三角形,且边长等于正六边形DEFGHK的边长,所以正六边形DEFGHK的边长是大正三角形ABC的边长的13,而大正三角形ABC的边长为90 cm,所以正六边形DEFGHK的边长是90÷3=30(cm).故选C.
?
知识点3 正多边形
10.某扇形占圆面积的15,则该扇形的圆心角为 ( )
A.72° B.60°
C.45° D.36°
?
答案
10.A 【解析】 15×360°=72°.故选A.
?
知识点4 圆及相关概念
11.一枚半径为r的硬币沿着直线滚动一圈,圆心经过的距离是 ( )
A.4πr B.2πr
C.πr D.2r
答案
11.B 【解析】 一枚半径为r的硬币沿着直线滚动一圈,圆心经过的距离就是圆的周长,即2πr.故选B.
知识点4 圆及相关概念
12.半径为3且圆心角为120°的扇形的面积为 .?
答案
12.3π 【解析】 半径为3的圆的面积为π×32=9π,所以圆心角为120°的扇形的面积为9π×120°360°=3π.
?
知识点4 圆及相关概念
扇形面积的计算方法
扇形面积的计算和圆的面积有关,即扇形的圆心角占圆周角的比例是多少,则扇形面积占圆的面积的比例就是多少.若扇形的圆心角为α,则扇形面积为S=????360°πr2.
?
13.[2020浙江温州期末]已知扇形的面积为3π cm2,扇形所在圆的半径为3 cm,则此扇形的圆心角为 °.?
答案
13.120 【解析】 半径为3 cm的圆的面积为π·32=9π(cm2),因为这个扇形的面积为3π cm2,所以这个扇形的圆心角为3π9π×360°=120°.
?
知识点4 圆及相关概念
1.[2019广东阳江江城区期中]若一个多边形共有14条对角线,则它是 ( )
A.六边形 B.七边形 C.八边形 D.九边形
答案
1.B 【解析】 n边形对角线的条数为????(?????3)2,将A,B,C,D中的多边形的边数依次代入,得6×(6?3)2=9,7×(7?3)2=14, 8×(8?3)2=20, 9×(9?3)2=27.故选B.
?
2.甲、乙两人各用一张正方形的纸片ABCD折出一个45°的角(如图所示),两人做法如下.
?
甲:将纸片ABCD沿对角线AC折叠,使点B落在点D上,则∠1=45°;
乙:将纸片ABCD沿AM,AN折叠,使点B、点D落在对角线AC上的同一点P上,则∠MAN=45°.
对于两人的做法,下列判断正确的是 ( )
A.甲、乙都对 B.甲对乙错
C.甲错乙对 D.甲、乙都错
答案
2.A 【解析】 由甲的做法知AC为∠DAB的平分线,所以∠1=12×90°=45°;由乙的做法知AM,AN分别为∠BAC, ∠DAC的平分线,所以∠MAP=12∠BAC,∠NAP=12∠DAC.因为∠BAC+∠DAC=∠DAB=90°,所以∠MAN=∠MAP+ ∠NAP=45°.故选A.
?
3.[2020四川巴中巴州区期末]若一个多边形截去一个角后变成十四边形,则原来的多边形的边数可能为( )
A.13或14 B.14或15
C.13,14或15 D.14,15或16
答案
3.C 【解析】 如图,n边形A1A2A3?An,若沿着直线A1A3截去一个角,则所得到的多边形比原来的多边形的边数少1;若沿着直线A1M截去一个角,则所得到的多边形与原来的多边形的边数相等;若沿着直线MN截去一个角,则所得到的多边形比原来的多边形的边数多1,因此将一个多边形截去一个角后,变成十四边形,则原来的多边形的边数可能为13,14或15.故选C.
4.[2019山东枣庄中考]如图,在边长为4的正方形ABCD中,以点B为圆心,AB为半径画弧,交BD于点E,则图中阴影部分的面积是(结果保留π) ( )
A.8-π
B.16-2π
C.8-2π
D.8-12π
?
答案
4.C 【解析】 由题意,知∠ABE=45°,所以扇形ABE的面积为45°360°π×42=2π.因为三角形ABD的面积为12×4×4=8,所以图中阴影部分的面积为8-2π.故选C.
?
5.如图,甲顺着大半圆从A地到B地,乙顺着两个小半圆从A地到B地,设甲、乙走过的路程分别为a,b,则 ( )
A.a=b
B.aC.a>b
D.无法确定
答案
5.A 【解析】 设大半圆的半径是R,则甲所走的路程是πR.设两个小半圆的半径分别是r1与r2,则r1+r2=R.故乙所走的路程是πr1+πr2=π(r1+r2)=πR,所以a=b.故选A.
6.[2020山东济南期末]已知一个时钟的分针长6 cm,则从9:00到9:26,分针扫过的面积为 cm2.?
7.某学校七年级的八个班进行足球比赛,比赛采用单循环制(即每两个班都进行一场比赛),则一共需要进行 场比赛.?
答案
6.785π 【解析】 因为时钟的分针走一小格转动6°,所以从9:00到9:26分针转动了26×6°=156°,所以分针扫过的面积为156°360°π×62=785π(cm2).
?
7.28 【解析】 参照多边形对角线条数的求法,比赛总场数即八边形的对角线条数与边数的和,所以一共需要进行比赛8×(8?3)2+8=28(场).
?
8.[2020浙江宁波北仑区期末]如图,将三个同样的正方形的一个顶点重合放置,那么∠1的度数为 .?
答案
8.20° 【解析】 如图,由题可知,∠BOD=90°-30°=60°,∠COE=90°-40°=50°,所以∠1=∠BOD+∠COE-∠BOE=60°+50°-90°=20°.
9.阅读材料:多边形上或内部的一点与多边形各顶点的连线,将多边形分割成若干个小三角形.图 1 给出了四边形的具体分割方法,分别将四边形分割成了 2 个、3个、4个小三角形,请你按照上述方法将图 2 中的六边形进行分割,并写出得到的小三角形的个数,试把这一结论推广至n边形.
答案
9.【解析】 如图所示.
?
分割法①可以把六边形分割成4个小三角形,把n边形分割成(n-2)个小三角形;
分割法②可以把六边形分割成5个小三角形,把n边形分割成(n-1)个小三角形;
分割法③可以把六边形分割成6个小三角形,把n边形分割成n个小三角形.
易错疑难集训
集训
1.(1)把23.29°转化为用度、分、秒表示的形式;
(2)把33°14'24″转化为用度表示的形式.
答案
1.【解析】 (1)23.29°=23°+0.29°=23°+0.29×60'=23°+17.4'=23°+17'+0.4×60″=23°+17'+24″=23°17'24″.
(2)33°14'24″=33°+14'+(24×160)'=33°+14'+0.4'=33°+14.4'=33°+(14.4×160)°=33°+0.24°=33.24°.
?
易错点1 度、分、秒转换时,误按十进制进行换算导致出错
本题容易把度、分、秒之间六十进制按十进制进行换算,容易得出错解:23.29°=23°2'9″,33°14'24″=34.64°.将度用度、分、秒表示时,先将度的小数部分化为分,再将分的小数部分化为秒;将度、分、秒用度表示时,先将秒化为分,再将分化为度.
2.已知平面上有公共端点的三条射线OA,OB,OC,若∠AOB=120°,∠BOC=60°,则∠AOC= .?
答案
2.60°或180° 【解析】 当射线OC在∠AOB内部时,因为∠AOB=120°,∠BOC=60°,所以∠AOC=∠AOB-∠BOC=120°-60°=60°;当射线OC在∠AOB外部时,因为∠AOB=120°,∠BOC=60°,所以∠AOC=∠AOB+∠BOC=120°+60°=180°.故∠AOC=60°或180°.
易错点2 不进行分类讨论导致漏解
3.如图,有两根木条AB和CD,其中AB的长为90,CD的长为140,在它们的中点处各有一个小圆孔M和N(圆孔直径忽略不计,M,N抽象成两个点),将它们的一端重合,放置在同一条直线上,求此时两根木条的小圆孔之间的距离.
易错点2 不进行分类讨论导致漏解
答案
3.【解析】 ①当B,C(或A,D)重合,且其余两端点在重合点两侧时,如图1所示,
?
?
MN=CN+BM=12CD+12AB=70+45=115;
②当A,C(或B,D)重合,且其余两端点在重合点同侧时,如图2所示,
?
?
MN=CN-AM=12CD-12AB=70-45=25.
故两根木条的小圆孔之间的距离为115或25.
?
易错点2 不进行分类讨论导致漏解
1.如图,已知数轴上有三点A,B,C,它们表示的数分别为a,b,c,且c-b=b-a,点C表示的数是20.
?
?
(1)若BC=30,求a,b的值;
(2)在(1)的条件下,动点P,Q分别从A,C两点同时出发向左运动,同时动点R从B点出发向右运动,点P,R,Q的速度分别为8个单位长度/秒、4个单位长度/秒、2个单位长度/秒,点M为线段PR的中点,点N为线段RQ的中点,在点R,Q相遇前,点P,Q,R运动多少秒时恰好满足 MR=4RN?
疑难点1 线段的动态问题
答案
1.【解析】 (1)因为BC=30,所以c-b=b-a=30,
因为点C表示的数是20,
所以点A表示的数为20-60=-40,点B表示的数为20-30=-10,
所以a的值为-40,b的值为-10.
(2)如图,由(1)可得AB=BC=30,
设在点R,Q相遇前,点P,Q,R运动x秒时恰好满足MR=4RN,则AP=8x,BR=4x,CQ=2x.
因为点M,N分别是线段PR,RQ的中点,
所以MR=12(8x+4x+30),RN=12(30-4x-2x),
所以当MR=4RN时,12(8x+4x+30)=4×12(30-4x-2x),
所以x=2.5,
所以在点R,Q相遇前,点P,Q,R运动2.5秒时恰好满足MR=4RN.
?
疑难点1 线段的动态问题
2.如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°,将一块透明的三角尺的直角顶点放在点O处,边OM在射线OB上,边ON在直线AB的下方.
(1)将图1中的三角尺绕点O逆时针旋转至如图2所示的位置,使边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数.
(2)将图1中的三角尺绕点O按每秒10°的速度逆时针旋转一周,在旋转过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为 (直接写出结果).?
(3)将图1中的三角尺绕点O逆时针旋转至如图3所示的位置,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的关系,并说明理由.
疑难点2 角平分线的几何表示及相关计算
答案
2.【解析】 (1)因为∠AOC=60°,所以∠BOC=120°,
因为OM平分∠BOC,所以∠COM=12∠BOC=60°,
所以∠CON=∠COM+∠MON=150°.
(2)6或24
如图1,当线段ON的反向延长线平分∠AOC时,∠COD=12∠AOC=30°,所以∠COM=90°-∠COD=60°,所以∠BOM=∠BOC-∠COM=60°,所以t=6010=6;如图2,当线段ON平分∠AOC时,∠CON=12∠AOC=30°,所以OM转过的度数为∠MON+∠CON+∠BOC=240°,t=24010=24.所以t的值为6或24.
?
疑难点2 角平分线的几何表示及相关计算
答案
(3)∠AOM-∠AON=30°.理由如下:
因为∠AOM+∠AON=∠MON=90°,∠AON+∠NOC=∠AOC=60°,
所以∠AOM=90°-∠AON,∠NOC=60°-∠AON,
所以∠AOM-∠NOC=90°-∠AON-(60°-∠AON)=30°.
疑难点2 角平分线的几何表示及相关计算
本题中考查的是动态几何和角平分线的相关知识,很多同学第(2)问会只写一种情况,要注意本题的要求是“直线ON恰好平分∠AOC”,这个时候线段ON可能在∠AOC内部,也可能在∠AOC外部.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
