功率(授课用)
图片预览







文档简介
(共29张PPT)
《 功率 》
一、复习提问:
1.功的公式?
W=Fl cosα
2.正、负功的条件及意义 ?
1.条件:(1) 正功:0≤α<90°
2.意义: (1)正功、动力、推动作用 ;
(2) 负功: 90°<α≤180°
(2)负功、阻力、阻碍作用
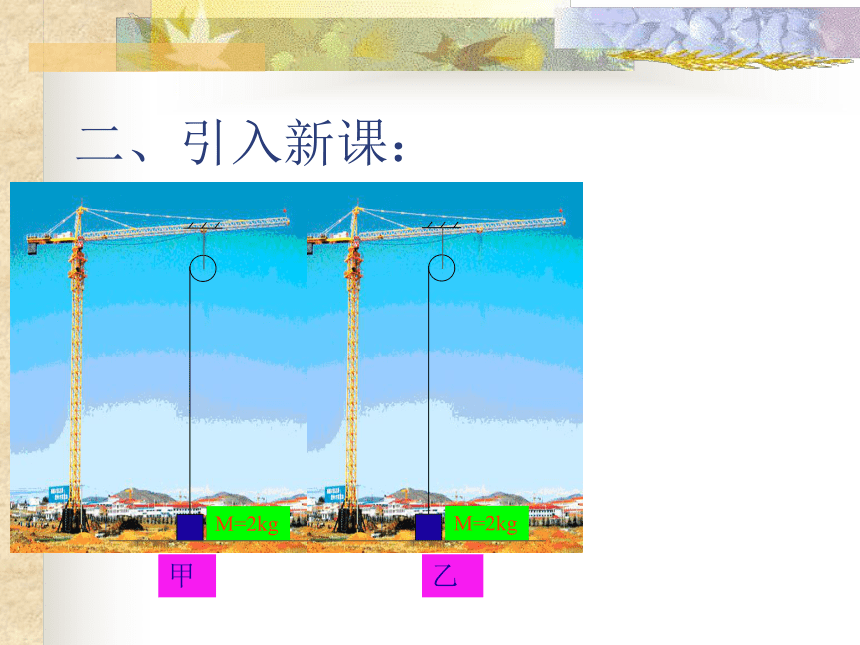
二、引入新课:
M=2kg
M=2kg
甲
乙
M=2kg
M=2kg
甲
乙
M=2kg
M=2kg
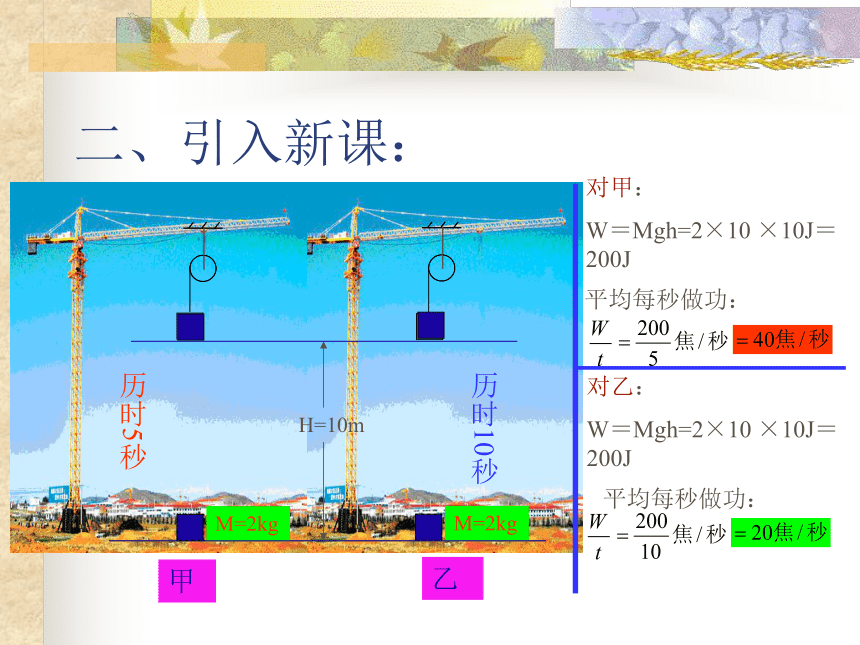
H=10m
历时5秒
历时10秒
二、引入新课:
对甲:
W=Mgh=2×10 ×10J=200J
对乙:
W=Mgh=2×10 ×10J=200J
平均每秒做功:
平均每秒做功:
三、讲解新课:
<一>功率:
3.单位:焦/秒(瓦特)简称“瓦”,符号:W
1瓦=1焦/秒。
技术上:千瓦, 1千瓦=1000瓦
2.定义式:P=
1.定义:功跟完成这些功所用时间 的比值叫做功率。
(或单位时间内完成的功)
功
时间
5.标量:功率是标量。
注:功率与的功的区别与联系:
区别:功是力对位移的积累。(无时间概念); 功率表示做功的快慢,与时间有关。
联系:功率是单位时间内完成的功。
4.物理意义:表示力做功的快慢。
P=
W=Fl cosα
练习题
1、关于功率,下列说法中正确的是( )
A、功率是说明做功多少的物理量
B、功率是说明力做功快慢的物理量
C、做功时间越长,功率一定小
D、力做功越多,功率一定大
B
<二>功率与速度的关系:
1、用F表示沿位移方向的力,
则W=Fl,
又:P =
∴P=
又∵ v=
∴P=Fv ·········(1)
结论:功率等于力和物体运动速率的乘积。
F
F
t
l
注: P=Fv ·········(1)
(1)式中F指的是v方向上的力。
若F与v互成角度α ,
(2)公式给出P、F、v三者相互制 约的关系。
F1
F2
P=Fvcosα (α为F、v夹角)
F
α
v
则有: PF=PF1=F1V, 而F1=Fcos α
则,公式变为:
F
l
<三>平均功率和瞬时功率 :
1、平均功率:
注:平均功率:对应一段时间或一个过程;
瞬时功率:对应一个时刻或一个位置。
2、瞬时功率:
P=Fv
代入瞬时速度,即得瞬时功率。
表示在一段时间内力对物体做功的平均快慢.
计算:
表示在某一时刻力对物体做功的快慢.
计算:
东风雪铁龙牌
<四>、几个常识性的概念:
1、机车功率:指牵引力功率,并非合力功率。
2、额定功率P额:指机器可以较长时间工作时输出的功率,即铭牌上的标称值。
3、实际功率P实:是指机器工作时实际输出功率。
故有:P实≤P额。
注:对一切机车,车辆设计时规定了正常行驶时最大功率,即额定功率(铭牌上标明),发动机工作时的实际功率,可以小于额定功率但不能长时间超过。
P=F v
功率与速度
思考:
(1)当功率p一定时,牵引力F和v之间关系如何
(2)当速度v一定时,牵引力F和P之间关系如何
(3)当牵引力F一定时,功率P和速度V之间有什么关系
F与v成反比
P与F成正比
P与v成正比
P=F v
发动机的实际功率
发动机的牵引力
机车的瞬时速度
思考:
(1)为什么机动车上坡时速度要比在平地上行驶的速度小得多呢?
分析:
根据P=Fv
P一定时,上坡时 需要的F ∴v
例1:
某型号汽车发动机的额定功率为60kw,在水平路面上行驶时受到的阻力是1500N,求:(1)发动机在额定功率下汽车匀速行驶的速度。 (2)在同样的阻力下,如果行驶速度只有15m/s,发动机输出的实际功率是多少?
分析:
解:(1)匀速行驶时,F=f=1500N。
由P=Fv=fv,得:
v= = 米/秒=40米/秒。
(2)以v1=15m/s匀速行驶时,
P实=Fv1=fv1=1500×15W=22500W=22.5kW
F
f
v
匀速行驶
根据P=Fv
已知P,需要求出F
汽车由静止启动,运动的情况有两种:
1. 以额定功率P额启动
2. 在恒定的牵引力F作用下启动
关于汽车的启动问题
汽车以恒定功率启动
F牵
F阻
mg
FN
类型1:机车以恒定功率 P 启动
专题:机车启动问题
P=F v
发动机的实际功率
发动机的牵引力
机车的瞬时速度
当F=F阻时,
a=0 ,v达到最大
保持
vm
匀速
v
F=
v
P
a=
m
F-F阻
↑
→
↓
↑
→
→
↓
↓
vm=
F阻
P
加速度逐渐减小的变加速直线运动
匀速直线运动
(功率P 恒定)
t1时刻:
0~t1:
t1后:
汽车做加速度越来越小的变加速直线运动。
F牵=F阻, a=0, 速度达最大为
汽车以速度vm做匀速直线运动。
0
t1
t
vm
v
v- t 图:
类型2:机车以恒定加速度 a 启动
当F= F阻时,
a=0 ,v达到最大
保持
vm
匀速
F=
v
P额
a=
m
F-F阻
↑
→
↓
v
↑
↓
→
→
↓
vm=
F阻
P额
加速度逐渐减小的变加速直线运动
匀速直线运动
a=
m
F-F阻
→
→
→
→
F
→
v
↑
P=F v
↑
↑
→
当P= P额时,保持P额继续加速
匀加速直线运动
机车以恒定加速度启动的v- t 图
先做匀加速直线运动,再做加速度逐渐减小的变加速直线运动,最终以速度 做匀速直线运动。
v
t
0
vm=
F阻
P额
vm
例2:
质量为m的物体在竖直向上的拉力作用下以加速度a由静止开始运动,当物体上升h高度的过程中,拉力的平均功率为多少?
F
h
a
mg
分析:
求
-
P
W=Fh
求F
牛顿第二定律
求
-
P
牛顿第二定律
求F
求末速度v
思路1
思路2
例2:
质量为m的物体在竖直向上的拉力作用下以加速度a由静止开始运动,当物体上升h高度的过程中,拉力的平均功率为多少?
F
h
a
mg
法1:
解:由牛顿第二定律:
F-mg=ma
∴ F=mg+ma= m(g+a)
W=Fh= m(g+a)h
又:h= 得:
∴ =
法2:
解:由牛顿第二定律:
F-mg=ma
∴ F=mg+ma= m(g+a)
由 得:
∴
∴ =
例3:
质量为m的物体从倾角为α的光滑斜面顶端由静止滑下,滑到斜面底端时的速度为v,求:重力的瞬时功率为多少?
V
α
mg
F1
F2
α
V
mg
法1:
解:P=mgVcos(90°-α)
=mgvsin α
法2:
解:将mg分解为沿速度方向和垂直于速度方向两个分力: F1=mg sin α
P= F1 V= mg vsin α
四、小结:
1、功率概念(与功区别联系)
(2)计算式: P=Fv
P=Fvcosα
(1)定义式:P=
(3)单位:瓦特(W)
2、平均功率和瞬时功率:
(2)瞬时功率
P=Fv
(1)平均功率:
P=
P=F
P实≤P额
3、额定功率P额和实际功率P实
4、P、F、v相互制约的关系。
2. 质量为0.2 kg的小球从高处自由下落,取g=10m/s2,则下落第三秒末重力做功的瞬时功率为________W,前三秒内重力做功的平均功率为________W。
1. 关于功率以下说法中正确的是 ( )
A.据 P=W/t可知,机器做功越多,其功率就越大
B.据 P=Fv可知,汽车牵引力一定与速度成反比
C.据 P=W/t可知,只要知道时间t内机器所做的功,就可以求得这段时间内任一时刻机器做功的功率
D.根据 P=Fv可知,发动机功率一定时,交通工具的牵引力与运动速度成反比
六、作业:
课后1、2题
创新设计
《 功率 》
一、复习提问:
1.功的公式?
W=Fl cosα
2.正、负功的条件及意义 ?
1.条件:(1) 正功:0≤α<90°
2.意义: (1)正功、动力、推动作用 ;
(2) 负功: 90°<α≤180°
(2)负功、阻力、阻碍作用
二、引入新课:
M=2kg
M=2kg
甲
乙
M=2kg
M=2kg
甲
乙
M=2kg
M=2kg
H=10m
历时5秒
历时10秒
二、引入新课:
对甲:
W=Mgh=2×10 ×10J=200J
对乙:
W=Mgh=2×10 ×10J=200J
平均每秒做功:
平均每秒做功:
三、讲解新课:
<一>功率:
3.单位:焦/秒(瓦特)简称“瓦”,符号:W
1瓦=1焦/秒。
技术上:千瓦, 1千瓦=1000瓦
2.定义式:P=
1.定义:功跟完成这些功所用时间 的比值叫做功率。
(或单位时间内完成的功)
功
时间
5.标量:功率是标量。
注:功率与的功的区别与联系:
区别:功是力对位移的积累。(无时间概念); 功率表示做功的快慢,与时间有关。
联系:功率是单位时间内完成的功。
4.物理意义:表示力做功的快慢。
P=
W=Fl cosα
练习题
1、关于功率,下列说法中正确的是( )
A、功率是说明做功多少的物理量
B、功率是说明力做功快慢的物理量
C、做功时间越长,功率一定小
D、力做功越多,功率一定大
B
<二>功率与速度的关系:
1、用F表示沿位移方向的力,
则W=Fl,
又:P =
∴P=
又∵ v=
∴P=Fv ·········(1)
结论:功率等于力和物体运动速率的乘积。
F
F
t
l
注: P=Fv ·········(1)
(1)式中F指的是v方向上的力。
若F与v互成角度α ,
(2)公式给出P、F、v三者相互制 约的关系。
F1
F2
P=Fvcosα (α为F、v夹角)
F
α
v
则有: PF=PF1=F1V, 而F1=Fcos α
则,公式变为:
F
l
<三>平均功率和瞬时功率 :
1、平均功率:
注:平均功率:对应一段时间或一个过程;
瞬时功率:对应一个时刻或一个位置。
2、瞬时功率:
P=Fv
代入瞬时速度,即得瞬时功率。
表示在一段时间内力对物体做功的平均快慢.
计算:
表示在某一时刻力对物体做功的快慢.
计算:
东风雪铁龙牌
<四>、几个常识性的概念:
1、机车功率:指牵引力功率,并非合力功率。
2、额定功率P额:指机器可以较长时间工作时输出的功率,即铭牌上的标称值。
3、实际功率P实:是指机器工作时实际输出功率。
故有:P实≤P额。
注:对一切机车,车辆设计时规定了正常行驶时最大功率,即额定功率(铭牌上标明),发动机工作时的实际功率,可以小于额定功率但不能长时间超过。
P=F v
功率与速度
思考:
(1)当功率p一定时,牵引力F和v之间关系如何
(2)当速度v一定时,牵引力F和P之间关系如何
(3)当牵引力F一定时,功率P和速度V之间有什么关系
F与v成反比
P与F成正比
P与v成正比
P=F v
发动机的实际功率
发动机的牵引力
机车的瞬时速度
思考:
(1)为什么机动车上坡时速度要比在平地上行驶的速度小得多呢?
分析:
根据P=Fv
P一定时,上坡时 需要的F ∴v
例1:
某型号汽车发动机的额定功率为60kw,在水平路面上行驶时受到的阻力是1500N,求:(1)发动机在额定功率下汽车匀速行驶的速度。 (2)在同样的阻力下,如果行驶速度只有15m/s,发动机输出的实际功率是多少?
分析:
解:(1)匀速行驶时,F=f=1500N。
由P=Fv=fv,得:
v= = 米/秒=40米/秒。
(2)以v1=15m/s匀速行驶时,
P实=Fv1=fv1=1500×15W=22500W=22.5kW
F
f
v
匀速行驶
根据P=Fv
已知P,需要求出F
汽车由静止启动,运动的情况有两种:
1. 以额定功率P额启动
2. 在恒定的牵引力F作用下启动
关于汽车的启动问题
汽车以恒定功率启动
F牵
F阻
mg
FN
类型1:机车以恒定功率 P 启动
专题:机车启动问题
P=F v
发动机的实际功率
发动机的牵引力
机车的瞬时速度
当F=F阻时,
a=0 ,v达到最大
保持
vm
匀速
v
F=
v
P
a=
m
F-F阻
↑
→
↓
↑
→
→
↓
↓
vm=
F阻
P
加速度逐渐减小的变加速直线运动
匀速直线运动
(功率P 恒定)
t1时刻:
0~t1:
t1后:
汽车做加速度越来越小的变加速直线运动。
F牵=F阻, a=0, 速度达最大为
汽车以速度vm做匀速直线运动。
0
t1
t
vm
v
v- t 图:
类型2:机车以恒定加速度 a 启动
当F= F阻时,
a=0 ,v达到最大
保持
vm
匀速
F=
v
P额
a=
m
F-F阻
↑
→
↓
v
↑
↓
→
→
↓
vm=
F阻
P额
加速度逐渐减小的变加速直线运动
匀速直线运动
a=
m
F-F阻
→
→
→
→
F
→
v
↑
P=F v
↑
↑
→
当P= P额时,保持P额继续加速
匀加速直线运动
机车以恒定加速度启动的v- t 图
先做匀加速直线运动,再做加速度逐渐减小的变加速直线运动,最终以速度 做匀速直线运动。
v
t
0
vm=
F阻
P额
vm
例2:
质量为m的物体在竖直向上的拉力作用下以加速度a由静止开始运动,当物体上升h高度的过程中,拉力的平均功率为多少?
F
h
a
mg
分析:
求
-
P
W=Fh
求F
牛顿第二定律
求
-
P
牛顿第二定律
求F
求末速度v
思路1
思路2
例2:
质量为m的物体在竖直向上的拉力作用下以加速度a由静止开始运动,当物体上升h高度的过程中,拉力的平均功率为多少?
F
h
a
mg
法1:
解:由牛顿第二定律:
F-mg=ma
∴ F=mg+ma= m(g+a)
W=Fh= m(g+a)h
又:h= 得:
∴ =
法2:
解:由牛顿第二定律:
F-mg=ma
∴ F=mg+ma= m(g+a)
由 得:
∴
∴ =
例3:
质量为m的物体从倾角为α的光滑斜面顶端由静止滑下,滑到斜面底端时的速度为v,求:重力的瞬时功率为多少?
V
α
mg
F1
F2
α
V
mg
法1:
解:P=mgVcos(90°-α)
=mgvsin α
法2:
解:将mg分解为沿速度方向和垂直于速度方向两个分力: F1=mg sin α
P= F1 V= mg vsin α
四、小结:
1、功率概念(与功区别联系)
(2)计算式: P=Fv
P=Fvcosα
(1)定义式:P=
(3)单位:瓦特(W)
2、平均功率和瞬时功率:
(2)瞬时功率
P=Fv
(1)平均功率:
P=
P=F
P实≤P额
3、额定功率P额和实际功率P实
4、P、F、v相互制约的关系。
2. 质量为0.2 kg的小球从高处自由下落,取g=10m/s2,则下落第三秒末重力做功的瞬时功率为________W,前三秒内重力做功的平均功率为________W。
1. 关于功率以下说法中正确的是 ( )
A.据 P=W/t可知,机器做功越多,其功率就越大
B.据 P=Fv可知,汽车牵引力一定与速度成反比
C.据 P=W/t可知,只要知道时间t内机器所做的功,就可以求得这段时间内任一时刻机器做功的功率
D.根据 P=Fv可知,发动机功率一定时,交通工具的牵引力与运动速度成反比
六、作业:
课后1、2题
创新设计
