苏科版七年级数学下册 第10章 二元一次方程组 复习课件(22张)
文档属性
| 名称 | 苏科版七年级数学下册 第10章 二元一次方程组 复习课件(22张) |  | |
| 格式 | pptx | ||
| 文件大小 | 664.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-16 15:39:22 | ||
图片预览






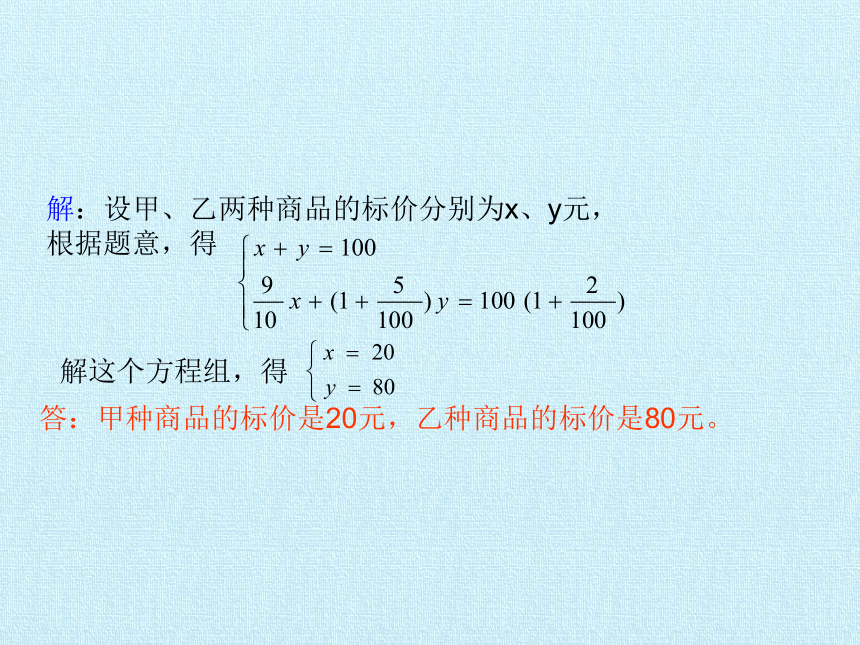
文档简介
第10章 二元一次方程组 复习课件
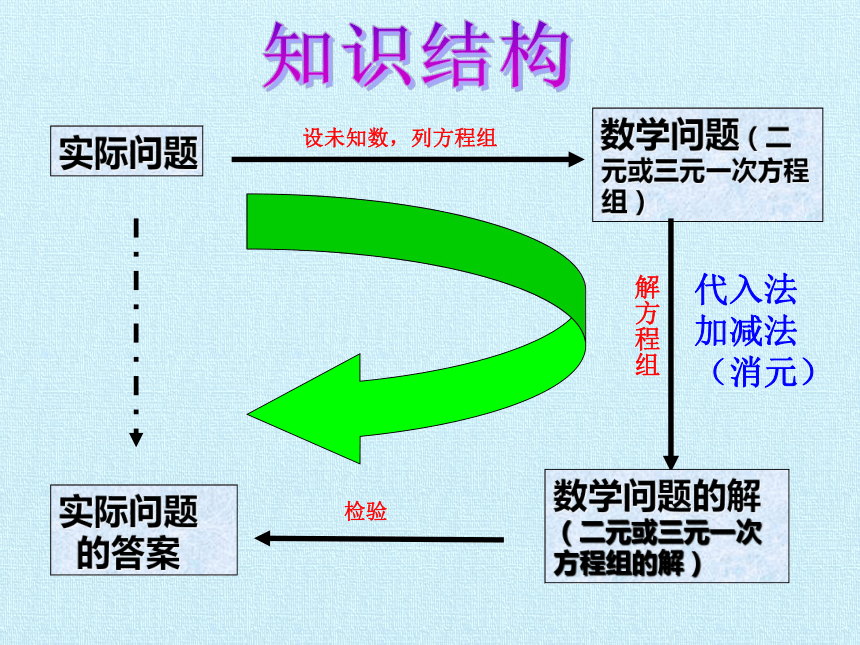
实际问题
设未知数,列方程组
数学问题(二元或三元一次方程组)
解方程组
数学问题的解(二元或三元一次
方程组的解)
检验
实际问题
的答案
代入法
加减法
(消元)
知识结构
一、二元一次方程(组)定义
有两个未知数且含未知数项的次数是一次的方程叫做二元一次方程。
1、什么是二元一次方程?
适合一个二元一次方程的一对未知数的值,叫做这个二元一次方程的一个解。
2、什么是二元一次方程组?
有两个一次方程组成,并且含有两个未知数的方程组叫做二元一次方程组。
一般地,在二元一次方程组中,使每个方程都适合的解(公共解),叫做这个二元一次方程组的解。
(2)2x+y+z=1
(5)2a+3b=5
(6)2x+10 =0
(3)x2+y=20
(4)x2+2x+1=0
(1)2x+5y=10
1、请判断下列各方程中,哪些是二元一次方程,哪些不是?并说明理由。
2、下面4组数值中,哪些是二元一次方程2x+y=10的解?
x=-2
y=6
(1)
x=3
y=4
(2)
x=4
y=3
(3)
x=6
y=-2
(4)
3、方程x+2y=7在正整数范围内的解有( )
A、1个 B、2个 C、3个 D、无数个
C
4、若x2m-1+5y3n-2m=7是二元一次方程,则m= ,n= .
1
1
5、下列是二元一次方程组的是( )
+y=3
x
1
2x+y=0
(A)
3x-1=0
2y=5
(B)
x+y=7
3y+z=4
(c)
5x -y=-2
3y+x=4
(D)
2
B
二、二元一次方程组的解法
1、解二元一次方程组的基本思想是什么?
二元一次方程组
一元一次方程
消元
转化
2、消元的方法有哪些?
代入消元法、加减消元法
例、关于x、y的二元一次方程组
的解与
的解相同,求a、b的值。
解:解方程组
得
将
代入方程组
得
解得
∴a= ,b=
审:审清题目中的等量关系
设:设未知数
列:根据等量关系,列出方程组
解:解方程组,求出未知数
验:检验所求出未知数是否符合题意
答:写出答案
三、列二元一次方程组解实际问题的一般步骤
例:已知甲、乙两种商品的标价和为100元,因市场变化,甲商品打9折,乙商品提价5﹪,调价后,甲乙两种商品的售价和比标价和提高了2﹪,求甲乙两种商品的标价各是多少?
解:设甲、乙两种商品的标价分别为x、y元,
根据题意,得
解这个方程组,得
答:甲种商品的标价是20元,乙种商品的标价是80元。
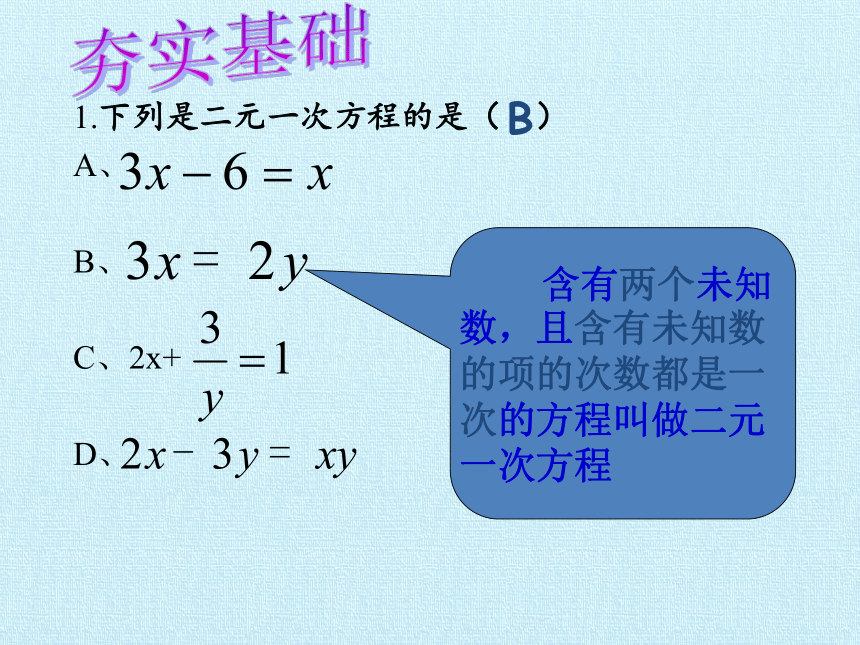
1.下列是二元一次方程的是( )
A、
B、
C、2x+
D、
B
夯实基础
含有两个未知数,且含有未知数的项的次数都是一次的方程叫做二元一次方程
2.若方程 是关于x、y的二元一次方程,则m+n= 。
1
夯实基础
由
解得
3.下列各方程组中,属于二元一次
方程组的是( )
A、 B、
C、 D、
C
由两个一次方程组成,并且含有两个未知数的方程组,叫做二元一次方程组。
夯实基础
4.在① ② ③
④ 中,是方程 的
解有 ;
是方程 的
解有 ;
①、④
①、③
方程组 的
解是
夯实基础
①
。
5.已知 是方程2x-ay=3b的一个解,
那么a-3b的值是 。
夯实基础
-2
6.在方程ax+by=10中,当x=-1时y=0,
当x=1时y=5,
解:
-a=10
由已知得:
解得:
a=-10
求a、b的值。
b=4
a+5b=10
2+a=3b
达标检测
1、已知二元一次方程组 的解是 ,则a,b的值是( )
A、 B、 C、 D、
2、若(x-3)2+|1-3y|=0,且2x-a+1=0,by-1=0,则b-a的值是( )
A、-4 B、10 C、4 D、-10
3、二元一次方程x+2y=8的非负整数解( )
A、有无数对 B、只有5对 C、只有4对 D、只有3对
4、长方形的长、宽分别为xcm,ycm,若周长为40cm,且长比宽2倍少3cm,下列方程组中,正确的是( )
A、 B、 C、 D、
B
A
B
C
5、一条船顺流航行是逆流航行的速度的3倍,这条船在静水中的航速与水的流速之比为( )
A、3:1 B、2:1 C、1:1 D、5:2
6、小明存入银行人民币若干元,年利率为2.25%,一年到期后将缴纳利息税72元(税率为利息的20%),则他存入的人民币为( )
A、1600元 B、16000元 C、360元 D、3600元
7、关于x,y的方程组 的解也是方程x+6y=-11的解,则k
=______
8、方程组 的解是_____
9、方程4x+3y=20的所有非负整数解为_______
10、快车长200m,慢车长250m,坐在慢车上的旅客看见快车从其窗口驶过的时间是6s,则坐在快车上的旅客看见慢车从其窗口驶过的时间是______s。
B
B
4
7.5
11、要把一张面值为10元的人民币换成零钱,现有足够的面值为2元、1元的人民币,共有____种换法。
12、小刚上学时步行,放学回家时乘公交车往返全程共用1.5h,如果他上学、放学时都乘公交车只需0.5h,那么他上学和放学都步行,往返全程需要用___h。
13、某种植大户计划安排10个劳动力来耕作30亩土地,这些土地可以种蔬菜也可以种水稻,种这些作物所需劳动力及预计产值如下表:
为了使所有土地种上作物,全部劳动力都有工作,应安排种蔬菜的劳动力为_人,这时预计产值为____元。
每亩所需劳动力/个
每亩预计产值/元
蔬菜
3000
水稻
700
6
2.5
5
44000
14、解方程组
15、解方程组
解:原方程组可化为:
解这个方程组得:
解:原方程组可化为:
解这个方程组得:
16、一个长方形,它的长减少1cm,宽增加3cm,所得的正方形比原来长方形的面积大21cm2,求原来长方形的面积。
解:设原长方形的长为xcm,宽为ycm。
解之得:
所以,xy=60
答:原长方形的面积为60cm2。
17、某中学新建了一栋4层的教学大楼,每层楼有8间教室,进出这栋大楼共有道门,其中两道正门大小相同,两道侧门大小也相同。安全检查中,对4道门进行了测试:当同时开启一道正门和两道侧门时,2min内可以通过560名学生;当同时开启一道正门和一道侧门时,4min内可以通过800名学生。
(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况下因学生拥挤,出门的效率将降低20%。安全检查规定,地紧急情况下,全大楼的学生应在5min内通过道门安全撤离。假设这栋教学大楼每间教室最多有45名学生,问:建造的这4道门是否符合安全规定?请说明理由。
解(1)设每分钟一道正门可通过x名学生,一道侧门可通过y名学生。
解之得:
答:平均每分钟一道正门过120名学生,一道侧门过80名学生
(2)因为5[2×120×80%+2×80×80%]=1600
而4×8×45=1440<1600
所以,符合安全规定。
18、小明寒假去外婆家,外婆给他出了一道题:“外婆家养了一些鸡和兔,共30个头和84条腿,问鸡和兔各有多少?”你能帮小明列出方程组算一算吗?
请再设计一个熟悉的问题情境,编制适当的应用问题,使其也具有类似形式的方程组。
解:设鸡有x只,兔有y只
解之得:
答:鸡的18只,兔有12只。
谢 谢
实际问题
设未知数,列方程组
数学问题(二元或三元一次方程组)
解方程组
数学问题的解(二元或三元一次
方程组的解)
检验
实际问题
的答案
代入法
加减法
(消元)
知识结构
一、二元一次方程(组)定义
有两个未知数且含未知数项的次数是一次的方程叫做二元一次方程。
1、什么是二元一次方程?
适合一个二元一次方程的一对未知数的值,叫做这个二元一次方程的一个解。
2、什么是二元一次方程组?
有两个一次方程组成,并且含有两个未知数的方程组叫做二元一次方程组。
一般地,在二元一次方程组中,使每个方程都适合的解(公共解),叫做这个二元一次方程组的解。
(2)2x+y+z=1
(5)2a+3b=5
(6)2x+10 =0
(3)x2+y=20
(4)x2+2x+1=0
(1)2x+5y=10
1、请判断下列各方程中,哪些是二元一次方程,哪些不是?并说明理由。
2、下面4组数值中,哪些是二元一次方程2x+y=10的解?
x=-2
y=6
(1)
x=3
y=4
(2)
x=4
y=3
(3)
x=6
y=-2
(4)
3、方程x+2y=7在正整数范围内的解有( )
A、1个 B、2个 C、3个 D、无数个
C
4、若x2m-1+5y3n-2m=7是二元一次方程,则m= ,n= .
1
1
5、下列是二元一次方程组的是( )
+y=3
x
1
2x+y=0
(A)
3x-1=0
2y=5
(B)
x+y=7
3y+z=4
(c)
5x -y=-2
3y+x=4
(D)
2
B
二、二元一次方程组的解法
1、解二元一次方程组的基本思想是什么?
二元一次方程组
一元一次方程
消元
转化
2、消元的方法有哪些?
代入消元法、加减消元法
例、关于x、y的二元一次方程组
的解与
的解相同,求a、b的值。
解:解方程组
得
将
代入方程组
得
解得
∴a= ,b=
审:审清题目中的等量关系
设:设未知数
列:根据等量关系,列出方程组
解:解方程组,求出未知数
验:检验所求出未知数是否符合题意
答:写出答案
三、列二元一次方程组解实际问题的一般步骤
例:已知甲、乙两种商品的标价和为100元,因市场变化,甲商品打9折,乙商品提价5﹪,调价后,甲乙两种商品的售价和比标价和提高了2﹪,求甲乙两种商品的标价各是多少?
解:设甲、乙两种商品的标价分别为x、y元,
根据题意,得
解这个方程组,得
答:甲种商品的标价是20元,乙种商品的标价是80元。
1.下列是二元一次方程的是( )
A、
B、
C、2x+
D、
B
夯实基础
含有两个未知数,且含有未知数的项的次数都是一次的方程叫做二元一次方程
2.若方程 是关于x、y的二元一次方程,则m+n= 。
1
夯实基础
由
解得
3.下列各方程组中,属于二元一次
方程组的是( )
A、 B、
C、 D、
C
由两个一次方程组成,并且含有两个未知数的方程组,叫做二元一次方程组。
夯实基础
4.在① ② ③
④ 中,是方程 的
解有 ;
是方程 的
解有 ;
①、④
①、③
方程组 的
解是
夯实基础
①
。
5.已知 是方程2x-ay=3b的一个解,
那么a-3b的值是 。
夯实基础
-2
6.在方程ax+by=10中,当x=-1时y=0,
当x=1时y=5,
解:
-a=10
由已知得:
解得:
a=-10
求a、b的值。
b=4
a+5b=10
2+a=3b
达标检测
1、已知二元一次方程组 的解是 ,则a,b的值是( )
A、 B、 C、 D、
2、若(x-3)2+|1-3y|=0,且2x-a+1=0,by-1=0,则b-a的值是( )
A、-4 B、10 C、4 D、-10
3、二元一次方程x+2y=8的非负整数解( )
A、有无数对 B、只有5对 C、只有4对 D、只有3对
4、长方形的长、宽分别为xcm,ycm,若周长为40cm,且长比宽2倍少3cm,下列方程组中,正确的是( )
A、 B、 C、 D、
B
A
B
C
5、一条船顺流航行是逆流航行的速度的3倍,这条船在静水中的航速与水的流速之比为( )
A、3:1 B、2:1 C、1:1 D、5:2
6、小明存入银行人民币若干元,年利率为2.25%,一年到期后将缴纳利息税72元(税率为利息的20%),则他存入的人民币为( )
A、1600元 B、16000元 C、360元 D、3600元
7、关于x,y的方程组 的解也是方程x+6y=-11的解,则k
=______
8、方程组 的解是_____
9、方程4x+3y=20的所有非负整数解为_______
10、快车长200m,慢车长250m,坐在慢车上的旅客看见快车从其窗口驶过的时间是6s,则坐在快车上的旅客看见慢车从其窗口驶过的时间是______s。
B
B
4
7.5
11、要把一张面值为10元的人民币换成零钱,现有足够的面值为2元、1元的人民币,共有____种换法。
12、小刚上学时步行,放学回家时乘公交车往返全程共用1.5h,如果他上学、放学时都乘公交车只需0.5h,那么他上学和放学都步行,往返全程需要用___h。
13、某种植大户计划安排10个劳动力来耕作30亩土地,这些土地可以种蔬菜也可以种水稻,种这些作物所需劳动力及预计产值如下表:
为了使所有土地种上作物,全部劳动力都有工作,应安排种蔬菜的劳动力为_人,这时预计产值为____元。
每亩所需劳动力/个
每亩预计产值/元
蔬菜
3000
水稻
700
6
2.5
5
44000
14、解方程组
15、解方程组
解:原方程组可化为:
解这个方程组得:
解:原方程组可化为:
解这个方程组得:
16、一个长方形,它的长减少1cm,宽增加3cm,所得的正方形比原来长方形的面积大21cm2,求原来长方形的面积。
解:设原长方形的长为xcm,宽为ycm。
解之得:
所以,xy=60
答:原长方形的面积为60cm2。
17、某中学新建了一栋4层的教学大楼,每层楼有8间教室,进出这栋大楼共有道门,其中两道正门大小相同,两道侧门大小也相同。安全检查中,对4道门进行了测试:当同时开启一道正门和两道侧门时,2min内可以通过560名学生;当同时开启一道正门和一道侧门时,4min内可以通过800名学生。
(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况下因学生拥挤,出门的效率将降低20%。安全检查规定,地紧急情况下,全大楼的学生应在5min内通过道门安全撤离。假设这栋教学大楼每间教室最多有45名学生,问:建造的这4道门是否符合安全规定?请说明理由。
解(1)设每分钟一道正门可通过x名学生,一道侧门可通过y名学生。
解之得:
答:平均每分钟一道正门过120名学生,一道侧门过80名学生
(2)因为5[2×120×80%+2×80×80%]=1600
而4×8×45=1440<1600
所以,符合安全规定。
18、小明寒假去外婆家,外婆给他出了一道题:“外婆家养了一些鸡和兔,共30个头和84条腿,问鸡和兔各有多少?”你能帮小明列出方程组算一算吗?
请再设计一个熟悉的问题情境,编制适当的应用问题,使其也具有类似形式的方程组。
解:设鸡有x只,兔有y只
解之得:
答:鸡的18只,兔有12只。
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
