2020六年级数学下册6整理和复习《数学思考》优质习题(含答案)新人教版
文档属性
| 名称 | 2020六年级数学下册6整理和复习《数学思考》优质习题(含答案)新人教版 | 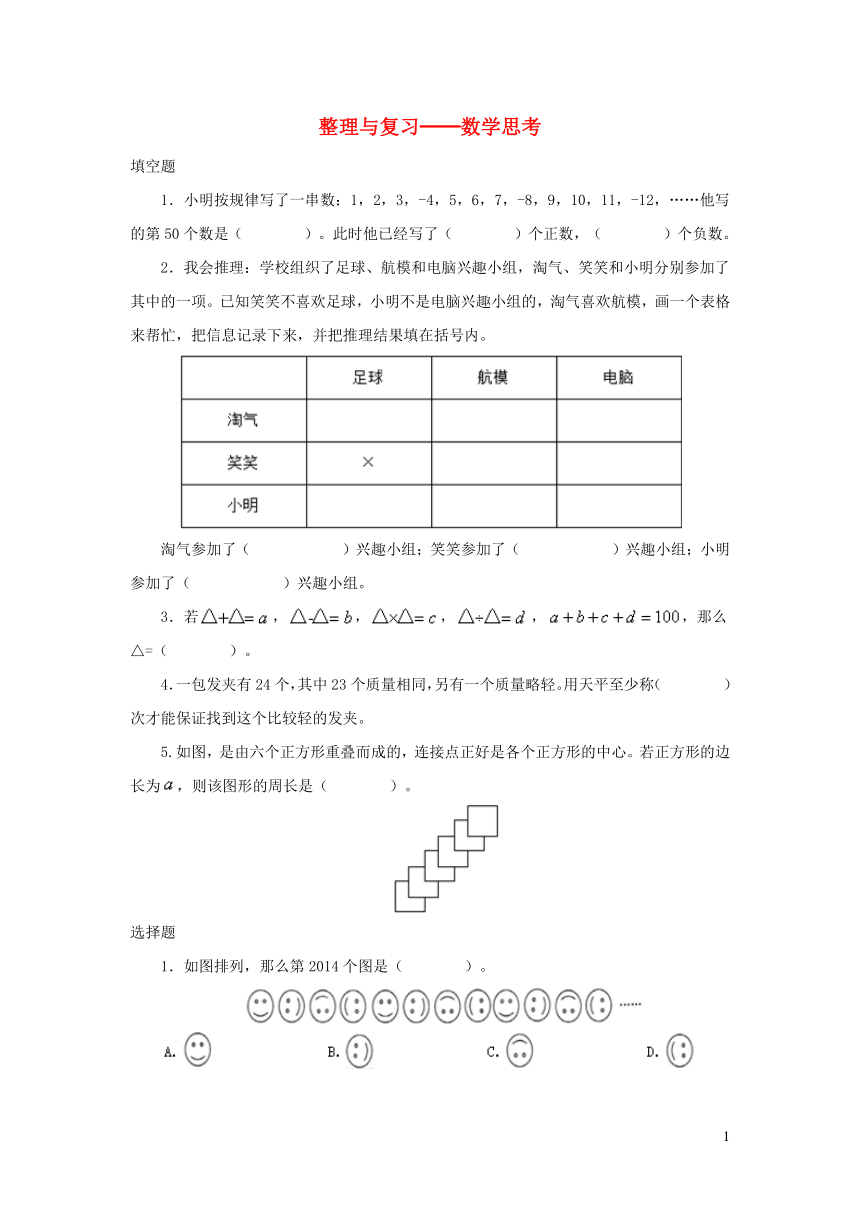 | |
| 格式 | zip | ||
| 文件大小 | 121.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-16 16:08:41 | ||
图片预览


文档简介
整理与复习──数学思考
填空题
1.小明按规律写了一串数:1,2,3,-4,5,6,7,-8,9,10,11,-12,……他写的第50个数是(????)。此时他已经写了(????)个正数,(????)个负数。
2.我会推理:学校组织了足球、航模和电脑兴趣小组,淘气、笑笑和小明分别参加了其中的一项。已知笑笑不喜欢足球,小明不是电脑兴趣小组的,淘气喜欢航模,画一个表格来帮忙,把信息记录下来,并把推理结果填在括号内。
淘气参加了(??????)兴趣小组;笑笑参加了(??????)兴趣小组;小明参加了(??????)兴趣小组。
3.若,,,,,那么△=(????)。
4.一包发夹有24个,其中23个质量相同,另有一个质量略轻。用天平至少称(????)次才能保证找到这个比较轻的发夹。
5.如图,是由六个正方形重叠而成的,连接点正好是各个正方形的中心。若正方形的边长为,则该图形的周长是(????)。
选择题
1.如图排列,那么第2014个图是(????)。
2.设“●”“▲”“■”表示三种不同的物品,用天平比较它们的重量,两次情况分别如下图所示,那么这三种物品的重量按从大到小的顺序排列为(????)。
A.■●▲?????????????
B.■▲●????????????
C.▲●■????????????
D.▲■●
3.用同样长的小棒摆成如下图所示的图形,照这样继续摆,图形⑥一共用了(????)根小棒。
A.30???????
B.25??????
C.24??????
D.20
4.一群孩子等距离围成一个圆圈玩游戏,从大毛开始按顺时针方向数,数到二毛为第8个。而且大毛和二毛正好面对面坐,这群孩子一共有(????)人。
A.16?????
?
B.14???
??
C.15???
???
D.17
5.芳芳买了6张电影票(如图),她想撕下相连的4张,共有(????)种不同的方法。
A.6????
?
B.7???
???
C.8????
?????
D.10
应用题
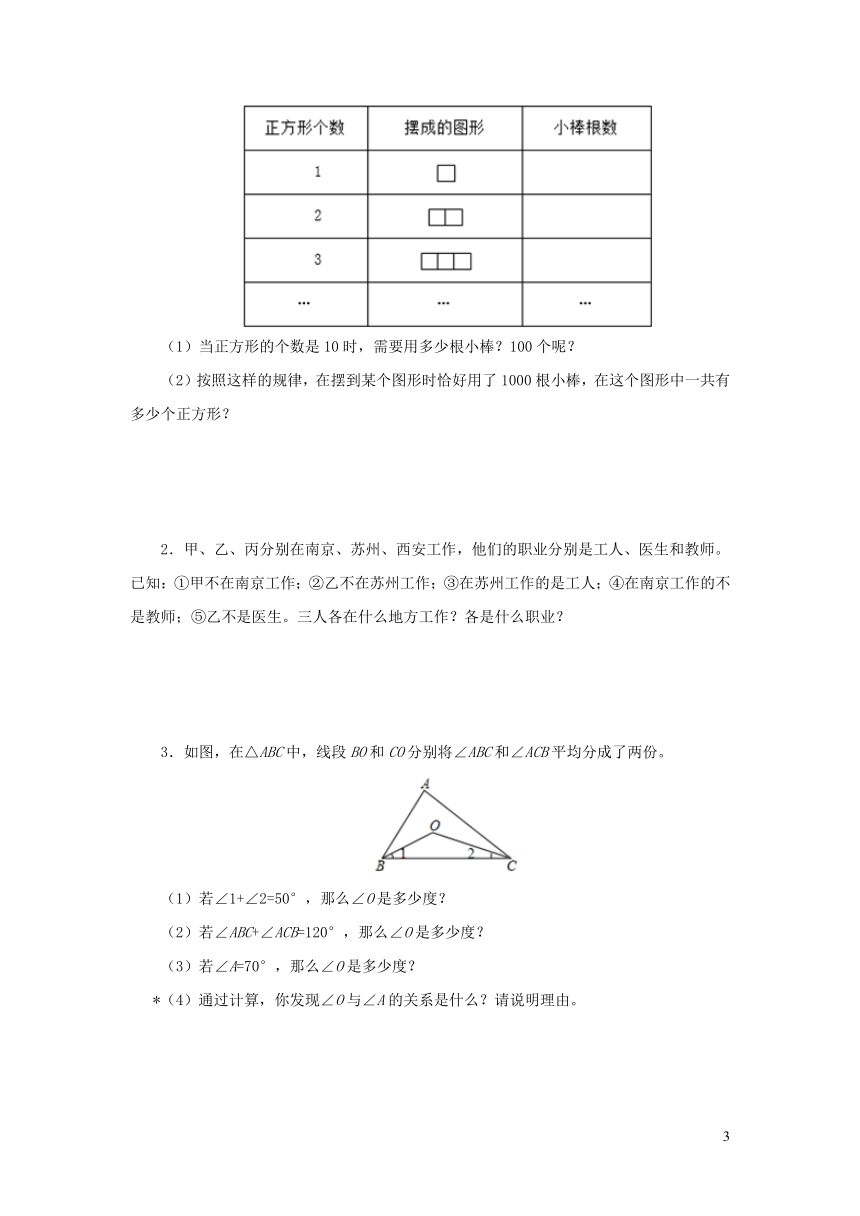
1.先填写下表,再探索出规律并解答。
(1)当正方形的个数是10时,需要用多少根小棒?100个呢?
(2)按照这样的规律,在摆到某个图形时恰好用了1000根小棒,在这个图形中一共有多少个正方形?
2.甲、乙、丙分别在南京、苏州、西安工作,他们的职业分别是工人、医生和教师。已知:①甲不在南京工作;②乙不在苏州工作;③在苏州工作的是工人;④在南京工作的不是教师;⑤乙不是医生。三人各在什么地方工作?各是什么职业?
3.如图,在△ABC中,线段BO和CO分别将∠ABC和∠ACB平均分成了两份。
(1)若∠1+∠2=50°,那么∠O是多少度?
(2)若∠ABC+∠ACB=120°,那么∠O是多少度?
(3)若∠A=70°,那么∠O是多少度?
(4)通过计算,你发现∠O与∠A的关系是什么?请说明理由。
4.如图,仪器架分三层,上层放一个大瓶和一个中瓶,中间放一个中瓶和4个小瓶,下层放6个小瓶。已知每层存放的药水量是一样多的,这个仪器架上存放的药水共36升。大瓶和中瓶中存放的药水一共有多少升?
5.把下面的图形分成大小、形状完全相同的两块,使每块中都含2005这4个数字。请你试一试。
参考答案
填空题
1.50,38,12。
2.航模,电脑,足球。表格如下:
3.9。
4.
3。
5.。
选择题
1.B。
2.B。
3.B。
4.B。
5.D。
应用题
1.(1)3×10+1=31(根)?
3×100+1=301(根)?
答:摆10个正方形需31根小棒,摆100个正方形需要301根小棒。
(2)解:设这个图形中一共有个正方形。
???
答:在用到1000根小棒的图形中,一共有333个正方形。
2.甲在苏州工作,是工人;乙在西安工作,是教师;丙在南京工作,是医生。
3.(1)∠O=180°-50°=130°
答:若∠1+∠2=50°,那么∠O是130°。
(2)∠O=180°-120°÷2=120°
答:若∠ABC+∠ACB=120°,那么∠O是120°。
(3)∠O=180°-(180°-70°)÷2=125°
答:若∠A=70°,∠O是125°。
(4)∠O=180°-(∠1+∠2)
???????
=180°-(∠ABC+∠ACB)
????
???=180°-(180°-∠A)
???????
=90°+∠A??????????????????
答:∠O等于90°加上∠A的一半。
4.12÷6=2(升)??
2×2×2+2×4=16(升)?
答:大瓶和中瓶中存放的药水一共有16升。
5.
1
填空题
1.小明按规律写了一串数:1,2,3,-4,5,6,7,-8,9,10,11,-12,……他写的第50个数是(????)。此时他已经写了(????)个正数,(????)个负数。
2.我会推理:学校组织了足球、航模和电脑兴趣小组,淘气、笑笑和小明分别参加了其中的一项。已知笑笑不喜欢足球,小明不是电脑兴趣小组的,淘气喜欢航模,画一个表格来帮忙,把信息记录下来,并把推理结果填在括号内。
淘气参加了(??????)兴趣小组;笑笑参加了(??????)兴趣小组;小明参加了(??????)兴趣小组。
3.若,,,,,那么△=(????)。
4.一包发夹有24个,其中23个质量相同,另有一个质量略轻。用天平至少称(????)次才能保证找到这个比较轻的发夹。
5.如图,是由六个正方形重叠而成的,连接点正好是各个正方形的中心。若正方形的边长为,则该图形的周长是(????)。
选择题
1.如图排列,那么第2014个图是(????)。
2.设“●”“▲”“■”表示三种不同的物品,用天平比较它们的重量,两次情况分别如下图所示,那么这三种物品的重量按从大到小的顺序排列为(????)。
A.■●▲?????????????
B.■▲●????????????
C.▲●■????????????
D.▲■●
3.用同样长的小棒摆成如下图所示的图形,照这样继续摆,图形⑥一共用了(????)根小棒。
A.30???????
B.25??????
C.24??????
D.20
4.一群孩子等距离围成一个圆圈玩游戏,从大毛开始按顺时针方向数,数到二毛为第8个。而且大毛和二毛正好面对面坐,这群孩子一共有(????)人。
A.16?????
?
B.14???
??
C.15???
???
D.17
5.芳芳买了6张电影票(如图),她想撕下相连的4张,共有(????)种不同的方法。
A.6????
?
B.7???
???
C.8????
?????
D.10
应用题
1.先填写下表,再探索出规律并解答。
(1)当正方形的个数是10时,需要用多少根小棒?100个呢?
(2)按照这样的规律,在摆到某个图形时恰好用了1000根小棒,在这个图形中一共有多少个正方形?
2.甲、乙、丙分别在南京、苏州、西安工作,他们的职业分别是工人、医生和教师。已知:①甲不在南京工作;②乙不在苏州工作;③在苏州工作的是工人;④在南京工作的不是教师;⑤乙不是医生。三人各在什么地方工作?各是什么职业?
3.如图,在△ABC中,线段BO和CO分别将∠ABC和∠ACB平均分成了两份。
(1)若∠1+∠2=50°,那么∠O是多少度?
(2)若∠ABC+∠ACB=120°,那么∠O是多少度?
(3)若∠A=70°,那么∠O是多少度?
(4)通过计算,你发现∠O与∠A的关系是什么?请说明理由。
4.如图,仪器架分三层,上层放一个大瓶和一个中瓶,中间放一个中瓶和4个小瓶,下层放6个小瓶。已知每层存放的药水量是一样多的,这个仪器架上存放的药水共36升。大瓶和中瓶中存放的药水一共有多少升?
5.把下面的图形分成大小、形状完全相同的两块,使每块中都含2005这4个数字。请你试一试。
参考答案
填空题
1.50,38,12。
2.航模,电脑,足球。表格如下:
3.9。
4.
3。
5.。
选择题
1.B。
2.B。
3.B。
4.B。
5.D。
应用题
1.(1)3×10+1=31(根)?
3×100+1=301(根)?
答:摆10个正方形需31根小棒,摆100个正方形需要301根小棒。
(2)解:设这个图形中一共有个正方形。
???
答:在用到1000根小棒的图形中,一共有333个正方形。
2.甲在苏州工作,是工人;乙在西安工作,是教师;丙在南京工作,是医生。
3.(1)∠O=180°-50°=130°
答:若∠1+∠2=50°,那么∠O是130°。
(2)∠O=180°-120°÷2=120°
答:若∠ABC+∠ACB=120°,那么∠O是120°。
(3)∠O=180°-(180°-70°)÷2=125°
答:若∠A=70°,∠O是125°。
(4)∠O=180°-(∠1+∠2)
???????
=180°-(∠ABC+∠ACB)
????
???=180°-(180°-∠A)
???????
=90°+∠A??????????????????
答:∠O等于90°加上∠A的一半。
4.12÷6=2(升)??
2×2×2+2×4=16(升)?
答:大瓶和中瓶中存放的药水一共有16升。
5.
1
