辽宁省辽阳市人教版七年级上数学3.4实际问题与一元一次方程课件 (全部类型 )(共55张PPT)
文档属性
| 名称 | 辽宁省辽阳市人教版七年级上数学3.4实际问题与一元一次方程课件 (全部类型 )(共55张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-16 23:33:24 | ||
图片预览











文档简介
(共55张PPT)
七年级数学(人教版)上册
3.4实际问题与一元一次方程
㈠知识目标:???
通过对典型实际问题的分析,学生体验从算术方法到代数方法是一种进步.
??
?㈡能力目标:???
能结合实际问题背景发现和提出数学问题。
二、过程与方法:?.???
经历“探究”的活动,激发学生的学习潜能,促使他们在自主探究与合作交流的过程中,理解和掌握基本的数学知识、技能.???
三、情感态度与价值观目标:???
引导学生关注生活及培养学生在生活中应用数学的意识.学生可能设的未知数不同,列出不同的方程,但很有利于培养学生的发散思维.?
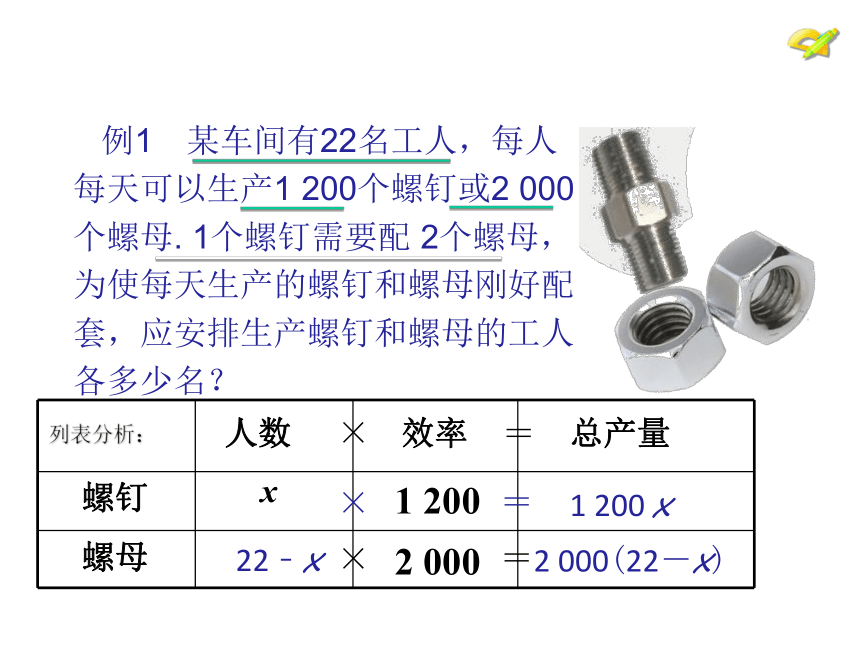
例1 某车间有22名工人,每人每天可以生产1
200个螺钉或2
000个螺母.
1个螺钉需要配
2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
人数
效率
总产量
×
列表分析:
×
=
2
000(22-x)
22﹣x
=
1
200
2
000
x
螺钉
螺母
解方程,得:
5(22-x)=6x,
110-5x=6x,
x=10.
22-x=12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
解:设应安排x名工人生产螺钉,(22-x)名工人生产螺母.
依题意得:
2
000(22-x)=2×1
200x
.
如何寻找配套问题中的等量关系?
1张桌子配4把椅子
椅子数量=
桌子数量
1把茶壶配3个茶杯
茶杯数量=
茶壶数量
2把球拍配3个乒乓球
乒乓球数量=
球拍数量
4×
3
×
桌子:椅子=1:4
1×
茶壶:茶杯=1:3
1×
球拍:球=2:3
2×
3
×
2.某纺织厂有纺织工人300名,为增产创收,该纺织厂又增设了制衣车间,准备将这300名纺织工人合理分配到纺织车间和制衣车间.现在知道工人每人每天平均能织布30米或制4件成衣,每件成衣用布1.5米,若使生产出的布匹刚好制成成衣,问应有多少人去生产成衣?
答:应有250人去生产成衣.
解:设应有x人去生产成衣.
根据题意,得
1.某水利工地派
48
人去挖土和运土,如果每人每天平均挖土5方或运土3方,那么应怎样安排人员,正好能使挖出的土及时运走?
去括号,得
5x
=
144
–3x
移项及合并,得
8x
=
144
x
=
18
运土的人数为
48
–
x
=
48
–18
=
30
答:应安排18人去挖土,30人去运土,正好能使挖出的土及时运走.
解:设安排
x
人去挖土,则有(48
–
x
)人运土,根据题意,得
5
x
=
3
(
48
–
x
)
一套仪器由一个A部件和三个B部件构成.
用1m3钢材可以做40个A部件或240个B部件.
现要用6
m3钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?
依题意得:
3×40
x=240
(6-x)
.
解方程,得:
x=4.
答:应用4
m3钢材做A部件,2
m3
钢材做B部件,配成这种仪器160套.
解:设应用
x
m3钢材做A部件,(6-x)
m3
钢材做B部件.
1、一批零件,甲每小时能加工80个,则
⑴甲3小时可加工 个零件,
x小时可加工 个零件。
⑵加工a个零件,甲需 小时完成。
2、一项工程甲独做需6天完成,则
⑴甲独做一天可完成这项工程的
⑵若乙独做比甲快2天完成,则乙独做一天可完成
这项工程的
240
80x
做一做
工程问题的基本数量关系:
工作总量=工作时间×工作效率
当不知道总工程的具体量时,一般把总工程当做“1”,如果一个人单独完成该工程需要a天,那么该人的工作效率是1/a
工程问题中的数量关系:
1)
工作效率=
2)工作总量=工作效率×工作时间
3)工作时间=
头3天甲生产
零件的个数
甲乙后5天生产零件的总个数
甲后5天生
产的个数
乙后5天生
产的个数
940个
图示
例1:甲每天生产某种零件80个,甲生产3天
后,乙也加入生产同一种零件,再经过5天,
两人共生产这种零件940个,问乙每天生产
这种零件多少个?
解:设乙每天生产零件的个数为X,由题意得:
3?80+5?80+5X=940
解得
X=60
答:乙每天生产零件60个
相等关系:全部工作量=甲独做工作量+甲、乙合作工作量
全部工作量为“1”
设甲、乙合做部分需要x小时完成,甲独做部分完成的工作量为
甲、乙合做部分完成的工作量为
例2、一件工作,甲单独做20个小时完成,乙单独做12小时完成,现在先由甲单独做4小时,剩下的部分由甲、乙合做。剩下的部分需要几小时完成?
左边
右边
解:设剩下的部分需要x小时完成,根据题意,得
注意:工作量=工作效率×工作时间
例2、一件工作,甲单独做20个小时完成,乙单独做12小时完成,现在先由甲单独做4小时,剩下的部分由甲、乙合做。剩下的部分需要几小时完成?
解这个方程,得
x=6
答:剩下的部分需要6小时完成。
解方程,得:
x=2.
答:应先安排
2人做4
h.
整理一批图书,由一个人做要40
h完成.现在计划由一部分人先做4
h,再增加2人和他们一起做8
h,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作?
解:设安排
x人先做
4
h,根据题意可得
销售问题
知识探究
1、商品原价200元,九折出售,卖价是
元.
2、商品进价是30元,售价是50元,则利润
是
元.
2、某商品原来每件零售价是a元,
现在每件降价10%,降价后每件零售价是
元.
3、某种品牌的彩电降价20%以后,每台售价为a元,则该品牌彩电每台原价应为
元.
4、某商品按定价的八折出售,售价是14.8元,则原定售价是 .
0.9a
1.25a
18.5元
180
20
思考?
对上面商品销售中的问题里有哪些量?
成本价(进价),
标价;
销售价;
利润;
盈利;
亏损:
利润率
对上面这些量有何关系?
大家想一想!
=
商品售价—商品进价
●售价、进价、利润的关系式:
商品利润
●进价、利润、利润率的关系:
利润率=
商品进价
商品利润
×100%
●标价、折扣数、商品售价关系
:
商品售价=
标价×
折扣数
10
●商品售价、进价、利润率的关系:
商品进价
商品售价=
×(1+利润率)
销
售
中
的
等
量
关
系
探究1
问题&情境
分析:售价=进价+利润
售价=(1+利润率)×进价
分析:①
设盈利25%衣服的进价是
元,则商品利润是
元;依题意列方程
由此得
x
=
②
设亏损25%衣服的进价是
元,则商品利润是
元;依题意列方程
由此得
y
=
两件衣服的进价是
x+y=
(元)
两件衣服的售价是
(元)
因为
进价
售价
所以可知卖这两件衣服总的盈亏情况是
.
x
0.25x
x
+
0.25x
=
60
48
y
-0.25y
y
+(-0.25y)=60
80
48+80=128
60×2=120
>
亏损
解:设盈利25%的那件衣服的进价是x元,
另一
件的进价为y元,依题意,得
x+0.25x=60
解得
x=48
y-0.25y=60
解得
y=80
60+60-48-80=-8(元)
答:卖这两件衣服总的亏损了8元。
(2)某文具店有两个进价不同的计算器都卖64元,其中一个盈利60%,另一个亏本20%.这次交易中的盈亏情况?
解:设盈利60%的那个计算器进价为X元,它的利润是0.6X元,则
X+0.6X=64
得
X=40
设亏本20%的那个计算器进价为Y元,它的利润是0.2Y元,则
Y–0.2Y=64
得
Y=80
所以两个计算器进价为120元,而售价128元,进价小于售价,因此两个计算器总的盈利情况为盈利8元.
请再做一做:
拓展提高
某商场把进价为800元的商品按标价的八折出售,仍获利10%,
则该商品的标价为多少元?
解:设该商品的标价为x元.
800
800
10%
x
0.8
800+800×10%=0.8x
解得 x=1100
答:设该商品的标价为1100元.
熟记下列关系式
3.4实际问题与一元一次方程
——积分问题
某次篮球联赛积分榜如下:
一、问题的引入
队名
比赛场次
胜场
负场
积分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
一、问题的引入
问题1:你能从表格中了解到哪些信息?
某次篮球联赛积分榜如下:
队名
比赛
场次
胜
场
负
场
积
分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
二、问题的探究
某次篮球联赛积分榜如下:
问题2:你能从表格中看出负一场积多少分吗?
负一场积1分
队名
比赛
场次
胜
场
负
场
积
分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
二、问题的探究
某次篮球联赛积分榜如下:
问题3:你能进一步算出胜一场积多少分吗?
设:胜一场积
x
分,
依题意,得
10x+1×4=24
解得,
x=2
∴胜一场积2分.
队名
比赛
场次
胜
场
负
场
积
分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
问题4:用式子表示总积分与胜、负场数之间的关系.
若一个队胜m场,则负(14
–
m)场,
总积分为:
2m+(14
–
m)
=
m+14
即胜m场的总积分为
m
+14
分
队名
比赛
场次
胜
场
负
场
积
分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
问题5:某队的胜场总积分能等于它的负场总积分吗?
设一个队胜x场,则负(14-x)场,
由题意得:
2x=14-x
想一想,x
表示什么量?它可以是分数吗?
由此你能得出什么结论?
队名
比赛
场次
胜
场
负
场
积
分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
结论:
用方程解决实际问题时,不仅要注意解?
方程的过程是否正确?
???????,还要注意??
方程的解是否符合问题的实际意义??。
问题6:如果去掉钢铁队的信息,你还能说出积分规则吗?
(胜一场得几分?负一场得几分?)
某次男篮联赛常规赛最终积分榜如下表:
队名
比赛场次
胜场
负场
积分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
队名
比赛场次
胜场
负场
积分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
2000赛季第12轮篮球甲A联赛部分球队积分榜:
(1)列式表示积分与胜、负场数之间的
数量关系;
(2)某队的胜场总积分能等于它的负场
总积分吗?
三、巩固应用
队名
比赛场次
胜场
负场
积分
八一双鹿
22
18
4
40
北京首钢
22
14
8
36
浙江万马
22
7
15
29
沈部雄狮
22
0
22
22
解:由积分榜最下面一行可知,负一场积1分.
设胜一场积x分,从第一行得出方程:
18x+1×4=40.
解得,x=2.
(1)如果一个队胜m场,则负(22-m)场,胜场积分为2m,负场积分为22-m,总积分为
2m+(22-m)=m+22.
(2)设一个队胜了x场,则负了(22-x)场,如果这个队的胜场总积分等于负场总结分,则
2x=22-x
解得,
三、巩固应用
∵x
(胜场)的值必须是整数
∴
不符合实际
∴没有哪个队胜场总积分等于负场总积分
练一练:
1、一次足球赛11轮(即每队均需赛11场),胜一
场记2分,平一场记1分,负一场记0分,北京国安队所负场数是所胜场数的
1/2
,
结果共得14分,求国安队共平了多少场?
2、爷爷与小明下棋(设没有平局),爷
爷胜一盘记1分,小明胜一盘记3分,下
了8盘后,两人得分相等,爷爷和小明各胜了多少盘?
解:设国安队共负了x场,则胜了2x场,平了(11-3x)场
2×2x+(11-3x)=14
解得,x=3
∴11-3x=2
答:国安队共平了2场.
解:设爷爷胜了x盘,则小明胜了(8-x)盘,
x=3(8-x)
解得,x=6
∴8-x=2
答:爷爷胜了6盘,小明胜了2盘.
3、一次数学竞赛共30题,规定答对一题得5分,
不答或错答扣2分,如果小明得了115分,则他
答对多少道题?
解:设他答对了x道题,则
5x-2(30-x)=115
解得,x=25
答:他答对了25道题.
行程问题
1.基本关系式:_________________
2.基本类型:
相遇问题;
追击问题
3.航行问题的数量关系:
(1)顺流(风)航行的路程=逆流(风)航行的路程
(2)顺水(风)速度=_________________
逆水(风)速度=_________________
路程=速度X时间
静水(无风)速+水(风)速
静水(无风)速—水(风)速
一、相遇问题的基本题型
1、同时出发(两段)
2、不同时出发
(三段
)
S甲
S乙
S甲
S乙
S总
S总
S先
S甲
S乙
S总
例1、
A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(1)若两车同时相向而行,请问B车行了多长时间后与A车相遇?
A车路程+B车路程=相距路程
线段图分析:
若设B车行了x小时后与A车相遇,显然A车相遇时也行了x小时。则A车路程为
千米;B车路程
为
千米。根据相等关系可列出方程。
相等关系:总量=各分量之和
例1、
A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(1)若两车同时相向而行,请问B车行了多长时间后与A车相遇?
A车路程+B车路程=相距路程
解:设B车行了x小时后与A车相遇,根据题意列方程得
50x+30x=240
解得
x=3
答:设B车行了3小时后与A车相遇。
例1、
A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(2)若两车同时相向而行,请问B车行了多长时间后两车相距80千米?
线段图分析:
80千米
第一种情况:
A车路程+B车路程+相距80千米=
相距路程
相等关系:总量=各分量之和
例1、
A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(2)若两车同时相向而行,请问B车行了多长时间后两车相距80千米?
线段图分析:
80千米
第二种情况:
A车路程+B车路程-相距80千米=
相距路程
1、
A、B两车分别停靠在相距115千米的甲、乙两地,A车每小时行50千米,B车每小时行30千米,A车出发1.5小时后B车再出发。
(1)若两车相向而行,请问B车行了多长时间后与A车相遇?
相等关系:A车路程+A车同走的路程+
B车同走的路程=相距路程
线段图分析:
追击问题
B路程=A先行+A后行
家
学
校
追
及
地
400米
80x米
180x米
例2、小明每天早上要在7:50之前赶到距离家1000米的学校上学,一天,小明以80米/分的速度出发,5分后,小明的爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度去追小明,并且在途中追上他。
(1)爸爸追上小明用了多少时间?
(2)追上小明时,距离学校还有多远?
追击问题
相等关系:
小明先行路程
+
小明后行路程
=爸爸的路程
B路程=A先行+A后行
家
学
校
追
及
地
400米
80x米
180x米
例2、小明每天早上要在7:50之前赶到距离家1000米的学校上学,一天,小明以80米/分的速度出发,5分后,小明的爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度去追小明,并且在途中追上他。
(1)爸爸追上小明用了多少时间?
(2)追上小明时,距离学校还有多远?
(1)解:设爸爸要
x分钟才追上小明,依题意得:
180x
=
80x
+
5×80
解得
x=4
答:爸爸追上小明用了4分钟。
3、小王、叔叔在400米长的环形跑道上练习跑步,小王每秒跑5米,叔叔每秒跑7.5米。
(1)若两人同时同地反向出发,多长时间两人首次相遇?
(2)若两人同时同地同向出发,多长时间两人首次相遇?
(1)反向
相等关系:
小王路程
+
叔叔路程
=
400
叔叔
小王
3、小王、叔叔在400米长的环形跑道上练习跑步,小王每秒跑4米,叔叔每秒跑7.5米。
(1)若两人同时同地反向出发,多长时间两人首次相遇?
(2)若两人同时同地同向出发,多长时间两人首次相遇?
(2)同向
相等关系:
小王路程
+
400
=
叔叔路程
叔叔
小王
小结:这节课我们复习了行程问题中的相遇和追及问题,归纳如下:
相等关系:A车路程+B车路程=相距路程
相等关系:
B车路程=A车先路程+A车后行路程
或B车路程=A车路程+相距路程
七年级数学(人教版)上册
3.4实际问题与一元一次方程
㈠知识目标:???
通过对典型实际问题的分析,学生体验从算术方法到代数方法是一种进步.
??
?㈡能力目标:???
能结合实际问题背景发现和提出数学问题。
二、过程与方法:?.???
经历“探究”的活动,激发学生的学习潜能,促使他们在自主探究与合作交流的过程中,理解和掌握基本的数学知识、技能.???
三、情感态度与价值观目标:???
引导学生关注生活及培养学生在生活中应用数学的意识.学生可能设的未知数不同,列出不同的方程,但很有利于培养学生的发散思维.?
例1 某车间有22名工人,每人每天可以生产1
200个螺钉或2
000个螺母.
1个螺钉需要配
2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
人数
效率
总产量
×
列表分析:
×
=
2
000(22-x)
22﹣x
=
1
200
2
000
x
螺钉
螺母
解方程,得:
5(22-x)=6x,
110-5x=6x,
x=10.
22-x=12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
解:设应安排x名工人生产螺钉,(22-x)名工人生产螺母.
依题意得:
2
000(22-x)=2×1
200x
.
如何寻找配套问题中的等量关系?
1张桌子配4把椅子
椅子数量=
桌子数量
1把茶壶配3个茶杯
茶杯数量=
茶壶数量
2把球拍配3个乒乓球
乒乓球数量=
球拍数量
4×
3
×
桌子:椅子=1:4
1×
茶壶:茶杯=1:3
1×
球拍:球=2:3
2×
3
×
2.某纺织厂有纺织工人300名,为增产创收,该纺织厂又增设了制衣车间,准备将这300名纺织工人合理分配到纺织车间和制衣车间.现在知道工人每人每天平均能织布30米或制4件成衣,每件成衣用布1.5米,若使生产出的布匹刚好制成成衣,问应有多少人去生产成衣?
答:应有250人去生产成衣.
解:设应有x人去生产成衣.
根据题意,得
1.某水利工地派
48
人去挖土和运土,如果每人每天平均挖土5方或运土3方,那么应怎样安排人员,正好能使挖出的土及时运走?
去括号,得
5x
=
144
–3x
移项及合并,得
8x
=
144
x
=
18
运土的人数为
48
–
x
=
48
–18
=
30
答:应安排18人去挖土,30人去运土,正好能使挖出的土及时运走.
解:设安排
x
人去挖土,则有(48
–
x
)人运土,根据题意,得
5
x
=
3
(
48
–
x
)
一套仪器由一个A部件和三个B部件构成.
用1m3钢材可以做40个A部件或240个B部件.
现要用6
m3钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?
依题意得:
3×40
x=240
(6-x)
.
解方程,得:
x=4.
答:应用4
m3钢材做A部件,2
m3
钢材做B部件,配成这种仪器160套.
解:设应用
x
m3钢材做A部件,(6-x)
m3
钢材做B部件.
1、一批零件,甲每小时能加工80个,则
⑴甲3小时可加工 个零件,
x小时可加工 个零件。
⑵加工a个零件,甲需 小时完成。
2、一项工程甲独做需6天完成,则
⑴甲独做一天可完成这项工程的
⑵若乙独做比甲快2天完成,则乙独做一天可完成
这项工程的
240
80x
做一做
工程问题的基本数量关系:
工作总量=工作时间×工作效率
当不知道总工程的具体量时,一般把总工程当做“1”,如果一个人单独完成该工程需要a天,那么该人的工作效率是1/a
工程问题中的数量关系:
1)
工作效率=
2)工作总量=工作效率×工作时间
3)工作时间=
头3天甲生产
零件的个数
甲乙后5天生产零件的总个数
甲后5天生
产的个数
乙后5天生
产的个数
940个
图示
例1:甲每天生产某种零件80个,甲生产3天
后,乙也加入生产同一种零件,再经过5天,
两人共生产这种零件940个,问乙每天生产
这种零件多少个?
解:设乙每天生产零件的个数为X,由题意得:
3?80+5?80+5X=940
解得
X=60
答:乙每天生产零件60个
相等关系:全部工作量=甲独做工作量+甲、乙合作工作量
全部工作量为“1”
设甲、乙合做部分需要x小时完成,甲独做部分完成的工作量为
甲、乙合做部分完成的工作量为
例2、一件工作,甲单独做20个小时完成,乙单独做12小时完成,现在先由甲单独做4小时,剩下的部分由甲、乙合做。剩下的部分需要几小时完成?
左边
右边
解:设剩下的部分需要x小时完成,根据题意,得
注意:工作量=工作效率×工作时间
例2、一件工作,甲单独做20个小时完成,乙单独做12小时完成,现在先由甲单独做4小时,剩下的部分由甲、乙合做。剩下的部分需要几小时完成?
解这个方程,得
x=6
答:剩下的部分需要6小时完成。
解方程,得:
x=2.
答:应先安排
2人做4
h.
整理一批图书,由一个人做要40
h完成.现在计划由一部分人先做4
h,再增加2人和他们一起做8
h,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作?
解:设安排
x人先做
4
h,根据题意可得
销售问题
知识探究
1、商品原价200元,九折出售,卖价是
元.
2、商品进价是30元,售价是50元,则利润
是
元.
2、某商品原来每件零售价是a元,
现在每件降价10%,降价后每件零售价是
元.
3、某种品牌的彩电降价20%以后,每台售价为a元,则该品牌彩电每台原价应为
元.
4、某商品按定价的八折出售,售价是14.8元,则原定售价是 .
0.9a
1.25a
18.5元
180
20
思考?
对上面商品销售中的问题里有哪些量?
成本价(进价),
标价;
销售价;
利润;
盈利;
亏损:
利润率
对上面这些量有何关系?
大家想一想!
=
商品售价—商品进价
●售价、进价、利润的关系式:
商品利润
●进价、利润、利润率的关系:
利润率=
商品进价
商品利润
×100%
●标价、折扣数、商品售价关系
:
商品售价=
标价×
折扣数
10
●商品售价、进价、利润率的关系:
商品进价
商品售价=
×(1+利润率)
销
售
中
的
等
量
关
系
探究1
问题&情境
分析:售价=进价+利润
售价=(1+利润率)×进价
分析:①
设盈利25%衣服的进价是
元,则商品利润是
元;依题意列方程
由此得
x
=
②
设亏损25%衣服的进价是
元,则商品利润是
元;依题意列方程
由此得
y
=
两件衣服的进价是
x+y=
(元)
两件衣服的售价是
(元)
因为
进价
售价
所以可知卖这两件衣服总的盈亏情况是
.
x
0.25x
x
+
0.25x
=
60
48
y
-0.25y
y
+(-0.25y)=60
80
48+80=128
60×2=120
>
亏损
解:设盈利25%的那件衣服的进价是x元,
另一
件的进价为y元,依题意,得
x+0.25x=60
解得
x=48
y-0.25y=60
解得
y=80
60+60-48-80=-8(元)
答:卖这两件衣服总的亏损了8元。
(2)某文具店有两个进价不同的计算器都卖64元,其中一个盈利60%,另一个亏本20%.这次交易中的盈亏情况?
解:设盈利60%的那个计算器进价为X元,它的利润是0.6X元,则
X+0.6X=64
得
X=40
设亏本20%的那个计算器进价为Y元,它的利润是0.2Y元,则
Y–0.2Y=64
得
Y=80
所以两个计算器进价为120元,而售价128元,进价小于售价,因此两个计算器总的盈利情况为盈利8元.
请再做一做:
拓展提高
某商场把进价为800元的商品按标价的八折出售,仍获利10%,
则该商品的标价为多少元?
解:设该商品的标价为x元.
800
800
10%
x
0.8
800+800×10%=0.8x
解得 x=1100
答:设该商品的标价为1100元.
熟记下列关系式
3.4实际问题与一元一次方程
——积分问题
某次篮球联赛积分榜如下:
一、问题的引入
队名
比赛场次
胜场
负场
积分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
一、问题的引入
问题1:你能从表格中了解到哪些信息?
某次篮球联赛积分榜如下:
队名
比赛
场次
胜
场
负
场
积
分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
二、问题的探究
某次篮球联赛积分榜如下:
问题2:你能从表格中看出负一场积多少分吗?
负一场积1分
队名
比赛
场次
胜
场
负
场
积
分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
二、问题的探究
某次篮球联赛积分榜如下:
问题3:你能进一步算出胜一场积多少分吗?
设:胜一场积
x
分,
依题意,得
10x+1×4=24
解得,
x=2
∴胜一场积2分.
队名
比赛
场次
胜
场
负
场
积
分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
问题4:用式子表示总积分与胜、负场数之间的关系.
若一个队胜m场,则负(14
–
m)场,
总积分为:
2m+(14
–
m)
=
m+14
即胜m场的总积分为
m
+14
分
队名
比赛
场次
胜
场
负
场
积
分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
问题5:某队的胜场总积分能等于它的负场总积分吗?
设一个队胜x场,则负(14-x)场,
由题意得:
2x=14-x
想一想,x
表示什么量?它可以是分数吗?
由此你能得出什么结论?
队名
比赛
场次
胜
场
负
场
积
分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
结论:
用方程解决实际问题时,不仅要注意解?
方程的过程是否正确?
???????,还要注意??
方程的解是否符合问题的实际意义??。
问题6:如果去掉钢铁队的信息,你还能说出积分规则吗?
(胜一场得几分?负一场得几分?)
某次男篮联赛常规赛最终积分榜如下表:
队名
比赛场次
胜场
负场
积分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
雄鹰
14
7
7
21
远大
14
7
7
21
卫星
14
4
10
18
钢铁
14
0
14
14
队名
比赛场次
胜场
负场
积分
前进
14
10
4
24
东方
14
10
4
24
光明
14
9
5
23
蓝天
14
9
5
23
2000赛季第12轮篮球甲A联赛部分球队积分榜:
(1)列式表示积分与胜、负场数之间的
数量关系;
(2)某队的胜场总积分能等于它的负场
总积分吗?
三、巩固应用
队名
比赛场次
胜场
负场
积分
八一双鹿
22
18
4
40
北京首钢
22
14
8
36
浙江万马
22
7
15
29
沈部雄狮
22
0
22
22
解:由积分榜最下面一行可知,负一场积1分.
设胜一场积x分,从第一行得出方程:
18x+1×4=40.
解得,x=2.
(1)如果一个队胜m场,则负(22-m)场,胜场积分为2m,负场积分为22-m,总积分为
2m+(22-m)=m+22.
(2)设一个队胜了x场,则负了(22-x)场,如果这个队的胜场总积分等于负场总结分,则
2x=22-x
解得,
三、巩固应用
∵x
(胜场)的值必须是整数
∴
不符合实际
∴没有哪个队胜场总积分等于负场总积分
练一练:
1、一次足球赛11轮(即每队均需赛11场),胜一
场记2分,平一场记1分,负一场记0分,北京国安队所负场数是所胜场数的
1/2
,
结果共得14分,求国安队共平了多少场?
2、爷爷与小明下棋(设没有平局),爷
爷胜一盘记1分,小明胜一盘记3分,下
了8盘后,两人得分相等,爷爷和小明各胜了多少盘?
解:设国安队共负了x场,则胜了2x场,平了(11-3x)场
2×2x+(11-3x)=14
解得,x=3
∴11-3x=2
答:国安队共平了2场.
解:设爷爷胜了x盘,则小明胜了(8-x)盘,
x=3(8-x)
解得,x=6
∴8-x=2
答:爷爷胜了6盘,小明胜了2盘.
3、一次数学竞赛共30题,规定答对一题得5分,
不答或错答扣2分,如果小明得了115分,则他
答对多少道题?
解:设他答对了x道题,则
5x-2(30-x)=115
解得,x=25
答:他答对了25道题.
行程问题
1.基本关系式:_________________
2.基本类型:
相遇问题;
追击问题
3.航行问题的数量关系:
(1)顺流(风)航行的路程=逆流(风)航行的路程
(2)顺水(风)速度=_________________
逆水(风)速度=_________________
路程=速度X时间
静水(无风)速+水(风)速
静水(无风)速—水(风)速
一、相遇问题的基本题型
1、同时出发(两段)
2、不同时出发
(三段
)
S甲
S乙
S甲
S乙
S总
S总
S先
S甲
S乙
S总
例1、
A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(1)若两车同时相向而行,请问B车行了多长时间后与A车相遇?
A车路程+B车路程=相距路程
线段图分析:
若设B车行了x小时后与A车相遇,显然A车相遇时也行了x小时。则A车路程为
千米;B车路程
为
千米。根据相等关系可列出方程。
相等关系:总量=各分量之和
例1、
A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(1)若两车同时相向而行,请问B车行了多长时间后与A车相遇?
A车路程+B车路程=相距路程
解:设B车行了x小时后与A车相遇,根据题意列方程得
50x+30x=240
解得
x=3
答:设B车行了3小时后与A车相遇。
例1、
A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(2)若两车同时相向而行,请问B车行了多长时间后两车相距80千米?
线段图分析:
80千米
第一种情况:
A车路程+B车路程+相距80千米=
相距路程
相等关系:总量=各分量之和
例1、
A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(2)若两车同时相向而行,请问B车行了多长时间后两车相距80千米?
线段图分析:
80千米
第二种情况:
A车路程+B车路程-相距80千米=
相距路程
1、
A、B两车分别停靠在相距115千米的甲、乙两地,A车每小时行50千米,B车每小时行30千米,A车出发1.5小时后B车再出发。
(1)若两车相向而行,请问B车行了多长时间后与A车相遇?
相等关系:A车路程+A车同走的路程+
B车同走的路程=相距路程
线段图分析:
追击问题
B路程=A先行+A后行
家
学
校
追
及
地
400米
80x米
180x米
例2、小明每天早上要在7:50之前赶到距离家1000米的学校上学,一天,小明以80米/分的速度出发,5分后,小明的爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度去追小明,并且在途中追上他。
(1)爸爸追上小明用了多少时间?
(2)追上小明时,距离学校还有多远?
追击问题
相等关系:
小明先行路程
+
小明后行路程
=爸爸的路程
B路程=A先行+A后行
家
学
校
追
及
地
400米
80x米
180x米
例2、小明每天早上要在7:50之前赶到距离家1000米的学校上学,一天,小明以80米/分的速度出发,5分后,小明的爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度去追小明,并且在途中追上他。
(1)爸爸追上小明用了多少时间?
(2)追上小明时,距离学校还有多远?
(1)解:设爸爸要
x分钟才追上小明,依题意得:
180x
=
80x
+
5×80
解得
x=4
答:爸爸追上小明用了4分钟。
3、小王、叔叔在400米长的环形跑道上练习跑步,小王每秒跑5米,叔叔每秒跑7.5米。
(1)若两人同时同地反向出发,多长时间两人首次相遇?
(2)若两人同时同地同向出发,多长时间两人首次相遇?
(1)反向
相等关系:
小王路程
+
叔叔路程
=
400
叔叔
小王
3、小王、叔叔在400米长的环形跑道上练习跑步,小王每秒跑4米,叔叔每秒跑7.5米。
(1)若两人同时同地反向出发,多长时间两人首次相遇?
(2)若两人同时同地同向出发,多长时间两人首次相遇?
(2)同向
相等关系:
小王路程
+
400
=
叔叔路程
叔叔
小王
小结:这节课我们复习了行程问题中的相遇和追及问题,归纳如下:
相等关系:A车路程+B车路程=相距路程
相等关系:
B车路程=A车先路程+A车后行路程
或B车路程=A车路程+相距路程
