苏教版九年级数学下册 第7章 锐角三角函数课件(27张ppt)
文档属性
| 名称 | 苏教版九年级数学下册 第7章 锐角三角函数课件(27张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 573.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-16 00:00:00 | ||
图片预览






文档简介
第7章 锐角三角函数 复习课件
学习目标
知识回顾
典型例题和及时反馈
学习目标
1.巩固三角函数的概念,巩固用直角三角形边之比来表示某个锐角的三角函数。
2.熟记30°,45°, 60°角的三角函数值。会计算含有特殊角的三角函数的值,会由一个特殊锐角的三角函数值,求出它的对应的角度。
3.掌握直角三角形的边角关系,会运用勾股定理,直角三角形的两锐角互余及锐角三角函数解直角三角形。
4.会用解直角三角形的有关知识解决简单的实际问题。
锐角三角函数
1.锐角三角函数的定义
⑴正弦
⑵余弦
⑶正切
2.30°、45°、60°特殊角的三角函数值
3.解直角三角形
⑴定义
⑵解直角三角形的依据
①三边间关系
②锐角间关系
③边角间关系
⑶解直角三角形在实际问题中
的应用
知识回顾
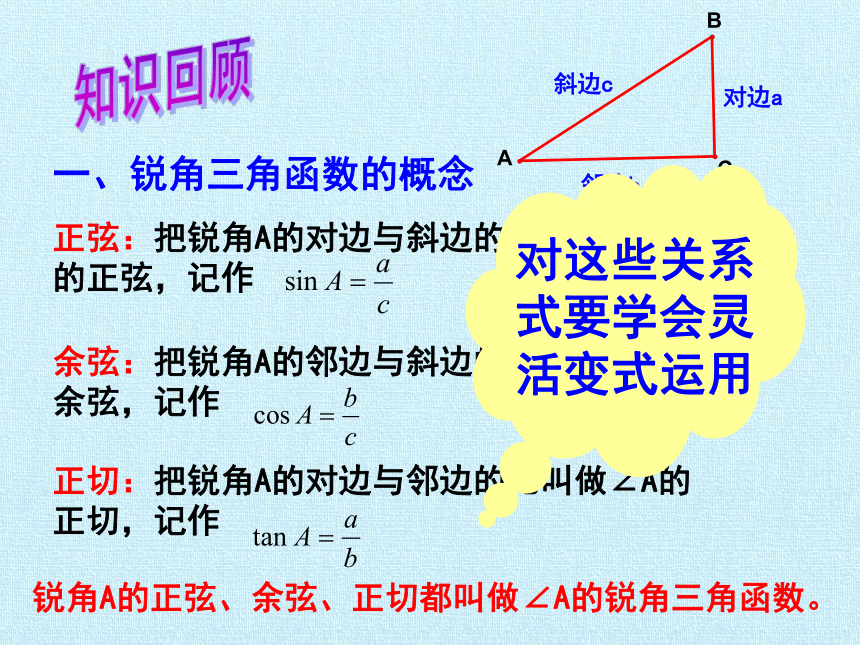
一、锐角三角函数的概念
正弦:把锐角A的对边与斜边的比叫做∠A的正弦,记作
余弦:把锐角A的邻边与斜边的比叫做∠A的余弦,记作
正切:把锐角A的对边与邻边的比叫做∠A的正切,记作
对边a
邻边b
斜边c
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数。
对这些关系式要学会灵活变式运用
同一锐角的正弦值和余弦值之间的关系是:正弦值等于它的余角的余弦值,余弦值等于它的余角的正弦值。
sinA=cos(90°一A)=cosB cosA=sin(90°一A)=sinB
知识回顾
思考:同一个锐角的正弦值和余弦值之间有何关系?
知识回顾
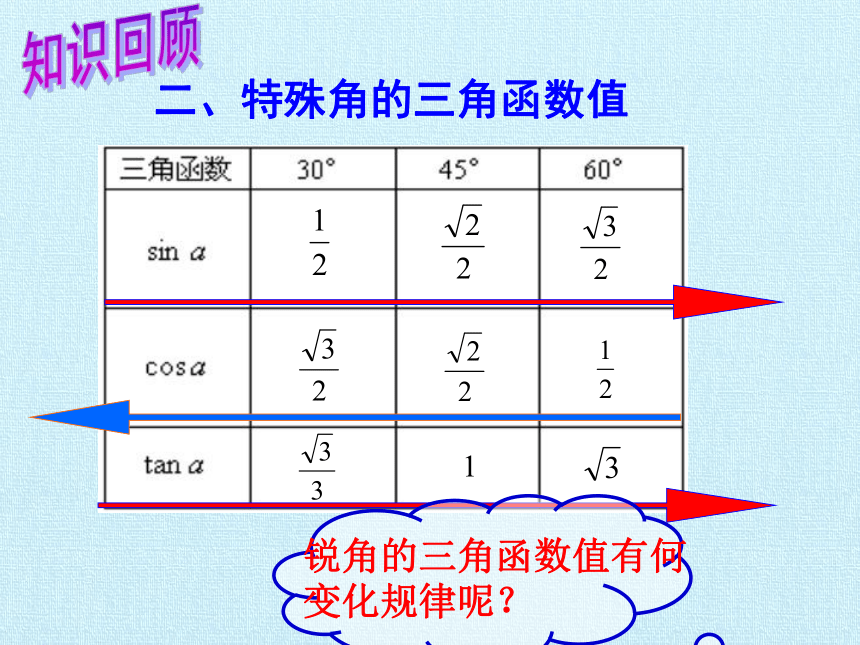
二、特殊角的三角函数值
锐角的三角函数值有何变化规律呢?
知识回顾
三、解直角三角形
由直角三角形中,除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形。
1.什么叫解直角三角形?
2.直角三角形中的边角关系:
∠A十∠B=90°
归纳:只要知道其中的2个元素(至少有一个是边),就可以求出其余3个未知元素。
(1)三边关系:
(勾股定理)
(2)两锐角的关系:
(3)边角的关系:
知识回顾
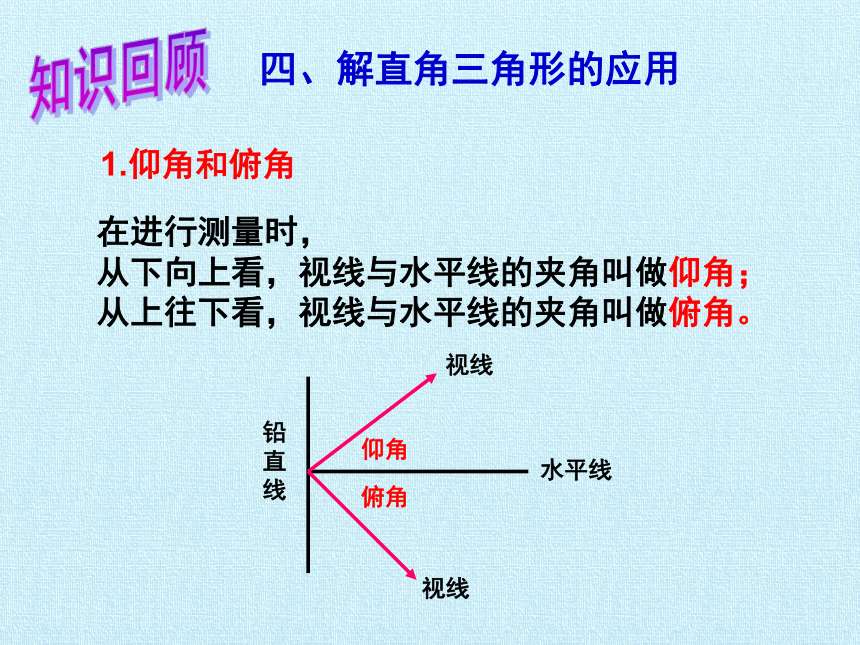
四、解直角三角形的应用
1.仰角和俯角
在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角。
铅直线
水平线
视线
视线
仰角
俯角
坡度(坡比):坡面的铅
直高度h和水平距离l的
比叫做坡度,用字母i表
示,则
2.坡度、坡角
坡角:坡面与水平面的夹角叫做坡角,用字母α表示。
h
l
知识回顾
坡度通常写成 的形式。
典型例题
解:原式=2× +1×
=1+
例1.计算2sin30 °+tan45°×cos60°
=
步骤:
一“代”二“算”
例2.若 ,则锐角α=
30°
点拨:本题是由特殊角的三角函数值求角度,首先
将原式变形为tanα= ,从而求得α的度数。
典型例题
例3.在Rt △ ABC中,∠C=90°,∠ A=30°,a=5,求b、c的大小。
解:
∵ sinA=a/c,
∴ c=a/sinA=5/sin30=5/(1/2)=10。
A
B
C
5
30°
∠B=90°- ∠ A=90°-30°=60°,
∵tanB=b/a,
∴b=a·tanB=5·tan60°=
解直角三角形分为两类:一是已知一边一角解直角三角形;二是已知两边解直角三角形。
典型例题
例4.如图,在△ABC中,AD是BC边上的高,
若tanB=cos∠DAC。
(1)AC与BD相等吗?说明理由;
D
C
B
A
故 BD=AC
解:(1)
在Rt △ABD和△ACD中,tanB= , =
因为tanB=cos∠DAC,所以 =
cos∠DAC
(2)若sinC= ,BC=12,求AD的长。
典型例题
例4.如图,在△ABC中,AD是BC边上的高,
若tanB=cos∠DAC。
(1)AC与BD相等吗?说明理由;
D
C
B
A
(2)若sinC= ,BC=12,求AD的长。
设AC=13k,AD=12k,所以CD=5k,又AC=BD=13k,
(2)在Rt △ACD中,因为sinC=
所以BC=18k=12,故k=
所以AD=12× =8
及时反馈
1.若 ,则锐角α=
2.若 ,则锐角α=
3.计算:
45°
80°
4.如图,在Rt△ABC中,∠C=90,b= ,c=4。
则a= ,∠B= ,∠A= 。
A
B
C
2
60°
30°
及时反馈
D
5.如果
那么△ABC是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
典型例题
例5.海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上。如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由。
D
分析:作PD⊥BC,设PD=x,则BD=x,AD=x+12,根据AD= PD,得x+12= x,求出x的值,再比较PD与18的大小关系。
解:有触礁危险。
理由:过点P作PD⊥AC于D。设PD为x,在Rt△PBD中,∠PBD=90°-45°=45°。∴BD=PD=x,AD=12+x。
在Rt△PAD中,∵∠PAD=90°-60°=30°,
∴渔船不改变航线继续向东航行,有触礁危险。
典型例题
D
典型例题
例6.我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,如图所示,BC∥AD,斜坡AB=40米,坡角∠BAD=60°,为防夏季因瀑雨引发山体滑坡,保障安全,学校决定对山坡进行改造。经地质人员勘测,当坡角不超过45°时,可确保山体不滑坡,改造时保持坡脚A不动,从坡顶B沿BC削进到E处,问BE至少是多少米(结果保留根号)?
G
F
分析:就是当∠EAD=45°时,求BE的长,作BF⊥AD,EG⊥AD,则BE=GF=AG-AF。
典型例题
过点B作BF⊥AD,在Rt△ABF中,AB=40,∠BAD=60°,
过点E作EG⊥AD,在Rt△ABF中,GE=BF
当∠EAD=45°时,
点评:题目中没有直角三角形时,我们可以作辅助线构造直角三角形,作辅助线时要考虑如何充分和便利的使用已知条件。
G
F
解:
6.直角三角形纸片的两直角边分别BC为6,AC为8,现将△ABC,按如图折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是 。
A
B
C
6
8
E
D
方法点拨:设CE=x,则AE=BE=8-x,利用勾股定理求出x,再求tan∠CBE的值。
及时反馈
及时反馈
7.如图,某数学兴趣小组在活动课上测量学校旗杆高度。已知小明的眼睛与地面的距离是1.7m,看旗杆顶部的仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,看旗杆顶部的仰角为30°。两人相距28米且位于旗杆两侧(点B,N,D在同一条直线上)。请求出旗杆MN的高度。(结果保留整数)
MN=12米
8.如图,甲船在港口P的北偏西60°方向,距港口80海里的A处,沿AP方向以12海里/时的速度驶向港口P。乙船从港口P出发,沿北偏东45°方向匀速驶离港口P,现两船同时出发,2小时后乙船在甲船的正东方向,求乙船的航行速度。
及时反馈
谢 谢
学习目标
知识回顾
典型例题和及时反馈
学习目标
1.巩固三角函数的概念,巩固用直角三角形边之比来表示某个锐角的三角函数。
2.熟记30°,45°, 60°角的三角函数值。会计算含有特殊角的三角函数的值,会由一个特殊锐角的三角函数值,求出它的对应的角度。
3.掌握直角三角形的边角关系,会运用勾股定理,直角三角形的两锐角互余及锐角三角函数解直角三角形。
4.会用解直角三角形的有关知识解决简单的实际问题。
锐角三角函数
1.锐角三角函数的定义
⑴正弦
⑵余弦
⑶正切
2.30°、45°、60°特殊角的三角函数值
3.解直角三角形
⑴定义
⑵解直角三角形的依据
①三边间关系
②锐角间关系
③边角间关系
⑶解直角三角形在实际问题中
的应用
知识回顾
一、锐角三角函数的概念
正弦:把锐角A的对边与斜边的比叫做∠A的正弦,记作
余弦:把锐角A的邻边与斜边的比叫做∠A的余弦,记作
正切:把锐角A的对边与邻边的比叫做∠A的正切,记作
对边a
邻边b
斜边c
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数。
对这些关系式要学会灵活变式运用
同一锐角的正弦值和余弦值之间的关系是:正弦值等于它的余角的余弦值,余弦值等于它的余角的正弦值。
sinA=cos(90°一A)=cosB cosA=sin(90°一A)=sinB
知识回顾
思考:同一个锐角的正弦值和余弦值之间有何关系?
知识回顾
二、特殊角的三角函数值
锐角的三角函数值有何变化规律呢?
知识回顾
三、解直角三角形
由直角三角形中,除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形。
1.什么叫解直角三角形?
2.直角三角形中的边角关系:
∠A十∠B=90°
归纳:只要知道其中的2个元素(至少有一个是边),就可以求出其余3个未知元素。
(1)三边关系:
(勾股定理)
(2)两锐角的关系:
(3)边角的关系:
知识回顾
四、解直角三角形的应用
1.仰角和俯角
在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角。
铅直线
水平线
视线
视线
仰角
俯角
坡度(坡比):坡面的铅
直高度h和水平距离l的
比叫做坡度,用字母i表
示,则
2.坡度、坡角
坡角:坡面与水平面的夹角叫做坡角,用字母α表示。
h
l
知识回顾
坡度通常写成 的形式。
典型例题
解:原式=2× +1×
=1+
例1.计算2sin30 °+tan45°×cos60°
=
步骤:
一“代”二“算”
例2.若 ,则锐角α=
30°
点拨:本题是由特殊角的三角函数值求角度,首先
将原式变形为tanα= ,从而求得α的度数。
典型例题
例3.在Rt △ ABC中,∠C=90°,∠ A=30°,a=5,求b、c的大小。
解:
∵ sinA=a/c,
∴ c=a/sinA=5/sin30=5/(1/2)=10。
A
B
C
5
30°
∠B=90°- ∠ A=90°-30°=60°,
∵tanB=b/a,
∴b=a·tanB=5·tan60°=
解直角三角形分为两类:一是已知一边一角解直角三角形;二是已知两边解直角三角形。
典型例题
例4.如图,在△ABC中,AD是BC边上的高,
若tanB=cos∠DAC。
(1)AC与BD相等吗?说明理由;
D
C
B
A
故 BD=AC
解:(1)
在Rt △ABD和△ACD中,tanB= , =
因为tanB=cos∠DAC,所以 =
cos∠DAC
(2)若sinC= ,BC=12,求AD的长。
典型例题
例4.如图,在△ABC中,AD是BC边上的高,
若tanB=cos∠DAC。
(1)AC与BD相等吗?说明理由;
D
C
B
A
(2)若sinC= ,BC=12,求AD的长。
设AC=13k,AD=12k,所以CD=5k,又AC=BD=13k,
(2)在Rt △ACD中,因为sinC=
所以BC=18k=12,故k=
所以AD=12× =8
及时反馈
1.若 ,则锐角α=
2.若 ,则锐角α=
3.计算:
45°
80°
4.如图,在Rt△ABC中,∠C=90,b= ,c=4。
则a= ,∠B= ,∠A= 。
A
B
C
2
60°
30°
及时反馈
D
5.如果
那么△ABC是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
典型例题
例5.海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上。如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由。
D
分析:作PD⊥BC,设PD=x,则BD=x,AD=x+12,根据AD= PD,得x+12= x,求出x的值,再比较PD与18的大小关系。
解:有触礁危险。
理由:过点P作PD⊥AC于D。设PD为x,在Rt△PBD中,∠PBD=90°-45°=45°。∴BD=PD=x,AD=12+x。
在Rt△PAD中,∵∠PAD=90°-60°=30°,
∴渔船不改变航线继续向东航行,有触礁危险。
典型例题
D
典型例题
例6.我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,如图所示,BC∥AD,斜坡AB=40米,坡角∠BAD=60°,为防夏季因瀑雨引发山体滑坡,保障安全,学校决定对山坡进行改造。经地质人员勘测,当坡角不超过45°时,可确保山体不滑坡,改造时保持坡脚A不动,从坡顶B沿BC削进到E处,问BE至少是多少米(结果保留根号)?
G
F
分析:就是当∠EAD=45°时,求BE的长,作BF⊥AD,EG⊥AD,则BE=GF=AG-AF。
典型例题
过点B作BF⊥AD,在Rt△ABF中,AB=40,∠BAD=60°,
过点E作EG⊥AD,在Rt△ABF中,GE=BF
当∠EAD=45°时,
点评:题目中没有直角三角形时,我们可以作辅助线构造直角三角形,作辅助线时要考虑如何充分和便利的使用已知条件。
G
F
解:
6.直角三角形纸片的两直角边分别BC为6,AC为8,现将△ABC,按如图折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是 。
A
B
C
6
8
E
D
方法点拨:设CE=x,则AE=BE=8-x,利用勾股定理求出x,再求tan∠CBE的值。
及时反馈
及时反馈
7.如图,某数学兴趣小组在活动课上测量学校旗杆高度。已知小明的眼睛与地面的距离是1.7m,看旗杆顶部的仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,看旗杆顶部的仰角为30°。两人相距28米且位于旗杆两侧(点B,N,D在同一条直线上)。请求出旗杆MN的高度。(结果保留整数)
MN=12米
8.如图,甲船在港口P的北偏西60°方向,距港口80海里的A处,沿AP方向以12海里/时的速度驶向港口P。乙船从港口P出发,沿北偏东45°方向匀速驶离港口P,现两船同时出发,2小时后乙船在甲船的正东方向,求乙船的航行速度。
及时反馈
谢 谢
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
