19.1.3平行四边形的判定(1)
文档属性
| 名称 | 19.1.3平行四边形的判定(1) |
|
|
| 格式 | zip | ||
| 文件大小 | 22.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-06-07 00:00:00 | ||
图片预览

文档简介
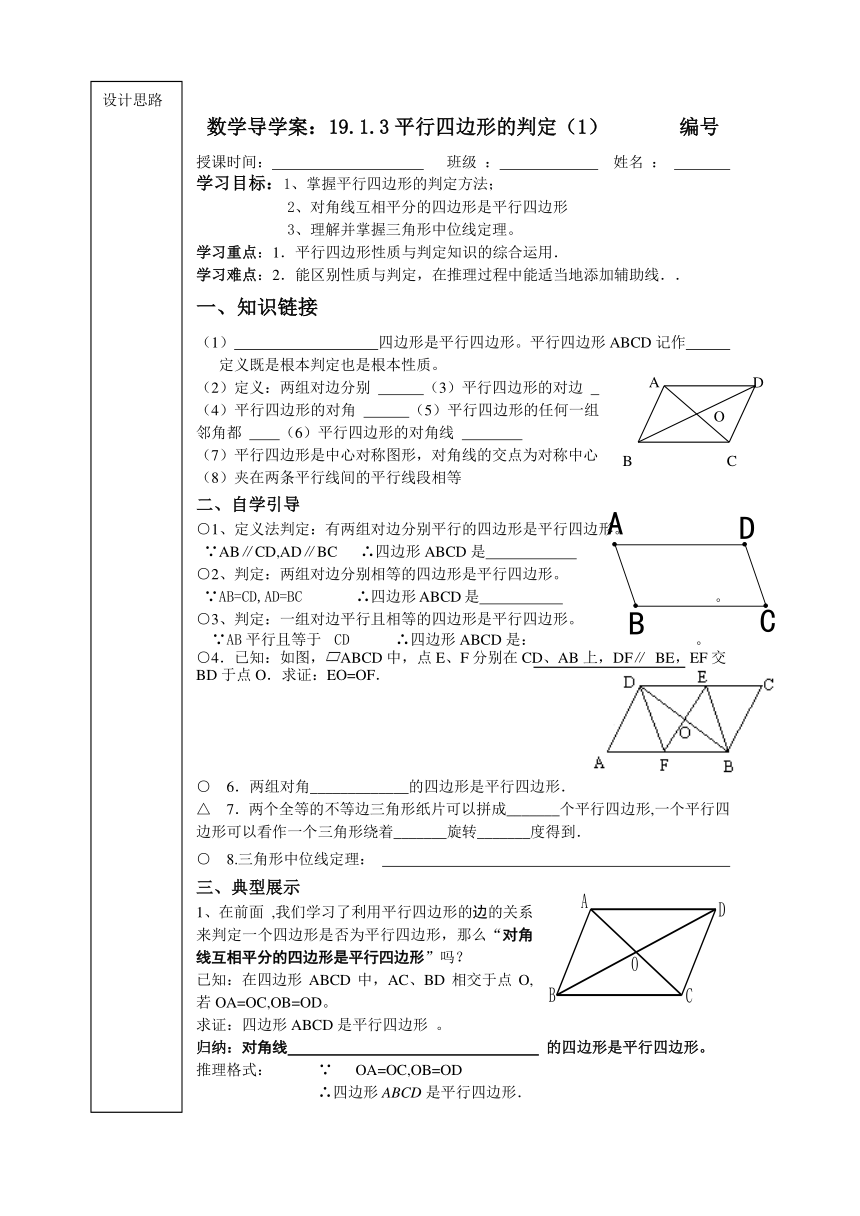
数学导学案:19.1.3平行四边形的判定(1) 编号
授课时间: 班级 : 姓名 :
学习目标:1、掌握平行四边形的判定方法;
2、对角线互相平分的四边形是平行四边形
3、理解并掌握三角形中位线定理。
学习重点:1.平行四边形性质与判定知识的综合运用.
学习难点:2.能区别性质与判定,在推理过程中能适当地添加辅助线..
一、知识链接
(1) 四边形是平行四边形。平行四边形ABCD记作
定义既是根本判定也是根本性质。
(2)定义:两组对边分别 (3)平行四边形的对边
(4)平行四边形的对角 (5)平行四边形的任何一组邻角都 (6)平行四边形的对角线
(7)平行四边形是中心对称图形,对角线的交点为对称中心
(8)夹在两条平行线间的平行线段相等
二、自学引导
○1、定义法判定:有两组对边分别平行的四边形是平行四边形。
∵AB∥CD,AD∥BC ∴四边形ABCD是
○2、判定:两组对边分别相等的四边形是平行四边形。
∵AB=CD,AD=BC ∴四边形ABCD是 。
○3、判定:一组对边平行且相等的四边形是平行四边形。
∵AB平行且等于CD ∴四边形ABCD是: 。
○4.已知:如图,ABCD中,点E、F分别在CD、AB上,DF∥ BE,EF交BD于点O.求证:EO=OF.
○ 6.两组对角_____________的四边形是平行四边形.
△ 7.两个全等的不等边三角形纸片可以拼成_______个平行四边形,一个平行四边形可以看作一个三角形绕着_______旋转_______度得到.
○ 8.三角形中位线定理:
三、典型展示
1、在前面 ,我们学习了利用平行四边形的边的关系来判定一个四边形是否为平行四边形,那么“对角线互相平分的四边形是平行四边形”吗?
已知:在四边形ABCD中,AC、BD相交于点O,若OA=OC,OB=OD。
求证:四边形ABCD是平行四边形 。
归纳:对角线 的四边形是平行四边形。
推理格式: ∵ OA=OC,OB=OD
∴四边形ABCD是平行四边形.
2、已知:如图ABCD的对角线AC、BD交于点O,E、F是AC上的两点,
并且AE=CF.
求证:四边形BFDE是平行四边形.
证明:
3、如图,在□ABCD中,BD为对角线,E、F分别是AD.BD的中点,连接EF.若EF=3,则CD的长为 .
四、我的收获
1. 我的收获:
2.疑问解决:
五、练习巩固
1、如图,四边形ABCD,AC、BD相交于点O,若OA=OC,OB=OD,则ABCD是__________,根据是_____________________
2.如图,在ABCD中,AC、BD相交于点O,若AC=10cm,BD=8cm,
那么当AO=__ _cm,DO=_ __cm时,ABCD为平行四边形.
3、在 ABCD中,两条对角线AC、BD相交于点O,如图与△ABO面积相等的三角形有( )个。A、1 B、2 C、3 D、4
4、如上图,在 ABCD中,对角线AC与BD交于O点,已知点E、F分别是
BD上的点,请你添加一个件 ,
使得AFCE是一个平行四边形。
六、课后作业
1、判断题:
(1)对角线相等的四边形是平行四边形 ( )
(2)对角线互相平分的四边形是平行四边形 ( )
2、在四边形ABCD中,AC交BD 于点O,若AO=1/2AC,BO=1/2BD,则四边形 ABCD 是平行四边形。( )
3、下列条件中能判断四边形是平行四边形的是( ).
A、对角线互相垂直 B、对角线相等
C对角线互相垂直且相等 D对角线互相平分
4、已知:在平行四边形ABCD中,对角线AC 、BD相交于点,M 、 N 、 P、 Q分别是OA 、OB 、OC 、 OD的中点。
求证 : 四边形MNPQ是平行四边形
设计思路
A
D
C
B
O
设计思路
授课时间: 班级 : 姓名 :
学习目标:1、掌握平行四边形的判定方法;
2、对角线互相平分的四边形是平行四边形
3、理解并掌握三角形中位线定理。
学习重点:1.平行四边形性质与判定知识的综合运用.
学习难点:2.能区别性质与判定,在推理过程中能适当地添加辅助线..
一、知识链接
(1) 四边形是平行四边形。平行四边形ABCD记作
定义既是根本判定也是根本性质。
(2)定义:两组对边分别 (3)平行四边形的对边
(4)平行四边形的对角 (5)平行四边形的任何一组邻角都 (6)平行四边形的对角线
(7)平行四边形是中心对称图形,对角线的交点为对称中心
(8)夹在两条平行线间的平行线段相等
二、自学引导
○1、定义法判定:有两组对边分别平行的四边形是平行四边形。
∵AB∥CD,AD∥BC ∴四边形ABCD是
○2、判定:两组对边分别相等的四边形是平行四边形。
∵AB=CD,AD=BC ∴四边形ABCD是 。
○3、判定:一组对边平行且相等的四边形是平行四边形。
∵AB平行且等于CD ∴四边形ABCD是: 。
○4.已知:如图,ABCD中,点E、F分别在CD、AB上,DF∥ BE,EF交BD于点O.求证:EO=OF.
○ 6.两组对角_____________的四边形是平行四边形.
△ 7.两个全等的不等边三角形纸片可以拼成_______个平行四边形,一个平行四边形可以看作一个三角形绕着_______旋转_______度得到.
○ 8.三角形中位线定理:
三、典型展示
1、在前面 ,我们学习了利用平行四边形的边的关系来判定一个四边形是否为平行四边形,那么“对角线互相平分的四边形是平行四边形”吗?
已知:在四边形ABCD中,AC、BD相交于点O,若OA=OC,OB=OD。
求证:四边形ABCD是平行四边形 。
归纳:对角线 的四边形是平行四边形。
推理格式: ∵ OA=OC,OB=OD
∴四边形ABCD是平行四边形.
2、已知:如图ABCD的对角线AC、BD交于点O,E、F是AC上的两点,
并且AE=CF.
求证:四边形BFDE是平行四边形.
证明:
3、如图,在□ABCD中,BD为对角线,E、F分别是AD.BD的中点,连接EF.若EF=3,则CD的长为 .
四、我的收获
1. 我的收获:
2.疑问解决:
五、练习巩固
1、如图,四边形ABCD,AC、BD相交于点O,若OA=OC,OB=OD,则ABCD是__________,根据是_____________________
2.如图,在ABCD中,AC、BD相交于点O,若AC=10cm,BD=8cm,
那么当AO=__ _cm,DO=_ __cm时,ABCD为平行四边形.
3、在 ABCD中,两条对角线AC、BD相交于点O,如图与△ABO面积相等的三角形有( )个。A、1 B、2 C、3 D、4
4、如上图,在 ABCD中,对角线AC与BD交于O点,已知点E、F分别是
BD上的点,请你添加一个件 ,
使得AFCE是一个平行四边形。
六、课后作业
1、判断题:
(1)对角线相等的四边形是平行四边形 ( )
(2)对角线互相平分的四边形是平行四边形 ( )
2、在四边形ABCD中,AC交BD 于点O,若AO=1/2AC,BO=1/2BD,则四边形 ABCD 是平行四边形。( )
3、下列条件中能判断四边形是平行四边形的是( ).
A、对角线互相垂直 B、对角线相等
C对角线互相垂直且相等 D对角线互相平分
4、已知:在平行四边形ABCD中,对角线AC 、BD相交于点,M 、 N 、 P、 Q分别是OA 、OB 、OC 、 OD的中点。
求证 : 四边形MNPQ是平行四边形
设计思路
A
D
C
B
O
设计思路
