江苏省南通市通州区2019-2020学年高一下学期期末学业质量监测数学试题 Word版含答案
文档属性
| 名称 | 江苏省南通市通州区2019-2020学年高一下学期期末学业质量监测数学试题 Word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-16 00:00:00 | ||
图片预览




文档简介
11633200106426002019—2020学年末学业质量监测试卷
高一数学
一、选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知false是单位向量,且false,则false=
false
2. 在△ABC中,若sinA:sin B:sinC=3:5:7,则C=
А. 30°
B. 60°
C. 120°
D. 150°
3.使式子false有意义的x的取值范围是
false
4.已知角α的终边为false,则false
false
5. 设集合false,则A∩8中的元素个数为
A. 0
B. 1
C. 2
D. 3
6. 我国古代典籍《周易》中用“卦”描述万物的变化,每一“重卦”由从上到下排列的6个爻组成,爻分为阳爻“——”和阴爻“一 一”,如图就是一个重卦,已知某重卦从上到下排列的前3个爻均为阴爻,若后3个爻随机产生,则该重卦恰含2个阳爻的概率为
32956500false
7. 已知球O的表面积为16π,球心O到球内一点P的距离为1,则过点P的截面的面积的最小值为
A. 3π
B. 4π
C. 6π
D. 8π
8. 设直线l过点P(1, 2),在两坐标轴上的截距的绝对值相等,则满足题设的直线l的条数为
A. 1
В. 2
C. 3
D.4
二、选择题:本大题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得3分。
9. 某篮球运动员8场比赛中罚球次数的统计数据分别为: 2, 6, 8, 3, 3, 4, 6, 8,关于该组数据,下列说法正确的是
A.中位数为3
B.众数为3, 6, 8
C.平均数为5
D.方差为4.8
10.设a, b均为正数,且a+2b=1,则下列结论正确的是
A. ab有最大值
B. false有最大值
C. false有最小值
D.false有最小值false
38544508890011.在棱长为1的正方体false中,下列结论正确的是
A.异面直线BD1与B1C所成的角大小为90°
B.四面体D1DBC的每个面都是直角三角形
C.二面角false的大小为30°
D.正方体false的内切球上一点与外接球上一点的距离的最小值为false
12.某同学在研究函数false的性质时,联想到两点间的距离公式,从而将函数变形为false,则下列结论正确的是
A.函数f(x)在区间(-,0)上单调递减, (1,+)上单调递增
B.函数f(x)的最小值为,没有最大值
C.存在实数t,使得函数f(x)的图象关于直线x=t对称
D.方程f(x)=2的实根个数为2
三、填空题:本大题共4小题,每小题5分,共20分。
13.在空间中,已知直线l,两个不同的平面α,β,下列三个条件中,一定能推出"α∥β "的条件序号是________
false
14.圆false与圆false的公切线共有________条.
15.函数false的图象上一点到坐标原点的距离的平方的最小值为________.
4997450016.某地积极创建全国文明城市,考虑环保和美观,为城区街道统一换置了新型垃圾桶(如图) ,已知该垃圾桶由上、下两部分组成(上部为多面体,下部为长方体,高度比为1:2),垃圾桶最上面是正方形,与之相邻的四个面都是全等三角形,垃圾投入口是边长为a的正六边形,该垃圾桶下部长方体的容积为________,该垃圾桶的顶部面积(最上面正方形及与之相邻的四个三角形的面积之和)为________ (本题第一空2分,第二空3分)
四、解答题:本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17. (本小题满分10分)
在false这三个条件中选择两个,补充在下面问题中,使得△ABC存在且唯一,并解答补充完整后的问题.
问题:在△ABC中,已知内角A, B, C的对边分别为a, b, c,且false,________,________,求△ABC的面积.
注:如果选择多种条件分别解答,按第一种解答计分.
18. (本小题满分12分)
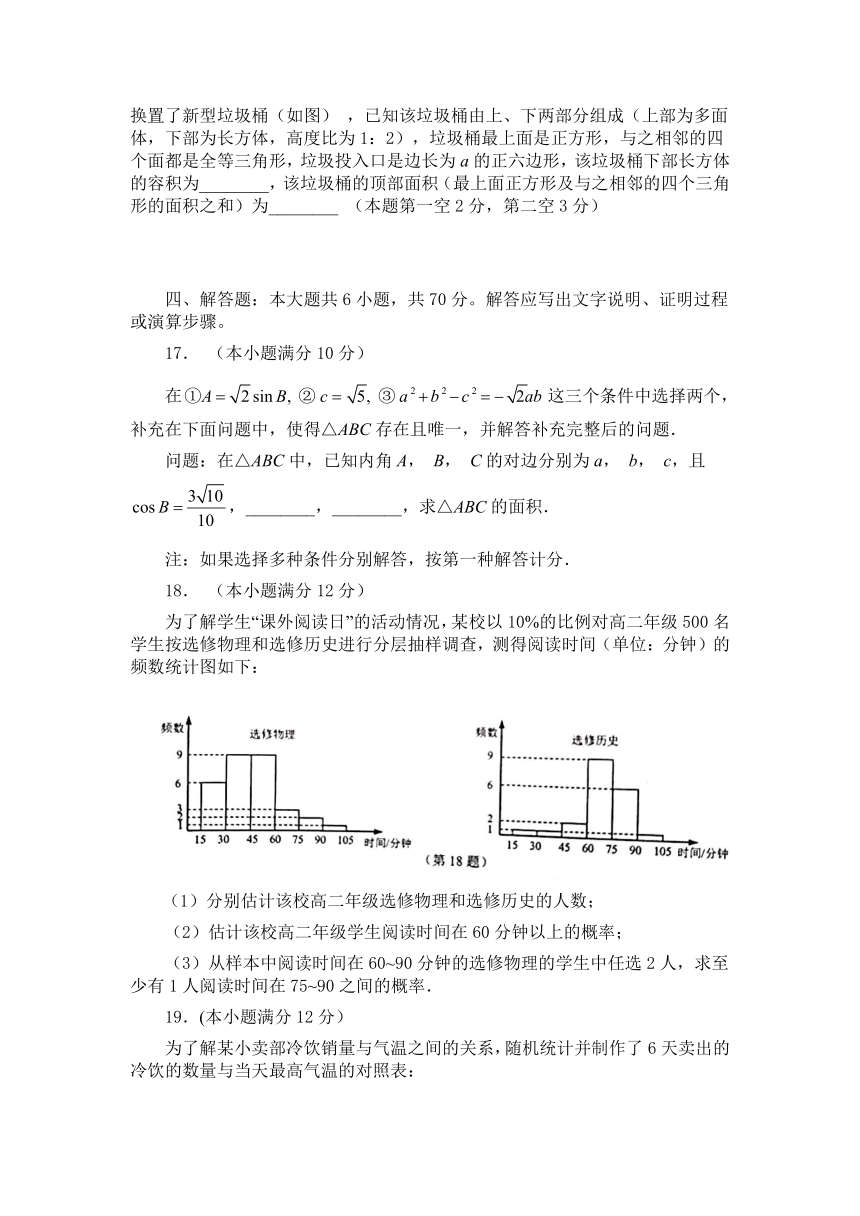
为了解学生“课外阅读日”的活动情况,某校以10%的比例对高二年级500名学生按选修物理和选修历史进行分层抽样调查,测得阅读时间(单位:分钟)的频数统计图如下:
(1)分别估计该校高二年级选修物理和选修历史的人数;
(2)估计该校高二年级学生阅读时间在60分钟以上的概率;
(3)从样本中阅读时间在60~90分钟的选修物理的学生中任选2人,求至少有1人阅读时间在75~90之间的概率.
19.(本小题满分12分)
为了解某小卖部冷饮销量与气温之间的关系,随机统计并制作了6天卖出的冷饮的数量与当天最高气温的对照表:
(1)画出散点图,并求出y关于x的线性回归方程;
3702050340360(2)根据天气预报,某天最高气温为36.6℃,请你根据这些数据预测这天小卖部卖出的冷饮数量.
附:一组数据false的
回归直线y=a+bx的斜率和截距的最小二乘估计为false
20. (本小题满分12分)
如图,已知四棱锥P-ABCD中,底面ABCD为直角梯形, AD∥BC,
3067050485140∠BAD=90°,且AB=BC=1, AD=2, PA=PD,点M为AD中点 ,平面PAD⊥平面ABCD,直线PB与平面ABCD所成角的正切值为false.
(1)求证: BM∥平面PCD;
(2)求四棱锥P—ABCD的体积;
(3)用一个平面去截四棱锥P—ABCD,请作出一个平行四边形截面(无须证明),并写出你能作出的平行四边形截面的个数.
21. (本小题满分12分)
在平面直角坐标系xOy中,已知圆C的圆心在直线false上,且圆心的横坐标为整数,圆C被x轴截得的弦长为8, 点M (7, 7)在圆C上.
(1)求圆C的方程;
(2)已知直线l的斜率为,在y轴上的截距t(t为常数),与圆C相交于点A, B.问:直线OA, OB是否关于x轴对称?若对称,请证明;若不对称,请说明理由.
22. (本小题满分12分)
已知函数false.
(1)若false,求a的值
(2)若函数f(x)的图象在x轴的上方,求a的取值范围.
高一数学
一、选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知false是单位向量,且false,则false=
false
2. 在△ABC中,若sinA:sin B:sinC=3:5:7,则C=
А. 30°
B. 60°
C. 120°
D. 150°
3.使式子false有意义的x的取值范围是
false
4.已知角α的终边为false,则false
false
5. 设集合false,则A∩8中的元素个数为
A. 0
B. 1
C. 2
D. 3
6. 我国古代典籍《周易》中用“卦”描述万物的变化,每一“重卦”由从上到下排列的6个爻组成,爻分为阳爻“——”和阴爻“一 一”,如图就是一个重卦,已知某重卦从上到下排列的前3个爻均为阴爻,若后3个爻随机产生,则该重卦恰含2个阳爻的概率为
32956500false
7. 已知球O的表面积为16π,球心O到球内一点P的距离为1,则过点P的截面的面积的最小值为
A. 3π
B. 4π
C. 6π
D. 8π
8. 设直线l过点P(1, 2),在两坐标轴上的截距的绝对值相等,则满足题设的直线l的条数为
A. 1
В. 2
C. 3
D.4
二、选择题:本大题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得3分。
9. 某篮球运动员8场比赛中罚球次数的统计数据分别为: 2, 6, 8, 3, 3, 4, 6, 8,关于该组数据,下列说法正确的是
A.中位数为3
B.众数为3, 6, 8
C.平均数为5
D.方差为4.8
10.设a, b均为正数,且a+2b=1,则下列结论正确的是
A. ab有最大值
B. false有最大值
C. false有最小值
D.false有最小值false
38544508890011.在棱长为1的正方体false中,下列结论正确的是
A.异面直线BD1与B1C所成的角大小为90°
B.四面体D1DBC的每个面都是直角三角形
C.二面角false的大小为30°
D.正方体false的内切球上一点与外接球上一点的距离的最小值为false
12.某同学在研究函数false的性质时,联想到两点间的距离公式,从而将函数变形为false,则下列结论正确的是
A.函数f(x)在区间(-,0)上单调递减, (1,+)上单调递增
B.函数f(x)的最小值为,没有最大值
C.存在实数t,使得函数f(x)的图象关于直线x=t对称
D.方程f(x)=2的实根个数为2
三、填空题:本大题共4小题,每小题5分,共20分。
13.在空间中,已知直线l,两个不同的平面α,β,下列三个条件中,一定能推出"α∥β "的条件序号是________
false
14.圆false与圆false的公切线共有________条.
15.函数false的图象上一点到坐标原点的距离的平方的最小值为________.
4997450016.某地积极创建全国文明城市,考虑环保和美观,为城区街道统一换置了新型垃圾桶(如图) ,已知该垃圾桶由上、下两部分组成(上部为多面体,下部为长方体,高度比为1:2),垃圾桶最上面是正方形,与之相邻的四个面都是全等三角形,垃圾投入口是边长为a的正六边形,该垃圾桶下部长方体的容积为________,该垃圾桶的顶部面积(最上面正方形及与之相邻的四个三角形的面积之和)为________ (本题第一空2分,第二空3分)
四、解答题:本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17. (本小题满分10分)
在false这三个条件中选择两个,补充在下面问题中,使得△ABC存在且唯一,并解答补充完整后的问题.
问题:在△ABC中,已知内角A, B, C的对边分别为a, b, c,且false,________,________,求△ABC的面积.
注:如果选择多种条件分别解答,按第一种解答计分.
18. (本小题满分12分)
为了解学生“课外阅读日”的活动情况,某校以10%的比例对高二年级500名学生按选修物理和选修历史进行分层抽样调查,测得阅读时间(单位:分钟)的频数统计图如下:
(1)分别估计该校高二年级选修物理和选修历史的人数;
(2)估计该校高二年级学生阅读时间在60分钟以上的概率;
(3)从样本中阅读时间在60~90分钟的选修物理的学生中任选2人,求至少有1人阅读时间在75~90之间的概率.
19.(本小题满分12分)
为了解某小卖部冷饮销量与气温之间的关系,随机统计并制作了6天卖出的冷饮的数量与当天最高气温的对照表:
(1)画出散点图,并求出y关于x的线性回归方程;
3702050340360(2)根据天气预报,某天最高气温为36.6℃,请你根据这些数据预测这天小卖部卖出的冷饮数量.
附:一组数据false的
回归直线y=a+bx的斜率和截距的最小二乘估计为false
20. (本小题满分12分)
如图,已知四棱锥P-ABCD中,底面ABCD为直角梯形, AD∥BC,
3067050485140∠BAD=90°,且AB=BC=1, AD=2, PA=PD,点M为AD中点 ,平面PAD⊥平面ABCD,直线PB与平面ABCD所成角的正切值为false.
(1)求证: BM∥平面PCD;
(2)求四棱锥P—ABCD的体积;
(3)用一个平面去截四棱锥P—ABCD,请作出一个平行四边形截面(无须证明),并写出你能作出的平行四边形截面的个数.
21. (本小题满分12分)
在平面直角坐标系xOy中,已知圆C的圆心在直线false上,且圆心的横坐标为整数,圆C被x轴截得的弦长为8, 点M (7, 7)在圆C上.
(1)求圆C的方程;
(2)已知直线l的斜率为,在y轴上的截距t(t为常数),与圆C相交于点A, B.问:直线OA, OB是否关于x轴对称?若对称,请证明;若不对称,请说明理由.
22. (本小题满分12分)
已知函数false.
(1)若false,求a的值
(2)若函数f(x)的图象在x轴的上方,求a的取值范围.
同课章节目录
