江苏省无锡市2019-2020学年高一下学期期末调研考试数学试题 Word版含答案
文档属性
| 名称 | 江苏省无锡市2019-2020学年高一下学期期末调研考试数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 717.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-16 20:42:36 | ||
图片预览



文档简介
1266190012560300无锡市普通高中2020年春学期高一期终调研考试试卷
数学
2020.7
公式参考:
线性回归方程false,其中false.
一、单项选择题:(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中只有一项是符合题目要求的。请将答案填写在答题卡相应位置上.)
1.用符号表示“点P在直线l上,直线l在平面α外”,正确的是(▲)
false
2.某医院治疗一种疾病的治愈率为50%,下列说法正确的是(▲)
A.如果第1位病人没有治愈,那么第2位病人一定能治愈
B.2位病人中一定有1位能治愈
C.每位病人治愈的可能性是50%
D.所有病人中一定有一半的人能治愈
3.直线x+2y+3=0在y轴上的截距为(▲)
false
4.某种产品的广告费支出x与销售额y之间有如下对应数据:
对上述数据进行分析,发现y与x之间具有线性相关关系,下列四个线性回归方程中正确的选项是(▲)
false
5.在空间直角坐标系中,已知△ABC的顶点分别为A(1,2,1),B(1,4,2),C(0,4,2),则△ABC的形状为(▲)
A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.等边三角形
6.某养路处有一圆锥形仓库用于储藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12米,高4米,为存放更多的食盐,养路处拟重建仓库,将其高度增加4米,底面直径不变,则新建仓库比原仓库能多储藏食盐的体积为(▲)
A.24π米3
B.48π米3
C.96π米3
421640082550D.192π米3
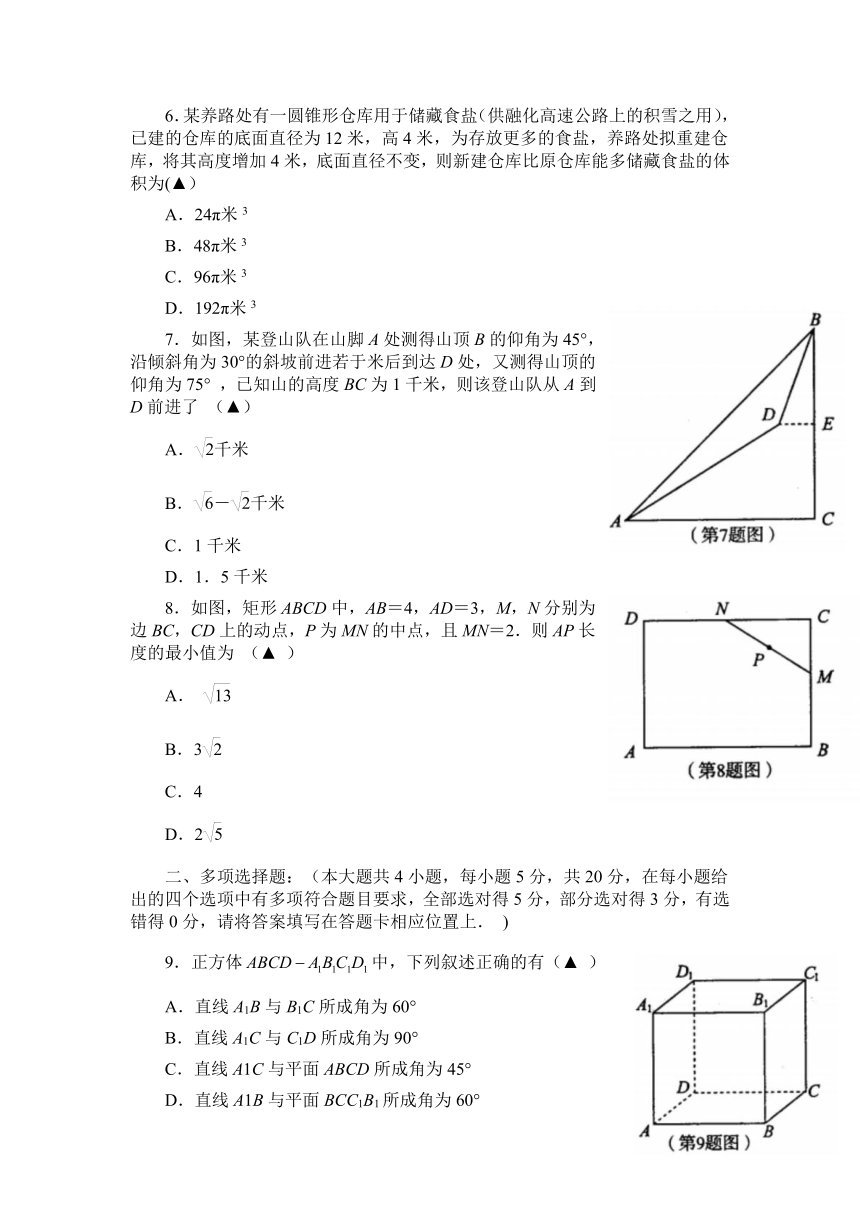
7.如图,某登山队在山脚A处测得山顶B的仰角为45°,沿倾斜角为30°的斜坡前进若于米后到达D处,又测得山顶的仰角为75° ,已知山的高度BC为1千米,则该登山队从A到D前进了 (▲)
A.千米
B.-千米
C.1千米
D.1.5千米
right50808.如图,矩形ABCD中,AB=4,AD=3,M,N分别为边BC,CD上的动点,P为MN的中点,且MN=2.则AP长度的最小值为 (▲ )
A.
B.3
C.4
D.2
二、多项选择题:(本大题共4小题,每小题5分,共20分,在每小题给出的四个选项中有多项符合题目要求,全部选对得5分,部分选对得3分,有选错得0分,请将答案填写在答题卡相应位置上. )
44323001174759.正方体false中,下列叙述正确的有(▲ )
A.直线A1B与B1C所成角为60°
B.直线A1C与C1D所成角为90°
C.直线A1C与平面ABCD所成角为45°
D.直线A1B与平面BCC1B1所成角为60°
10.已知一组数据false的平均数和方差均为2,则下列叙述正确的有(▲ )
A.false的平均数为3
B.false的方差为3
C.false的方差为4
D.false的方差为8
11.下列关于直线的斜率和倾斜角的叙述正确的有(▲ )
A.平面直角坐标系中的任意一条直线都有倾斜角
B.平面直角坐标系中的任意一条直线都有斜率
C.若一条直线的斜率为tanα,则该直线的倾斜角为α
D.若一条直线的倾斜角为α(α≠90°),则该直线的斜率为tanα
12.在△ABC中,已知角A,B,C所对的边分别为a,b,c,且false,则以下四个结论正确的有(▲ )
A. △ABC不可能是直角三角形
B. △ABC有可能是等边三角形
C.当A=B时,△ABC的周长为15
D.当B=时,△ABC的面积为6
三、填空题:(本大题共4小题,每小题5分,共计20分,请把答案填写在答题卡相应位置上.)
13.下表是关于某校高一年级男女生选科意向的调查数据,人数如表所示:
现要在所有参与调查的人中用分层抽样的方法抽取n个人做进一步的调查,若在“选修物理的男生”中抽取了8人,则n的值为________
14.若两条直线ax+2y+1=0和(a-1)x-ay-1=0互相垂直,则a的值为________
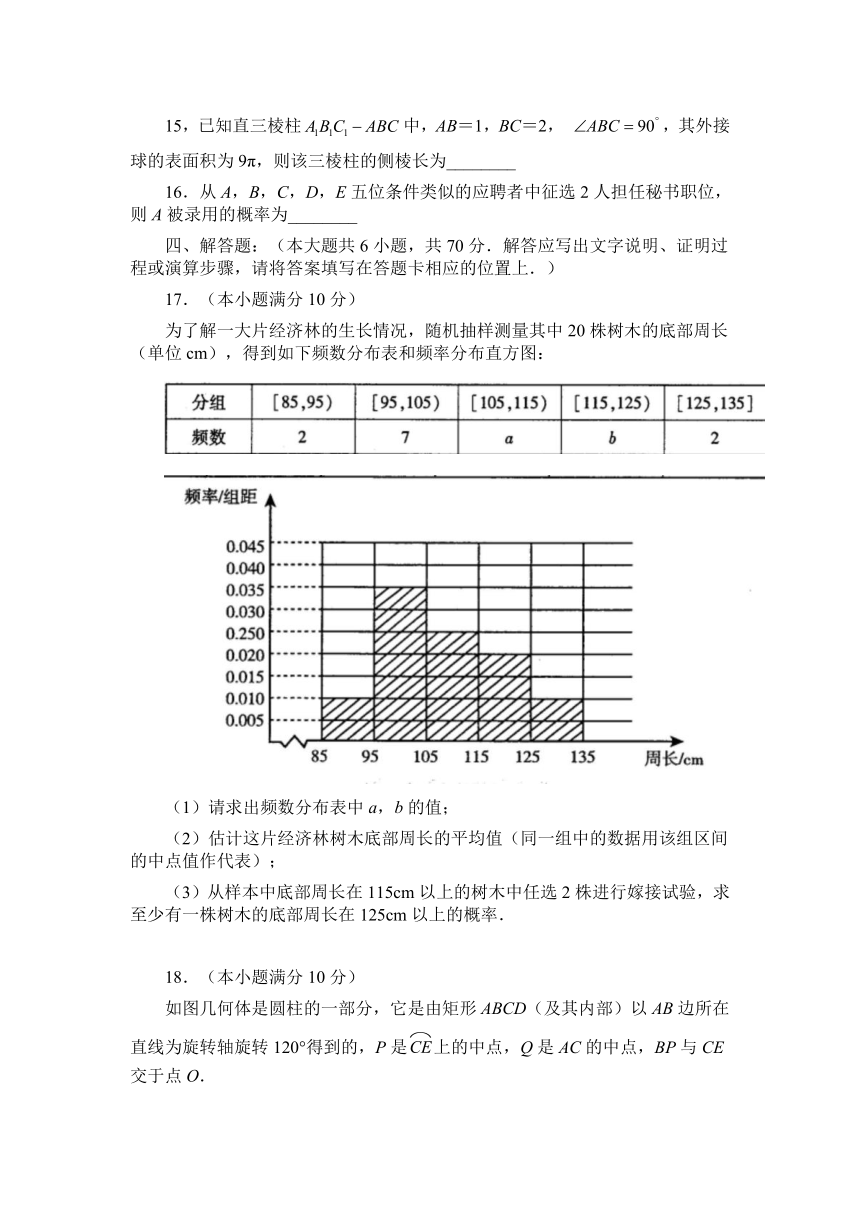
15,已知直三棱柱false中,AB=1,BC=2, false,其外接球的表面积为9π,则该三棱柱的侧棱长为________
16.从A,B,C,D,E五位条件类似的应聘者中征选2人担任秘书职位,则A被录用的概率为________
四、解答题:(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤,请将答案填写在答题卡相应的位置上.)
17.(本小题满分10分)
为了解一大片经济林的生长情况,随机抽样测量其中20株树木的底部周长(单位cm),得到如下频数分布表和频率分布直方图:
(1)请求出频数分布表中a,b的值;
(2)估计这片经济林树木底部周长的平均值(同一组中的数据用该组区间的中点值作代表);
(3)从样本中底部周长在115cm以上的树木中任选2株进行嫁接试验,求至少有一株树木的底部周长在125cm以上的概率.
18.(本小题满分10分)
如图几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,P是上的中点,Q是AC的中点,BP与CE交于点O.
46228000(1)求证:OQ∥平面ABEF;
(2)求证:AP⊥CE.
19. (本小题满分12分)
已知圆C过三点(1,3),(4,2),(1,-7).
(1)求圆C的方程;
(2)斜率为1的直线l与圆C交于M,N两点,若△CMN为等腰直角三角形,求直线l的方程
20. (本小题满分12分)
在△ABC中,已知tanA =2,tanB=3.
(1)若△ABC最小边的长为5,求△ABC最大边的长;
4933950365760(2)若AC边上的中线BD长为,求△ABC的面积.
21.(本小题满分12分)
如图,四棱锥P—ABCD中,底画ABCD是边长为2的正方形,侧面PBC为正三角形,M,N分别为PD,BC的中点,PN⊥AB.
(1)求三棱锥P-AMN的体积;
(2)求二面角M-AN-D的正切值.
22. (本小题满分14分)
已知圆Cfalse和圆D:false为圆D上动点。
(1)过点A作一条直线l,若l被圆C和圆D截得的弦长相等,求直线l的方程;
(2)求证:当点P不在x轴上时,总存在圆C上点M和圆D上点N,使得四边形AMPN为平行四边形.
无锡市普通高中2020年春学期期末测试答案解析
单项选择题
1-5:B C D A B
6-8:B C C
7解析:设,由正弦定理得:
选C
8解析:以false为false轴,以false为false轴建系:设
false
false
false
表示圆心到(-4,-3)距离最小得一半
false
选C
多项选择题
9.AB
10.AD
11.AD
12.CD
12解析:由正弦定理得false
false
false
false
false
填空题
13:20
14:0或3
15:2
false
15解析:将直三棱柱补形为长方体ABEC?A1B1E1C1,则球O是长方体ABEC?A1B1E1C1的外接球.
所以体对角线BC1的长为球O的直径.S球=4πR2=9π.所以半径R=false
设侧棱为x,2R=false3.解得侧棱为2
16解析:总数共10种,A被录用可能为AB、AC、AD、AE四种
解答题
17答案:(1)false
(2)108.5
(3)false
18解析:false
false
19解析:(1)圆心在y=-2上,设圆心坐标(x,-2),false
false
(2)false
false
false
false
20解析:(1)解:,∵,∴,∵,∴,
∴∴∴最大边为b,最小边为c
由正弦定理,得,∴,即最大边长为
法一:(2)解:由正弦定理得:a:b:c=sinA:sinB:sinC,设b=则
由余弦定理中线长定理:
得,解得,
得∴
法二:见切作高:作CE垂直AB,设
由中线长公式得
21.解析⑴ ∵PB=PC,∴PN⊥BC,又∵PN⊥AB,AB∩BD=B,AB、BCfalse,
∴PN⊥平面ABCD,∵AB=BC=PB=PC=2,∴PN=false,
∴false
⑵ 取DN中点E,连接ME,∵M、E为中点,∴ME∥PN,∵PN⊥平面ABCD,∴ME⊥平面ABCD
过E作EQ⊥AN,则MQ⊥AN,∠MQE即为该二面角的平面角,∴false
∵PN=false,∴false,∵false∴false,∴false
false即该二面角的正切值为false
22.解析:⑴设直线l:
false由弦长相等,得
false
false∴ l: y=4或8x+y-20=0
⑵设P(x0,y0),则
falsefalse设AM: ,则PN:
由弦长相等,得
false
false
false得:
falsefalse化为关于k的方程:
二次项系数
false
∴存在k使等式成立,即存在k使AMPN为平行四边形
数学
2020.7
公式参考:
线性回归方程false,其中false.
一、单项选择题:(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中只有一项是符合题目要求的。请将答案填写在答题卡相应位置上.)
1.用符号表示“点P在直线l上,直线l在平面α外”,正确的是(▲)
false
2.某医院治疗一种疾病的治愈率为50%,下列说法正确的是(▲)
A.如果第1位病人没有治愈,那么第2位病人一定能治愈
B.2位病人中一定有1位能治愈
C.每位病人治愈的可能性是50%
D.所有病人中一定有一半的人能治愈
3.直线x+2y+3=0在y轴上的截距为(▲)
false
4.某种产品的广告费支出x与销售额y之间有如下对应数据:
对上述数据进行分析,发现y与x之间具有线性相关关系,下列四个线性回归方程中正确的选项是(▲)
false
5.在空间直角坐标系中,已知△ABC的顶点分别为A(1,2,1),B(1,4,2),C(0,4,2),则△ABC的形状为(▲)
A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.等边三角形
6.某养路处有一圆锥形仓库用于储藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12米,高4米,为存放更多的食盐,养路处拟重建仓库,将其高度增加4米,底面直径不变,则新建仓库比原仓库能多储藏食盐的体积为(▲)
A.24π米3
B.48π米3
C.96π米3
421640082550D.192π米3
7.如图,某登山队在山脚A处测得山顶B的仰角为45°,沿倾斜角为30°的斜坡前进若于米后到达D处,又测得山顶的仰角为75° ,已知山的高度BC为1千米,则该登山队从A到D前进了 (▲)
A.千米
B.-千米
C.1千米
D.1.5千米
right50808.如图,矩形ABCD中,AB=4,AD=3,M,N分别为边BC,CD上的动点,P为MN的中点,且MN=2.则AP长度的最小值为 (▲ )
A.
B.3
C.4
D.2
二、多项选择题:(本大题共4小题,每小题5分,共20分,在每小题给出的四个选项中有多项符合题目要求,全部选对得5分,部分选对得3分,有选错得0分,请将答案填写在答题卡相应位置上. )
44323001174759.正方体false中,下列叙述正确的有(▲ )
A.直线A1B与B1C所成角为60°
B.直线A1C与C1D所成角为90°
C.直线A1C与平面ABCD所成角为45°
D.直线A1B与平面BCC1B1所成角为60°
10.已知一组数据false的平均数和方差均为2,则下列叙述正确的有(▲ )
A.false的平均数为3
B.false的方差为3
C.false的方差为4
D.false的方差为8
11.下列关于直线的斜率和倾斜角的叙述正确的有(▲ )
A.平面直角坐标系中的任意一条直线都有倾斜角
B.平面直角坐标系中的任意一条直线都有斜率
C.若一条直线的斜率为tanα,则该直线的倾斜角为α
D.若一条直线的倾斜角为α(α≠90°),则该直线的斜率为tanα
12.在△ABC中,已知角A,B,C所对的边分别为a,b,c,且false,则以下四个结论正确的有(▲ )
A. △ABC不可能是直角三角形
B. △ABC有可能是等边三角形
C.当A=B时,△ABC的周长为15
D.当B=时,△ABC的面积为6
三、填空题:(本大题共4小题,每小题5分,共计20分,请把答案填写在答题卡相应位置上.)
13.下表是关于某校高一年级男女生选科意向的调查数据,人数如表所示:
现要在所有参与调查的人中用分层抽样的方法抽取n个人做进一步的调查,若在“选修物理的男生”中抽取了8人,则n的值为________
14.若两条直线ax+2y+1=0和(a-1)x-ay-1=0互相垂直,则a的值为________
15,已知直三棱柱false中,AB=1,BC=2, false,其外接球的表面积为9π,则该三棱柱的侧棱长为________
16.从A,B,C,D,E五位条件类似的应聘者中征选2人担任秘书职位,则A被录用的概率为________
四、解答题:(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤,请将答案填写在答题卡相应的位置上.)
17.(本小题满分10分)
为了解一大片经济林的生长情况,随机抽样测量其中20株树木的底部周长(单位cm),得到如下频数分布表和频率分布直方图:
(1)请求出频数分布表中a,b的值;
(2)估计这片经济林树木底部周长的平均值(同一组中的数据用该组区间的中点值作代表);
(3)从样本中底部周长在115cm以上的树木中任选2株进行嫁接试验,求至少有一株树木的底部周长在125cm以上的概率.
18.(本小题满分10分)
如图几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,P是上的中点,Q是AC的中点,BP与CE交于点O.
46228000(1)求证:OQ∥平面ABEF;
(2)求证:AP⊥CE.
19. (本小题满分12分)
已知圆C过三点(1,3),(4,2),(1,-7).
(1)求圆C的方程;
(2)斜率为1的直线l与圆C交于M,N两点,若△CMN为等腰直角三角形,求直线l的方程
20. (本小题满分12分)
在△ABC中,已知tanA =2,tanB=3.
(1)若△ABC最小边的长为5,求△ABC最大边的长;
4933950365760(2)若AC边上的中线BD长为,求△ABC的面积.
21.(本小题满分12分)
如图,四棱锥P—ABCD中,底画ABCD是边长为2的正方形,侧面PBC为正三角形,M,N分别为PD,BC的中点,PN⊥AB.
(1)求三棱锥P-AMN的体积;
(2)求二面角M-AN-D的正切值.
22. (本小题满分14分)
已知圆Cfalse和圆D:false为圆D上动点。
(1)过点A作一条直线l,若l被圆C和圆D截得的弦长相等,求直线l的方程;
(2)求证:当点P不在x轴上时,总存在圆C上点M和圆D上点N,使得四边形AMPN为平行四边形.
无锡市普通高中2020年春学期期末测试答案解析
单项选择题
1-5:B C D A B
6-8:B C C
7解析:设,由正弦定理得:
选C
8解析:以false为false轴,以false为false轴建系:设
false
false
false
表示圆心到(-4,-3)距离最小得一半
false
选C
多项选择题
9.AB
10.AD
11.AD
12.CD
12解析:由正弦定理得false
false
false
false
false
填空题
13:20
14:0或3
15:2
false
15解析:将直三棱柱补形为长方体ABEC?A1B1E1C1,则球O是长方体ABEC?A1B1E1C1的外接球.
所以体对角线BC1的长为球O的直径.S球=4πR2=9π.所以半径R=false
设侧棱为x,2R=false3.解得侧棱为2
16解析:总数共10种,A被录用可能为AB、AC、AD、AE四种
解答题
17答案:(1)false
(2)108.5
(3)false
18解析:false
false
19解析:(1)圆心在y=-2上,设圆心坐标(x,-2),false
false
(2)false
false
false
false
20解析:(1)解:,∵,∴,∵,∴,
∴∴∴最大边为b,最小边为c
由正弦定理,得,∴,即最大边长为
法一:(2)解:由正弦定理得:a:b:c=sinA:sinB:sinC,设b=则
由余弦定理中线长定理:
得,解得,
得∴
法二:见切作高:作CE垂直AB,设
由中线长公式得
21.解析⑴ ∵PB=PC,∴PN⊥BC,又∵PN⊥AB,AB∩BD=B,AB、BCfalse,
∴PN⊥平面ABCD,∵AB=BC=PB=PC=2,∴PN=false,
∴false
⑵ 取DN中点E,连接ME,∵M、E为中点,∴ME∥PN,∵PN⊥平面ABCD,∴ME⊥平面ABCD
过E作EQ⊥AN,则MQ⊥AN,∠MQE即为该二面角的平面角,∴false
∵PN=false,∴false,∵false∴false,∴false
false即该二面角的正切值为false
22.解析:⑴设直线l:
false由弦长相等,得
false
false∴ l: y=4或8x+y-20=0
⑵设P(x0,y0),则
falsefalse设AM: ,则PN:
由弦长相等,得
false
false
false得:
falsefalse化为关于k的方程:
二次项系数
false
∴存在k使等式成立,即存在k使AMPN为平行四边形
同课章节目录
