人教版数学八年级上册 11.1.1 三角形的边 课件(25张)
文档属性
| 名称 | 人教版数学八年级上册 11.1.1 三角形的边 课件(25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 444.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-17 06:57:44 | ||
图片预览






文档简介
(共25张PPT)
11.1.1三角形的边
——三角形的有关概念、分类及三边关系
第十一章
三角形
三角形是我们早已熟悉的图形,你能列举出日常生活中形如三角形的物体吗?对于三角形,你了解了哪些方面的知识?你能画一个三角形吗?
新课导入
学习目标:
1.记住三角形的有关概念.
2.会用符号表示三角形,会对三角形进行分类.
3.能说出三角形的三边关系,并能运用三角形
三边关系解决相关问题.
学习重、难点:
重点:三角形及其有关的概念;三角形的分类.
难点:三角形三边关系及应用.
推进新课
理解三角形的有关概念
问题1
三角形是我们熟悉的图形,观察下列图片,你能说一说三角形是怎样的图形吗?
知识点1
边:AB,BC,AC
或
c,a,b.
顶点:点A,B,C
.
内角:∠A
,∠B
,∠C.
追问:对于教科书图11.1-1中的三角形,你能说出它的边、顶点与内角吗?
A
B
C
a
b
c
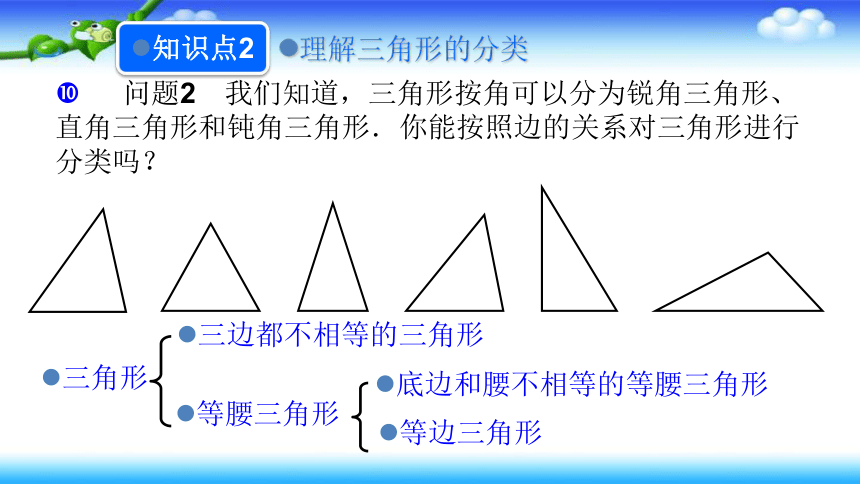
问题2
我们知道,三角形按角可以分为锐角三角形、直角三角形和钝角三角形.你能按照边的关系对三角形进行分类吗?
三边都不相等的三角形
三角形
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
理解三角形的分类
知识点2
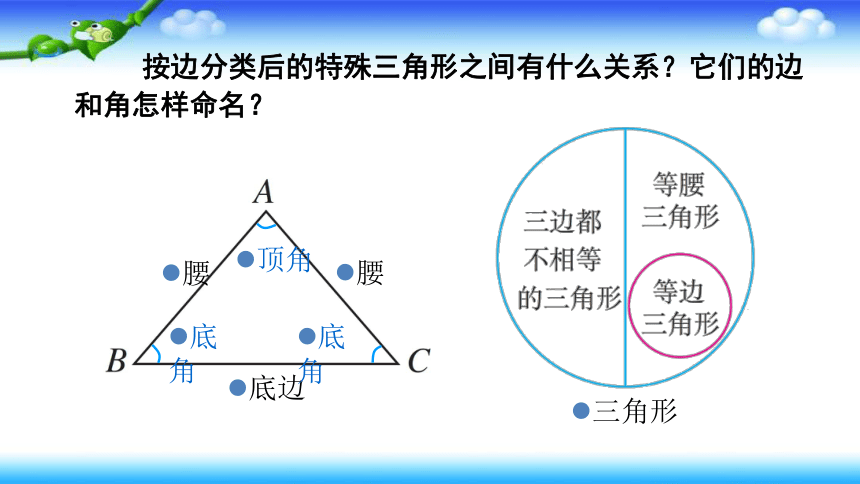
按边分类后的特殊三角形之间有什么关系?它们的边和角怎样命名?
腰
腰
底边
三角形
顶角
底角
底角
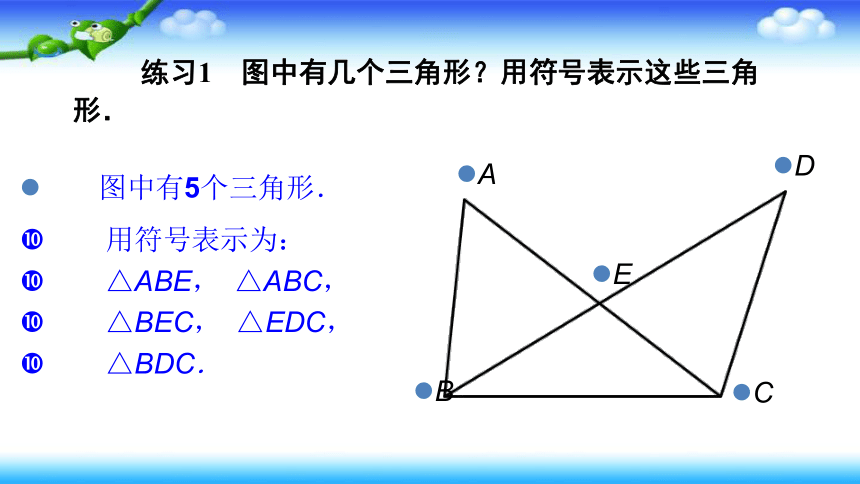
图中有5个三角形.
用符号表示为:
△ABE,
△ABC,
△BEC,
△EDC,
△BDC.
练习1 图中有几个三角形?用符号表示这些三角形.
A
B
C
D
E
(4)
练习2 下列说法正确的有_______.
(1)锐角三角形是三条边都不相等的三角形;
(2)直角三角形不是等腰三角形;
(3)等腰三角形是等边三角形;
(4)等边三角形是等腰三角形.
△ABC,△AEC,△ADC
练习3 如图,共有6个三角形,其中以AC为边的三角形是_________________________;以∠B为内角的三角形有_________________________.
△ABC,△DBC,△EBC
AB
+
AC
>BC,
①
AC
+
BC
>AB,
②
AB
+
BC
>AC.
③
即三角形两边的和大于第三边.
问题3
如图,任意画一个△ABC,一只小虫从点B
出发,沿三角形的边爬到点C,它有几条路线可以选择?各条线路的长一样吗?你能运用所学知识解释你的发现吗?由此你能推出三条边之间有怎样的关系?
B
C
A
探索与证明三角形三边的关系
知识点3
三角形两边的差小于第三边.
由不等式②③移项可得
BC
>AB
-AC,
BC
>AC
-AB.由此你能得出什么结论?
B
C
A
解:(1)能.因为3
+
4>5,3
+
5>4,4
+
5>3,
符合三角形两边的和大于第三边.
(2)不能.因为5
+
6
=11,
不符合三角形两边的和大于第三边.
(3)能.因为5
+
6>10,10
+
6>5,10
+
5>6,
符合三角形两边的和大于第三边.
问题:下列长度的三条线段能否组成三角形?为什么?(1)3,4,5;(2)5,6,11;(3)5,6,10.
用较小两条线段的和与第三条线段做比较;
若较小两条线段的和大于第三条线段,就能保证任意两条线段的和大于第三条线段.
解决这类问题我们通常用哪两条线段的和与
第三条线段做比较?为什么?
解:设底边长为x
cm,则腰长为2x
cm.
x
+
2x
+
2x
=18.
解得
x
=3.6.
所以,三边长分别为3.6
cm,7.2
cm,7.2
cm.
例1 用一条长为18
cm的细绳围成一个等腰三角形.(1)如果腰长是底边的2倍,那么各边的长是多少?
例1 用一条长为18
cm的细绳围成一个等腰三角形.(2)能围成有一边的长是4
cm的等腰三角形吗?为什么?
解:①如果4
cm长的边为底边,设腰长为x
cm,则
4
+
2x
=
18.
解得
x
=
7.
②如果4
cm长的边为腰,设底边长为x
cm,则
4×2
+
x
=
18.
解得
x
=
10.
例2 用一条长为18
cm的细绳围成一个等腰三角形.(2)能围成有一边的长为4
cm的等腰三角形吗?为什么?
解:因为4
+
4<10,
不符合三角形两边的和大于第三边,
所以不能围成腰长为4
的等腰三角形.
由以上讨论可知,第①种情况可以围成底边
长为4
cm的等腰三角形.
练习
①一个等腰三角形的周长为24cm,只知其中一边的长为7cm,则这个等腰三角形的腰长为_________cm.
②下列长度的线段不能组成三角形的是(
)
A.
3,8,4
B.
4,9,6
C.
15,20,8
D.
9,15,8
7
或8.5
A
随堂演练
1.下列说法:①等边三角形是等腰三角形;②三角形按边分类可分为等腰三角形、等边三角形、不等边三角形;③三角形的两边之差大于第三边;④三角形按角分类应分为锐角三角形、直角三角形、钝角三角形.
其中正确的有(
)
A.1个
B.2个
C.3个
D.4个
B
基础巩固
2.已知三角形的一边长为5cm,另一边长为3cm.则第三边的长x
的取值范围是________________.
2cm
<
x
<
8cm
解:(1)设底边长为x厘米,则腰长为2x
厘米.
x
+
2x
+
2x
=
20
解得
x
=
4.
所以三边长分别为4cm,8cm,8cm.
3.等腰三角形的周长为20厘米.
(1)若已知腰长是底长的2倍,求各边的长;
(2)若已知一边长为6厘米,求其他两边的长.
拓展延伸
解:(2)如果6
厘米长的边为底边,设腰长为x
厘米,则6
+
2x
=
20,解得x
=
7;
如果6厘米长的边为腰,设底边长为x
厘米,则2×6
+
x
=
20,解得x
=
8.
由以上讨论可知,其他两边的长分别为7
厘米,7
厘米或6
厘米,8
厘米.
三角形
概念
分类
性质
三角形两边的和大于第三边.
三角形两边的差小于第三边.
A
B
C
a
b
c
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
教学过程中,强调学生自主探索和合作交流,经历观察、猜想、试验、数据处理、归纳、类比等思维过程,从中获得数学知识与技能,体验教学活动的方法,同时升华学生的情感、态度和价值观.
教学反思
11.1.1三角形的边
——三角形的有关概念、分类及三边关系
第十一章
三角形
三角形是我们早已熟悉的图形,你能列举出日常生活中形如三角形的物体吗?对于三角形,你了解了哪些方面的知识?你能画一个三角形吗?
新课导入
学习目标:
1.记住三角形的有关概念.
2.会用符号表示三角形,会对三角形进行分类.
3.能说出三角形的三边关系,并能运用三角形
三边关系解决相关问题.
学习重、难点:
重点:三角形及其有关的概念;三角形的分类.
难点:三角形三边关系及应用.
推进新课
理解三角形的有关概念
问题1
三角形是我们熟悉的图形,观察下列图片,你能说一说三角形是怎样的图形吗?
知识点1
边:AB,BC,AC
或
c,a,b.
顶点:点A,B,C
.
内角:∠A
,∠B
,∠C.
追问:对于教科书图11.1-1中的三角形,你能说出它的边、顶点与内角吗?
A
B
C
a
b
c
问题2
我们知道,三角形按角可以分为锐角三角形、直角三角形和钝角三角形.你能按照边的关系对三角形进行分类吗?
三边都不相等的三角形
三角形
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
理解三角形的分类
知识点2
按边分类后的特殊三角形之间有什么关系?它们的边和角怎样命名?
腰
腰
底边
三角形
顶角
底角
底角
图中有5个三角形.
用符号表示为:
△ABE,
△ABC,
△BEC,
△EDC,
△BDC.
练习1 图中有几个三角形?用符号表示这些三角形.
A
B
C
D
E
(4)
练习2 下列说法正确的有_______.
(1)锐角三角形是三条边都不相等的三角形;
(2)直角三角形不是等腰三角形;
(3)等腰三角形是等边三角形;
(4)等边三角形是等腰三角形.
△ABC,△AEC,△ADC
练习3 如图,共有6个三角形,其中以AC为边的三角形是_________________________;以∠B为内角的三角形有_________________________.
△ABC,△DBC,△EBC
AB
+
AC
>BC,
①
AC
+
BC
>AB,
②
AB
+
BC
>AC.
③
即三角形两边的和大于第三边.
问题3
如图,任意画一个△ABC,一只小虫从点B
出发,沿三角形的边爬到点C,它有几条路线可以选择?各条线路的长一样吗?你能运用所学知识解释你的发现吗?由此你能推出三条边之间有怎样的关系?
B
C
A
探索与证明三角形三边的关系
知识点3
三角形两边的差小于第三边.
由不等式②③移项可得
BC
>AB
-AC,
BC
>AC
-AB.由此你能得出什么结论?
B
C
A
解:(1)能.因为3
+
4>5,3
+
5>4,4
+
5>3,
符合三角形两边的和大于第三边.
(2)不能.因为5
+
6
=11,
不符合三角形两边的和大于第三边.
(3)能.因为5
+
6>10,10
+
6>5,10
+
5>6,
符合三角形两边的和大于第三边.
问题:下列长度的三条线段能否组成三角形?为什么?(1)3,4,5;(2)5,6,11;(3)5,6,10.
用较小两条线段的和与第三条线段做比较;
若较小两条线段的和大于第三条线段,就能保证任意两条线段的和大于第三条线段.
解决这类问题我们通常用哪两条线段的和与
第三条线段做比较?为什么?
解:设底边长为x
cm,则腰长为2x
cm.
x
+
2x
+
2x
=18.
解得
x
=3.6.
所以,三边长分别为3.6
cm,7.2
cm,7.2
cm.
例1 用一条长为18
cm的细绳围成一个等腰三角形.(1)如果腰长是底边的2倍,那么各边的长是多少?
例1 用一条长为18
cm的细绳围成一个等腰三角形.(2)能围成有一边的长是4
cm的等腰三角形吗?为什么?
解:①如果4
cm长的边为底边,设腰长为x
cm,则
4
+
2x
=
18.
解得
x
=
7.
②如果4
cm长的边为腰,设底边长为x
cm,则
4×2
+
x
=
18.
解得
x
=
10.
例2 用一条长为18
cm的细绳围成一个等腰三角形.(2)能围成有一边的长为4
cm的等腰三角形吗?为什么?
解:因为4
+
4<10,
不符合三角形两边的和大于第三边,
所以不能围成腰长为4
的等腰三角形.
由以上讨论可知,第①种情况可以围成底边
长为4
cm的等腰三角形.
练习
①一个等腰三角形的周长为24cm,只知其中一边的长为7cm,则这个等腰三角形的腰长为_________cm.
②下列长度的线段不能组成三角形的是(
)
A.
3,8,4
B.
4,9,6
C.
15,20,8
D.
9,15,8
7
或8.5
A
随堂演练
1.下列说法:①等边三角形是等腰三角形;②三角形按边分类可分为等腰三角形、等边三角形、不等边三角形;③三角形的两边之差大于第三边;④三角形按角分类应分为锐角三角形、直角三角形、钝角三角形.
其中正确的有(
)
A.1个
B.2个
C.3个
D.4个
B
基础巩固
2.已知三角形的一边长为5cm,另一边长为3cm.则第三边的长x
的取值范围是________________.
2cm
<
x
<
8cm
解:(1)设底边长为x厘米,则腰长为2x
厘米.
x
+
2x
+
2x
=
20
解得
x
=
4.
所以三边长分别为4cm,8cm,8cm.
3.等腰三角形的周长为20厘米.
(1)若已知腰长是底长的2倍,求各边的长;
(2)若已知一边长为6厘米,求其他两边的长.
拓展延伸
解:(2)如果6
厘米长的边为底边,设腰长为x
厘米,则6
+
2x
=
20,解得x
=
7;
如果6厘米长的边为腰,设底边长为x
厘米,则2×6
+
x
=
20,解得x
=
8.
由以上讨论可知,其他两边的长分别为7
厘米,7
厘米或6
厘米,8
厘米.
三角形
概念
分类
性质
三角形两边的和大于第三边.
三角形两边的差小于第三边.
A
B
C
a
b
c
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
教学过程中,强调学生自主探索和合作交流,经历观察、猜想、试验、数据处理、归纳、类比等思维过程,从中获得数学知识与技能,体验教学活动的方法,同时升华学生的情感、态度和价值观.
教学反思
