2019-2020学年上海市浦东新区第四教育署七年级(下)期末数学试卷(五四学制)(word解析版)
文档属性
| 名称 | 2019-2020学年上海市浦东新区第四教育署七年级(下)期末数学试卷(五四学制)(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 140.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-17 00:00:00 | ||
图片预览



文档简介
2019-2020学年上海市浦东新区第四教育署七年级(下)期末数学试卷(五四学制)
一、选择题(本大题共6题,每题2分,满分12分)(每题只有一个选项正确)
1.(2分)下列运算正确的是( )
A.2﹣3=﹣6
B.=﹣
C.=±2
D.2×3=5
2.(2分)下列各数:,0,,,0.3030030003,1﹣中,无理数个数为( )
A.2个
B.3个
C.4个
D.5个
3.(2分)下列说法中错误的是( )
A.有两个角及它们的夹边对应相等的两个三角形全等
B.有两个角及其中一个角的对边对应相等的两个三角形全等
C.有两条边及它们的夹角对应相等的两个三角形全等
D.有两条边及其中一条边的对角对应相等的两个三角形全等
4.(2分)在直角坐标平面内,点P(﹣2,3)向下平移2个单位得到点Q,则点Q的坐标是( )
A.(﹣2,1)
B.(﹣2,5)
C.(0,3)
D.(﹣4,3)
5.(2分)如图,BA∥DE,∠B=30°,∠D=40°,则∠C的度数是( )
A.10°
B.35°
C.70°
D.80°
6.(2分)如图所示,已知OA=OB,OC=OD,AD、BC相交于点E,则图中全等三角形共有( )
A.2对
B.3对
C.4对
D.5对
二、填空题(本大题共12题,每题3分,满分36分)
7.(3分)25的平方根等于
.
8.(3分)计算:=
.
9.(3分)计算:=
.
10.(3分)把化成幂的形式:
.
11.(3分)计算:(﹣)﹣2=
.
12.(3分)我国最长的河流长江全长约为6300000米,将6300000用科学记数法表示应为
.(保留3个有效数字)
13.(3分)一个等腰三角形的两边长分别是2cm、5cm,则它的周长为
cm.
14.(3分)△ABC的三个内角的度数之比是1:2:3,若按角分类,则△ABC是
三角形.
15.(3分)如图,直线a、b被直线c所截(即直线c与直线a、b都相交),且a∥b,若∠1=118°,则∠2的度数=
度.
16.(3分)如图,直线AB和CD交于O点,EO⊥CD,∠EOB=50°,则∠AOC=
.
17.(3分)如图,在△ABC中,AB=6,AC=9,BO、CO分别是∠ABC、∠ACB的平分线,MN经过点O,且MN∥BC,MN分别交AB、AC于点M、N,则△AMN的周长是
.
18.(3分)如图,在△ABC中,∠CAB=65°,把△ABC绕着点A逆时针旋转到△AB'C',联结CC',并且使CC'∥AB,那么旋转角的度数为
度.
三、简答题(本大题共4题,第19、20题每题5分,第21、22题每题6分,满分22分)
19.(5分)计算:8﹣()2×÷+()﹣1.
20.(5分)利用幂的运算性质计算:(3×9).
21.(6分)如图,已知∠COF+∠C=180°,∠C=∠B.说明AB∥EF的理由.
22.(6分)阅读并填空:
如图:根据六年级第二学期学过的用直尺、圆规作线段中点的方法,画出了线段AB的中点C,请说明这种方法正确的理由.
解:连接AE、BE、AF、BF.
在△AEF和△BEF中,
EF=EF(
),
=
(画弧时所取的半径相等),
=
(画弧时所取的半径相等).
所以△AEF≌△BEF
(
).
所以∠AEF=∠BEF
(
).
又AE=BE,
所以AC=BC
(
).
即点C是线段AB的中点.
四、解答题(本大题共4题,第23、24题每题7分,第25、26题每题8分,满分30分)
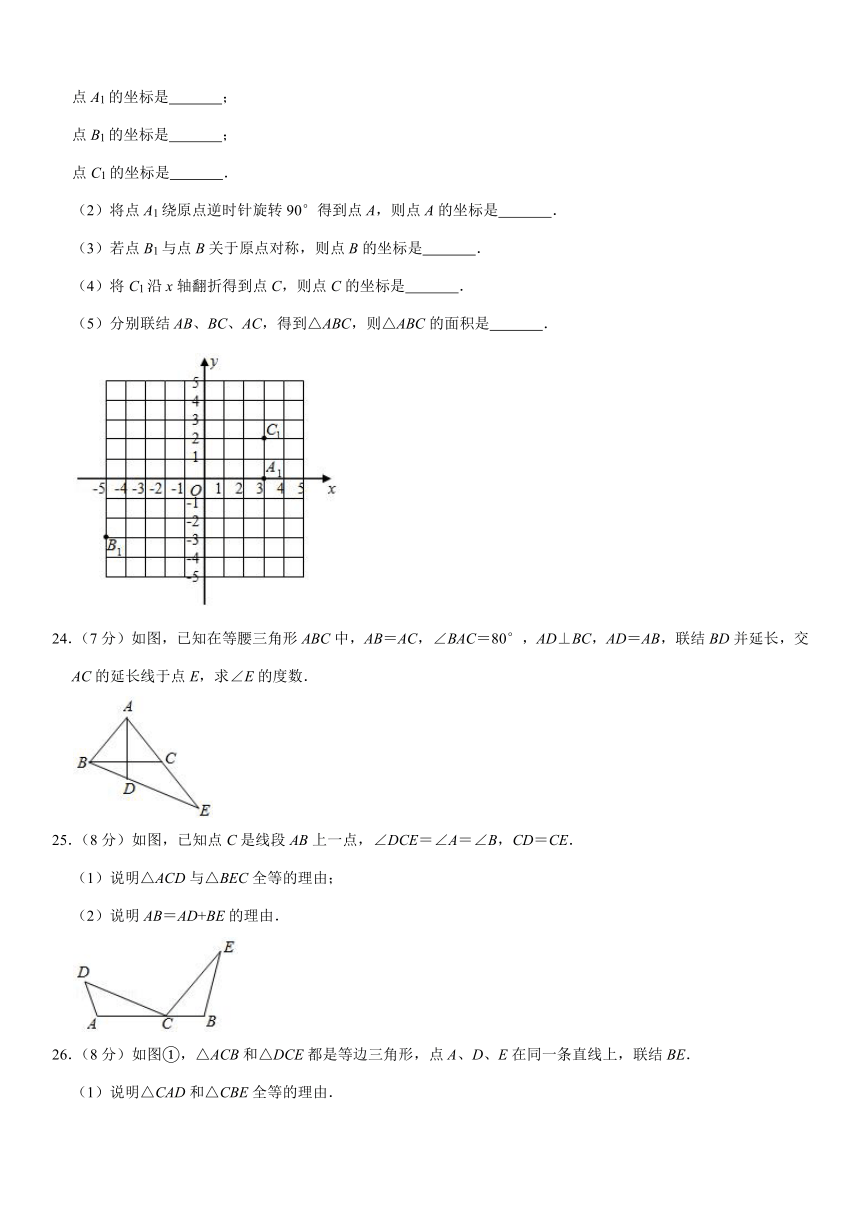
23.(7分)在直角坐标平面内,点A1、B1、C1的坐标如图所示.
(1)请写出点A1、B1、C1的坐标:
点A1的坐标是
;
点B1的坐标是
;
点C1的坐标是
.
(2)将点A1绕原点逆时针旋转90°得到点A,则点A的坐标是
.
(3)若点B1与点B关于原点对称,则点B的坐标是
.
(4)将C1沿x轴翻折得到点C,则点C的坐标是
.
(5)分别联结AB、BC、AC,得到△ABC,则△ABC的面积是
.
24.(7分)如图,已知在等腰三角形ABC中,AB=AC,∠BAC=80°,AD⊥BC,AD=AB,联结BD并延长,交AC的延长线于点E,求∠E的度数.
25.(8分)如图,已知点C是线段AB上一点,∠DCE=∠A=∠B,CD=CE.
(1)说明△ACD与△BEC全等的理由;
(2)说明AB=AD+BE的理由.
26.(8分)如图①,△ACB和△DCE都是等边三角形,点A、D、E在同一条直线上,联结BE.
(1)说明△CAD和△CBE全等的理由.
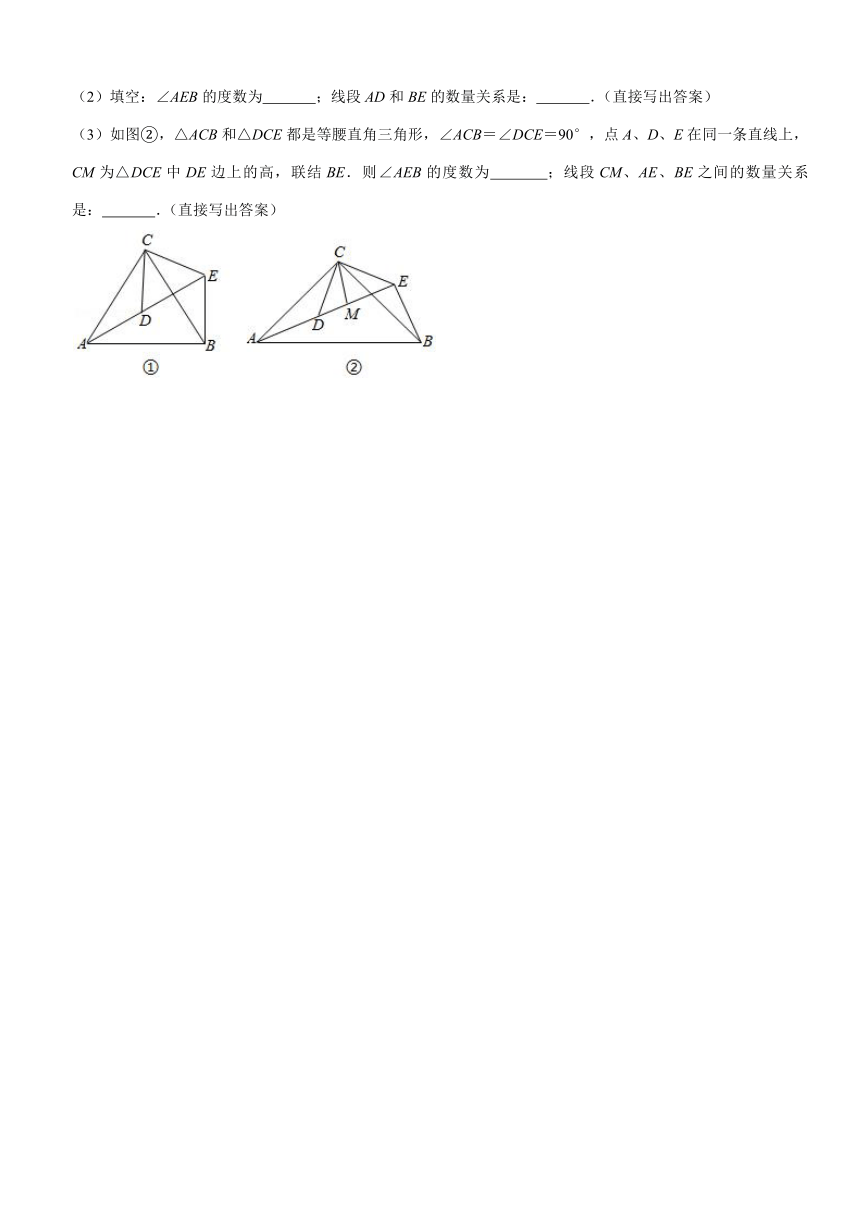
(2)填空:∠AEB的度数为
;线段AD和BE的数量关系是:
.(直接写出答案)
(3)如图②,△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一条直线上,CM为△DCE中DE边上的高,联结BE.则∠AEB的度数为
;线段CM、AE、BE之间的数量关系是:
.(直接写出答案)
2019-2020学年上海市浦东新区第四教育署七年级(下)期末数学试卷(五四学制)
参考答案与试题解析
一、选择题(本大题共6题,每题2分,满分12分)(每题只有一个选项正确)
1.【解答】解:A.2﹣3==,此选项计算错误;
B.=﹣,此选项计算正确;
C.=2,此选项计算错误;
D.2×3=6,此选项计算错误;
故选:B.
2.【解答】解:在所列实数中,无理数有、1﹣这2个,
故选:A.
3.【解答】解:A、有两个角及它们的夹边对应相等的两个三角形全等,是“ASA”,说法正确;
B、两个角及其中一个角的对边对应相等的两个三角形全等,是“AAS”,说法正确;
C、有两条边及它们的夹角对应相等的两个三角形全等,是“SAS”,说法正确;
D、有两条边及其中一条边的对角对应相等的两个三角形不一定全等,说法错误;
故选:D.
4.【解答】解:点P的坐标为(﹣2,3),将点P向下平移2个单位后,
所得点的横坐标是﹣2,纵坐标为3﹣2=1,即(﹣2,1).
故选:A.
5.【解答】解:过点C作FC∥AB,
∵BA∥DE,
∴BA∥DE∥FC,
∴∠B=∠BCF,∠D=∠DCF,
∵∠B=30°,∠D=40°,
∴∠BCF=30°,∠DCF=40°,
∴∠BCD=70°,
故选:C.
6.【解答】解:在△AOD和△BOC中,
∴△AOD≌△BOC(SAS);
∴∠A=∠B,
∵OA=OB,OC=OD,
∴AC=BD,
在△CAE和△ODBE中,
∴△CAE≌△DBE(AAS);
∴AE=BE,
在△AOE和△BOE中,
∴△AOE≌△BOE(SSS);
在△OCE和△ODE中,
∴△OCE≌△ODE(SSS).
故选:C.
二、填空题(本大题共12题,每题3分,满分36分)
7.【解答】解:25的平方根等于±5,
故答案为:±5
8.【解答】解:==6.
故答案为:6
9.【解答】解:因为>,
所以﹣>0,
所以=|﹣|=﹣.
故答案为:﹣.
10.【解答】解:==,
把化成幂的形式为:.
故答案为:.
11.【解答】解:(﹣)﹣2===.
故答案为:.
12.【解答】解:将6300000用科学记数法表示为:6.3×106.
故答案为:6.3×106.
13.【解答】解:分两种情况讨论
①腰长为5时,三边为5、5、2,满足三角形的性质,周长=5+5+2=12cm;
②腰长为2cm时,三边为5、2、2,
∵2+2=4<5,
∴不满足构成三角形.
∴周长为12cm.
故答案为:12.
14.【解答】解:设一份为k°,则三个内角的度数分别为k°,2k°,3k°.
则k°+2k°+3k°=180°,
解得k°=30°
∴2k°=60°,3k°=90°,
所以这个三角形是直角三角形.
故答案为:直角.
15.【解答】解:∵a∥b,
∴∠1=∠3=118°,
∵∠3与∠2互为邻补角,
∴∠2=62°.
16.【解答】解:∵EO⊥CD,
∴∠COE=90°,
∴∠AOC=180°﹣∠BOE﹣∠COE=180°﹣50°﹣90°=40°
故答案为:40°.
17.【解答】解:∵在△ABC中,∠BAC与∠ACB的平分线相交于点O,
∴∠ABO=∠OBC,∠ACO=∠BCO,
∵MN∥BC,
∴∠MOB=∠OBC,∠NOC=∠OCB,
∴∠ABO=∠MOB,∠ACO=∠NOC,
∴BM=OM,CN=ON,
∴△AMN的周长是:AM+NM+AN=AM+OM+ON+AN=AM+BM+CN+AN=AB+AC=9+6=15.
故答案为:15.
18.【解答】解:如图,
∵△ABC绕着点A逆时针旋转到△AB'C',
∴旋转角等于∠CAC′,AC=AC′,
∴∠ACC′=∠AC′C,
∵CC'∥AB,
∴∠ACC′=∠CAB=65°,
∴∠CAC′=180°﹣65°﹣65°=50°.
故答案为50.
三、简答题(本大题共4题,第19、20题每题5分,第21、22题每题6分,满分22分)
19.【解答】解:原式=﹣3×÷+﹣1
=﹣3+﹣1
=4﹣2﹣1
=3﹣2.
20.【解答】解:原式=×
=×
=
=3.
21.【解答】解:∵∠COF+∠C=180°,
∴EF∥CD,
∵∠C=∠B,
∴AB∥CD,
∴AB∥EF.
22.【解答】解:在△AEF和△BEF中,
,
∴△AEF≌△BEF(SSS),
∴∠AEF=∠BEF(全等三角形的对应角相等),
∵AE=BE,
∴AC=BC(等腰三角形的三线合一),
∴C是线段AB的中点.
故答案为:公共边,AE、BE,AF、BF,S.S.S,全等三角形对应角相等,等腰三角形三线合一.
四、解答题(本大题共4题,第23、24题每题7分,第25、26题每题8分,满分30分)
23.【解答】解:(1)在直角坐标平面内,点A1、B1、C1的坐标如图所示:
点A1的坐标是(3,0);点B1的坐标是
(﹣5,﹣3);点C1的坐标是
(3,2),
故答案为(3,0);(﹣5,﹣3);(3,2).
(2)将点A1绕原点逆时针旋转90°得到点A,则点A的坐标是(0,3),
故答案为(0,3);
(3)若点B1与点B关于原点对称,则点B的坐标是(5,3),
故答案为(5,3);
(4)将C1沿x轴翻折得到点C,则点C的坐标是(3,﹣2),
故答案为(3,﹣2);
(5)分别联结AB、BC、AC,得到△ABC,则△ABC的面积是:5×5﹣﹣=,
故答案为.
24.【解答】解:∵AB=AC,∠BAC=80°,AD⊥BC,
∴∠BAD=∠CAD=∠BAC=40°,
∵AD=AB,
∴∠BDA=×(180°﹣40°)=70°,
∴∠E=∠BDA﹣∠CAD=70°﹣40°=30°.
25.【解答】解:(1)∵∠DCE=∠A,
∴∠D+∠ACD=∠ACD+∠BCE,
∴∠D=∠BCE,
在△ACD和△BEC中,
,
∴△ACD≌△BEC(AAS);
(2)∵△ACD≌△BEC,
∴AD=BC,AC=BE,
∴AC+BC=AD+BE,
即AB=AD+BE.
26.【解答】解:(1)如图①,∵△ACB和△DCE均为等边三角形,
∴AC=BC,DC=CE,∠ACB=∠DCE=60°,
∵点A、D、E在同一条直线上,
∴∠ADC=120°,
∵∠ACB﹣∠DCB=∠DCE﹣∠DCB,
∴∠ACD=∠BCE,且AC=BC,DC=CE,
∴△CAD≌△CBE(SAS)
(2)如图①∵△DCE为等边三角形,
∴∠CDE=∠CED=60°,
∵点A、D、E在同一条直线上,
∴∠ADC=120°,
∵△CAD≌△CBE,
∴AD=BE,∠BEC=∠ADC=120°,
∴∠AEB=120°﹣60°=60°,
故答案为:60°,AD=BE;
(3)结论:∠AEB=90°,AE=BE+2CM,
理由:如图②,
∵△ACB和△DCE均为等腰直角三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠ADC=∠BEC,
∵△DCE为等腰直角三角形,
∴∠CDE=∠CED=45°,
∵点A,D,E在同一直线上,
∴∠ADC=135°,
∴∠BEC=135°,
∴∠AEB=∠BEC﹣∠CED=135°﹣45°=90°,
∵CD=CE,CM⊥DE,
∴DM=ME,
∵∠DCE=90°,
∴DM=ME=CM,
∴AE=AD+DE=BE+2CM.
故答案为:90°,AE=BE+2CM.
一、选择题(本大题共6题,每题2分,满分12分)(每题只有一个选项正确)
1.(2分)下列运算正确的是( )
A.2﹣3=﹣6
B.=﹣
C.=±2
D.2×3=5
2.(2分)下列各数:,0,,,0.3030030003,1﹣中,无理数个数为( )
A.2个
B.3个
C.4个
D.5个
3.(2分)下列说法中错误的是( )
A.有两个角及它们的夹边对应相等的两个三角形全等
B.有两个角及其中一个角的对边对应相等的两个三角形全等
C.有两条边及它们的夹角对应相等的两个三角形全等
D.有两条边及其中一条边的对角对应相等的两个三角形全等
4.(2分)在直角坐标平面内,点P(﹣2,3)向下平移2个单位得到点Q,则点Q的坐标是( )
A.(﹣2,1)
B.(﹣2,5)
C.(0,3)
D.(﹣4,3)
5.(2分)如图,BA∥DE,∠B=30°,∠D=40°,则∠C的度数是( )
A.10°
B.35°
C.70°
D.80°
6.(2分)如图所示,已知OA=OB,OC=OD,AD、BC相交于点E,则图中全等三角形共有( )
A.2对
B.3对
C.4对
D.5对
二、填空题(本大题共12题,每题3分,满分36分)
7.(3分)25的平方根等于
.
8.(3分)计算:=
.
9.(3分)计算:=
.
10.(3分)把化成幂的形式:
.
11.(3分)计算:(﹣)﹣2=
.
12.(3分)我国最长的河流长江全长约为6300000米,将6300000用科学记数法表示应为
.(保留3个有效数字)
13.(3分)一个等腰三角形的两边长分别是2cm、5cm,则它的周长为
cm.
14.(3分)△ABC的三个内角的度数之比是1:2:3,若按角分类,则△ABC是
三角形.
15.(3分)如图,直线a、b被直线c所截(即直线c与直线a、b都相交),且a∥b,若∠1=118°,则∠2的度数=
度.
16.(3分)如图,直线AB和CD交于O点,EO⊥CD,∠EOB=50°,则∠AOC=
.
17.(3分)如图,在△ABC中,AB=6,AC=9,BO、CO分别是∠ABC、∠ACB的平分线,MN经过点O,且MN∥BC,MN分别交AB、AC于点M、N,则△AMN的周长是
.
18.(3分)如图,在△ABC中,∠CAB=65°,把△ABC绕着点A逆时针旋转到△AB'C',联结CC',并且使CC'∥AB,那么旋转角的度数为
度.
三、简答题(本大题共4题,第19、20题每题5分,第21、22题每题6分,满分22分)
19.(5分)计算:8﹣()2×÷+()﹣1.
20.(5分)利用幂的运算性质计算:(3×9).
21.(6分)如图,已知∠COF+∠C=180°,∠C=∠B.说明AB∥EF的理由.
22.(6分)阅读并填空:
如图:根据六年级第二学期学过的用直尺、圆规作线段中点的方法,画出了线段AB的中点C,请说明这种方法正确的理由.
解:连接AE、BE、AF、BF.
在△AEF和△BEF中,
EF=EF(
),
=
(画弧时所取的半径相等),
=
(画弧时所取的半径相等).
所以△AEF≌△BEF
(
).
所以∠AEF=∠BEF
(
).
又AE=BE,
所以AC=BC
(
).
即点C是线段AB的中点.
四、解答题(本大题共4题,第23、24题每题7分,第25、26题每题8分,满分30分)
23.(7分)在直角坐标平面内,点A1、B1、C1的坐标如图所示.
(1)请写出点A1、B1、C1的坐标:
点A1的坐标是
;
点B1的坐标是
;
点C1的坐标是
.
(2)将点A1绕原点逆时针旋转90°得到点A,则点A的坐标是
.
(3)若点B1与点B关于原点对称,则点B的坐标是
.
(4)将C1沿x轴翻折得到点C,则点C的坐标是
.
(5)分别联结AB、BC、AC,得到△ABC,则△ABC的面积是
.
24.(7分)如图,已知在等腰三角形ABC中,AB=AC,∠BAC=80°,AD⊥BC,AD=AB,联结BD并延长,交AC的延长线于点E,求∠E的度数.
25.(8分)如图,已知点C是线段AB上一点,∠DCE=∠A=∠B,CD=CE.
(1)说明△ACD与△BEC全等的理由;
(2)说明AB=AD+BE的理由.
26.(8分)如图①,△ACB和△DCE都是等边三角形,点A、D、E在同一条直线上,联结BE.
(1)说明△CAD和△CBE全等的理由.
(2)填空:∠AEB的度数为
;线段AD和BE的数量关系是:
.(直接写出答案)
(3)如图②,△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一条直线上,CM为△DCE中DE边上的高,联结BE.则∠AEB的度数为
;线段CM、AE、BE之间的数量关系是:
.(直接写出答案)
2019-2020学年上海市浦东新区第四教育署七年级(下)期末数学试卷(五四学制)
参考答案与试题解析
一、选择题(本大题共6题,每题2分,满分12分)(每题只有一个选项正确)
1.【解答】解:A.2﹣3==,此选项计算错误;
B.=﹣,此选项计算正确;
C.=2,此选项计算错误;
D.2×3=6,此选项计算错误;
故选:B.
2.【解答】解:在所列实数中,无理数有、1﹣这2个,
故选:A.
3.【解答】解:A、有两个角及它们的夹边对应相等的两个三角形全等,是“ASA”,说法正确;
B、两个角及其中一个角的对边对应相等的两个三角形全等,是“AAS”,说法正确;
C、有两条边及它们的夹角对应相等的两个三角形全等,是“SAS”,说法正确;
D、有两条边及其中一条边的对角对应相等的两个三角形不一定全等,说法错误;
故选:D.
4.【解答】解:点P的坐标为(﹣2,3),将点P向下平移2个单位后,
所得点的横坐标是﹣2,纵坐标为3﹣2=1,即(﹣2,1).
故选:A.
5.【解答】解:过点C作FC∥AB,
∵BA∥DE,
∴BA∥DE∥FC,
∴∠B=∠BCF,∠D=∠DCF,
∵∠B=30°,∠D=40°,
∴∠BCF=30°,∠DCF=40°,
∴∠BCD=70°,
故选:C.
6.【解答】解:在△AOD和△BOC中,
∴△AOD≌△BOC(SAS);
∴∠A=∠B,
∵OA=OB,OC=OD,
∴AC=BD,
在△CAE和△ODBE中,
∴△CAE≌△DBE(AAS);
∴AE=BE,
在△AOE和△BOE中,
∴△AOE≌△BOE(SSS);
在△OCE和△ODE中,
∴△OCE≌△ODE(SSS).
故选:C.
二、填空题(本大题共12题,每题3分,满分36分)
7.【解答】解:25的平方根等于±5,
故答案为:±5
8.【解答】解:==6.
故答案为:6
9.【解答】解:因为>,
所以﹣>0,
所以=|﹣|=﹣.
故答案为:﹣.
10.【解答】解:==,
把化成幂的形式为:.
故答案为:.
11.【解答】解:(﹣)﹣2===.
故答案为:.
12.【解答】解:将6300000用科学记数法表示为:6.3×106.
故答案为:6.3×106.
13.【解答】解:分两种情况讨论
①腰长为5时,三边为5、5、2,满足三角形的性质,周长=5+5+2=12cm;
②腰长为2cm时,三边为5、2、2,
∵2+2=4<5,
∴不满足构成三角形.
∴周长为12cm.
故答案为:12.
14.【解答】解:设一份为k°,则三个内角的度数分别为k°,2k°,3k°.
则k°+2k°+3k°=180°,
解得k°=30°
∴2k°=60°,3k°=90°,
所以这个三角形是直角三角形.
故答案为:直角.
15.【解答】解:∵a∥b,
∴∠1=∠3=118°,
∵∠3与∠2互为邻补角,
∴∠2=62°.
16.【解答】解:∵EO⊥CD,
∴∠COE=90°,
∴∠AOC=180°﹣∠BOE﹣∠COE=180°﹣50°﹣90°=40°
故答案为:40°.
17.【解答】解:∵在△ABC中,∠BAC与∠ACB的平分线相交于点O,
∴∠ABO=∠OBC,∠ACO=∠BCO,
∵MN∥BC,
∴∠MOB=∠OBC,∠NOC=∠OCB,
∴∠ABO=∠MOB,∠ACO=∠NOC,
∴BM=OM,CN=ON,
∴△AMN的周长是:AM+NM+AN=AM+OM+ON+AN=AM+BM+CN+AN=AB+AC=9+6=15.
故答案为:15.
18.【解答】解:如图,
∵△ABC绕着点A逆时针旋转到△AB'C',
∴旋转角等于∠CAC′,AC=AC′,
∴∠ACC′=∠AC′C,
∵CC'∥AB,
∴∠ACC′=∠CAB=65°,
∴∠CAC′=180°﹣65°﹣65°=50°.
故答案为50.
三、简答题(本大题共4题,第19、20题每题5分,第21、22题每题6分,满分22分)
19.【解答】解:原式=﹣3×÷+﹣1
=﹣3+﹣1
=4﹣2﹣1
=3﹣2.
20.【解答】解:原式=×
=×
=
=3.
21.【解答】解:∵∠COF+∠C=180°,
∴EF∥CD,
∵∠C=∠B,
∴AB∥CD,
∴AB∥EF.
22.【解答】解:在△AEF和△BEF中,
,
∴△AEF≌△BEF(SSS),
∴∠AEF=∠BEF(全等三角形的对应角相等),
∵AE=BE,
∴AC=BC(等腰三角形的三线合一),
∴C是线段AB的中点.
故答案为:公共边,AE、BE,AF、BF,S.S.S,全等三角形对应角相等,等腰三角形三线合一.
四、解答题(本大题共4题,第23、24题每题7分,第25、26题每题8分,满分30分)
23.【解答】解:(1)在直角坐标平面内,点A1、B1、C1的坐标如图所示:
点A1的坐标是(3,0);点B1的坐标是
(﹣5,﹣3);点C1的坐标是
(3,2),
故答案为(3,0);(﹣5,﹣3);(3,2).
(2)将点A1绕原点逆时针旋转90°得到点A,则点A的坐标是(0,3),
故答案为(0,3);
(3)若点B1与点B关于原点对称,则点B的坐标是(5,3),
故答案为(5,3);
(4)将C1沿x轴翻折得到点C,则点C的坐标是(3,﹣2),
故答案为(3,﹣2);
(5)分别联结AB、BC、AC,得到△ABC,则△ABC的面积是:5×5﹣﹣=,
故答案为.
24.【解答】解:∵AB=AC,∠BAC=80°,AD⊥BC,
∴∠BAD=∠CAD=∠BAC=40°,
∵AD=AB,
∴∠BDA=×(180°﹣40°)=70°,
∴∠E=∠BDA﹣∠CAD=70°﹣40°=30°.
25.【解答】解:(1)∵∠DCE=∠A,
∴∠D+∠ACD=∠ACD+∠BCE,
∴∠D=∠BCE,
在△ACD和△BEC中,
,
∴△ACD≌△BEC(AAS);
(2)∵△ACD≌△BEC,
∴AD=BC,AC=BE,
∴AC+BC=AD+BE,
即AB=AD+BE.
26.【解答】解:(1)如图①,∵△ACB和△DCE均为等边三角形,
∴AC=BC,DC=CE,∠ACB=∠DCE=60°,
∵点A、D、E在同一条直线上,
∴∠ADC=120°,
∵∠ACB﹣∠DCB=∠DCE﹣∠DCB,
∴∠ACD=∠BCE,且AC=BC,DC=CE,
∴△CAD≌△CBE(SAS)
(2)如图①∵△DCE为等边三角形,
∴∠CDE=∠CED=60°,
∵点A、D、E在同一条直线上,
∴∠ADC=120°,
∵△CAD≌△CBE,
∴AD=BE,∠BEC=∠ADC=120°,
∴∠AEB=120°﹣60°=60°,
故答案为:60°,AD=BE;
(3)结论:∠AEB=90°,AE=BE+2CM,
理由:如图②,
∵△ACB和△DCE均为等腰直角三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠ADC=∠BEC,
∵△DCE为等腰直角三角形,
∴∠CDE=∠CED=45°,
∵点A,D,E在同一直线上,
∴∠ADC=135°,
∴∠BEC=135°,
∴∠AEB=∠BEC﹣∠CED=135°﹣45°=90°,
∵CD=CE,CM⊥DE,
∴DM=ME,
∵∠DCE=90°,
∴DM=ME=CM,
∴AE=AD+DE=BE+2CM.
故答案为:90°,AE=BE+2CM.
同课章节目录
