江苏省徐州市2019-2020学年高一下学期期末抽测数学试题 Word版含答案
文档属性
| 名称 | 江苏省徐州市2019-2020学年高一下学期期末抽测数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-17 09:11:47 | ||
图片预览


文档简介
10185400114046002019——2020学年度第二学期期末抽测
高一年级数学试题
一、单项选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知点M(1,6) , N(7,3),则直线MN的斜率为
false2
2.false的值为
false
3. 圆false的圆心坐标为
false
4.下列命题错误的是
A.不在同一直线上的三点确定一个平面
B.两两相交且不共点的三条直线确定一个平面
C.如果两个平面垂直,那么其中一个平面内的直线一定垂直于另一个平面
D.如果两个平面平行,那么其中一个平面内的直线一定平行于另一个平面
5.下列叙述正确的是
A.频率是稳定的,概率是随机的
B.互斥事件一定不是对立事件,但是对立事件一定是互斥事件
C. 5张奖券中有1张有奖,甲先抽,乙后抽,那么乙比甲抽到有奖奖券的可能性小
D.若事件A发生的概率为P(A),则false
6. 在△ABC中,已知∠B=60°,边AB=4,且△ABC的面积为2,则边AC的长为
false
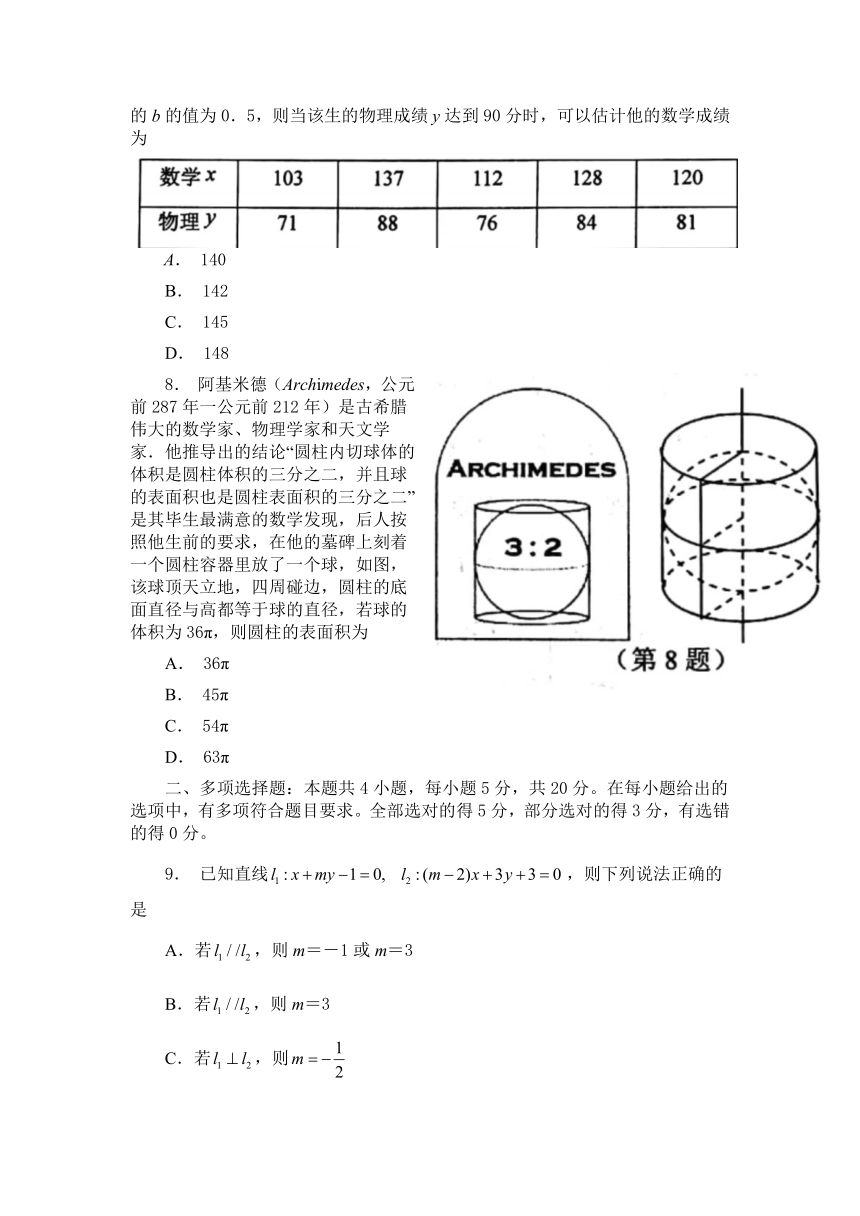
7. 某同学5次考试的数学成绩x与物理成绩y的统计数据如下表,已知该同学的物理成绩)与数学成绩x是线性相关的,根据数据可得回归方程false的b的值为0.5,则当该生的物理成绩y达到90分时,可以估计他的数学成绩为
А. 140
B. 142
C. 145
2620010194310D. 148
8. 阿基米德(Archimedes,公元前287年一公元前212年)是古希腊伟大的数学家、物理学家和天文学家.他推导出的结论“圆柱内切球体的体积是圆柱体积的三分之二,并且球的表面积也是圆柱表面积的三分之二”是其毕生最满意的数学发现,后人按照他生前的要求,在他的墓碑上刻着一个圆柱容器里放了一个球,如图,该球顶天立地,四周碰边,圆柱的底面直径与高都等于球的直径,若球的体积为36π,则圆柱的表面积为
A. 36π
B. 45π
C. 54π
D. 63π
二、多项选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得3分,有选错的得0分。
9. 已知直线false,则下列说法正确的是
A.若false,则m=-1或m=3
B.若false,则m=3
C.若false,则false
D.若false,则false
10.已知△ABC的内角A, B, C所对的边分别为a, b, c,则下列说法正确的是
A.若sinB>sinC,则B>C
B.若a=4, b=2, A=,则三角形有两解
C.若bcosB-ccosC=0,则△ABC一定为等腰直角三角形
D.若bcosC-ccosB—0,则△ABC一定为等腰三角形
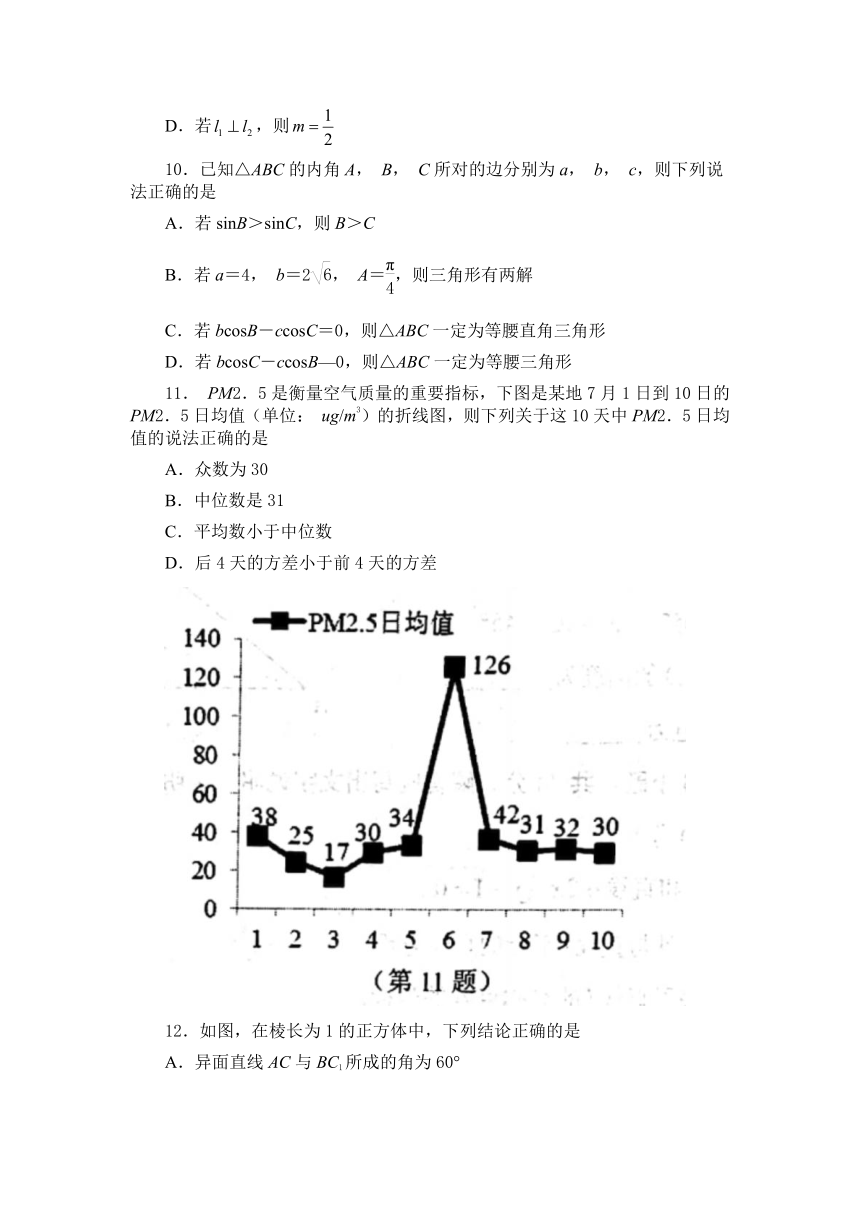
11. PM2.5是衡量空气质量的重要指标,下图是某地7月1日到10日的PM2.5日均值(单位: ug/m3)的折线图,则下列关于这10天中PM2.5日均值的说法正确的是
A.众数为30
B.中位数是31
C.平均数小于中位数
D.后4天的方差小于前4天的方差
12.如图,在棱长为1的正方体中,下列结论正确的是
A.异面直线AC与BC1所成的角为60°
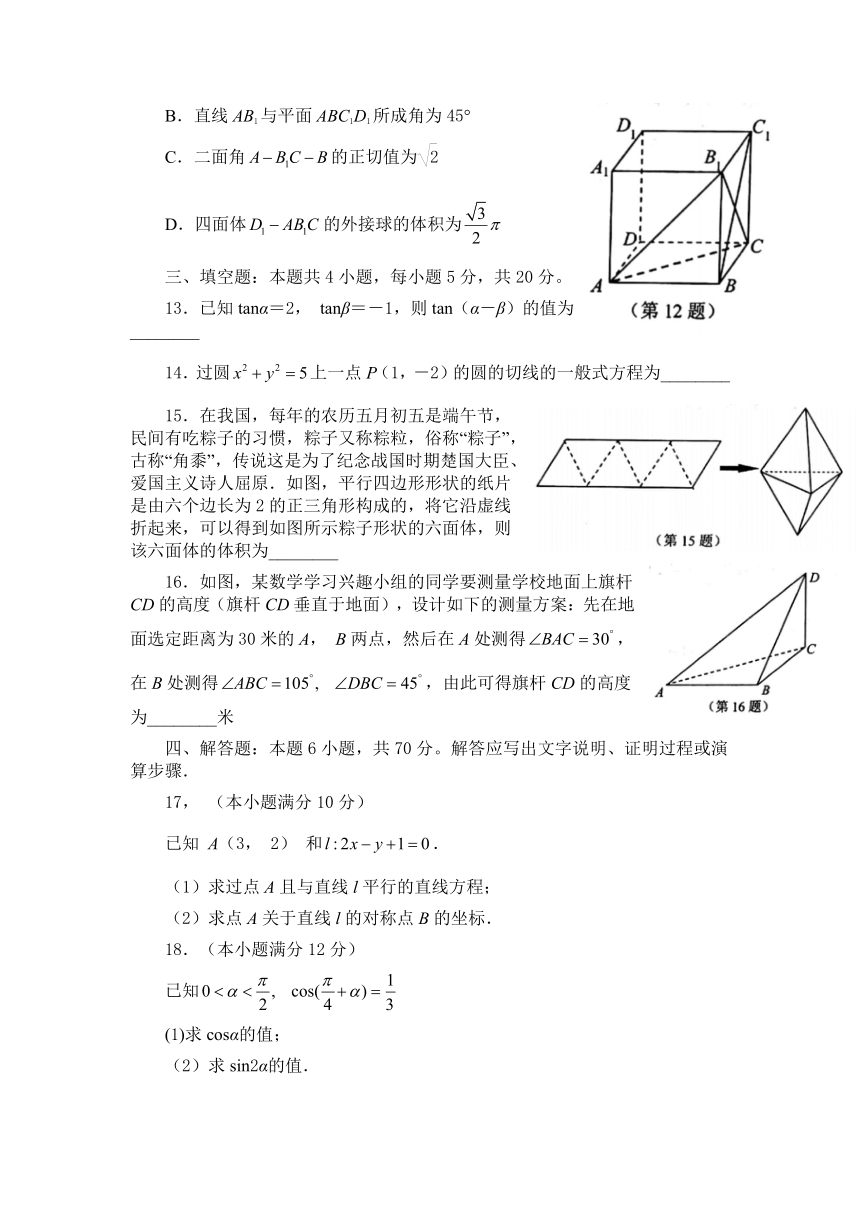
51625500B.直线AB1与平面ABC1D1所成角为45°
C.二面角false的正切值为
D.四面体false的外接球的体积为false
三、填空题:本题共4小题,每小题5分,共20分。
13.已知tanα=2, tanβ=-1,则tan(α-β)的值为________
14.过圆false上一点P(1,-2)的圆的切线的一般式方程为________
45529501313815right444515.在我国,每年的农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽粒,俗称“粽子”,古称“角黍”,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图,平行四边形形状的纸片是由六个边长为2的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为________
16.如图,某数学学习兴趣小组的同学要测量学校地面上旗杆CD的高度(旗杆CD垂直于地面),设计如下的测量方案:先在地面选定距离为30米的A, B两点,然后在A处测得false,在B处测得false,由此可得旗杆CD的高度为________米
四、解答题:本题6小题,共70分。解答应写出文字说明、证明过程或演算步骤.
17, (本小题满分10分)
已知 A(3, 2) 和false.
(1)求过点A且与直线l平行的直线方程;
(2)求点A关于直线l的对称点B的坐标.
18.(本小题满分12分)
已知false
(1)求cosα的值;
(2)求sin2α的值.
19. (本小题满分12分)
已知△ABC的内角A, B, C所对的边分别为a, b, c, A=,________且b=,请从false这三个条件中任选一个补充在横线上,求出此时△ABC的面积.
20. (本小题满分12分)
手机支付也称为移动支付(Mobile Payment),是当今社会比较流行的一种付款方式.某金融机构为了了解移动支付在大众中的熟知度,对15—65岁的人群作了问题为“你会使用移动支付吗?”的随机抽样调查,把回答“会”的100个人按照年龄分成5组,绘制成如图所示的频率分布表和频率分布直方图.
41592501601470 (1)求x,a的值;
(2)若从第1, 3组中用分层抽样的方法抽取5人,
求两组中分别抽取的人数;
(3)在(2)抽取的5人中再随机抽取2人,
求所抽取的2人来自同一个组的概率
21. (本小题满分12分)
如图,在P—ABC中, PA⊥面ABC, PA=2, CA=CB=AB=2, D为棱AB的中点,点E在棱PA上.
(1)若AE=EP,求证: PB∥平面CDE;
(2)求证:平面PAB⊥平面CDE;
39878000(3)若二面角B—CD—E的大小为120°,
求异面直线PC与DE所成角的余弦值.
22. (本小题满分12分)
如图,在平面直角坐标系xOy中,已知圆M: false,过点O及点A(-2,0)的圆N与圆M外切.
(1)求圆N的标准方程;
(2)若过点A的直线l被两圆截得的弦长相等,求直线l的方程;
(3)直线MN上是否存在点B,使得过点B分别作圆M与圆N的切线,切点分别为P, Q (不重合),满足BQ=2BP?若存在,求出点B的坐标,若不存在,请说明理由.
2019~2020学年度第二学期期末抽测
高一年级数学试题参考答案及评分标准
一、单项选择题:本题共8小题,每小题5分,共40分。
1.B 2.D 3.B 4.C 5.D 6.C 7.A 8.C
二、多项选择题:本题共4小题,每小题5分,共20分。
9.BD10.ABD11.AD 12.ACD
三、填空题:本题共4小题,每小题5分,共20分。
13.false14.false15.false16.false;false
四、解答题:本题6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17. (1)设所求直线的方程为false,将点false代入,得false,
故所求直线的方程为false.……………………………………………4分
(2)设false,则由false及线段false的中点在直线false上可得,
false…………………………………………………………8分
解得false,false,
所以点false的坐标为false.……………………………………………………10分
18.(1)因为false,所以false,所以false,
由false,所以false,
所以false
false.………………………………………6分
(2)false
false
false.………………………………………12分
19.情形一:若选择①false,
由余弦定理false,……………………………………2分
因为false,所以false; …………………………………………………………4分
情形二:若选择②false,则false,
因为false,所以false,……………………………………………………2分
因为false,所以false;………………………………………………………4分
情形三:若选择③false,则false,
所以false,………………………………………………………………2分
因为false,所以false,所以false,所以false;………4分
由正弦定理false,得false,……………………6分
因为false,false,所以false,………………………………8分
所以false,……10分
所以false.…………………12分
20.(1)由题意可知,false,…………………………………………2分
所以false,
从而false.…………………………………………………………4分
(2)第1,3组共有50人,所以抽取的比例是false,
则从第1组抽取的人数为false,……………………………………………6分
从第3组抽取的人数为false.……………………………………………8分
(3)设第1组抽取的2人为false,false,第3组抽取的3人为false,false,false,
则从这5人中随机抽取2人有如下种情形:
false,false,false,false,false,false,false,false,false,
false共有10个基本事件.………………………………………………………10分
其中符合“抽取的2人来自同一个组”的基本事件有false,false,false,
false共4个基本事件,
所以抽取的2人来自同一个组的概率false.………………………………12分
21.(1)由false知,false为棱false的中点,又因为false为棱false的中点,
所以在false中,false,因为false平面false,false平面false,
所以false平面false.………………………………………………………………2分
(2)因为false底面false,false平面false,所以false,
在false中,false,false为false的中点,所以false,
又因为false,false平面false,false平面false,
所以false平面false.………………………………………………………5分
又因为false平面false,所以平面false平面false.…………………………6分
(3)由题意知,二面角false的大小为false,
由(2)的证明可知,false平面false,又因为false平面false,所以false,
又false,所以false即为二面角false的平面角,………………8分
所以false,因为false底面false,false平面false,所以false,
在false中,false,false,所以false.
因为false,所以false为棱false的中点,故false,
于是false即为异面直线false与false所成的角.………………………………10分
易知false,false,
在false中,由余弦定理知,false,
所以异面直线false与false所成角的余弦值为false.………………………………12分
22.(1)由题意知,圆false的圆心false在直线false上,设false,半径为false,
因为圆false与圆false外切,且圆false的圆心false,半径为false,
所以false,………………………………1分
即false①
又false,即false②………………………………2分
由①得,false,代入②得,false,
解得false或false(舍),所以false,
故所求圆false的标准方程为false.………………………………4分
(2)当false的斜率不存在时,不符合题意.
当false的斜率存在时,设为false,故false的方程为false,
因为false被两圆截得的弦长相等,
所以false,……………………………………………6分
即false,解得false或false,
故直线false的方程为false或false.…………………………………8分
(3)设false,由false可知,false,
即false,所以false,
即false,
整理得false①,…………………………………………10分
又直线false的方程为false②,…………………………………………11分
由①②联立解得,false,false或false,false,
由false,false两点不重合,故false,false不合题意,舍去,
故存在点false符合题意.………………………………………………………12分
高一年级数学试题
一、单项选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知点M(1,6) , N(7,3),则直线MN的斜率为
false2
2.false的值为
false
3. 圆false的圆心坐标为
false
4.下列命题错误的是
A.不在同一直线上的三点确定一个平面
B.两两相交且不共点的三条直线确定一个平面
C.如果两个平面垂直,那么其中一个平面内的直线一定垂直于另一个平面
D.如果两个平面平行,那么其中一个平面内的直线一定平行于另一个平面
5.下列叙述正确的是
A.频率是稳定的,概率是随机的
B.互斥事件一定不是对立事件,但是对立事件一定是互斥事件
C. 5张奖券中有1张有奖,甲先抽,乙后抽,那么乙比甲抽到有奖奖券的可能性小
D.若事件A发生的概率为P(A),则false
6. 在△ABC中,已知∠B=60°,边AB=4,且△ABC的面积为2,则边AC的长为
false
7. 某同学5次考试的数学成绩x与物理成绩y的统计数据如下表,已知该同学的物理成绩)与数学成绩x是线性相关的,根据数据可得回归方程false的b的值为0.5,则当该生的物理成绩y达到90分时,可以估计他的数学成绩为
А. 140
B. 142
C. 145
2620010194310D. 148
8. 阿基米德(Archimedes,公元前287年一公元前212年)是古希腊伟大的数学家、物理学家和天文学家.他推导出的结论“圆柱内切球体的体积是圆柱体积的三分之二,并且球的表面积也是圆柱表面积的三分之二”是其毕生最满意的数学发现,后人按照他生前的要求,在他的墓碑上刻着一个圆柱容器里放了一个球,如图,该球顶天立地,四周碰边,圆柱的底面直径与高都等于球的直径,若球的体积为36π,则圆柱的表面积为
A. 36π
B. 45π
C. 54π
D. 63π
二、多项选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得3分,有选错的得0分。
9. 已知直线false,则下列说法正确的是
A.若false,则m=-1或m=3
B.若false,则m=3
C.若false,则false
D.若false,则false
10.已知△ABC的内角A, B, C所对的边分别为a, b, c,则下列说法正确的是
A.若sinB>sinC,则B>C
B.若a=4, b=2, A=,则三角形有两解
C.若bcosB-ccosC=0,则△ABC一定为等腰直角三角形
D.若bcosC-ccosB—0,则△ABC一定为等腰三角形
11. PM2.5是衡量空气质量的重要指标,下图是某地7月1日到10日的PM2.5日均值(单位: ug/m3)的折线图,则下列关于这10天中PM2.5日均值的说法正确的是
A.众数为30
B.中位数是31
C.平均数小于中位数
D.后4天的方差小于前4天的方差
12.如图,在棱长为1的正方体中,下列结论正确的是
A.异面直线AC与BC1所成的角为60°
51625500B.直线AB1与平面ABC1D1所成角为45°
C.二面角false的正切值为
D.四面体false的外接球的体积为false
三、填空题:本题共4小题,每小题5分,共20分。
13.已知tanα=2, tanβ=-1,则tan(α-β)的值为________
14.过圆false上一点P(1,-2)的圆的切线的一般式方程为________
45529501313815right444515.在我国,每年的农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽粒,俗称“粽子”,古称“角黍”,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图,平行四边形形状的纸片是由六个边长为2的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为________
16.如图,某数学学习兴趣小组的同学要测量学校地面上旗杆CD的高度(旗杆CD垂直于地面),设计如下的测量方案:先在地面选定距离为30米的A, B两点,然后在A处测得false,在B处测得false,由此可得旗杆CD的高度为________米
四、解答题:本题6小题,共70分。解答应写出文字说明、证明过程或演算步骤.
17, (本小题满分10分)
已知 A(3, 2) 和false.
(1)求过点A且与直线l平行的直线方程;
(2)求点A关于直线l的对称点B的坐标.
18.(本小题满分12分)
已知false
(1)求cosα的值;
(2)求sin2α的值.
19. (本小题满分12分)
已知△ABC的内角A, B, C所对的边分别为a, b, c, A=,________且b=,请从false这三个条件中任选一个补充在横线上,求出此时△ABC的面积.
20. (本小题满分12分)
手机支付也称为移动支付(Mobile Payment),是当今社会比较流行的一种付款方式.某金融机构为了了解移动支付在大众中的熟知度,对15—65岁的人群作了问题为“你会使用移动支付吗?”的随机抽样调查,把回答“会”的100个人按照年龄分成5组,绘制成如图所示的频率分布表和频率分布直方图.
41592501601470 (1)求x,a的值;
(2)若从第1, 3组中用分层抽样的方法抽取5人,
求两组中分别抽取的人数;
(3)在(2)抽取的5人中再随机抽取2人,
求所抽取的2人来自同一个组的概率
21. (本小题满分12分)
如图,在P—ABC中, PA⊥面ABC, PA=2, CA=CB=AB=2, D为棱AB的中点,点E在棱PA上.
(1)若AE=EP,求证: PB∥平面CDE;
(2)求证:平面PAB⊥平面CDE;
39878000(3)若二面角B—CD—E的大小为120°,
求异面直线PC与DE所成角的余弦值.
22. (本小题满分12分)
如图,在平面直角坐标系xOy中,已知圆M: false,过点O及点A(-2,0)的圆N与圆M外切.
(1)求圆N的标准方程;
(2)若过点A的直线l被两圆截得的弦长相等,求直线l的方程;
(3)直线MN上是否存在点B,使得过点B分别作圆M与圆N的切线,切点分别为P, Q (不重合),满足BQ=2BP?若存在,求出点B的坐标,若不存在,请说明理由.
2019~2020学年度第二学期期末抽测
高一年级数学试题参考答案及评分标准
一、单项选择题:本题共8小题,每小题5分,共40分。
1.B 2.D 3.B 4.C 5.D 6.C 7.A 8.C
二、多项选择题:本题共4小题,每小题5分,共20分。
9.BD10.ABD11.AD 12.ACD
三、填空题:本题共4小题,每小题5分,共20分。
13.false14.false15.false16.false;false
四、解答题:本题6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17. (1)设所求直线的方程为false,将点false代入,得false,
故所求直线的方程为false.……………………………………………4分
(2)设false,则由false及线段false的中点在直线false上可得,
false…………………………………………………………8分
解得false,false,
所以点false的坐标为false.……………………………………………………10分
18.(1)因为false,所以false,所以false,
由false,所以false,
所以false
false.………………………………………6分
(2)false
false
false.………………………………………12分
19.情形一:若选择①false,
由余弦定理false,……………………………………2分
因为false,所以false; …………………………………………………………4分
情形二:若选择②false,则false,
因为false,所以false,……………………………………………………2分
因为false,所以false;………………………………………………………4分
情形三:若选择③false,则false,
所以false,………………………………………………………………2分
因为false,所以false,所以false,所以false;………4分
由正弦定理false,得false,……………………6分
因为false,false,所以false,………………………………8分
所以false,……10分
所以false.…………………12分
20.(1)由题意可知,false,…………………………………………2分
所以false,
从而false.…………………………………………………………4分
(2)第1,3组共有50人,所以抽取的比例是false,
则从第1组抽取的人数为false,……………………………………………6分
从第3组抽取的人数为false.……………………………………………8分
(3)设第1组抽取的2人为false,false,第3组抽取的3人为false,false,false,
则从这5人中随机抽取2人有如下种情形:
false,false,false,false,false,false,false,false,false,
false共有10个基本事件.………………………………………………………10分
其中符合“抽取的2人来自同一个组”的基本事件有false,false,false,
false共4个基本事件,
所以抽取的2人来自同一个组的概率false.………………………………12分
21.(1)由false知,false为棱false的中点,又因为false为棱false的中点,
所以在false中,false,因为false平面false,false平面false,
所以false平面false.………………………………………………………………2分
(2)因为false底面false,false平面false,所以false,
在false中,false,false为false的中点,所以false,
又因为false,false平面false,false平面false,
所以false平面false.………………………………………………………5分
又因为false平面false,所以平面false平面false.…………………………6分
(3)由题意知,二面角false的大小为false,
由(2)的证明可知,false平面false,又因为false平面false,所以false,
又false,所以false即为二面角false的平面角,………………8分
所以false,因为false底面false,false平面false,所以false,
在false中,false,false,所以false.
因为false,所以false为棱false的中点,故false,
于是false即为异面直线false与false所成的角.………………………………10分
易知false,false,
在false中,由余弦定理知,false,
所以异面直线false与false所成角的余弦值为false.………………………………12分
22.(1)由题意知,圆false的圆心false在直线false上,设false,半径为false,
因为圆false与圆false外切,且圆false的圆心false,半径为false,
所以false,………………………………1分
即false①
又false,即false②………………………………2分
由①得,false,代入②得,false,
解得false或false(舍),所以false,
故所求圆false的标准方程为false.………………………………4分
(2)当false的斜率不存在时,不符合题意.
当false的斜率存在时,设为false,故false的方程为false,
因为false被两圆截得的弦长相等,
所以false,……………………………………………6分
即false,解得false或false,
故直线false的方程为false或false.…………………………………8分
(3)设false,由false可知,false,
即false,所以false,
即false,
整理得false①,…………………………………………10分
又直线false的方程为false②,…………………………………………11分
由①②联立解得,false,false或false,false,
由false,false两点不重合,故false,false不合题意,舍去,
故存在点false符合题意.………………………………………………………12分
同课章节目录
