人教版数学八年级上册 第十四章 整式的乘法与因式分解 14.2 乘法公式 14.2.2 完全平方公式 同步学案(练习含答案)
文档属性
| 名称 | 人教版数学八年级上册 第十四章 整式的乘法与因式分解 14.2 乘法公式 14.2.2 完全平方公式 同步学案(练习含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 200.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-17 23:12:09 | ||
图片预览



文档简介
14.2.2
完全平方公式
一、新课导入
1.导入课题:
一块边长为a米的正方形实验田,因实际需要将其边长增加b米,形成四块实验田,以种植不同的新品种.(如图)
用不同的形式表示实验田的总面积,并进行比较.你发现了什么呢?
2.学习目标:
(1)能用符号和文字表述完全平方公式.
(2)能运用完全平方公式解题.
(3)体验归纳添、去括号法则.
3.学习重、难点:
重点:完全平方公式及应用及添、去括号法则.
难点:完全平方公式的几何意义的理解.
二、分层学习
第一层次学习
1.自学指导:
(1)自学内容:探究完全平方公式.
(2)自学时间:8分钟.
(3)自学方法:计算、比较分析、猜想结论.
(4)探究提纲:
①计算下列多项式的积,观察它们的算式形式与运算结果有什么规律.
a.(p+1)2=(p+1)(p+1)=p2+2p+1;
b.(m+2)2=m2+4m+4;
c.(2a+1)2=4a2+4a+1;
d.(2x-3)2=4x2-12x+9.
②猜想:根据你发现的规律,你能直接写出(a+b)2
的计算的结果是a2+2ab+b2,(a-b)2的结果是a2-2ab+b2.
③下列等式正确吗?若不对,对比②中发现的规律找出错在什么地方?
(x-3)2=x2-9(2m+1)2=4m2+1
都不对,都漏掉完全平方公式的“中间项”.
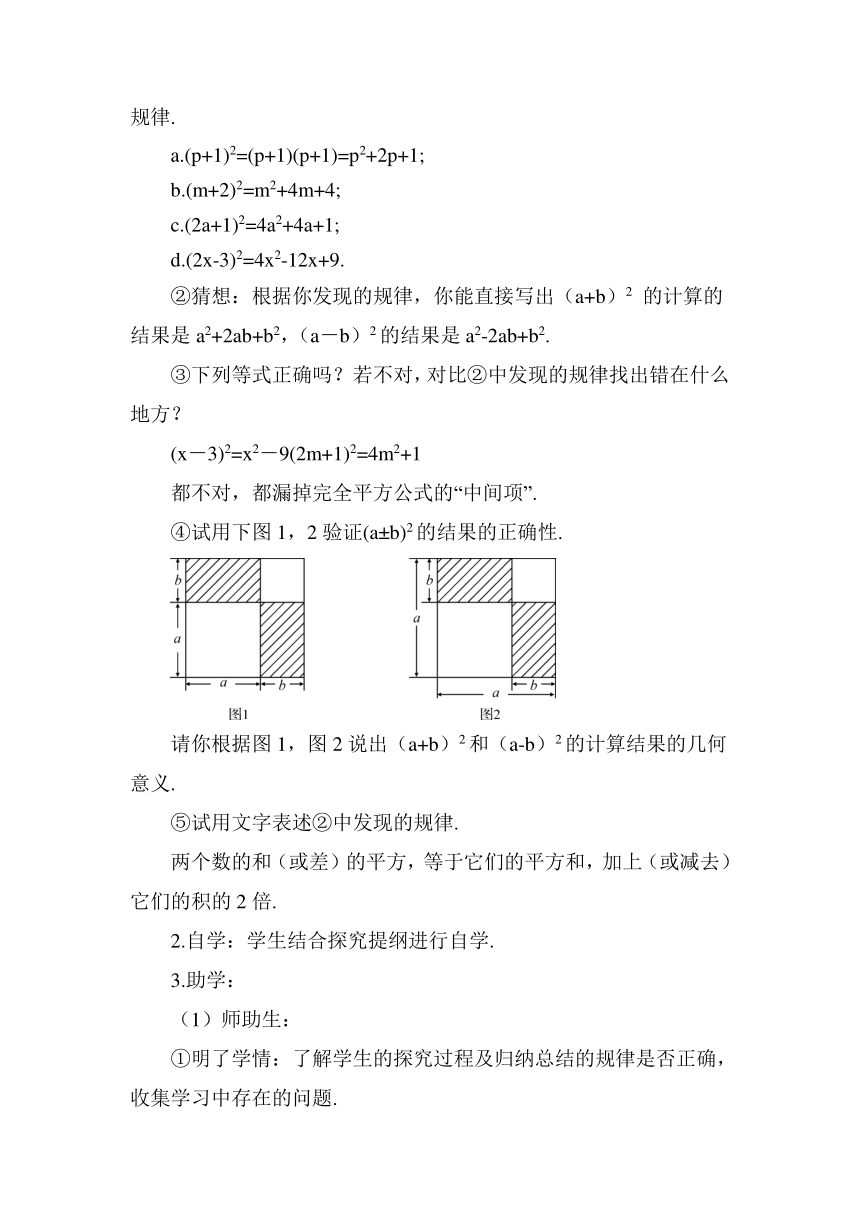
④试用下图1,2验证(a±b)2的结果的正确性.
请你根据图1,图2说出(a+b)2和(a-b)2的计算结果的几何意义.
⑤试用文字表述②中发现的规律.
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
2.自学:学生结合探究提纲进行自学.
3.助学:
(1)师助生:
①明了学情:了解学生的探究过程及归纳总结的规律是否正确,收集学习中存在的问题.
②差异指导:教师询问个别学生从探究中如何总结规律并表述规律及如何借助图1、2验证猜想.
(2)生助生:学生之间相互交流帮助.
4.强化:
(1)总结交流:公式的特点.等号左边等号右边符号特征
(2)先用公式计算下列各题,再用多项式乘法法则验证.
①(2x-3)2;②(x+y)2;③(m+2n)2;④(2x-4)2
解:①4x2-12x+9
②x2+2xy+y2
③m2+4mn+4n2
④4x2-16x+16
第二层次学习
1.自学指导:
(1)自学内容:教材第110页例3、例4.
(2)自学时间:8分钟.
(3)自学方法:认真观察例题中如何运用公式,分清题目中相当于公式中a、b的数或式是什么.
(4)自学参考提纲:
①式子(4m+n)2中,4m看作公式中的a,n看作公式中的b,所以(4m+n)2=(4m+n)(4m+n)=16m2+8mn+n2.
②(y-)2=y2-2·y·()+=y2-y+.
③因为102=100+2,所以1022=(100+2)2=(100)2+2×100×2+(2)2=10404.
④怎样计算9982?说说你的想法.
用完全平方公式,将998写成1000-2,则
9982=(1000-2)2=10002-2×1000×2+22=996004.
2.自学:学生可结合自学指导进行自学.
3.助学:
(1)师助生:
①明了学情:了解学生是否从例题中学会正确运用公式的思考过程.
②差异指导:帮助学困生对照公式怎样确定“a”、“
b”.
(2)生助生:完成自学提纲,同组内互相检查、交流帮助纠错.
4.强化:
(1)应用公式时,先确定公式中的“a”、“b”是什么?
(2)运用完全平方公式计算:①(-x-y)2;②(2y-)2
解:①x2+2xy+y2;②4y2-y+.
(3)思考:(a+b)2与(-a-b)2相等吗?(a-b)2与(b-a)2相等吗?为什么?
相等.相等.因为互为相反数的数或式子平方相等.
第三层次学习
1.自学指导:
(1)自学内容;教材第111页例5上面的内容.
(2)自学时间:5分钟.
(3)自学方法:认真看课本,并结合自学参考提纲进行学习,注意添加括号时,括号前面是正号和负号时,括号内各项符号的变化.
(4)自学参考提纲:
①整式中添加括号的依据是什么?
②添括号法则是怎样的?
③如何验证你添括号的正确性?
④在等号右边的括号内填上适当的项.
a+b-c=a+(b-c);a+b-c=a-(c-b);a-b+c=a-(b-c)
a-b-c=a-(b+c);a+b+c=a-(-b-c);a+2b-6c=a+2(b-3c).
2.自学:学生可结合自学提纲进行自学.
3.助学:
(1)师助生:
①明了学情:了解学生对添括号法则是否学会,会不会检验添括号的正确性.
②差异指导:对学生进行个别指导:括号前为负号时,添括号后注意什么.
(2)生助生:学生之间相互指导.
4.强化:
(1)添括号法则.
(2)括到括号内的各项符号的变与不变与什么有关.
(3)注意各项都变或都不变的意思.
(4)判断下列运算是否正确,若不正确,请改正过来.
①2a-b-=2a-(b-)②m-3n+2a-b=m+(3n+2a-b)
③2x-3y+2=-(2x+3y-2)④a-2b-4c+5=(a-2b)-(4c+5)
解:①不正确,应等于2a-b+
②不正确,应等于m-(3n-2a+b)
③不正确,应等于-(-2x+3y-2)
④不正确,应等于(a-2b)-(4c-5)
第四层次学习
1.自学指导:
(1)自学内容;教材第111页例5的内容.
(2)自学方法:认真看教材,注意观察多项式相乘的特点,以便合理地添括号选用相应的公式.
(3)自学参考提纲:
①计算(x+2y-3)(x-2y+3)时,第一步将整式变形为[x+(2y-3)][x-(2y-3)],目的是什么?本题计算过程中,先后运用了几个公式?本题对应用公式计算有何启示?
②计算(a+b+c)2时,例题是写成[(a+b)+
c]2,把a+b当作完全平方式中的a,把c当作完全平方式中的b,还有没有其它的添括号的方法计算本题,试试吧!
③运用乘法公式计算(1)(a+2b-1)2;(2)(2x+y+z)(2x-y-z).
解:(1)原式=(a+2b)2-2(a+2b)+12
=a2+4ab+4b2-2a-4b+1;
(2)原式=[2x+(y+z)][2x-(y+z)]=4x2-(y+z)2=4x2-y2-2yz-z2.
2.自学:学生结合自学指导进行自学.
3.助学:
(1)师助生:
①明了学情:了解学生是否灵活运用添括号的法则添加括号,并运用完全平方公式计算.
②差异指导:对学生学习过程中存在的问题予以分类指导.
(2)生助生:学生之间相互交流帮助.
4.强化:
(1)总结交流:在乘法运算时,一定要观察多项式的特点,选用对应的公式进行运算.
(2)添括号法则是去括号法则反过来得到的,无论是添括号,还是去括号,运算前后代数式的值都保持不变,所以我们可以用去括号法则验证所添括号是否正确.
(3)练习:计算
①(a+b+1)(a+b-1);
②(2x-y-3)2.
解:①原式=a2+2ab+b2-1;
②原式=(2x)2-2x·(y+3)+(y+3)2=4x2-2xy-6x+y2+6y+9
三、评价
1.学生的自我评价(围绕三维目标):学生代表交流自己的学习收获和学习体会.
2.教师对学生的评价:
(1)表现性评价:对学生的学习态度、方法、收效及不足进行点评.
(2)纸笔评价:课堂评价检测.
3.教师的自我评价(教学反思):
本课时教学重点是引导学生观察分析完全平方公式的结构特征,教师可组织学生独立观察,再在小组内交流,最后由教师归纳评点,以便学生认识与完全平方公式相关的所有变式.
针对性练习
一、基础巩固(第1、2、3、4、5题每题8分,第6题20分,共60分)
1.(-3x-1)2=9x2+6x+1;
(-2x+5)2=4x2-20x+25;
2.(x-y-1)2=x2+y2-x-xy+2y+1;
(x-y)2=x2-xy+y2.
3.(x+y)2-4xy=(x-y)2
99.82=(100-0.2)2=9960.04
4.(1)若(x-5)2=x2+kx+25,则k=-10;
(2)若4x2+mx+9是完全平方式,则m=12.
5.下列各式中,与(x-1)2相等的是(B)
A.x2-1
B.x2-2x+1
C.x2-2x-1
D.x2
6.利用乘法公式计算:
(1)(a-b+2c)2;
(2)(-2x-y)2;
(3)(x+y-z)(x-y+z);(4)(a+b+c)2-(a-b-c)2.
解:(1)原式=a2+b2+4c2-2ab+4ac-4bc;
(2)原式=4x2+4xy+y2;
(3)原式=x2-(y-z)2=x2-y2+2yz-z2;
(4)原式=(a+b+c+a-b-c)(a+b+c-a+b+c)=2a·(2b+2c)=4ab+4ac
二、综合应用(每题10分,共20分)
7.化简求值:[2x2-(x+y)(x-y)][(-x-y)(y-x)+2y2],其中x=1,y=2.
解:原式=(2x2-x2+y2)(x2-y2+2y2)
=(x2+y2)2=x4+2x2y2+y4
当x=1,y=2时,原式=1+8+16=25.
8.已知a+b=-7,ab=12,求a2+b2-ab和
(a-b)2的值.
解:a2+b2-ab=(a+b)2-3ab=(-7)2-3×12=13.
(a-b)2=(a+b)2-4ab=(-7)2-4×12=1.
三、拓展延伸(每题10分,共20分)
9.已知a+b-c=5,a-b+c=-3,求a2-b2+2bc-c2的值.
解:a2-b2+2bc-c2=a2-(b-c)2=(a+b-c)(a-b+c)
=5×(-3)=-15.
10.已知x+=2,求x2+和x-的值.
解:(x+)2=
x2++2=4
∴x2+=2,
∴x2+-2=0,
∴(x-)2=0,
∴x-=0.
完全平方公式
一、新课导入
1.导入课题:
一块边长为a米的正方形实验田,因实际需要将其边长增加b米,形成四块实验田,以种植不同的新品种.(如图)
用不同的形式表示实验田的总面积,并进行比较.你发现了什么呢?
2.学习目标:
(1)能用符号和文字表述完全平方公式.
(2)能运用完全平方公式解题.
(3)体验归纳添、去括号法则.
3.学习重、难点:
重点:完全平方公式及应用及添、去括号法则.
难点:完全平方公式的几何意义的理解.
二、分层学习
第一层次学习
1.自学指导:
(1)自学内容:探究完全平方公式.
(2)自学时间:8分钟.
(3)自学方法:计算、比较分析、猜想结论.
(4)探究提纲:
①计算下列多项式的积,观察它们的算式形式与运算结果有什么规律.
a.(p+1)2=(p+1)(p+1)=p2+2p+1;
b.(m+2)2=m2+4m+4;
c.(2a+1)2=4a2+4a+1;
d.(2x-3)2=4x2-12x+9.
②猜想:根据你发现的规律,你能直接写出(a+b)2
的计算的结果是a2+2ab+b2,(a-b)2的结果是a2-2ab+b2.
③下列等式正确吗?若不对,对比②中发现的规律找出错在什么地方?
(x-3)2=x2-9(2m+1)2=4m2+1
都不对,都漏掉完全平方公式的“中间项”.
④试用下图1,2验证(a±b)2的结果的正确性.
请你根据图1,图2说出(a+b)2和(a-b)2的计算结果的几何意义.
⑤试用文字表述②中发现的规律.
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
2.自学:学生结合探究提纲进行自学.
3.助学:
(1)师助生:
①明了学情:了解学生的探究过程及归纳总结的规律是否正确,收集学习中存在的问题.
②差异指导:教师询问个别学生从探究中如何总结规律并表述规律及如何借助图1、2验证猜想.
(2)生助生:学生之间相互交流帮助.
4.强化:
(1)总结交流:公式的特点.等号左边等号右边符号特征
(2)先用公式计算下列各题,再用多项式乘法法则验证.
①(2x-3)2;②(x+y)2;③(m+2n)2;④(2x-4)2
解:①4x2-12x+9
②x2+2xy+y2
③m2+4mn+4n2
④4x2-16x+16
第二层次学习
1.自学指导:
(1)自学内容:教材第110页例3、例4.
(2)自学时间:8分钟.
(3)自学方法:认真观察例题中如何运用公式,分清题目中相当于公式中a、b的数或式是什么.
(4)自学参考提纲:
①式子(4m+n)2中,4m看作公式中的a,n看作公式中的b,所以(4m+n)2=(4m+n)(4m+n)=16m2+8mn+n2.
②(y-)2=y2-2·y·()+=y2-y+.
③因为102=100+2,所以1022=(100+2)2=(100)2+2×100×2+(2)2=10404.
④怎样计算9982?说说你的想法.
用完全平方公式,将998写成1000-2,则
9982=(1000-2)2=10002-2×1000×2+22=996004.
2.自学:学生可结合自学指导进行自学.
3.助学:
(1)师助生:
①明了学情:了解学生是否从例题中学会正确运用公式的思考过程.
②差异指导:帮助学困生对照公式怎样确定“a”、“
b”.
(2)生助生:完成自学提纲,同组内互相检查、交流帮助纠错.
4.强化:
(1)应用公式时,先确定公式中的“a”、“b”是什么?
(2)运用完全平方公式计算:①(-x-y)2;②(2y-)2
解:①x2+2xy+y2;②4y2-y+.
(3)思考:(a+b)2与(-a-b)2相等吗?(a-b)2与(b-a)2相等吗?为什么?
相等.相等.因为互为相反数的数或式子平方相等.
第三层次学习
1.自学指导:
(1)自学内容;教材第111页例5上面的内容.
(2)自学时间:5分钟.
(3)自学方法:认真看课本,并结合自学参考提纲进行学习,注意添加括号时,括号前面是正号和负号时,括号内各项符号的变化.
(4)自学参考提纲:
①整式中添加括号的依据是什么?
②添括号法则是怎样的?
③如何验证你添括号的正确性?
④在等号右边的括号内填上适当的项.
a+b-c=a+(b-c);a+b-c=a-(c-b);a-b+c=a-(b-c)
a-b-c=a-(b+c);a+b+c=a-(-b-c);a+2b-6c=a+2(b-3c).
2.自学:学生可结合自学提纲进行自学.
3.助学:
(1)师助生:
①明了学情:了解学生对添括号法则是否学会,会不会检验添括号的正确性.
②差异指导:对学生进行个别指导:括号前为负号时,添括号后注意什么.
(2)生助生:学生之间相互指导.
4.强化:
(1)添括号法则.
(2)括到括号内的各项符号的变与不变与什么有关.
(3)注意各项都变或都不变的意思.
(4)判断下列运算是否正确,若不正确,请改正过来.
①2a-b-=2a-(b-)②m-3n+2a-b=m+(3n+2a-b)
③2x-3y+2=-(2x+3y-2)④a-2b-4c+5=(a-2b)-(4c+5)
解:①不正确,应等于2a-b+
②不正确,应等于m-(3n-2a+b)
③不正确,应等于-(-2x+3y-2)
④不正确,应等于(a-2b)-(4c-5)
第四层次学习
1.自学指导:
(1)自学内容;教材第111页例5的内容.
(2)自学方法:认真看教材,注意观察多项式相乘的特点,以便合理地添括号选用相应的公式.
(3)自学参考提纲:
①计算(x+2y-3)(x-2y+3)时,第一步将整式变形为[x+(2y-3)][x-(2y-3)],目的是什么?本题计算过程中,先后运用了几个公式?本题对应用公式计算有何启示?
②计算(a+b+c)2时,例题是写成[(a+b)+
c]2,把a+b当作完全平方式中的a,把c当作完全平方式中的b,还有没有其它的添括号的方法计算本题,试试吧!
③运用乘法公式计算(1)(a+2b-1)2;(2)(2x+y+z)(2x-y-z).
解:(1)原式=(a+2b)2-2(a+2b)+12
=a2+4ab+4b2-2a-4b+1;
(2)原式=[2x+(y+z)][2x-(y+z)]=4x2-(y+z)2=4x2-y2-2yz-z2.
2.自学:学生结合自学指导进行自学.
3.助学:
(1)师助生:
①明了学情:了解学生是否灵活运用添括号的法则添加括号,并运用完全平方公式计算.
②差异指导:对学生学习过程中存在的问题予以分类指导.
(2)生助生:学生之间相互交流帮助.
4.强化:
(1)总结交流:在乘法运算时,一定要观察多项式的特点,选用对应的公式进行运算.
(2)添括号法则是去括号法则反过来得到的,无论是添括号,还是去括号,运算前后代数式的值都保持不变,所以我们可以用去括号法则验证所添括号是否正确.
(3)练习:计算
①(a+b+1)(a+b-1);
②(2x-y-3)2.
解:①原式=a2+2ab+b2-1;
②原式=(2x)2-2x·(y+3)+(y+3)2=4x2-2xy-6x+y2+6y+9
三、评价
1.学生的自我评价(围绕三维目标):学生代表交流自己的学习收获和学习体会.
2.教师对学生的评价:
(1)表现性评价:对学生的学习态度、方法、收效及不足进行点评.
(2)纸笔评价:课堂评价检测.
3.教师的自我评价(教学反思):
本课时教学重点是引导学生观察分析完全平方公式的结构特征,教师可组织学生独立观察,再在小组内交流,最后由教师归纳评点,以便学生认识与完全平方公式相关的所有变式.
针对性练习
一、基础巩固(第1、2、3、4、5题每题8分,第6题20分,共60分)
1.(-3x-1)2=9x2+6x+1;
(-2x+5)2=4x2-20x+25;
2.(x-y-1)2=x2+y2-x-xy+2y+1;
(x-y)2=x2-xy+y2.
3.(x+y)2-4xy=(x-y)2
99.82=(100-0.2)2=9960.04
4.(1)若(x-5)2=x2+kx+25,则k=-10;
(2)若4x2+mx+9是完全平方式,则m=12.
5.下列各式中,与(x-1)2相等的是(B)
A.x2-1
B.x2-2x+1
C.x2-2x-1
D.x2
6.利用乘法公式计算:
(1)(a-b+2c)2;
(2)(-2x-y)2;
(3)(x+y-z)(x-y+z);(4)(a+b+c)2-(a-b-c)2.
解:(1)原式=a2+b2+4c2-2ab+4ac-4bc;
(2)原式=4x2+4xy+y2;
(3)原式=x2-(y-z)2=x2-y2+2yz-z2;
(4)原式=(a+b+c+a-b-c)(a+b+c-a+b+c)=2a·(2b+2c)=4ab+4ac
二、综合应用(每题10分,共20分)
7.化简求值:[2x2-(x+y)(x-y)][(-x-y)(y-x)+2y2],其中x=1,y=2.
解:原式=(2x2-x2+y2)(x2-y2+2y2)
=(x2+y2)2=x4+2x2y2+y4
当x=1,y=2时,原式=1+8+16=25.
8.已知a+b=-7,ab=12,求a2+b2-ab和
(a-b)2的值.
解:a2+b2-ab=(a+b)2-3ab=(-7)2-3×12=13.
(a-b)2=(a+b)2-4ab=(-7)2-4×12=1.
三、拓展延伸(每题10分,共20分)
9.已知a+b-c=5,a-b+c=-3,求a2-b2+2bc-c2的值.
解:a2-b2+2bc-c2=a2-(b-c)2=(a+b-c)(a-b+c)
=5×(-3)=-15.
10.已知x+=2,求x2+和x-的值.
解:(x+)2=
x2++2=4
∴x2+=2,
∴x2+-2=0,
∴(x-)2=0,
∴x-=0.
