一次函数知识要点剖析

一次函数知识要点剖析
一、理解函数概念“五”注意
教材中是这样定义的：一般地，在一个变化过程中，如果有两个变量x与y，并且对于x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就说x是自变量，y是x的函数.
如果当x=a时y=b，那么b叫做当自变量的值为a时的函数值.
正确理解函数这一概念必须注意如下五点：
一、注意理解“在一个变化过程中，有两个变量”
函数中的两个变量，一个是自变量，另一个是函数（即因变量），其中自变量的变化才能引起函数的变化.因此，函数关系是指两个变量之间的一种特殊的对应关系，即变量x与变量y之间存在的对应关系.
例如，y = 2x - 1中的对应关系是指：因变量y对应于自变量x的2倍减去1的差 .
二、注意理解“x的每一个确定的值”
这句话有两层含义：
（1）自变量x的取值不能使对应关系无意义，如y =，x的取值不能为1；
（2）自变量x的取值不能使某个变化过程（实际问题）无意义.
三、注意理解“x的每一个确定的值，y都有唯一确定的值与其对应”
值得注意的是“y都有唯一确定的值”的含义，即有一个而且只有一个值.因此，自变量x在取值范围内的每一个确定的值，函数 y 都有一个而且只有一个值与它对应 .
如 y = ±x，这里y不是 x 的函数，因为在自变量 x每个值，y有两个值与它对应 .
或如图所示，皆不是函数关系：
四、注意正确判断“谁是谁的函数”
判断“谁是谁的函数”，即在某个函数关系中，谁是自变量，谁是函数. 在一个变化过程中，如果有两个变量，一个变量取其范围内的每一个确定的值，另一个变量都有唯一确定的值与之对应，那么这两个变量“互为函数”，即谁都可作为对方的函数.
通常，函数即因变量写在等号左边。
五、注意正确确定“自变量的取值范围”
1、自变量的取值必须使含自变量的代数式有意义
（1）整式型：其自变量的取值范围是全体实数.如函数y=3x+1，y=x2+x－4中自变量x的取值范围是全体实数.
（2）分式型：其自变量的取值范围是使得分母不为零的实数.如函数y=中变量x的取值范围是x≠1（由x－1≠0得）.
（3）二次根式型：其自变量的取值范围是使得被开方式为非负数的实数.如函数y=中自变量x的取值范围是x≥1（由x－1≥0得）.
（4）复合型：即自变量同时含有上述两种或三种情况时，自变量的取值范围是它们的公共解.如函数y=中自变量x的取值范围是x－2≥0与x－3≠0的公共解，即x≥2且x≠3.
2、自变量的取值必须使实际问题有意义
当函数关系式表示实际问题时，自变量的取值必须使实际问题有意义.
如一个正方形的边长为3cm，它的各边长减少xcm后，所得新正方形的周长为ycm.则y与x的关系式为y=12－4x, 自变量x的取值范围是0 < x < 3.
2、函数的表示方法
函数有三种表示方法：（1）列表法；（2）图象法；(3)表达式法（也称关系式或解析式）.
二、一次函数的概念、图象及其图象的性质
1、一次函数的概念
课本首先列举两例，得出两个函数关系式，从而引导归纳出一次函数的定义：若两个变量x，y间的关系式可以表示成y = kx + b（k，b为常数，k≠0）的形式，则称y是x的一次函数（x为自变量，y为因变量）.特别地，当b = 0时，称y是x的正比例函数.
〖解读〗：
（1）一次函数的表达式y = kx + b（k≠0）的结构特征：
①k≠0；②自变量x的次数是1；③常数项b可为任意数.
（2）正比例函数的表达式y = kx （k≠0）的结构特征：
①k≠0；②自变量x的次数是1，这是识别一次函数的关键；③无常数项或常数项为0.
（3）正比例函数是一次函数的特殊形式.
针对训练：
（1）已知函数y=(2m-1)x+1-3m，m为何值时，
①这个函数为正比例函数？
②这个函数是一次函数？
析解：解题过程中要注意，一次项系数2m-1不等于0．
解：①由正比例函数的定义，有1-3m=0且2m-1≠0，得，
∴时，y=(2m-1)x+1-3m为正比例函数．
②由一次函数的定义知，当且时，y=(2m-1)x+1-3m为一次函数．
（2）若函数，则m=_______。
评注：学好概念是学好数学的前提，利用数学概念是数学解题的基本方法，熟知一次函数定义中自变量x的系数、次数要求是解本类题的关键．
2、函数图象
（1）函数图象的概念：把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标，在直角坐标系内描出它的对应点，所有这些点组成的图形叫做该函数的图象.
（2）函数图象的画法：一般分为三步：①列表；②描点；③连线.
3、一次函数的图象
（1）形状：一次函数y = kx + b的图象是一条直线，所以一次函数y = kx + b的图象也称为直线y = kx + b.
（2）画法：由于一次函数y = kx + b的图象是一条直线，因此作一次函数图象时,只要确定两个点,再过这两个点作直线就可以了.
一般地，一次函数y = kx + b的图象是经过点（0，b）和（－，0）的一条直线，当b = 0时，即为正比例函数，其图象是经过原点（0，0）和点（1，k）的一条直线.
（3）性质：一次函数性质涉及面广，知识度深，是函数考核方面的重中之重，因此正确的掌握，灵活的应用，便成为了学好一次函数的重点问题。
探究一下一次函数的相关性质，一次函数y=kx+b(k、b是常数，且k≠0)的图像是一条直线，它的性质如下：
性质一：一次函数中k的取值决定了图像的倾斜方向。
①k＞0直线必然经过一、三象限，y的值随着x的增大而增大。
②k＜0直线必然经过二、四象限，y的值随着x的增大而减小。
相关链接：
1．正比例函数的图像肯定经过__________象限，同时y的值会随着x的增大而_________。
2．若一次函数的图像经过一、三象限，且，则一次函数的解析式应为_________。
答案：1.二、 四；减小。 2.
性质二：一次函数中b的取值确定直线与y轴交点的位置，反之亦然。
①b＞0直线与y的交点在x轴的上方。
②b=0直线过原点。
③b＜0直线与y的交点在x轴的下方。
相关链接：
1．已知一次函数的图像与轴相交负半轴，则图像肯定会过（ ）
A. 一、二、三象限 B. 二、三、四象限
C. 一、二、四象限 D. 一、三、四象限
2．若一次函数的图像，与轴围成的三角形面积为4，则一次函数的解析式应为_________________。
答案：1. D. 2. 或
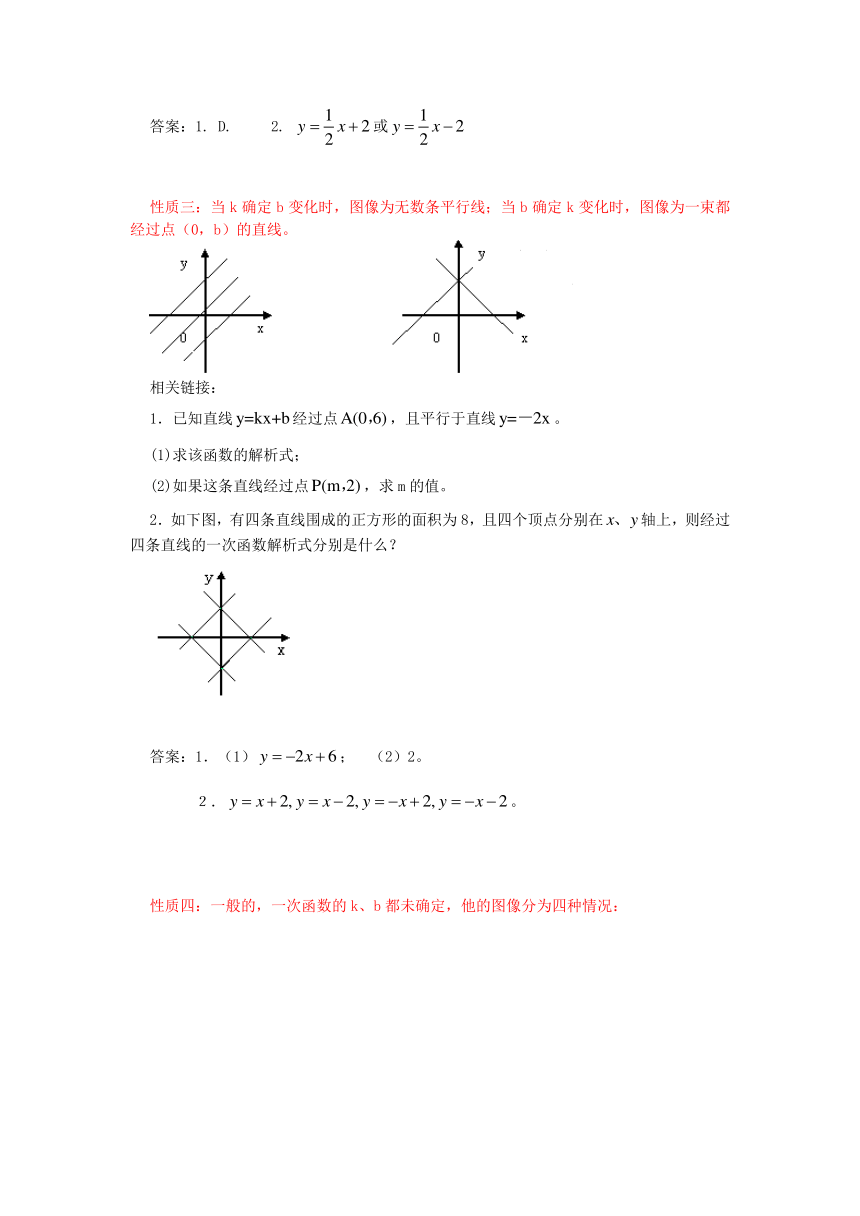
性质三：当k确定b变化时，图像为无数条平行线；当b确定k变化时，图像为一束都经过点（0，b）的直线。
相关链接：
1．已知直线经过点，且平行于直线。
(1)求该函数的解析式；
(2)如果这条直线经过点，求m的值。
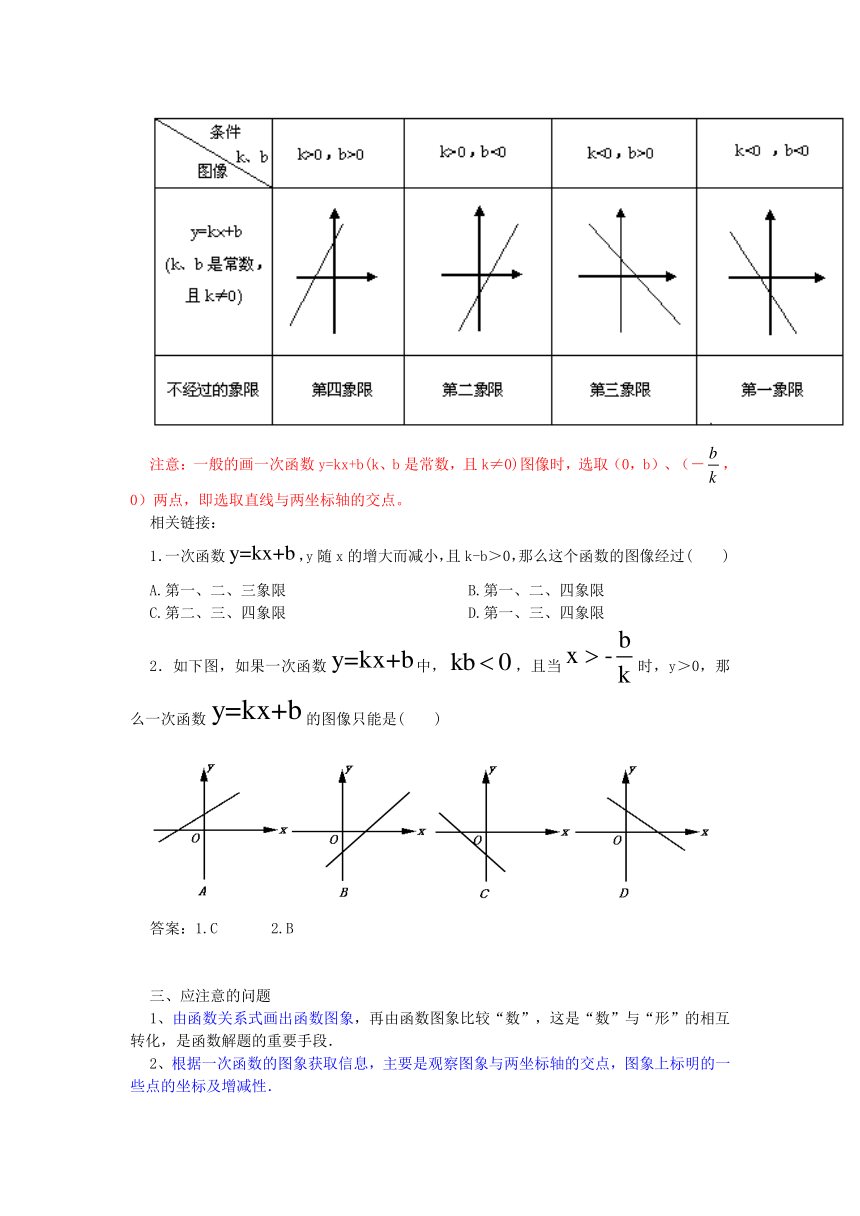
2．如下图，有四条直线围成的正方形的面积为8，且四个顶点分别在轴上，则经过四条直线的一次函数解析式分别是什么？
答案：1．（1）； （2）2。
　　 ２．。
性质四：一般的，一次函数的k、b都未确定，他的图像分为四种情况：
注意：一般的画一次函数y=kx+b(k、b是常数，且k≠0)图像时，选取（0，b）、（－，0）两点，即选取直线与两坐标轴的交点。
相关链接：
1．一次函数，y随x的增大而减小，且k-b＞0，那么这个函数的图像经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第二、三、四象限 D.第一、三、四象限
2．如下图，如果一次函数中，，且当时，y＞0，那么一次函数的图像只能是( )
答案：1.C 2.B
三、应注意的问题
1、由函数关系式画出函数图象，再由函数图象比较“数”，这是“数”与“形”的相互转化，是函数解题的重要手段．
2、根据一次函数的图象获取信息，主要是观察图象与两坐标轴的交点，图象上标明的一些点的坐标及增减性．
四、一次函数表达式的确定
1、方法：
待定系数法：先设出式子中的未知数，再根据条件求出未知系数，从而写出这个式子的方法叫做待定系数法，其中未知数的系数也叫做待定系数.
2、步骤：（1）设出含有待定系数的一次函数表达式（正比例函数设y = kx；一次函数设y = kx + b）；
（2）把已知条件（自变量与因变量的对应值）代入表达式，得到关于待定系数的方程（组）；
（3）解方程（组），求出待定系数；
（4）将求得的待定系数的值代回所设的表达式.
　　确定一次函数的表达式，就是确定式中所含的未知系数的值，有时这个未知数需要我们设定，主要的解题思路是解方程．
　　（一）确定正比例函数与一次函数的表达式应具备的条件：
　　1．由于正比例函数中只有一个未知系数k，故只要一个条件，即一对x，y的值或一个点的坐标，就可以求出k的值，确定正比例函数的表达式．
　　2．一次函数是有两个未知系数k，b，需要两个独立的关于k，b的条件，求得k， b的值，这两个条件通常是两个点的坐标或两对x，y的值．
　　（二）正比例函数与一次函数表达式的确定方法：
　　1．对于正比例函数，将一个已知点的纵、横坐标代入中，解一元一次方程，求出k就能确定它的表达式．
　　例1　一个正比例函数的图象经过点A（-2，4），写出这个正比例函数的表达式．
　　析解：把点A的纵、横坐标代入表达式中，即其中的，即，解得，所以，函数的表达式为：．
　　2．对于一次函数，将两个已知点的纵、横坐标分别代入中，建立关于k，b的两个方程，求出k，b的值，就能确定函数的表达式．
　　例2　直线经过点A（-3，0）和点B（0，2），求这条直线的表达式．
　　析解：本题的确定方法为：把点A和点B的横、纵坐标分别当作x，y的值代入中，可得两个方程：，得出，，从而得出直线的表达式为：．
总结：若直线与坐标轴分别交于（m，0），（0，n）点，则
　　
3．如果题中没有给出函数的表达式，首先要设出表达式，再根据已知条件求出未知数的值．
　　
例3　已知一次函数的图象经过点（0，1）和（-1，-3），求它的表达式．
　　析解：本题并没有给出一次函数的表达式，需要我们设出来，可设这个一次函数的表达式为（），然后将点的坐标代入其中，仿照上面的方法可得，此函数的表达式为：．
　　（三）两个特殊的确定方法：
　　1．根据交点确定：由题目中的已知条件，找出对解决问题有用的条件．
　　例4　已知一个一次函数的图象和直线与y轴相交于同一点，且过点（2，-6），求此一次函数的表达式．
　　析解：如果设要求的一次函数的表达式为（），因为直线与y轴的交点为（0，2），易知其中的未知数，再根据另一条件求得，所以此函数的表达式为：．
　　2．由平行线确定：如果两条直线平行，那么表示这两条直线的表达式中的“k”值相等，在解题时要注意这个“隐含条件”．
　　例5　若直线平行于直线，且过点（5，-9），求直线的表达式．
　　析解：直接可得，再将已知点的坐标代入求出，所以，此函数的表达式为：．
（四）与已知一次函数对称
例6.已知某一次函数的图像与直线关于x轴对称，求此一次函数解析式．
解：由于两一次函数图像关于x轴对称，则直线上的点A(x，y)关于x轴的对称点A′(x，－y)必在所求函数的图像上，即两函数自变量取值相同时，函数值恰好互为相反数，故所求函数解析式为，整理得．
评析：由一次函数图像的特征可知，若两函数及的图像关于x轴对称，则必有，仿照此法，也可以求两函数的图像关于y轴对称时的解析式．
（五）由已知函数平移所得
例7.将直线向上平移5个单位，求所得图像的解析式．
解：设所求函数关系式为，因为平移后两函数图像互相平行，故有k=3，而b=－2+5=3，故所求函数解析式为．
评析：一般地，对于一次函数（k≠0），若将其向上平移m个单位，则所得函数解析式为；若将其向下平移m个单位，则所得函数解析式为（特别，当m=b时平移后的函数图象将通过原点而转变成正比例函数）．
五、一次函数的应用
1、由函数图象获取信息
（1）从函数图象的形状可判断函数是否是一次函数；
（2）从x轴、y轴的实际意义去理解图象上点的坐标的实际意义.
2、利用一次函数的知识解应用问题的一般步骤：
（1）设定实际问题中的变量；
（2）建立一次函数关系式；
（3）确定自变量的取值范围，保证自变量具有实际意义；
（4）解答一次函数问题，如极值、合算等；
（5）写出答案.
【典题举例】
例1点A(2，4)在正比例函数的图象上，这个正比例函数的解析式是　　　　　.
解析：由这个正比例函数的解析式为：y = kx.
当x =2时，y =4，即4=2 k，则k = 2.
故这个正比例函数的解析式为y =2x.
例2一次函数y=kx+3的图象与坐标轴的两个交点之间的距离为5，则k的值为 .
解析：设一次函数y=kx+3的图象与x轴、y轴分别相交于A、B两点.由题意，得
当x=0时，y=3；当y=0时，x=－.
则OA=3，OB=.
在Rt△AOB中，由勾股定理，得
OA2＋OB2=AB2，即32＋（）2=52，
解得，k=±.
例3一根蜡烛长20cm，点燃后每小时燃烧5cm，燃烧时剩下的长度为y(cm)与燃烧时间x（小时）的函数关系用图象表示为下图中的（　　）
解析：由题意，得
y与x的函数关系式：y=－5x＋20（0≤x≤4）
故应选A.
例4已知一次函数的图象经过A（－2，－3），B（1，3）两点.
（1）求这个一次函数的解析式；
（2）试判断点P（－1，1）是否在这个一次函数的图象上？
解析：设这个一次函数的解析式为y = kx + b. 由题意，得
解得，k =2，b = 1.
故这个一次函数的解析式为y = 2x +1.
（2）当x=－1时，y = 2x +1=2×（－1）＋1=－1.
所以点P（－1，1）不在这个一次函数的图象上.
例5某洗衣机在洗涤衣服时，经历了进水、清洗、排水、脱水四个连续过程，其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示：
根据图象解答下列问题：
（1）洗衣机的进水时间是多少分钟？清洗时洗衣机中的水量是多少升？
（2）已知洗衣机的排水速度为每分钟19升， ①求排水时y与x之间的关系式；②如果排水时间为2分钟，求排水结束时洗衣机中剩下的水量.
解析：（1）由图象可知，洗衣机的进水时间是4分钟，清洗时洗衣机中的水量是40升.
（2）①由题意，得y=40－19x；
②当x =2时，y=40－19x=40－19×2=2.
故洗衣机中剩下的水量2升.
一次函数易错问题剖析
一次函数是初中数学的重要内容之一，利用一次函数的有关知识解题时，由于忽略限制条件、考虑问题不全面或受思维定势的影响会出现这样那样的错误，下面给出归类剖析，供同学们在学习时参考。
忽略定义式中的限制条件出错。
例1、已知函数是一次函数，则n=＿＿＿。
错解：因为是一次函数，所以　　解得： 或
剖析：一次函数的定义式为：一般地，形如（k ,b是常数，）的函数，叫做一次函数，本题正是因为忽略了这一限制条件而出错。
正解：因为是一次函数，　
　　　所以　　解得　　　所以
忽略坐标系中表示线段的长时要取点的坐标的绝对值。
例2、已知一次函数的图象经过点A（0，2）且与坐标轴围成的直角三角形面积为4，则这个一次函数的解析式为＿＿＿＿。
错解：设一次函数的解析式为　，因为函数的图象经过点A（0，2），所以b=2，所以函数的解析式为，求这个函数图象与x轴的交点，即解方程组　　解得　，　即图象与x轴交点坐标为　　由三角形的面积公式得　　　解得：　 　　所以这个一次函数的解析式为
剖析：在表示三角形的面积时，用的是三角形的边长，是线段的长度，不要忽略要取绝对值才能表示线段的长度，否则就会漏掉一个解，本题正是因为忽略了这点而出了错。
正解：设一次函数的解析式为　，因为函数的图象经过点A（0，2），所以b=2，所以函数的解析式为，求这个函数图象与x轴的交点，即解方程组　　解得　，　即图象与x轴交点坐标为　　由三角形的面积公式得　　　解得：　所以这个一次函数的解析式为　，　或　。
考虑问题不全面出错。
例3、一次函数，当时，对应的函数值为，求k+b的值。
错解：因为当时，对应的函数值为
所以当时　　当时
所以可得方程组　　解得　　　所以
剖析：由于问题中没有给出y随x的变化怎样变化，所以应该考虑到有可能y随x的增大而增大，也有可能y随x的增大而减小，本题的出错原因正是没有全面考虑到这一点而漏解出错。
正解：若y随x的增大而增大时，则当时　　当时
　　　所以可得方程组　　解得　　　所以
　　　若y随x的增大而减小时，则当时　　当时
　　　所以可得方程组　　解得　　所以
　　　所以k+b的值是9或1
一次函数图象与直线两者关系不清出错。
例4、已知直线不经过第二象限，则m的取值范围是＿＿＿。
错解：有题意可得，直线经过一、三、四象限或一、三象限
所以可得　　　解得
剖析：因为直线　当时　图象也不经过第二象限，所以也符合条件，以上的错解忽略了直线图象不过第二象限这一情况导致了错解。
正解：有题意可得，直线经过一、三、四象限或一、三象限
所以可得　　　解得　　特别地当时也符合题意，所以　
实际问题需画图象时，容易忽略自变量的取值范围而出错。
例5、已知等腰三角形的周长为20，把底边y表示为腰长x的函数，并画出图象。
错解：因为等腰三角形底边长为y　，　腰长为x　，周长为20
所以　　所以
令得　　所以点A（0，20）
　　　令得　　所以点B（10，0）
所以经过A，B的直线即为的图
象，如图1所示　 . 　　　　　　　　　　　　　　　　　　　　 图1
剖析：本题是实际问题，x和y分别表示线段的长的实际意义，x表示等腰三角形的腰长，y表示底边长，x和y应该满足三角形的三边关系定理，　　所以　于是得　故图象应是去掉端点的一条线段。
正解：有题意可得　（）
　　　当时　所以A（5，10）　
　当时　所以B（10，0）
　　　所以所求函数（）的图象，如图2所示　　 　　　　　　　　　　　　　　　　　图2
练习：1、已知函数是一次函数，则m=＿＿＿。
2、已知一次函数的图象经过点A（0，3）且与两坐标轴所围成的三角形的面积是3，则这个一次函数的表达式为＿＿＿。
3、已知一次函数　当时对应的y的值为，则k的值为＿＿＿。
4、已知直线不经过第四象限，则的取值范围是＿＿＿。
5、如图，在ABC中，，AC＝6,　BC=8　设P为BC上任意一点，点P与B，C不重合，且CP＝x，　若　　
求y与x的函数关系。
求自变量x的取值范围。　　　　　　　　　　　　图3
画出函数的图象。
答案：1、－1　　2、　或　　3、　　　4、
5、（1） （2） （3）图象如图4
　　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　图4
A、
O
x
4
y
20
B、
O
x
4
y
20
C、
O
x
4
y
20
D、
O
x
4
y
20