人教版数学八年级上册11.3.1多边形课件(22张ppt)
文档属性
| 名称 | 人教版数学八年级上册11.3.1多边形课件(22张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 564.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-18 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
11.3
多边形及其内角和
11.3.1
多边形
新课导入
你能从图中想象出几个由一些线段围成的图形吗?
学习目标:
1.能叙述多边形、多边形的内角、外角和对角线的意义.
2.知道什么是凸多边形和正多边形.
学习重、难点:
重点:多边形及其有关的概念.
难点:三角形外角性质的证明.
推进新课
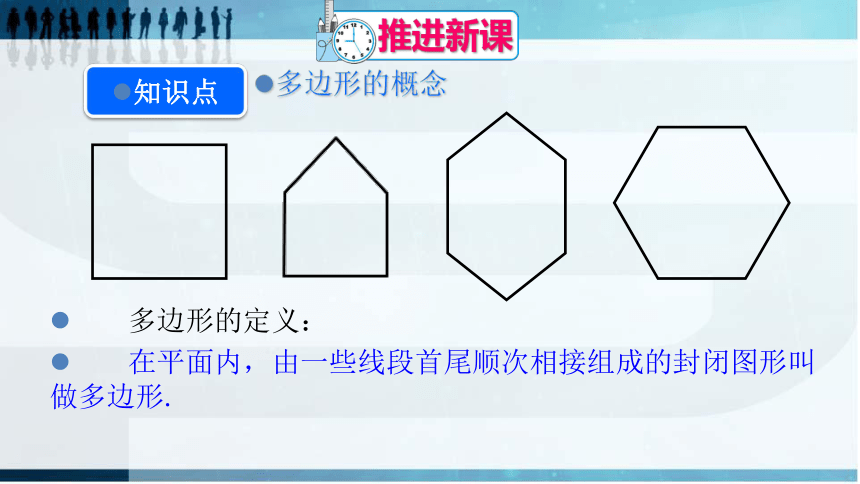
多边形的概念
知识点
多边形的定义:
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
如果一个多边形由
n
条线段组成,那么这个多边形就叫做
n
边形.
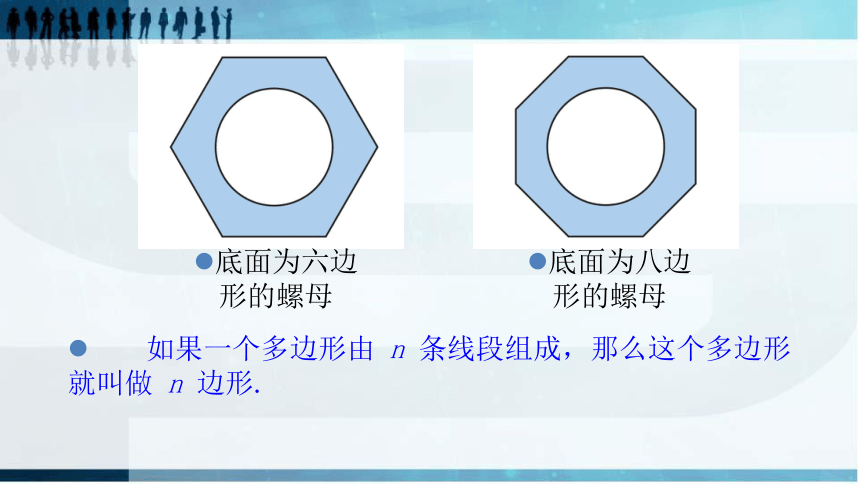
底面为六边形的螺母
底面为八边形的螺母
A
B
C
D
E
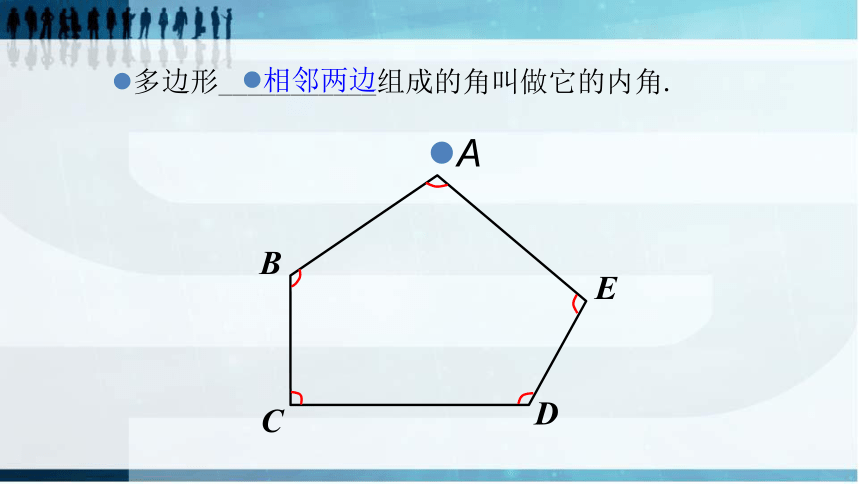
多边形___________组成的角叫做它的内角.
相邻两边
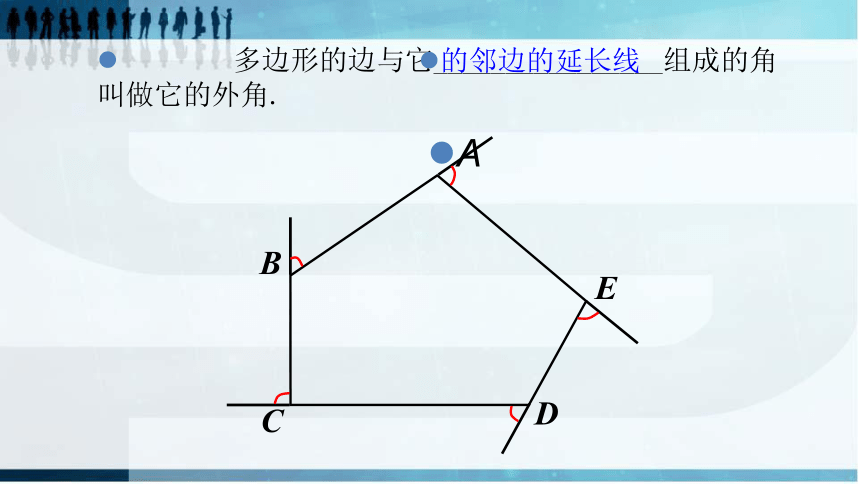
多边形的边与它________________组成的角叫做它的外角.
的邻边的延长线
A
B
C
D
E
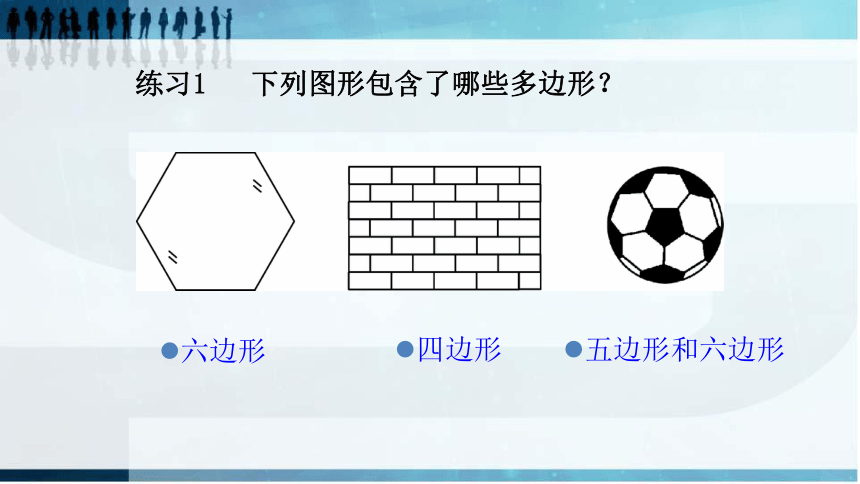
练习1
下列图形包含了哪些多边形?
六边形
四边形
五边形和六边形
A
B
C
D
E
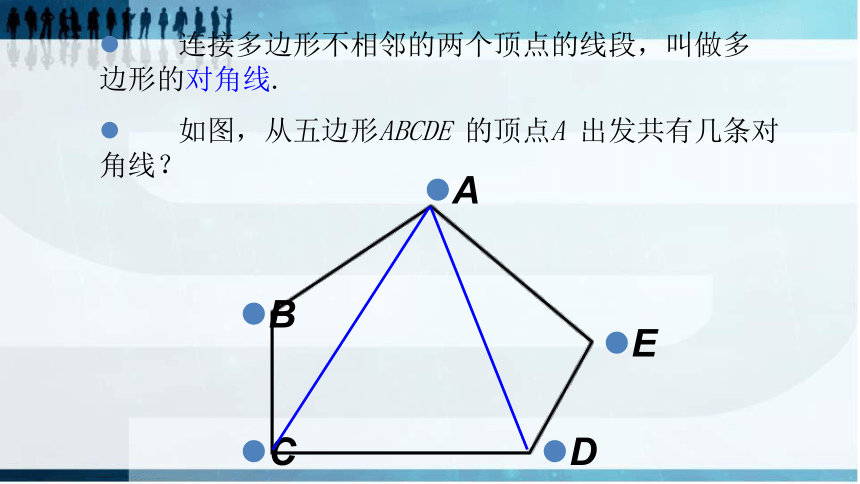
连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
如图,从五边形ABCDE
的顶点A
出发共有几条对角线?
凸四边形
观察 你能说出这两个图形的异同点吗?
A
B
C
D
B
D
C
A
想一想 正方形的边、角有什么特点?
各个角都相等,各条边都相等的多边形叫做正多边形.
正三角形
正方形
正五边形
正六边形
从四边形、五边形、六边形中探究
n
边形的对角线条数
m
与边数
n
之间的关系.
形状
图形
从多边形的一个顶点引出的对角线条数
三角形
四边形
五边形
六边形
……
n
边形
······
0
3
-
3
=
4
-
3
=
5
-
3
=
6
-
3
=
n
-
3
1
2
3
······
n
边形的对角线条数
m
与边数
n
之间的关系.
练习2
画出下图多边形的全部对角线.
练习3
四边形的一条对角线将四边形分成几个三角形?从五边形的一个顶点出发,可以画出几条对角线?它们将五边形分成了几个三角形?
2个三角形
2条对角线
3个三角形
随堂演练
1.六边形的对角线共有(
)
A.6条
B.7条
C.8条
D.9条
2.下列属于正多边形的是(
)
A.长方形
B.等边三角形
C.梯形
D.圆
D
B
基础巩固
3.从一个顶点出发的对角线,可以把十边形分成互不重叠的三角形的个数(
)
A.7个
B.8个
C.9个
D.10个
4.十二边形共有_____条对角线,过一个顶点可作_____条对角线,可把十二边形分成_____个三角形.
B
54
9
10
5.某学校七年级六个班举行篮球比赛,比赛采用单循环积分制(即每个班都进行一次比赛).一共需要多少场比赛?
解:一共需要15场比赛.如图:
综合应用
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
凸四边形
A
B
C
D
B
D
C
A
正三角形
正方形
正五边形
正六边形
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
000000000000
学习本课时,可让学生先自主探索再合作交流,小组内、小组之间充分交流后概括所得结论,既巩固了三角形的知识,又用类比的方法引出多边形的有关概念,加深对本课时的学习.
教学反思
11.3
多边形及其内角和
11.3.1
多边形
新课导入
你能从图中想象出几个由一些线段围成的图形吗?
学习目标:
1.能叙述多边形、多边形的内角、外角和对角线的意义.
2.知道什么是凸多边形和正多边形.
学习重、难点:
重点:多边形及其有关的概念.
难点:三角形外角性质的证明.
推进新课
多边形的概念
知识点
多边形的定义:
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
如果一个多边形由
n
条线段组成,那么这个多边形就叫做
n
边形.
底面为六边形的螺母
底面为八边形的螺母
A
B
C
D
E
多边形___________组成的角叫做它的内角.
相邻两边
多边形的边与它________________组成的角叫做它的外角.
的邻边的延长线
A
B
C
D
E
练习1
下列图形包含了哪些多边形?
六边形
四边形
五边形和六边形
A
B
C
D
E
连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
如图,从五边形ABCDE
的顶点A
出发共有几条对角线?
凸四边形
观察 你能说出这两个图形的异同点吗?
A
B
C
D
B
D
C
A
想一想 正方形的边、角有什么特点?
各个角都相等,各条边都相等的多边形叫做正多边形.
正三角形
正方形
正五边形
正六边形
从四边形、五边形、六边形中探究
n
边形的对角线条数
m
与边数
n
之间的关系.
形状
图形
从多边形的一个顶点引出的对角线条数
三角形
四边形
五边形
六边形
……
n
边形
······
0
3
-
3
=
4
-
3
=
5
-
3
=
6
-
3
=
n
-
3
1
2
3
······
n
边形的对角线条数
m
与边数
n
之间的关系.
练习2
画出下图多边形的全部对角线.
练习3
四边形的一条对角线将四边形分成几个三角形?从五边形的一个顶点出发,可以画出几条对角线?它们将五边形分成了几个三角形?
2个三角形
2条对角线
3个三角形
随堂演练
1.六边形的对角线共有(
)
A.6条
B.7条
C.8条
D.9条
2.下列属于正多边形的是(
)
A.长方形
B.等边三角形
C.梯形
D.圆
D
B
基础巩固
3.从一个顶点出发的对角线,可以把十边形分成互不重叠的三角形的个数(
)
A.7个
B.8个
C.9个
D.10个
4.十二边形共有_____条对角线,过一个顶点可作_____条对角线,可把十二边形分成_____个三角形.
B
54
9
10
5.某学校七年级六个班举行篮球比赛,比赛采用单循环积分制(即每个班都进行一次比赛).一共需要多少场比赛?
解:一共需要15场比赛.如图:
综合应用
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
凸四边形
A
B
C
D
B
D
C
A
正三角形
正方形
正五边形
正六边形
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
000000000000
学习本课时,可让学生先自主探索再合作交流,小组内、小组之间充分交流后概括所得结论,既巩固了三角形的知识,又用类比的方法引出多边形的有关概念,加深对本课时的学习.
教学反思
