人教版八年级数学上册第十一章三角形章末复习课件(37张ppt)
文档属性
| 名称 | 人教版八年级数学上册第十一章三角形章末复习课件(37张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 444.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-18 00:00:00 | ||
图片预览









文档简介
(共37张PPT)
章末复习
复习导入
虽说我们从小学开始,就零零散散地学习了一些三角形的知识,但系统地学习三角形的知识,是从本章开始的,下面我们再一起回顾一下本章的知识要点和几何研究方法.
复习目标:
1.梳理三角形和多边形有关的知识点.
2.了解三角形与多边形的内在联系.
复习重、难点:
重点:与三角形和多边形相关的概念.
难点:与三角形和多边形有关的计算.
知识巩固
问题1
请同学们回答下列问题:
(1)三角形的三边之间有怎样的关系?得出这个结论的依据是什么?
(2)三角形的三个内角之间有怎样的关系?如何证明这个结论?
梳理知识
问题1
请同学们回答下列问题:
(3)直角三角形的两个锐角之间有怎样的关系?三角形的一个外角和它不相邻的两个内角之间有怎样的关系?这些结论能由三角形内角和定理得出吗?
(4)n
边形的n
个内角有怎样的关系?如何推出这个结论?
(5)n
边形的外角大小和与n
有关吗?为什么?
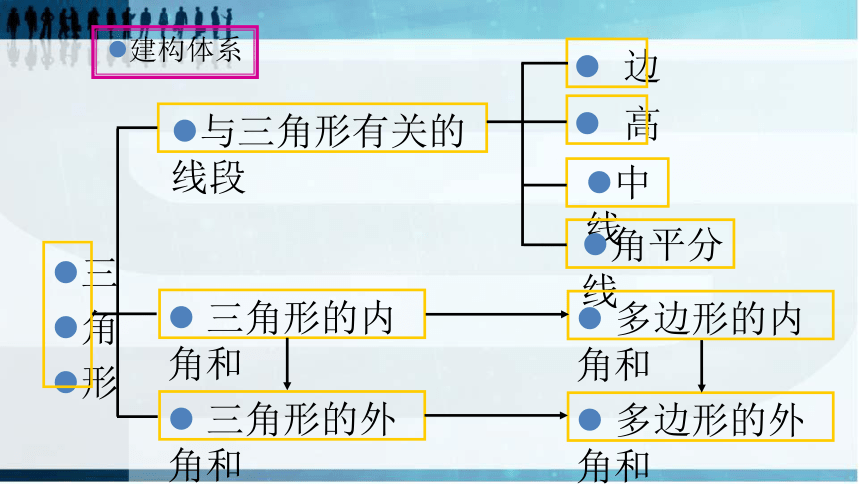
建构体系
边
高
中线
角平分线
多边形的内角和
多边形的外角和
与三角形有关的线段
三
角
形
三角形的内角和
三角形的外角和
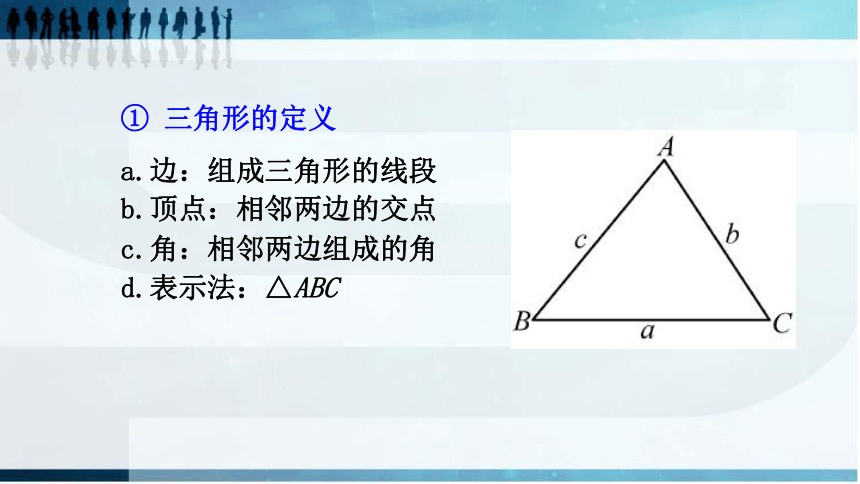
①
三角形的定义
a.边:组成三角形的线段
b.顶点:相邻两边的交点
c.角:相邻两边组成的角
d.表示法:△ABC
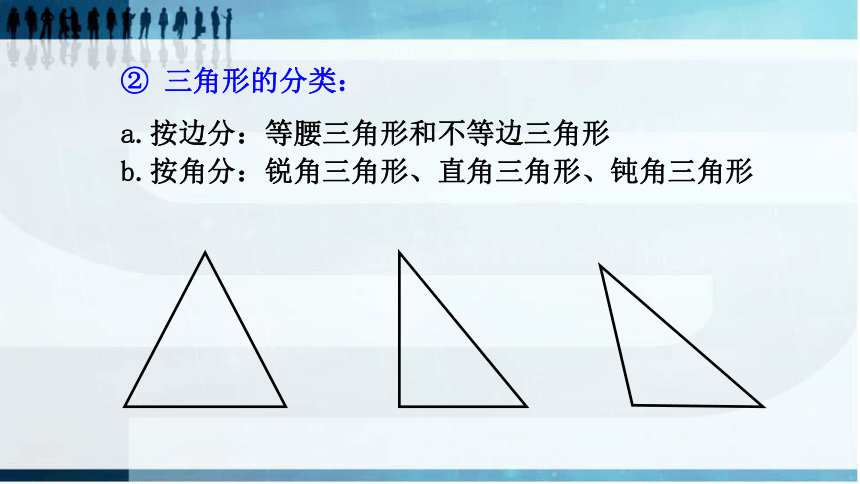
②
三角形的分类:
a.按边分:等腰三角形和不等边三角形
b.按角分:锐角三角形、直角三角形、钝角三角形
③
三角形的主要线段:
a.三角形的中线:连接三角形的一个顶点和它对边中点的线段叫做三角形的中线.
b.三角形的角平分线:三角形一个内角的平分线与它的对边相交,这个角的顶点与对边上的交点之间的线段,叫做三角形的角平分线.
c.三角形的高:从三角形的一个顶点向它的对边作垂线,所得线段叫做三角形的高.
④三角形三边间的关系:
三角形两边的和大于第三边.
⑤三角形的稳定性及应用:
三角形具有稳定性.
⑥多边形的对角线、内角和、外角和:
n
边形的对角线条数等于
,内角和等于(n-2)·180°,外角和等于360°.
课堂练习
A
组 复习与三角形有关的线段:
1.若三角形的两边分别为
3
和
5
,则第三边长m
的取值范围是__________.
2
<
m
<
8
A
组 复习与三角形有关的线段:
2.如图:
(1)若AD
⊥BC,垂足
为D,则:
∠_____
=∠_____
=
90°;
ADB
ADC
A
B
C
D
E
F
A
组 复习与三角形有关的线段:
2.如图:
(2)若∠BAE
=∠CAE,
AE
与BC
相交于点
E,则:
线段AE
是△ABC
的_________;
A
B
C
D
E
F
角平分线
A
B
C
D
E
F
BF
A
组 复习与三角形有关的线段:
2.如图:
(3)若AF
=CF,BF
与
AC
相交于点F,
则:△ABC
的中
线是
.
B
组 巩固与三角形有关的角:
如图,在△ABC
中,∠BAC
=80°,∠ABC
=60°.
(1)∠C
= ;
(2)若AE
是△ABC
的
角平分线,则:
∠AEC
=
;
(3)若BF
是△ABC
的
高,与角平分线
AE
相交于点O,则∠EOF
=
.
40°
100°
130°
A
B
C
O
E
F
例1
已知等腰三角形的两边长分别为10
和6
,则三角形的周长是 .
变式1
若等腰三角形的周长为20,一边长为4,则其他两边长为 .
22或26
8和8
典型例题
变式2 小明用一条长20
cm的细绳围成了一个等腰三角形,他想使这个三角形的一边长是另一边长的2倍,那么这个三角形的各边的长分别是多少?
解:设较短的边长为
x
cm,则较长的边长为2x
cm.
若较短的边为腰,则x
+
x
+
2x
=20.
解得 x
=5.
即 2x
=10.
因为
5
+
5
=10,不符合三角形两边的和大于第
三边,所以不能围成腰长5
cm的等腰三角形.
解:若较长的边为腰,则
x
+
2x
+
2x
=20.
解得 x
=
4.
所以,这个三角形的三边分别为:
4
cm,
8
cm,
8
cm.
变式2 小明用一条长20
cm的细绳围成了一个等腰三角形,他想使这个三角形的一边长是另一边长的2倍,那么这个三角形的各边的长分别是多少?
例2 如图,在△ABC
中,∠
ABC
,∠
ACB
的平分线BD,CE
交于点O.
若∠ABC
=40°,∠ACB
=60°,则:
∠BOC
=
.
A
B
C
O
E
D
130°
例2 如图,在△ABC
中,∠
ABC
,∠
ACB
的平分线BD,CE
交于点O.
变式1 若∠A
=80°,则∠BOC
=
.
变式2 你能猜想出∠BOC
与∠A
之间的数量关系吗?
A
B
C
O
E
D
∠BOC
=
90°+
∠A
130°
A
B
C
O
E
D
变式3 如图,若换成两
外角平分线相交于O,则
∠BOC
与∠A
又有怎样的数
量关系?
∠BOC
=
90°-
∠A
变式4 如图,若换成一内角与一外角平分线相交于点O,则∠BOC与∠A
又有怎样的数量关系?
∠BOC
=
∠A
A
B
C
O
E
D
变式5 如图,若换成两条高相交于点O,
∠A
与∠BOC
又有怎样的数量关系?
∠BOC
=
180°-∠A
A
B
C
O
E
D
练习1(1)三角形的两边分别为3和5,则三角形周长y
的范围是(
)
A.2<y<8
B.10<y<18
C.10<y<16
D.无法确定
C
练习1(2)在下列条件中:①
∠A
+
∠B
=∠C,②∠A:∠B:∠C
=1:2:3,③∠A
=
90°-∠B,④∠A
=∠B
=∠C中,能确定△ABC是直角三角形的条件有(
)
A.1个
B.2个
C.3个
D.4个
C
练习1(3)已知一个多边形的内角和是外角和的2倍,则这个多边形的边数为______.
6
练习2
已知三角形的两个外角分别为a°,b°,且满足(a-50)2
=-|a+b-200|,求此三角形各角的度数.
解:∵(a-50)2+|a+b-200|=0,
∴其中两内角为130°,30°,另一个内角为20°.
练习3
三角形的最长边为10,另两边的长分别为x和4,周长为c,求x
和c
的取值范围.
解:根据三角形两边之和大于第三边、两边之差小于第三边.又最长边为10,得x
的取值范围.
10-4<x<10
∴6<x<10.
又c
=
10+4+x
=
x+14,∴20<c<24.
1.已知a、b、c是三角形的三边长,化简:|a-b+c|-|a-b-c|=_________.
2a-2b
随堂演练
基础巩固
2.如图,在直角三角形ABC中,∠ACB
=90°,CD是AB边上的高,AB
=
13cm,BC
=
12cm,AC
=
5cm.
综合应用
(1)求出△ABC的面积及
CD的长;
(2)已知BE是
△ABC的边AC上的中线,求出△ABE的面积.
解:
3.一轮船由B
处向C处航行,在B
处测得C处在B
的北偏东75°方向上,在海岛上的观察所A
测得B
在A
的南偏西30°方向,C
在A的南偏东25°方向;若轮船行使到C
处,那么从C
处看A、B
两处的视角∠ACB是多少度?
拓展延伸
解:根据题意,画出示意图如图所示:
另求出∠ABC
=75°-
30°=
45°,∠BAC
=
30°+25°=
55°,
所以∠ACB
=180°-
45°-
55°=
80°.
课堂小结
边
高
中线
角平分线
多边形的内角和
多边形的外角和
与三角形有关的线段
三
角
形
三角形的内角和
三角形的外角和
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
利用知识回顾与典例剖析,使学生进一步巩固和深化对所学知识的理解,建立起清晰的知识框架,形成严谨的思维习惯.
教学反思
章末复习
复习导入
虽说我们从小学开始,就零零散散地学习了一些三角形的知识,但系统地学习三角形的知识,是从本章开始的,下面我们再一起回顾一下本章的知识要点和几何研究方法.
复习目标:
1.梳理三角形和多边形有关的知识点.
2.了解三角形与多边形的内在联系.
复习重、难点:
重点:与三角形和多边形相关的概念.
难点:与三角形和多边形有关的计算.
知识巩固
问题1
请同学们回答下列问题:
(1)三角形的三边之间有怎样的关系?得出这个结论的依据是什么?
(2)三角形的三个内角之间有怎样的关系?如何证明这个结论?
梳理知识
问题1
请同学们回答下列问题:
(3)直角三角形的两个锐角之间有怎样的关系?三角形的一个外角和它不相邻的两个内角之间有怎样的关系?这些结论能由三角形内角和定理得出吗?
(4)n
边形的n
个内角有怎样的关系?如何推出这个结论?
(5)n
边形的外角大小和与n
有关吗?为什么?
建构体系
边
高
中线
角平分线
多边形的内角和
多边形的外角和
与三角形有关的线段
三
角
形
三角形的内角和
三角形的外角和
①
三角形的定义
a.边:组成三角形的线段
b.顶点:相邻两边的交点
c.角:相邻两边组成的角
d.表示法:△ABC
②
三角形的分类:
a.按边分:等腰三角形和不等边三角形
b.按角分:锐角三角形、直角三角形、钝角三角形
③
三角形的主要线段:
a.三角形的中线:连接三角形的一个顶点和它对边中点的线段叫做三角形的中线.
b.三角形的角平分线:三角形一个内角的平分线与它的对边相交,这个角的顶点与对边上的交点之间的线段,叫做三角形的角平分线.
c.三角形的高:从三角形的一个顶点向它的对边作垂线,所得线段叫做三角形的高.
④三角形三边间的关系:
三角形两边的和大于第三边.
⑤三角形的稳定性及应用:
三角形具有稳定性.
⑥多边形的对角线、内角和、外角和:
n
边形的对角线条数等于
,内角和等于(n-2)·180°,外角和等于360°.
课堂练习
A
组 复习与三角形有关的线段:
1.若三角形的两边分别为
3
和
5
,则第三边长m
的取值范围是__________.
2
<
m
<
8
A
组 复习与三角形有关的线段:
2.如图:
(1)若AD
⊥BC,垂足
为D,则:
∠_____
=∠_____
=
90°;
ADB
ADC
A
B
C
D
E
F
A
组 复习与三角形有关的线段:
2.如图:
(2)若∠BAE
=∠CAE,
AE
与BC
相交于点
E,则:
线段AE
是△ABC
的_________;
A
B
C
D
E
F
角平分线
A
B
C
D
E
F
BF
A
组 复习与三角形有关的线段:
2.如图:
(3)若AF
=CF,BF
与
AC
相交于点F,
则:△ABC
的中
线是
.
B
组 巩固与三角形有关的角:
如图,在△ABC
中,∠BAC
=80°,∠ABC
=60°.
(1)∠C
= ;
(2)若AE
是△ABC
的
角平分线,则:
∠AEC
=
;
(3)若BF
是△ABC
的
高,与角平分线
AE
相交于点O,则∠EOF
=
.
40°
100°
130°
A
B
C
O
E
F
例1
已知等腰三角形的两边长分别为10
和6
,则三角形的周长是 .
变式1
若等腰三角形的周长为20,一边长为4,则其他两边长为 .
22或26
8和8
典型例题
变式2 小明用一条长20
cm的细绳围成了一个等腰三角形,他想使这个三角形的一边长是另一边长的2倍,那么这个三角形的各边的长分别是多少?
解:设较短的边长为
x
cm,则较长的边长为2x
cm.
若较短的边为腰,则x
+
x
+
2x
=20.
解得 x
=5.
即 2x
=10.
因为
5
+
5
=10,不符合三角形两边的和大于第
三边,所以不能围成腰长5
cm的等腰三角形.
解:若较长的边为腰,则
x
+
2x
+
2x
=20.
解得 x
=
4.
所以,这个三角形的三边分别为:
4
cm,
8
cm,
8
cm.
变式2 小明用一条长20
cm的细绳围成了一个等腰三角形,他想使这个三角形的一边长是另一边长的2倍,那么这个三角形的各边的长分别是多少?
例2 如图,在△ABC
中,∠
ABC
,∠
ACB
的平分线BD,CE
交于点O.
若∠ABC
=40°,∠ACB
=60°,则:
∠BOC
=
.
A
B
C
O
E
D
130°
例2 如图,在△ABC
中,∠
ABC
,∠
ACB
的平分线BD,CE
交于点O.
变式1 若∠A
=80°,则∠BOC
=
.
变式2 你能猜想出∠BOC
与∠A
之间的数量关系吗?
A
B
C
O
E
D
∠BOC
=
90°+
∠A
130°
A
B
C
O
E
D
变式3 如图,若换成两
外角平分线相交于O,则
∠BOC
与∠A
又有怎样的数
量关系?
∠BOC
=
90°-
∠A
变式4 如图,若换成一内角与一外角平分线相交于点O,则∠BOC与∠A
又有怎样的数量关系?
∠BOC
=
∠A
A
B
C
O
E
D
变式5 如图,若换成两条高相交于点O,
∠A
与∠BOC
又有怎样的数量关系?
∠BOC
=
180°-∠A
A
B
C
O
E
D
练习1(1)三角形的两边分别为3和5,则三角形周长y
的范围是(
)
A.2<y<8
B.10<y<18
C.10<y<16
D.无法确定
C
练习1(2)在下列条件中:①
∠A
+
∠B
=∠C,②∠A:∠B:∠C
=1:2:3,③∠A
=
90°-∠B,④∠A
=∠B
=∠C中,能确定△ABC是直角三角形的条件有(
)
A.1个
B.2个
C.3个
D.4个
C
练习1(3)已知一个多边形的内角和是外角和的2倍,则这个多边形的边数为______.
6
练习2
已知三角形的两个外角分别为a°,b°,且满足(a-50)2
=-|a+b-200|,求此三角形各角的度数.
解:∵(a-50)2+|a+b-200|=0,
∴其中两内角为130°,30°,另一个内角为20°.
练习3
三角形的最长边为10,另两边的长分别为x和4,周长为c,求x
和c
的取值范围.
解:根据三角形两边之和大于第三边、两边之差小于第三边.又最长边为10,得x
的取值范围.
10-4<x<10
∴6<x<10.
又c
=
10+4+x
=
x+14,∴20<c<24.
1.已知a、b、c是三角形的三边长,化简:|a-b+c|-|a-b-c|=_________.
2a-2b
随堂演练
基础巩固
2.如图,在直角三角形ABC中,∠ACB
=90°,CD是AB边上的高,AB
=
13cm,BC
=
12cm,AC
=
5cm.
综合应用
(1)求出△ABC的面积及
CD的长;
(2)已知BE是
△ABC的边AC上的中线,求出△ABE的面积.
解:
3.一轮船由B
处向C处航行,在B
处测得C处在B
的北偏东75°方向上,在海岛上的观察所A
测得B
在A
的南偏西30°方向,C
在A的南偏东25°方向;若轮船行使到C
处,那么从C
处看A、B
两处的视角∠ACB是多少度?
拓展延伸
解:根据题意,画出示意图如图所示:
另求出∠ABC
=75°-
30°=
45°,∠BAC
=
30°+25°=
55°,
所以∠ACB
=180°-
45°-
55°=
80°.
课堂小结
边
高
中线
角平分线
多边形的内角和
多边形的外角和
与三角形有关的线段
三
角
形
三角形的内角和
三角形的外角和
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
利用知识回顾与典例剖析,使学生进一步巩固和深化对所学知识的理解,建立起清晰的知识框架,形成严谨的思维习惯.
教学反思
