人教版八年级上册 第十一章 三角形 11.1 与三角形有关的线段 11.1.2 三角形的高、中线与角平分线 上课课件(27张PPT)
文档属性
| 名称 | 人教版八年级上册 第十一章 三角形 11.1 与三角形有关的线段 11.1.2 三角形的高、中线与角平分线 上课课件(27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 942.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-19 00:00:00 | ||
图片预览




文档简介
(共27张PPT)
11.1.2
三角形的高、中线与角平分线
11.1.3
三角形的稳定性
你还记得“过一点画已知
直线的垂线”吗?
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
1.掌握三角形中三条重要的线段的概念;
2.了解三角形的稳定性在日常生活中的应用.
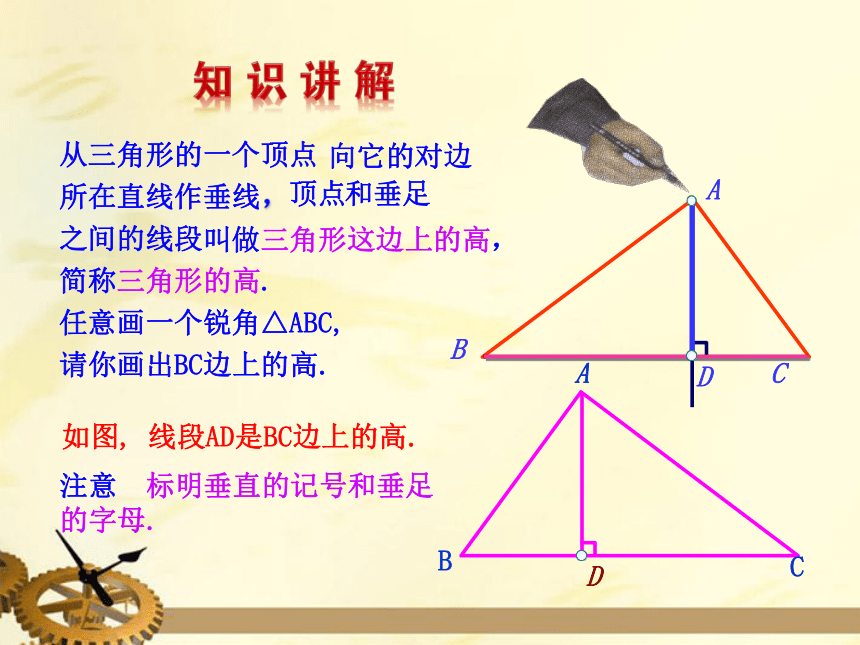
从三角形的一个顶点
向它的对边
所在直线作垂线,
顶点
和垂足
之间的线段
叫做三角形这边上的高,
简称三角形的高.
如图,
线段AD是BC边上的高.
任意画一个锐角△ABC,
A
B
C
请你画出BC边上的高.
注意
标明垂直的记号和垂足的字母.
D
A
B
C
D
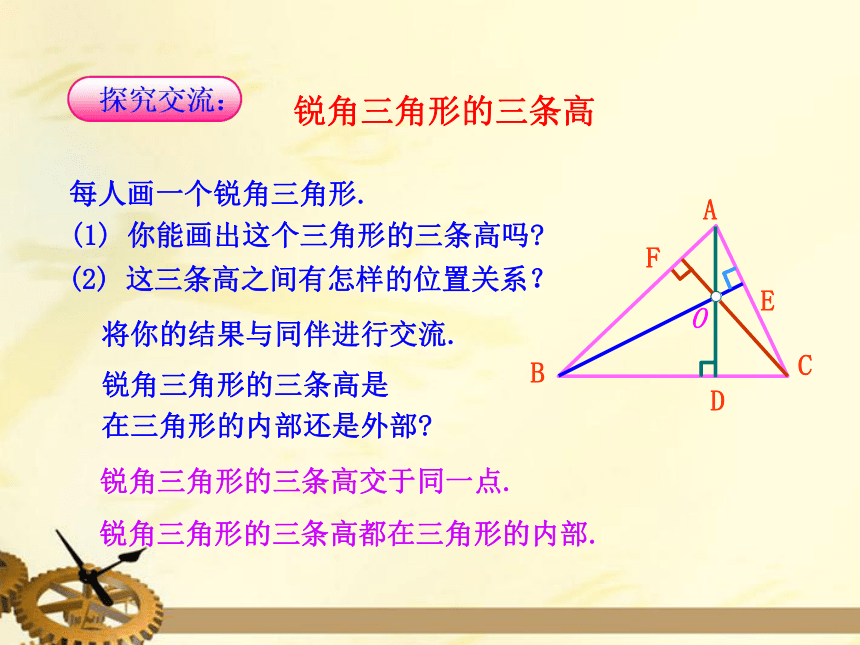
锐角三角形的三条高
每人画一个锐角三角形.
(1)
你能画出这个三角形的三条高吗?
(2)
这三条高之间有怎样的位置关系?
将你的结果与同伴进行交流.
O
锐角三角形的三条高是
在三角形的内部还是外部?
A
B
C
D
E
F
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部.
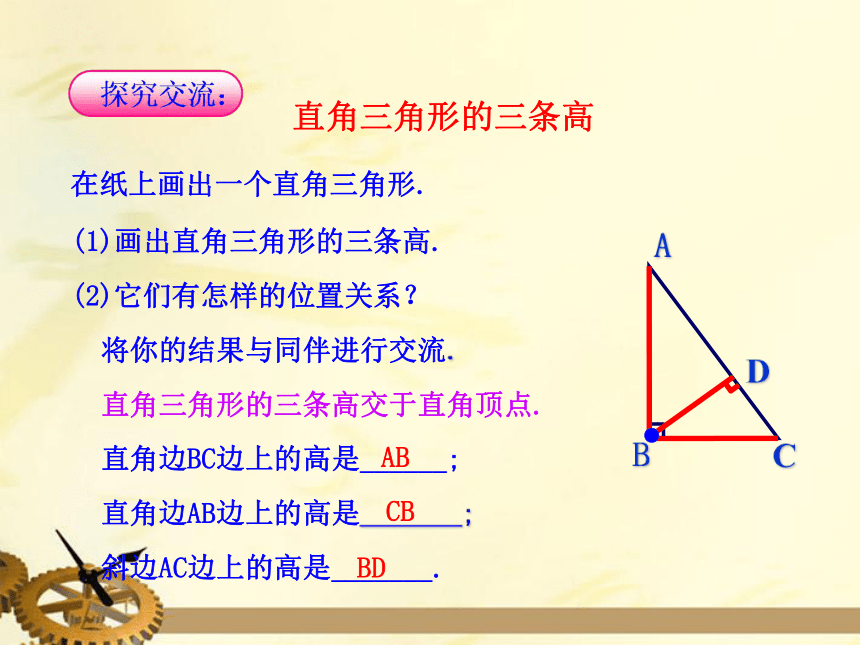
直角三角形的三条高
在纸上画出一个直角三角形.
将你的结果与同伴进行交流.
A
B
C
(1)画出直角三角形的三条高.
直角边BC边上的高是______;
AB
直角边AB边上的高是
;
CB
(2)它们有怎样的位置关系?
D
斜边AC边上的高是_______.
BD
●
直角三角形的三条高交于直角顶点.
A
B
C
D
E
F
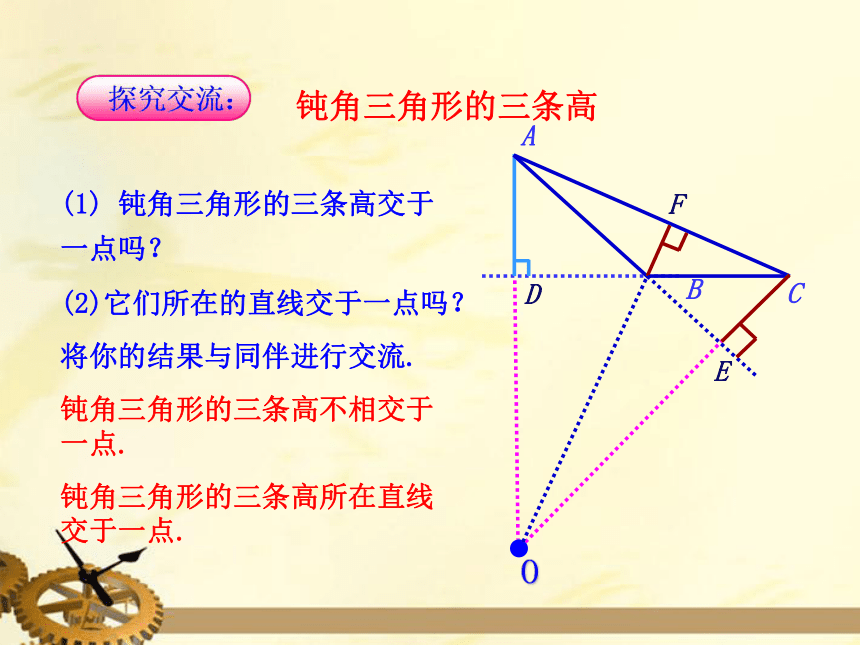
钝角三角形的三条高
(1)
钝角三角形的三条高交于
一点吗?
(2)它们所在的直线交于一点吗?
将你的结果与同伴进行交流.
O
钝角三角形的三条高不相交于一点.
钝角三角形的三条高所在直线交于一点.
从三角形的一个顶点向它的对边所在直线作垂线,
顶点和垂足之间的线段
叫做三角形这边上的高.
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三条高所在直线的交点的位置
三角形
内部
直角顶点
三角形
外部
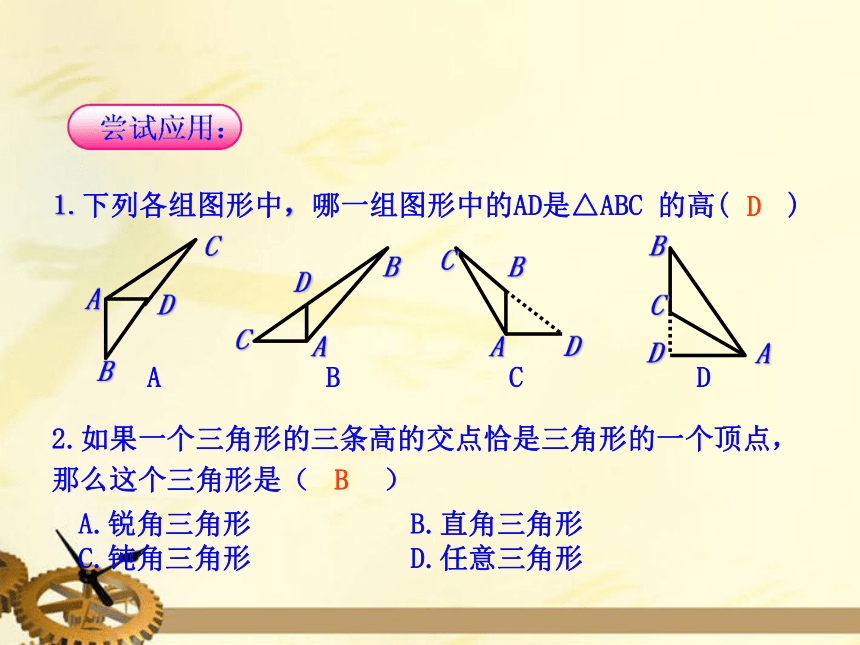
2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.任意三角形
1.下列各组图形中,哪一组图形中的AD是△ABC
的高(
)
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
B
D
三角形的中线
在三角形中,连接一个
顶点与它对边中点的线段,
叫做这个三角形这边上的中线.
A
B
C
D
因为AD是△ABC的中线,
任意画一个三角形,然后利用刻度尺画出这个三角形三条边上的中线,你发现了什么?
●
●
E
F
O
三角形的三条中线相交于一点,交点在三角形的内部.
三角形三条中线的交点叫做三角形的重心.
所以BD=CD=
BC.
叫做三角形的角平分线.
A
B
C
D
因为AD是△ABC的角平分线,
任意画一个三角形,然后利用量角器画出这个三角形三个角的角平分线,你发现了什么?
●
●
在三角形中,一个
内角的角平分线与它的对边相交,
这个角的顶点与交点之间的线段,
︶
︶
1
2
三角形的三条角平分线相交于一点,交点在三角形的内部.
所以∠BAD
=∠CAD
=
∠BAC.
A
C
B
F
E
D
O
因为BE是△ABC的角平分线,
所以______=________=
_____.
所以∠ACB=2____
=2_____.
∠ABE
∠CBE
∠ABC
∠ACF
因为CF是△ABC的角平分线,
∠BCF
三角形的角平分线与角的平分线有什么区别?
三角形的角平分线是一条线段,角的平分线是一条射线.
2
2
BD
6
cm?
练习1.如图,AD,BE,CF
是△ABC
的三条中线.
(1)AC
=
AE
=
EC;
CD
=
;
AF
=
AB;
(2)若S△ABC
=
12
cm2,
则S△ABD
=
.
A
B
C
D
E
F
G
∠2
2.如图,AD,BE,CF
是△ABC
的三条角平分线,则:
∠1
=
;
∠3
=
;
∠ACB
=
2
.
∠ABC
∠4
A
B
C
D
E
F
1
2
3
4
三角形的稳定性
三角形具有稳定性,
四边形没有稳定性.
盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,为什么要这样做呢?
三角形的稳定性
将四边形木架上再钉一根木条,将它的一对顶点连接起来,然后再扭动它,这时木架的形状会改变吗?为什么?
不会改变.钉上的木条将四边形分成两个三角形,而三角形具有稳定性.
斜梁
斜梁
直
梁
三角形的稳定性
如图,工人师傅砌门时,常用木条EF,EG固定门框ABCD,使其不变形,这种做法根据的是三角形的稳定性.
C
E
B
A
F
D
G
三角形的稳定性
四边形不稳定性的应用
活动挂架
1.下列图形中具有稳定性的是(
)
A.正方形
B.长方形
C.直角三角形
D.平行四边形
C
2.要使下列木架稳定各至少需要多少根木棍?
答案:1
2
3
3.你能举例说明三角形的稳定性在实际生活
中的应用吗?
三角形的稳定性的应用举例:
(1)自行车的几个梁形成三角支撑;
(2)钢架桥的钢架做成三角形;
(3)起重机的力臂做成三角形;
(4)照相机的支架做成三角形;
(5)高压电线杆的支架做成三角形.
1.三角形的三条重要线段:高、中线、角平分线.
2.三角形的稳定性.
通过本课时的学习,需要我们掌握:
【解析】选A.四边形没有稳定性.
1.下列设备,没有利用三角形的稳定性的是(
)
A.活动的四边形衣架
B.起重机
C.屋顶三角形钢架
D.索道支架
2.(连云港·中考)小华在电话中问小明:“已知一个三角形三边长分别是4,9,12,如何求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是(
)
【解析】选C.A,D项作的不是三角形的高,B项作的是三角形的高,但不是最长边上的高.
3.如图,在ΔABC中,AE是中线,
AD是角平分线,AF是高.填空:
(1)BE=
=
;
(2)∠BAD=
=
;
(3)∠AFB=
=90°;
(4)SΔABC=
.
CE
BC
∠CAD
∠BAC
∠AFC
BC?AF
4.如图,在△ABC中,
∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,CF⊥AD于H,判断下列说法哪些是正确的,哪些是错误的.
⌒
⌒
A
B
C
D
E
1
2
F
G
H
①AD是△ABE的角平分线(
)
②BE是△
ABD边AD上的中线(
)
③BE是△
ABC边AC上的中线(
)
④CH是△
ACD边AD上的高(
)
三角形的高、中线与角平分线都是线段.
×
×
×
√
理想是指路明星。没有理想,就没有坚定的方向,而没有方向,
就没有生活.
11.1.2
三角形的高、中线与角平分线
11.1.3
三角形的稳定性
你还记得“过一点画已知
直线的垂线”吗?
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
1.掌握三角形中三条重要的线段的概念;
2.了解三角形的稳定性在日常生活中的应用.
从三角形的一个顶点
向它的对边
所在直线作垂线,
顶点
和垂足
之间的线段
叫做三角形这边上的高,
简称三角形的高.
如图,
线段AD是BC边上的高.
任意画一个锐角△ABC,
A
B
C
请你画出BC边上的高.
注意
标明垂直的记号和垂足的字母.
D
A
B
C
D
锐角三角形的三条高
每人画一个锐角三角形.
(1)
你能画出这个三角形的三条高吗?
(2)
这三条高之间有怎样的位置关系?
将你的结果与同伴进行交流.
O
锐角三角形的三条高是
在三角形的内部还是外部?
A
B
C
D
E
F
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部.
直角三角形的三条高
在纸上画出一个直角三角形.
将你的结果与同伴进行交流.
A
B
C
(1)画出直角三角形的三条高.
直角边BC边上的高是______;
AB
直角边AB边上的高是
;
CB
(2)它们有怎样的位置关系?
D
斜边AC边上的高是_______.
BD
●
直角三角形的三条高交于直角顶点.
A
B
C
D
E
F
钝角三角形的三条高
(1)
钝角三角形的三条高交于
一点吗?
(2)它们所在的直线交于一点吗?
将你的结果与同伴进行交流.
O
钝角三角形的三条高不相交于一点.
钝角三角形的三条高所在直线交于一点.
从三角形的一个顶点向它的对边所在直线作垂线,
顶点和垂足之间的线段
叫做三角形这边上的高.
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三条高所在直线的交点的位置
三角形
内部
直角顶点
三角形
外部
2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.任意三角形
1.下列各组图形中,哪一组图形中的AD是△ABC
的高(
)
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
B
D
三角形的中线
在三角形中,连接一个
顶点与它对边中点的线段,
叫做这个三角形这边上的中线.
A
B
C
D
因为AD是△ABC的中线,
任意画一个三角形,然后利用刻度尺画出这个三角形三条边上的中线,你发现了什么?
●
●
E
F
O
三角形的三条中线相交于一点,交点在三角形的内部.
三角形三条中线的交点叫做三角形的重心.
所以BD=CD=
BC.
叫做三角形的角平分线.
A
B
C
D
因为AD是△ABC的角平分线,
任意画一个三角形,然后利用量角器画出这个三角形三个角的角平分线,你发现了什么?
●
●
在三角形中,一个
内角的角平分线与它的对边相交,
这个角的顶点与交点之间的线段,
︶
︶
1
2
三角形的三条角平分线相交于一点,交点在三角形的内部.
所以∠BAD
=∠CAD
=
∠BAC.
A
C
B
F
E
D
O
因为BE是△ABC的角平分线,
所以______=________=
_____.
所以∠ACB=2____
=2_____.
∠ABE
∠CBE
∠ABC
∠ACF
因为CF是△ABC的角平分线,
∠BCF
三角形的角平分线与角的平分线有什么区别?
三角形的角平分线是一条线段,角的平分线是一条射线.
2
2
BD
6
cm?
练习1.如图,AD,BE,CF
是△ABC
的三条中线.
(1)AC
=
AE
=
EC;
CD
=
;
AF
=
AB;
(2)若S△ABC
=
12
cm2,
则S△ABD
=
.
A
B
C
D
E
F
G
∠2
2.如图,AD,BE,CF
是△ABC
的三条角平分线,则:
∠1
=
;
∠3
=
;
∠ACB
=
2
.
∠ABC
∠4
A
B
C
D
E
F
1
2
3
4
三角形的稳定性
三角形具有稳定性,
四边形没有稳定性.
盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,为什么要这样做呢?
三角形的稳定性
将四边形木架上再钉一根木条,将它的一对顶点连接起来,然后再扭动它,这时木架的形状会改变吗?为什么?
不会改变.钉上的木条将四边形分成两个三角形,而三角形具有稳定性.
斜梁
斜梁
直
梁
三角形的稳定性
如图,工人师傅砌门时,常用木条EF,EG固定门框ABCD,使其不变形,这种做法根据的是三角形的稳定性.
C
E
B
A
F
D
G
三角形的稳定性
四边形不稳定性的应用
活动挂架
1.下列图形中具有稳定性的是(
)
A.正方形
B.长方形
C.直角三角形
D.平行四边形
C
2.要使下列木架稳定各至少需要多少根木棍?
答案:1
2
3
3.你能举例说明三角形的稳定性在实际生活
中的应用吗?
三角形的稳定性的应用举例:
(1)自行车的几个梁形成三角支撑;
(2)钢架桥的钢架做成三角形;
(3)起重机的力臂做成三角形;
(4)照相机的支架做成三角形;
(5)高压电线杆的支架做成三角形.
1.三角形的三条重要线段:高、中线、角平分线.
2.三角形的稳定性.
通过本课时的学习,需要我们掌握:
【解析】选A.四边形没有稳定性.
1.下列设备,没有利用三角形的稳定性的是(
)
A.活动的四边形衣架
B.起重机
C.屋顶三角形钢架
D.索道支架
2.(连云港·中考)小华在电话中问小明:“已知一个三角形三边长分别是4,9,12,如何求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是(
)
【解析】选C.A,D项作的不是三角形的高,B项作的是三角形的高,但不是最长边上的高.
3.如图,在ΔABC中,AE是中线,
AD是角平分线,AF是高.填空:
(1)BE=
=
;
(2)∠BAD=
=
;
(3)∠AFB=
=90°;
(4)SΔABC=
.
CE
BC
∠CAD
∠BAC
∠AFC
BC?AF
4.如图,在△ABC中,
∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,CF⊥AD于H,判断下列说法哪些是正确的,哪些是错误的.
⌒
⌒
A
B
C
D
E
1
2
F
G
H
①AD是△ABE的角平分线(
)
②BE是△
ABD边AD上的中线(
)
③BE是△
ABC边AC上的中线(
)
④CH是△
ACD边AD上的高(
)
三角形的高、中线与角平分线都是线段.
×
×
×
√
理想是指路明星。没有理想,就没有坚定的方向,而没有方向,
就没有生活.
