上海市海滨高中2019-2020学年物理沪科版选修3-5:1.3动量守恒定律的案例分析 课时练(含解析)
文档属性
| 名称 | 上海市海滨高中2019-2020学年物理沪科版选修3-5:1.3动量守恒定律的案例分析 课时练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 610.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-07-17 19:33:04 | ||
图片预览




文档简介
1.3动量守恒定律的案例分析
1.人和气球离地高为h,恰好悬浮在空中,气球质量为M,人的质量为m.人要从气球下拴着的软绳上安全到达地面,软绳的长度至少为( )
A. B. C. D.
2.在光滑水平面上,A、B两球沿同一直线同向运动,碰撞后粘在一起,若碰撞前A、B球的动量分别为6kg·m/s、14kg·m/s,碰撞中B球动量减少6kg·m/s,则A、B两球碰撞前的速度之比为
A.3∶7 B.3∶4
C.2∶7 D.7∶4
3.如图所示,两个小球A、B在光滑水平地面上相向运动,它们的质量分别为 ,速度分别是(设为正方向),则它们发生正碰后,速度的可能值分别为( )
A., B.,
C., D.,
4.沿光滑水平面在同一条直线上运动的两物体A、B碰撞后以共同的速度运动,该过程的位移—时间图象如图所示.则下列判断正确的是( )
A.A、B的质量之比为1:2
B.碰撞前后A的运动方向相同
C.碰撞过程中A的动能变大,B的动能减小
D.碰前B的动量较小
5.相向运动的A、B两辆小车相撞后,一同沿A原来的方向前进,则碰撞前的瞬间(?)
A.A车的动量一定大于B车的动量 B.A车的速度一定大于B车的速度
C.A车的质量一定大于B车的质量 D.A车的动能一定大于B车的动能
6.一质量为m的滑块A以初速度v0沿光滑水平面向右运动,与静止在水平面上的质量为m的滑块B发生碰撞,它们碰撞后一起继续运动,则在碰撞过程中滑块A动量的变化量为( )
A.m v0,方向向左
B.m v0,方向向左
C.m v0,方向向右
D.m v0,方向向右
7.如图所示,一辆小车静止在光滑水平面上,A、B两人分别站在车的两端.当两人同时相向运动时( )
A.若小车不动,两人速率一定相等
B.若小车向左运动,A的速率一定比B的小
C.若小车向左运动,A的动量一定比B的大
D.若小车向左运动,A的动量一定比B的小
8.质量为m的人站在质量为M、长为5米的静止小船的右端,小船的左端靠在岸边(如图所示),当他向左走到船的左端时,船左端离岸的距离是1.25米,则(?? )
A.M=3m B.M=4m C.M=5m D.M=6m
9.质量为m的小球A,沿光滑水平面以速度v0与质量为2m的静止小球B发生正碰,碰撞后,小球A的动能变为原来的,那么小球B的速度可能是( )
A. B. C.v0 D.
10.在光滑水平面上,两球沿球心连线以相等速率相向而行,下列现象可能的是(???? ?? )
A.若两球质量相等,碰后以某一相等速率反向而行
B.若两球质量相等,碰后以某一相等速率同向而行
C.若两球质量不同,碰后以某一相等速率反向而行
D.若两球质量不同,碰后以某一相等速率同向而行
11.一个连同装备总质量为M=100kg的宇航员,在距离飞船x=45m处与飞船处于相对静止状态,宇航员背着装有质量为m0=0.5kg氧气的贮气筒.筒上装有可以使氧气以v=50m/s的速度喷出的喷嘴,宇航员必须向着返回飞船的相反方向放出氧气,才能回到飞船,同时又必须保留一部分氧气供途中呼吸用,宇航员的耗氧率为Q=2.5×10-4 kg/s,不考虑喷出氧气对设备及宇航员总质量的影响,则:
(1)瞬时喷出多少氧气,宇航员才能安全返回飞船?
(2)为了使总耗氧量最低,应一次喷出多少氧气?返回时间又是多少?
12.某静止在水平地面上的炮车水平发射一枚质量为10kg的炮弹,已知炮弹飞出炮口时,相对于地面的速度为900m/s,该炮车质量(不包括炮弹)为3000kg.求:
(1)炮弹飞出炮口时,炮车后退的速度多大;
(2)若炮车后退的距离为1.5m,则炮车后退中受到的阻力与其自身重力的比值为多大(重力加速度取10m/s2).
13.有一艘质量为M=120kg的船停在静水中,船长L=3m,船上一个质量为m=60kg的人从船头走到船尾.不计水的阻力,则船在水中移动的距离为多少?
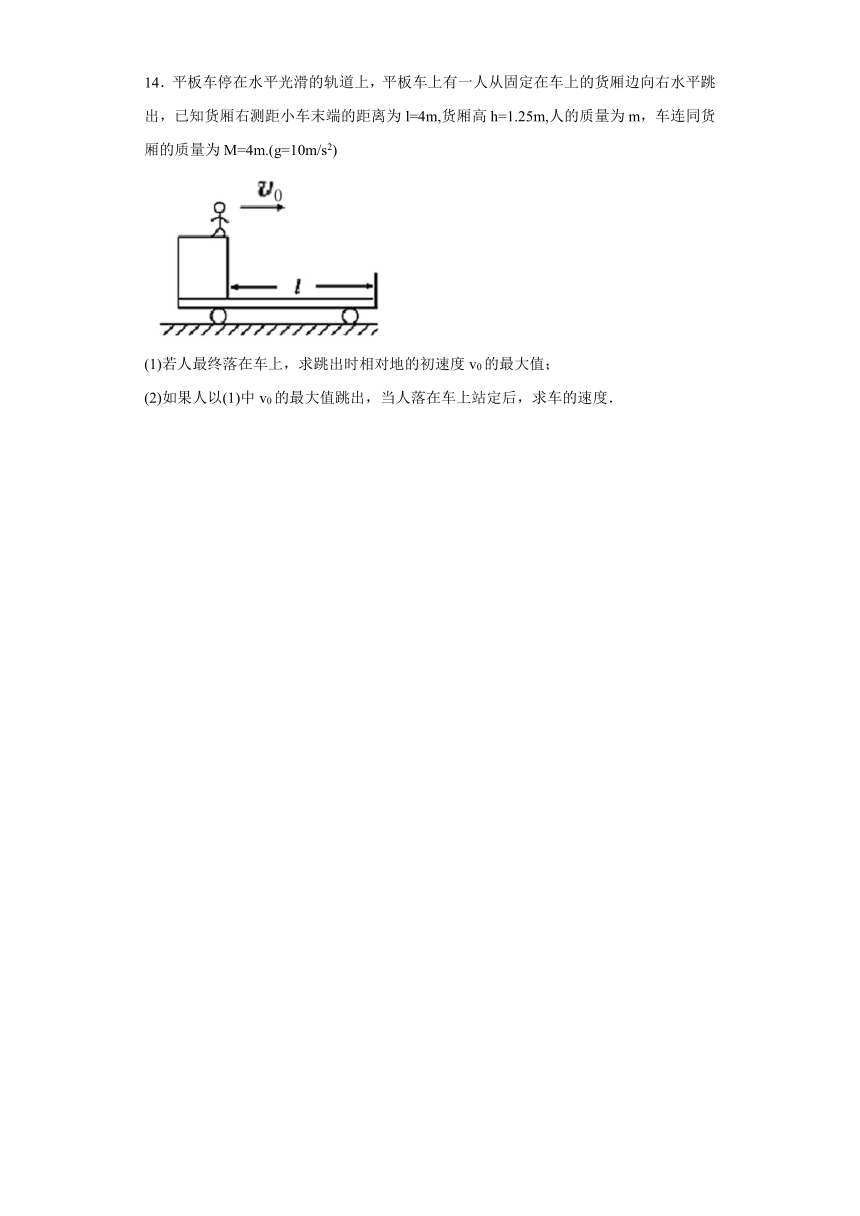
14.平板车停在水平光滑的轨道上,平板车上有一人从固定在车上的货厢边向右水平跳出,已知货厢右测距小车末端的距离为l=4m,货厢高h=1.25m,人的质量为m,车连同货厢的质量为M=4m.(g=10m/s2)
(1)若人最终落在车上,求跳出时相对地的初速度v0的最大值;
(2)如果人以(1)中v0的最大值跳出,当人落在车上站定后,求车的速度.
参考答案
1.D
【解析】
设人沿软绳滑至地面,软绳长度至少为L.以人和气球的系统为研究对象,竖直方向动量守恒,规定竖直向下为正方向,由动量守恒定律得:0=Mv2+mv1…①
人沿绳梯滑至地面时,气球上升的高度为L-h,速度大小:…②
人相对于地面下降的高度为h,速度大小为: …③
将②③代入①得:
解得:;故选D.
2.C
【解析】
设碰前A、B两球速度分别为、,碰撞后粘在一起的速度为,由题意得:、、、,则、,,
,整理得:。故C项正确,ABD三项错误。
3.A
【解析】
两球碰撞过程系统动量守恒,碰撞过程中系统的总动能不可能增加,碰撞后的系统总动能应该小于或等于碰撞前的系统总动能.碰后同向运动时后面小球的速度不可能大于前面小球的速度.由此分析即可.
【详解】
以向右方向为正方向,碰前系统的总动量为:,碰前系统的总动能为:,
A.如果、,碰后系统动量为,碰后系统的总动能为:,可知,系统的动量守恒、动能不增加,符合实际,是可能的,故A正确;B.如果、,碰后系统总动量为,碰后系统的总动能为:,系统的动量守恒,总动能增加,不可能。故B错误;C.如果、,碰后速度方向相反,相向运动,还要发生一次碰撞,这是不可能的。故C错误;D.如果、,碰后总动量为:,碰后系统的总动能为:,系统的动量不守恒,总动能增加不变,不可能的。故D错误;故选A。
【点睛】
对于碰撞过程,往往根据这三个规律去分析:一是系统的动量守恒;二是系统的总动能不增加;三是碰后,不能发生第二次碰撞,若两球分开后同向运动,后面小球的速率不可能大于前面小球的速率.
4.A
【解析】
位移-时间图象的斜率表示速度,由此求出碰撞前后两个物体的速度大小和方向.根据碰撞的基本规律:动量守恒定律求出质量之比.由能量守恒定律比较碰撞两个物体动能的变化.
【详解】
根据位移-时间图象的斜率表示速度,知碰撞前后A的运动方向相反,B正确;碰撞前,A的速度,B的速度为,碰撞后,AB的共同速度为,碰撞前后A的动能不变,B的动能减小,根据动量守恒定律得,解得,A正确C错误;碰撞前,A的动量为,B的动量为,则得,B的动量较大,D错误.
5.A
【解析】
两车相撞过程,系统的动量守恒,相撞后,总动量沿A原来的方向,根据动量守恒定律得知,碰撞前的总动量的方向与A原来的速度方向,由于A.B是相向运动,动量又是矢量,则得,A车的动量一定大于B车的动量.由于两车的质量关系未知,无法判断速度大小、动能大小的关系.故A正确.
故选A
点睛:两车相撞过程,系统的动量守恒,相撞后,总动量沿A原来的速度方向,根据动量守恒定律分析可知,碰撞前的总动量的方向,即可得到两车动量大小的关系.
6.A
【解析】
根据动量守恒定律,设碰后的共同速度为v,则:,解得v=0.6v0;可知在碰撞过程中滑块A动量的变化量为:?P=m×0.6v0-mv0=-0.4mv0,方向向左,故选A.
【点睛】
应用动量守恒定律和动量定理解题时一定要注意正方向的选择,若结果出现负号,说明与正方向相反.
7.C
【解析】
试题分析:AB两人及小车组成的系统不受外力,系统动量守恒,根据动量守恒定律得:
mAvA+mBvB+m车v车=0,若小车不动,则mAvA+mBvB=0,由于不知道AB质量的关系,所以两人速率不一定相等,故A错误;若小车向左运动,则AB的动量和必须向右,而A向右运动,B向左运动,所以A的动量一定比B的大,故B错误,C正确;若小车向右运动,则AB的动量和必须向左,而A向右运动,B向左运动,所以A的动量一定比B的小,故D错误.
考点:本题考查动量守恒.
8.A
【解析】
设人走动时船的速度大小为v,人的速度大小为v′,人从船尾走到船头所用时间为t.取船的速度为正方向.
则 ,,
规定向右为正方向,根据动量守恒得,
即Ml2=m(L﹣l2),
L=5m,l2=1.25m,则M=3m,故A项符合题意,故答案为A.
【点睛】
本题考查动量守恒定律,人船模型,人与船的速度之比等于它们的位移之比,也等于它们的质量反比。
9.AB
【解析】
根据碰后A球的动能恰好变为原来的,即,解得:,碰撞过程中AB动量守恒,则有:mv0=mv+2mvB,解得:或,故AB正确,BC错误。
10.AD
【解析】
A、若两球质量相等,碰撞前以速率相等相向而行,则系统的总动量为零。若碰撞后以某一相等速率反向而行,总动量也为零,符合动量守恒,是可能的;故A正确.
B、若两球质量相等,碰撞前以速率相等相向而行,则系统的总动量为零。若碰后以某一相等速率同向而行,总动量不等于零,不符合动量守恒这一基本规律,不可能发生;故B错误.
C、若两球质量不同,碰撞前以速率相等相向而行,系统的总动量与质量较大的物体动量方向相同;若碰后以某一相等速率反向而行,总动量也与质量较大的物体动量方向相同,而此方向与碰撞前相反,违反了动量守恒定律,不可能发生;故C错误.
D、若两球质量不同,碰撞前以速率相等相向而行,系统的总动量与质量较大的物体动量方向相同;若两球质量不同,碰后以某一相等速率同向而行,总动量可能与碰撞前动量相等,是可能发生的;故D正确.
故选AD.
【点睛】
本题抓住碰撞过程的基本规律:动量守恒定律进行分析,特别要注意动量的方向,动量守恒是指总动量的大小和方向都不变,要正确全面理解.
11.(1) 0.05kg≤m≤0.45kg (2)m=0.15kg,t=600s
【解析】
(1)由题述可知所求的喷出氧气的质量m应有一个范围,若m太小,宇航员获得的速度也小,虽贮气筒中剩余的氧气较多,但由于返回飞船所用的时间太长,将无法满足他途中呼吸所用,若m太大,宇航员获得的速度虽然大了,而筒中氧气太少,也无法满足其呼吸作用,所以m对应的最小和最大两个临界值都应是氧气恰好用完的情况,设瞬间喷气m kg时,宇航员恰能安全返回,根据动量守恒定律可得: mv=MV
宇航员匀速返回的时间为t=x/V
贮气筒中氧气的总质量:m0≥m+Qt
代入数据可得0.05 kg≤m≤0.45 kg
(2)为了使总耗氧量最低,设喷出mkg氧气,则耗氧
又有:
喷气过程动量守恒:
联立可得:,代入式得
根据数学知识有,当时,有最小值,此时m=0.15kg
返回时间
【点睛】
本题考查了动量守恒定律及速度公式的灵活应用,要建立物理模型,理清思路,关键键能从题干中得出和理解有用的信息,如所带氧气质量为m=0.5kg,已知宇航员呼吸的耗氧率为m0=2.5×10-4kg/s等.
12.(1) v=3m/s (2)
【解析】
(1)设炮弹的速度v0、炮车后退的速度大小为v,弹和车的质量分别为m、M,由于内力远大于外力,由动量守恒得:Mv-mv0=0
解得:v=3m/s
(2)设炮车后退中受到的阻力为f、位移为x,由动能定理有:
解得:f=9000N
阻力与其重力的比值:
【点睛】本题主要考查了动量守恒定律的直接应用动能定理的应用,掌握速度的分解和某一方向系统动量守恒.
13.1m
【解析】船和人组成的系统,在水平方向上动量守恒,人在船上行进,船向右退,有mv=MV。人从船头走到船尾,设船后退的位移大小为x,则人相对于岸的位移大小为L-x。由 ;解得,;
点睛:解决本题的关键掌握动量守恒定律的条件,以及知道在运用动量守恒定律时,速度必须相对于地面为参考系.
14.(1)v0=6.4m/s (2) v共=0
【解析】
【详解】
(1)人恰好落到车的右端时人跳出时的速度最大,人跳出过程,人与车组成的系统在水平方向动量守恒,以向右为正方向,由动量守恒定律得:mv0-Mv =0,
即,
可得:x ==3.2m,以地为参考系,人做平抛运动:t==0.5s ,
所以:v0==6.4m/s
(2)人从跳出到落在车上水平方向动量守恒:(M+m)v共=0;
解得:v共=0
点睛:本题要分析清楚物体的运动过程,明确人跳出过程,人与车组成的系统动量守恒.知道平抛运动常用运动的分解法研究.
1.人和气球离地高为h,恰好悬浮在空中,气球质量为M,人的质量为m.人要从气球下拴着的软绳上安全到达地面,软绳的长度至少为( )
A. B. C. D.
2.在光滑水平面上,A、B两球沿同一直线同向运动,碰撞后粘在一起,若碰撞前A、B球的动量分别为6kg·m/s、14kg·m/s,碰撞中B球动量减少6kg·m/s,则A、B两球碰撞前的速度之比为
A.3∶7 B.3∶4
C.2∶7 D.7∶4
3.如图所示,两个小球A、B在光滑水平地面上相向运动,它们的质量分别为 ,速度分别是(设为正方向),则它们发生正碰后,速度的可能值分别为( )
A., B.,
C., D.,
4.沿光滑水平面在同一条直线上运动的两物体A、B碰撞后以共同的速度运动,该过程的位移—时间图象如图所示.则下列判断正确的是( )
A.A、B的质量之比为1:2
B.碰撞前后A的运动方向相同
C.碰撞过程中A的动能变大,B的动能减小
D.碰前B的动量较小
5.相向运动的A、B两辆小车相撞后,一同沿A原来的方向前进,则碰撞前的瞬间(?)
A.A车的动量一定大于B车的动量 B.A车的速度一定大于B车的速度
C.A车的质量一定大于B车的质量 D.A车的动能一定大于B车的动能
6.一质量为m的滑块A以初速度v0沿光滑水平面向右运动,与静止在水平面上的质量为m的滑块B发生碰撞,它们碰撞后一起继续运动,则在碰撞过程中滑块A动量的变化量为( )
A.m v0,方向向左
B.m v0,方向向左
C.m v0,方向向右
D.m v0,方向向右
7.如图所示,一辆小车静止在光滑水平面上,A、B两人分别站在车的两端.当两人同时相向运动时( )
A.若小车不动,两人速率一定相等
B.若小车向左运动,A的速率一定比B的小
C.若小车向左运动,A的动量一定比B的大
D.若小车向左运动,A的动量一定比B的小
8.质量为m的人站在质量为M、长为5米的静止小船的右端,小船的左端靠在岸边(如图所示),当他向左走到船的左端时,船左端离岸的距离是1.25米,则(?? )
A.M=3m B.M=4m C.M=5m D.M=6m
9.质量为m的小球A,沿光滑水平面以速度v0与质量为2m的静止小球B发生正碰,碰撞后,小球A的动能变为原来的,那么小球B的速度可能是( )
A. B. C.v0 D.
10.在光滑水平面上,两球沿球心连线以相等速率相向而行,下列现象可能的是(???? ?? )
A.若两球质量相等,碰后以某一相等速率反向而行
B.若两球质量相等,碰后以某一相等速率同向而行
C.若两球质量不同,碰后以某一相等速率反向而行
D.若两球质量不同,碰后以某一相等速率同向而行
11.一个连同装备总质量为M=100kg的宇航员,在距离飞船x=45m处与飞船处于相对静止状态,宇航员背着装有质量为m0=0.5kg氧气的贮气筒.筒上装有可以使氧气以v=50m/s的速度喷出的喷嘴,宇航员必须向着返回飞船的相反方向放出氧气,才能回到飞船,同时又必须保留一部分氧气供途中呼吸用,宇航员的耗氧率为Q=2.5×10-4 kg/s,不考虑喷出氧气对设备及宇航员总质量的影响,则:
(1)瞬时喷出多少氧气,宇航员才能安全返回飞船?
(2)为了使总耗氧量最低,应一次喷出多少氧气?返回时间又是多少?
12.某静止在水平地面上的炮车水平发射一枚质量为10kg的炮弹,已知炮弹飞出炮口时,相对于地面的速度为900m/s,该炮车质量(不包括炮弹)为3000kg.求:
(1)炮弹飞出炮口时,炮车后退的速度多大;
(2)若炮车后退的距离为1.5m,则炮车后退中受到的阻力与其自身重力的比值为多大(重力加速度取10m/s2).
13.有一艘质量为M=120kg的船停在静水中,船长L=3m,船上一个质量为m=60kg的人从船头走到船尾.不计水的阻力,则船在水中移动的距离为多少?
14.平板车停在水平光滑的轨道上,平板车上有一人从固定在车上的货厢边向右水平跳出,已知货厢右测距小车末端的距离为l=4m,货厢高h=1.25m,人的质量为m,车连同货厢的质量为M=4m.(g=10m/s2)
(1)若人最终落在车上,求跳出时相对地的初速度v0的最大值;
(2)如果人以(1)中v0的最大值跳出,当人落在车上站定后,求车的速度.
参考答案
1.D
【解析】
设人沿软绳滑至地面,软绳长度至少为L.以人和气球的系统为研究对象,竖直方向动量守恒,规定竖直向下为正方向,由动量守恒定律得:0=Mv2+mv1…①
人沿绳梯滑至地面时,气球上升的高度为L-h,速度大小:…②
人相对于地面下降的高度为h,速度大小为: …③
将②③代入①得:
解得:;故选D.
2.C
【解析】
设碰前A、B两球速度分别为、,碰撞后粘在一起的速度为,由题意得:、、、,则、,,
,整理得:。故C项正确,ABD三项错误。
3.A
【解析】
两球碰撞过程系统动量守恒,碰撞过程中系统的总动能不可能增加,碰撞后的系统总动能应该小于或等于碰撞前的系统总动能.碰后同向运动时后面小球的速度不可能大于前面小球的速度.由此分析即可.
【详解】
以向右方向为正方向,碰前系统的总动量为:,碰前系统的总动能为:,
A.如果、,碰后系统动量为,碰后系统的总动能为:,可知,系统的动量守恒、动能不增加,符合实际,是可能的,故A正确;B.如果、,碰后系统总动量为,碰后系统的总动能为:,系统的动量守恒,总动能增加,不可能。故B错误;C.如果、,碰后速度方向相反,相向运动,还要发生一次碰撞,这是不可能的。故C错误;D.如果、,碰后总动量为:,碰后系统的总动能为:,系统的动量不守恒,总动能增加不变,不可能的。故D错误;故选A。
【点睛】
对于碰撞过程,往往根据这三个规律去分析:一是系统的动量守恒;二是系统的总动能不增加;三是碰后,不能发生第二次碰撞,若两球分开后同向运动,后面小球的速率不可能大于前面小球的速率.
4.A
【解析】
位移-时间图象的斜率表示速度,由此求出碰撞前后两个物体的速度大小和方向.根据碰撞的基本规律:动量守恒定律求出质量之比.由能量守恒定律比较碰撞两个物体动能的变化.
【详解】
根据位移-时间图象的斜率表示速度,知碰撞前后A的运动方向相反,B正确;碰撞前,A的速度,B的速度为,碰撞后,AB的共同速度为,碰撞前后A的动能不变,B的动能减小,根据动量守恒定律得,解得,A正确C错误;碰撞前,A的动量为,B的动量为,则得,B的动量较大,D错误.
5.A
【解析】
两车相撞过程,系统的动量守恒,相撞后,总动量沿A原来的方向,根据动量守恒定律得知,碰撞前的总动量的方向与A原来的速度方向,由于A.B是相向运动,动量又是矢量,则得,A车的动量一定大于B车的动量.由于两车的质量关系未知,无法判断速度大小、动能大小的关系.故A正确.
故选A
点睛:两车相撞过程,系统的动量守恒,相撞后,总动量沿A原来的速度方向,根据动量守恒定律分析可知,碰撞前的总动量的方向,即可得到两车动量大小的关系.
6.A
【解析】
根据动量守恒定律,设碰后的共同速度为v,则:,解得v=0.6v0;可知在碰撞过程中滑块A动量的变化量为:?P=m×0.6v0-mv0=-0.4mv0,方向向左,故选A.
【点睛】
应用动量守恒定律和动量定理解题时一定要注意正方向的选择,若结果出现负号,说明与正方向相反.
7.C
【解析】
试题分析:AB两人及小车组成的系统不受外力,系统动量守恒,根据动量守恒定律得:
mAvA+mBvB+m车v车=0,若小车不动,则mAvA+mBvB=0,由于不知道AB质量的关系,所以两人速率不一定相等,故A错误;若小车向左运动,则AB的动量和必须向右,而A向右运动,B向左运动,所以A的动量一定比B的大,故B错误,C正确;若小车向右运动,则AB的动量和必须向左,而A向右运动,B向左运动,所以A的动量一定比B的小,故D错误.
考点:本题考查动量守恒.
8.A
【解析】
设人走动时船的速度大小为v,人的速度大小为v′,人从船尾走到船头所用时间为t.取船的速度为正方向.
则 ,,
规定向右为正方向,根据动量守恒得,
即Ml2=m(L﹣l2),
L=5m,l2=1.25m,则M=3m,故A项符合题意,故答案为A.
【点睛】
本题考查动量守恒定律,人船模型,人与船的速度之比等于它们的位移之比,也等于它们的质量反比。
9.AB
【解析】
根据碰后A球的动能恰好变为原来的,即,解得:,碰撞过程中AB动量守恒,则有:mv0=mv+2mvB,解得:或,故AB正确,BC错误。
10.AD
【解析】
A、若两球质量相等,碰撞前以速率相等相向而行,则系统的总动量为零。若碰撞后以某一相等速率反向而行,总动量也为零,符合动量守恒,是可能的;故A正确.
B、若两球质量相等,碰撞前以速率相等相向而行,则系统的总动量为零。若碰后以某一相等速率同向而行,总动量不等于零,不符合动量守恒这一基本规律,不可能发生;故B错误.
C、若两球质量不同,碰撞前以速率相等相向而行,系统的总动量与质量较大的物体动量方向相同;若碰后以某一相等速率反向而行,总动量也与质量较大的物体动量方向相同,而此方向与碰撞前相反,违反了动量守恒定律,不可能发生;故C错误.
D、若两球质量不同,碰撞前以速率相等相向而行,系统的总动量与质量较大的物体动量方向相同;若两球质量不同,碰后以某一相等速率同向而行,总动量可能与碰撞前动量相等,是可能发生的;故D正确.
故选AD.
【点睛】
本题抓住碰撞过程的基本规律:动量守恒定律进行分析,特别要注意动量的方向,动量守恒是指总动量的大小和方向都不变,要正确全面理解.
11.(1) 0.05kg≤m≤0.45kg (2)m=0.15kg,t=600s
【解析】
(1)由题述可知所求的喷出氧气的质量m应有一个范围,若m太小,宇航员获得的速度也小,虽贮气筒中剩余的氧气较多,但由于返回飞船所用的时间太长,将无法满足他途中呼吸所用,若m太大,宇航员获得的速度虽然大了,而筒中氧气太少,也无法满足其呼吸作用,所以m对应的最小和最大两个临界值都应是氧气恰好用完的情况,设瞬间喷气m kg时,宇航员恰能安全返回,根据动量守恒定律可得: mv=MV
宇航员匀速返回的时间为t=x/V
贮气筒中氧气的总质量:m0≥m+Qt
代入数据可得0.05 kg≤m≤0.45 kg
(2)为了使总耗氧量最低,设喷出mkg氧气,则耗氧
又有:
喷气过程动量守恒:
联立可得:,代入式得
根据数学知识有,当时,有最小值,此时m=0.15kg
返回时间
【点睛】
本题考查了动量守恒定律及速度公式的灵活应用,要建立物理模型,理清思路,关键键能从题干中得出和理解有用的信息,如所带氧气质量为m=0.5kg,已知宇航员呼吸的耗氧率为m0=2.5×10-4kg/s等.
12.(1) v=3m/s (2)
【解析】
(1)设炮弹的速度v0、炮车后退的速度大小为v,弹和车的质量分别为m、M,由于内力远大于外力,由动量守恒得:Mv-mv0=0
解得:v=3m/s
(2)设炮车后退中受到的阻力为f、位移为x,由动能定理有:
解得:f=9000N
阻力与其重力的比值:
【点睛】本题主要考查了动量守恒定律的直接应用动能定理的应用,掌握速度的分解和某一方向系统动量守恒.
13.1m
【解析】船和人组成的系统,在水平方向上动量守恒,人在船上行进,船向右退,有mv=MV。人从船头走到船尾,设船后退的位移大小为x,则人相对于岸的位移大小为L-x。由 ;解得,;
点睛:解决本题的关键掌握动量守恒定律的条件,以及知道在运用动量守恒定律时,速度必须相对于地面为参考系.
14.(1)v0=6.4m/s (2) v共=0
【解析】
【详解】
(1)人恰好落到车的右端时人跳出时的速度最大,人跳出过程,人与车组成的系统在水平方向动量守恒,以向右为正方向,由动量守恒定律得:mv0-Mv =0,
即,
可得:x ==3.2m,以地为参考系,人做平抛运动:t==0.5s ,
所以:v0==6.4m/s
(2)人从跳出到落在车上水平方向动量守恒:(M+m)v共=0;
解得:v共=0
点睛:本题要分析清楚物体的运动过程,明确人跳出过程,人与车组成的系统动量守恒.知道平抛运动常用运动的分解法研究.
同课章节目录
