中考冲刺：尺规作图探究

登陆21世纪教育 助您教考全无忧
中考冲刺：尺规作图探究
一、专题诠释
作图类中考试题，立足基础，突出创新与数学思想方法的考察。纵观2010年全国各地的作图类中考试题，情景型，设计型，阅读型，开放型和网格型，层出不穷，令人目不暇接，与传统教学中的尺规作图相比，中考中的作图题试题开放，联系实际，要求进行多方位，多角度，多层次的探究，考查思维的灵活性，发散性，创新性。
二、解题策略和解法精讲
课程标准对尺规作图的要求是：利用基本作图作三角形，过一点、两点和不在同一直线上的三点作圆。
考试要求：
（1）能完成以下基本作图：作一条线段等于已知线段；作一个角等于已知角；作角的平分线；作线段的垂直平分线。
（2）能利用基本作图作三角形：已知三边作三角形；已知两边及其夹角作三角形；已知两角及其夹边作三角形；已知底边及底边上的高作等腰三角形。
（3）能过一点、两点和不在同一直线上的三点作圆。
（4）了解尺规作图的步骤，对于尺规作图题，会写已知、求作和作法（不要求证明）。
中考尺规作图，抓住基本作图，复杂题简单化。
三、考点精讲
考点一：情景设计型
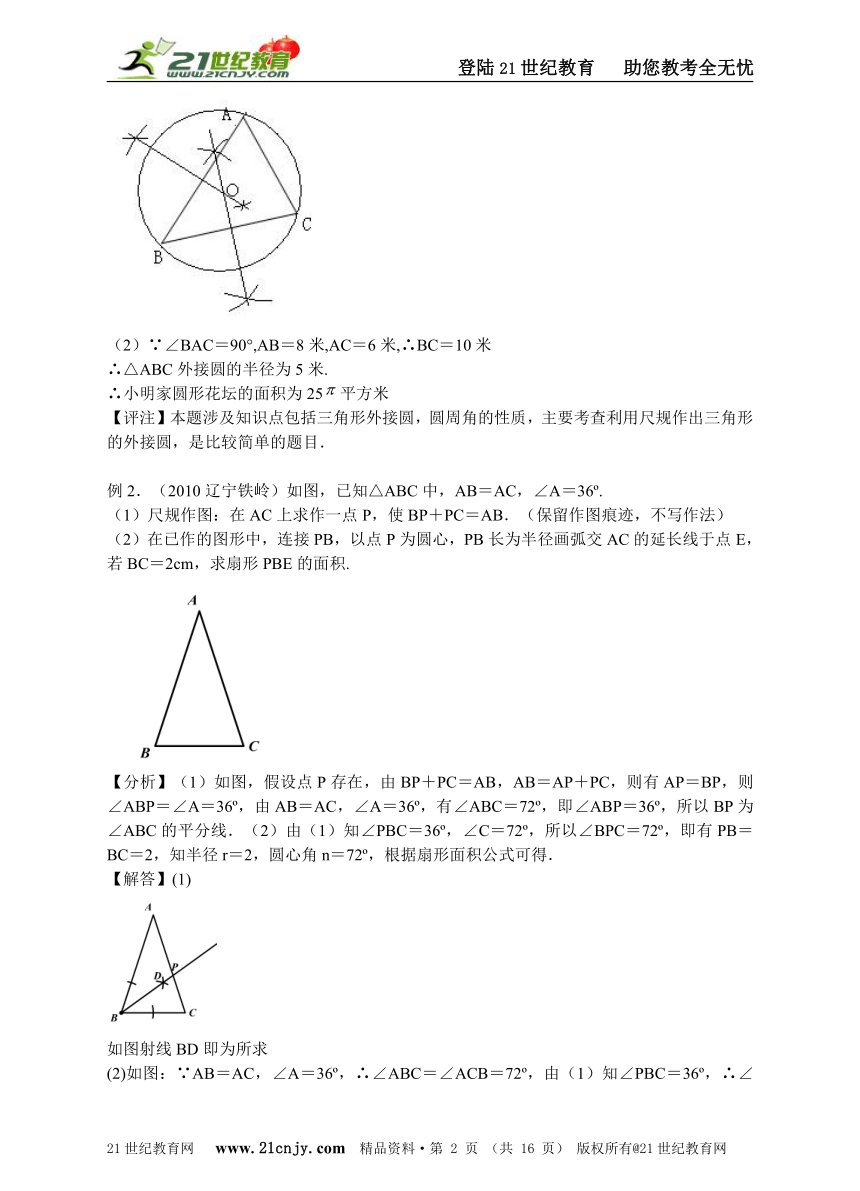
例1．（2010甘肃兰州）小明家的房前有一块矩形的空地，空地上有三棵树A、B、C，小明想建一个圆形花坛，使三棵树都在花坛的边上．
（1）（本小题满分4分）请你帮小明把花坛的位置画出来（尺规作图，不写作法，保留作图痕迹）．
（2）（本小题满分2分））若△ABC中AB＝8米，AC＝6米，∠BAC＝90°，试求小明家圆形花坛的面积．
【分析】（1）根据题意作三角形的外接圆，作出两条边的中垂线，它们的交点为圆心，到顶点的距离为半径；（2）直角三角形的斜边长是外接圆的直径，由勾股定理知斜边BC＝10米.
【解答】(1)用尺规作出两边的垂直平分线
作出圆⊙O即为所求做的花园的位置.如下图
（2）∵∠BAC＝90°,AB＝8米,AC＝6米,∴BC＝10米
∴△ABC外接圆的半径为5米.
∴小明家圆形花坛的面积为25平方米
【评注】本题涉及知识点包括三角形外接圆，圆周角的性质，主要考查利用尺规作出三角形的外接圆，是比较简单的题目．
例2．（2010辽宁铁岭）如图，已知△ABC中，AB＝AC，∠A＝36 .
（1）尺规作图：在AC上求作一点P，使BP＋PC＝AB．（保留作图痕迹，不写作法）
（2）在已作的图形中，连接PB，以点P为圆心，PB长为半径画弧交AC的延长线于点E，若BC＝2cm，求扇形PBE的面积.
【分析】（1）如图，假设点P存在，由BP＋PC＝AB，AB＝AP＋PC，则有AP＝BP，则∠ABP＝∠A＝36 ，由AB＝AC，∠A＝36 ，有∠ABC＝72 ，即∠ABP＝36 ，所以BP为∠ABC的平分线．（2）由（1）知∠PBC＝36 ，∠C＝72 ，所以∠BPC＝72 ，即有PB＝BC＝2，知半径r＝2，圆心角n＝72 ，根据扇形面积公式可得．
【解答】(1)
如图射线BD即为所求
(2)如图：∵AB＝AC，∠A＝36 ，∴∠ABC＝∠ACB＝72 ，由（1）知∠PBC＝36 ，∴∠CBP＝72 ，∴PB＝BC＝2，S扇形PBE＝＝
【评注】本题是一个小综合题，主要考查了等腰三角形、尺规作图、角平分线、扇形的面积公式，属于中档题．在考查学生对知识理解的基础上的分析能力和动手能力．
考点二：网格变换型
例1．（2010江苏镇江）动手操作。在如图所示的方格纸中，△ABC的顶点都在小正方形的顶点上，以小正方形互相垂直的两边所在直线建立直角坐标系.
（1）作出△ABC关于y轴对称的△A1B1C1，其中A，B，C分别和A1，B1，C1对应；
（2）平移△ABC，使得A点在x轴上，B点在y轴上，平移后的三角形记为△A2B2C2，作出平移后的△A2B2C2，其中A，B，C分别和A2，B2，C2对应；
（3）填空：在（2）中，设原△ABC的外心为M，△A2B2C2的外心为M2，则M与M2之间的距离为.
【分析】（1）根据轴对称的作图方法，便可作出△ABC关于y轴对称的△A1B1C1，（2）点B向左平移1格便可到y轴上，点A只要向下平移4格能到x轴上，所以整个图形向左平移1格，再向下平移4格就能使点A到x轴上，点B到y轴上．（3）外心平移的距离与△ABC上任意一点平移的距离相等，所以MM2＝BB2＝
【解答】（1）如下图；
（2）如下图；
（3）
【评注】轴对称、平移作图经常在网格中来实现，作图方便，又能体现学生活学活用相关知识的能力，是近几年来新兴的试题．
例2．（2010广东汕头）如图，方格纸中的每个小方格都是边长为1个单位的正方形，Rt△ABC的顶点均在格点上，在建立平面直角坐标系后，点A的坐标为（－6，1），点B的坐标为（－3，1），点C的坐标为（－3，3）．
（1）将Rt△ABC沿x轴正方向平移5个单位得到Rt△A1B1C1，试在图上画出的图形Rt△A1B1C1，并写出点A1的坐标；
（2）将原来的Rt△ABC绕点B顺时针旋转90°得到Rt△A2B2C2，试在图上画出Rt△A2B2C2的图形．
【分析】将A、B、C三点向右平5个单位后得A1、B1、C1，顺次连接平移后的三点即得平移后的图形；同样将A、C两点绕点B顺时针旋转90°得到A2、C2，顺次连接A2、B、C2三点得到旋转后的图形．
【解答】（1）A（－1，1），如下图；（2）如下图．
【评注】本题主要考查几何变换中的平移与旋转相关知识，只要理解与掌握平移及旋转的定义及性质，作出几何变换后的图形就非常容易了．实际上，图形的变换就是转化为关键点的变换，抓住平移的两要素（平移的方向与距离）与旋转的三要素（旋转中心、旋转方向和旋转角），是解决本题的关键．
考点三：开放探究型
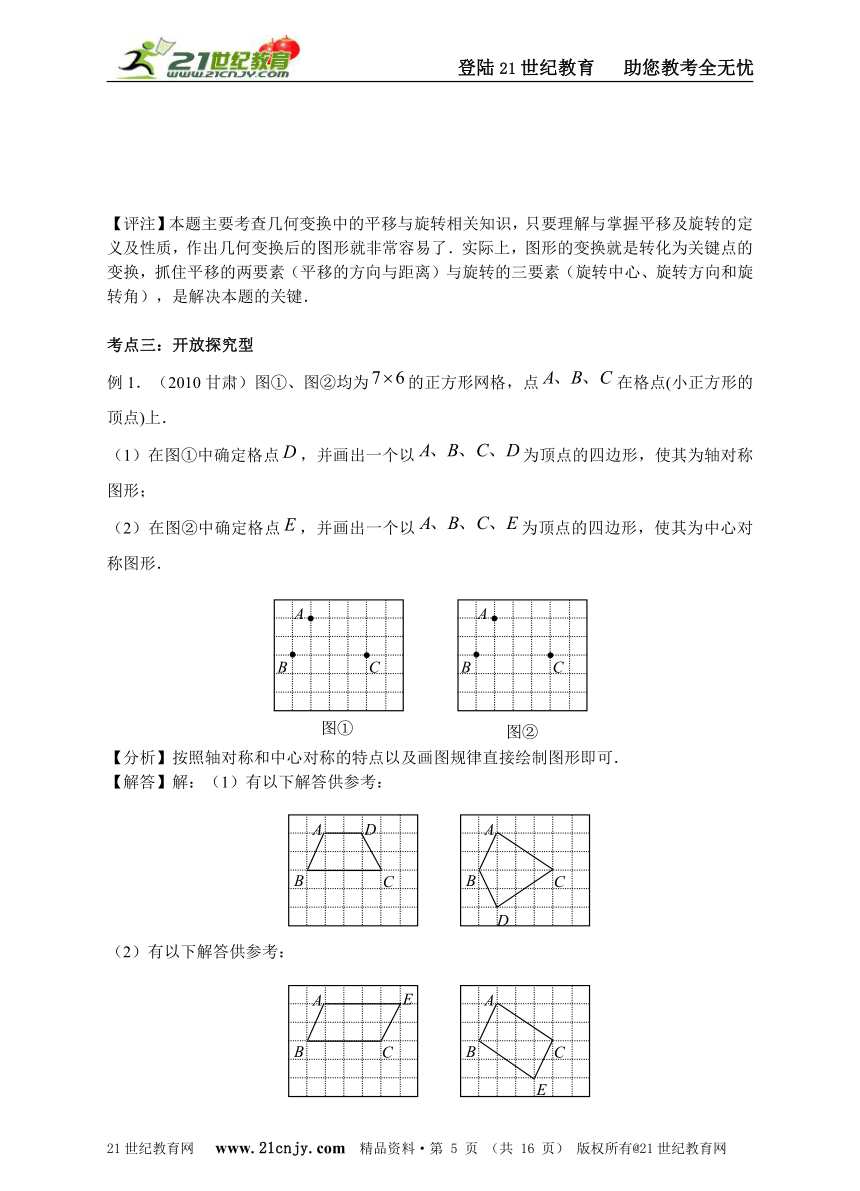
例1．（2010甘肃）图①、图②均为的正方形网格，点在格点(小正方形的顶点)上．
（1）在图①中确定格点，并画出一个以为顶点的四边形，使其为轴对称图形；
（2）在图②中确定格点，并画出一个以为顶点的四边形，使其为中心对称图形．
【分析】按照轴对称和中心对称的特点以及画图规律直接绘制图形即可．
【解答】解：（1）有以下解答供参考：
（2）有以下解答供参考：
【评注】本题主要考查学生对轴对称和中心对称概念的掌握是否全面以及画图能力的培养，信度与效度指标设置合理．
例2．（2010河北）如图11－1，正方形ABCD是一个6×6网格电子屏的示意图，其中每个小正方形的边长为1．位于AD中点处的光点P按图11－2的程序移动．
（1）请在图11－1中画出光点P经过的路径；
（2）求光点P经过的路径总长（结果保留π）．
【分析】（1）以图解的形式呈现运动过程，需要学生理解题意，在网格中画出运动图象，通过判断知此路径为弧（2）利用弧长公式计算四条弧总长
【解答】解：（1）如图1；
（2）∵，∴点P经过的路径总长为6π．
【评注】此题设计新颖，把函数、画图、求弧长等知识融合在一起考查，给人耳目一新之感．
四．真题演练
1.（2010年青海西宁中考题）如图，在△中，AD⊥BC，垂足为D．
（1）尺规作图（不写作法，保留作图痕迹）：作△的外接圆⊙O，作直径AE，连接BE．
（2）若AB＝8，AC＝6，AD＝5，求直径AE的长．（证明△∽△．）
2．（2010年辽宁本溪中考题）如图7，在边长为1的小正方形组成的网格中，△ABC的顶点均在格点上，请按要求完成下列各题：
（1）以直线BC为对称轴作△ABC的轴对称图形，得到△A1BC，再将△A1BC绕着点B逆时针旋转90°，得到△A2BC1，请依此画出△A1BC、△A2BC1；
（2）求线段BC旋转到BC1过程中所扫过的面积（计算结果用π表示）.
SHAPE \* MERGEFORMAT
图7
3.（2010年吉林长春中考题）（1）在图①中。以线段m为一边画菱形，要求菱形的顶点均在格点上。（画一个即可）
（2）在图②中，平移a、b、c中的两条线段，使它们与线段n构成以n为一边的等腰直角三角形。（画一个即可）
【答案】
1.（1）如下图
（2）因为AB是直径，
所以∠ABE＝90°．
因为AD⊥BC，所以∠ADC＝∠ABE＝90°．
所以△∽△．
所以．
即．
所以AE＝．
2.解：（1）如图所示：
（2）BC旋转到BC1时旋转角为90°，半径为4．
∴旋转过程中所扫过的面积为＝4π．
答：线段BC旋转到BC1过程中所扫过的面积为4π．
3.解：（１）以下解答共参考
（2）以下解答供参考：
第二部分 练习部分
1.（2010年重庆江津中考题）如图，有分别过A、B两个加油站的公路、相交于点O，现准备在∠AOB内建一个油库，要求油库的位置点P满足到A、B两个加油站的距离相等，而且P到两条公路、的距离也相等。请用尺规作图作出点P（不写作法，保留作图痕迹）．
2.（2010年湖南株洲中考题）如图所示的正方形网格中，网格线的交点称为格点．已知、是两格点，如果也是图中的格点，且使得为等腰三角形，则点的个数是（）
A．6 B．7 C．8 D．9
3.（2010年山东威海中考题）如图，点A，B，C的坐标分别为（2，4），（5，2），（3，－1）．若以点A，B，C，D为顶点的四边形既是轴对称图形，又是中心对称图形，则点D的坐标为．
4.（2010年云南昆明中考题）在如图所示的直角坐标系中，解答下列问题：
（1）分别写出A、B两点的坐标；
（2）将△ABC绕点A顺时针旋转90°，画出旋转后的△AB1C1；
（3）求出线段B1A所在直线l的函数解析式，并写出在直线l上从B1到A的自变量x　的取值范围.
5.（2010湖南长沙中考题）△ABC在平面直角坐标系中的位置如图所示，A、B、C三点在格点上．
（１）作出△ABC关于ｙ轴对称的△，并写出点的坐标；
（２）作出△ABC关于原点O对称的△，并写出点的坐标．
6． ( 2010中考精品分类汇编 )（2010年青海中考题）梯形ABCD的四个顶点分别为A（0,6），B（2,2），C（4,2）D（6,6）．按下列要求画图．
（1）在平面直角坐标系中，画出以原点O为位似中心，相似比为的位似图形；
（2）画出位似图形向下平移五个单位长度后的图形 ．
7．（2010年浙江嵊州中考题）
（1）请在图①的正方形ABCD内，画出使∠APB＝90°的一个点P，并说明理由。
（2）请在图②的正方形ABCD内（含边），画出使∠APB＝60°的所有的点P，并说明理由。
（3）如图③，现在一块矩形钢板ABCD，AB＝4，BC＝3，工人师傅想用它裁出两块全等的、面积最大的△APB和△CPD钢板，且∠APB＝∠CPD＝60°，请你在图③中画出符合要求的点P和P。
8． ( 江苏刘东升 )（2010湖北宜昌中考题）如图，已知Rt△ABC和Rt△EBC，°。以边AC上的点O为圆心、OA为半径的⊙O与EC相切，D为切点，AD//BC。
（1）用尺规确定并标出圆心O；（不写做法和证明，保留作图痕迹）
（2）求证：[]
（3）若AD=1，，求BC的长。
【答案】
1.
2.C
3.根据题意，四边形ABCD是矩形或菱形，根据已知坐标用勾股定理算得AB＝，BC＝，AC＝,故∠ABC＝90°，AC＝BC，只有AB、BC作为四边形的边长，AC作为对角线的正方形ABCD（见下图）才符合条件，∵点B移到点C，向左移2个单位，下移2个单位，又ADBC,∴点D的坐标为（2－2，4－3）即（0，1）．
4.解：（1）A(2，0)，B(-1,-4)
（2）画图正确
(3)设线段B1A所在直线l的解析式为：
∵B1(-2,3),A(2,0)
∴
∴线段B1A所在直线l的解析式为：
线段B1A的自变量x的取值范围是：-2≤x≤2
5.（１）（２）如图，点的坐标（－3，2）；点的坐标（－3，－2）．
6.解：（1）把原图形缩小到原来的，也就是使新图形上各顶点到位似中心的距离与原图形各对应顶点到位似中心的距离之比为1∶2；（2）向下平移五个单位长度也就是纵坐标相应的减5．
（1）图形正确得4分
（2）图形正确得3分
7.解：（1）如图①，根据正方形的对角线相互垂直，所以可以连接对角线，交点为点P；
连接AC、BD交于点P，则∠APB＝90°，
∴点P为所求，
（2）如图②，画法如下：
1）以AB为边在正方形内作等边△ABP；
2）作△ABP的外接圆⊙O，分别与AD、BC交于点E、F．
∵在⊙O中，弦AB所对的弧APB上的圆周角均为60°，
∴弧EF上的所有点均为所求的点P，
（3）如图③，画法如下：
1）连接AC；
2）以AB为边作等边△ABE；
3）作等边△ABE的外接圆⊙O，交AC于点P；
4）在AC上截取AP’＝CP．
则点P、P’为所求．
过点B作BG⊥AC，交AC于点G．
∵在Rt△ABC中，AB＝4，BC＝3，
∴AC＝．
∴BG＝．
在Rt△ABG中，AB＝4，
∴AG＝．
在Rt△BPG中，∠BPA＝60°，
∴PG＝，
∴AP＝AG+PG＝．
∴S△APB＝
8. 解：（1）过D点作EC的垂线与AC的交点即Ｏ；（提示：O即为AD中垂线与AC的交点或过D点作EC的垂线与AC的交点等）.
能见作图痕迹，作图基本准确即可．
（2）证明:连结OD．∵AD∥BC，∠B=90°，∴∠EAD=90°．
∴∠E+∠EDA=90°，即∠E=90°－∠EDA．
又圆O与EC相切于D点，∴OD⊥EC．
∴∠EDA+∠ODA=90°，即∠ODA=90°－∠EDA．
∴∠E=∠ODA
又OD=OA，∴∠DAC=∠ODA，∴∠DAC=∠E．
∵AD∥BC，∴∠DAC=∠ACB，∴∠E=∠ACB．
（3）Rt△DEA中，tan∠E=，又tan∠E=tan∠DAC=，
∵AD=1∴EA=．
Rt△ABC中，tan∠ACB=，
又∠DAC=∠ACB，∴tan∠ACB=tan∠DAC．
∴=，∴可设．
∵AD∥BC，∴Rt△EAD∽Rt△EBC．
∴，即．
∴，∴．
C1
B1
图
C1
A2
A1
C
B
A
C
B
A
P
C
B
图1
D
A
绕点D顺时针旋转90°
输出点
输入点P
图11－2
绕点C顺时针旋转90°
绕点B顺时针旋转90°
绕点A顺时针旋转90°
P
C
B
图11－1
D
A
E
C
B
A
E
C
B
A
C
D
C
B
A
D
B
A
图②
C
B
A
图①
C
B
A
O
-1
1
1
C
B
y
x
A
第13题图
B
C
A
O
x
y
C2
B2
A2
B1
C1
A1
B
C
A
O
x
y
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 （共 16 页） 版权所有@21世纪教育网