9.1.1 不等式及其解集(含答案)-
文档属性
| 名称 | 9.1.1 不等式及其解集(含答案)- |
|
|
| 格式 | zip | ||
| 文件大小 | 45.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-16 00:00:00 | ||
图片预览

文档简介
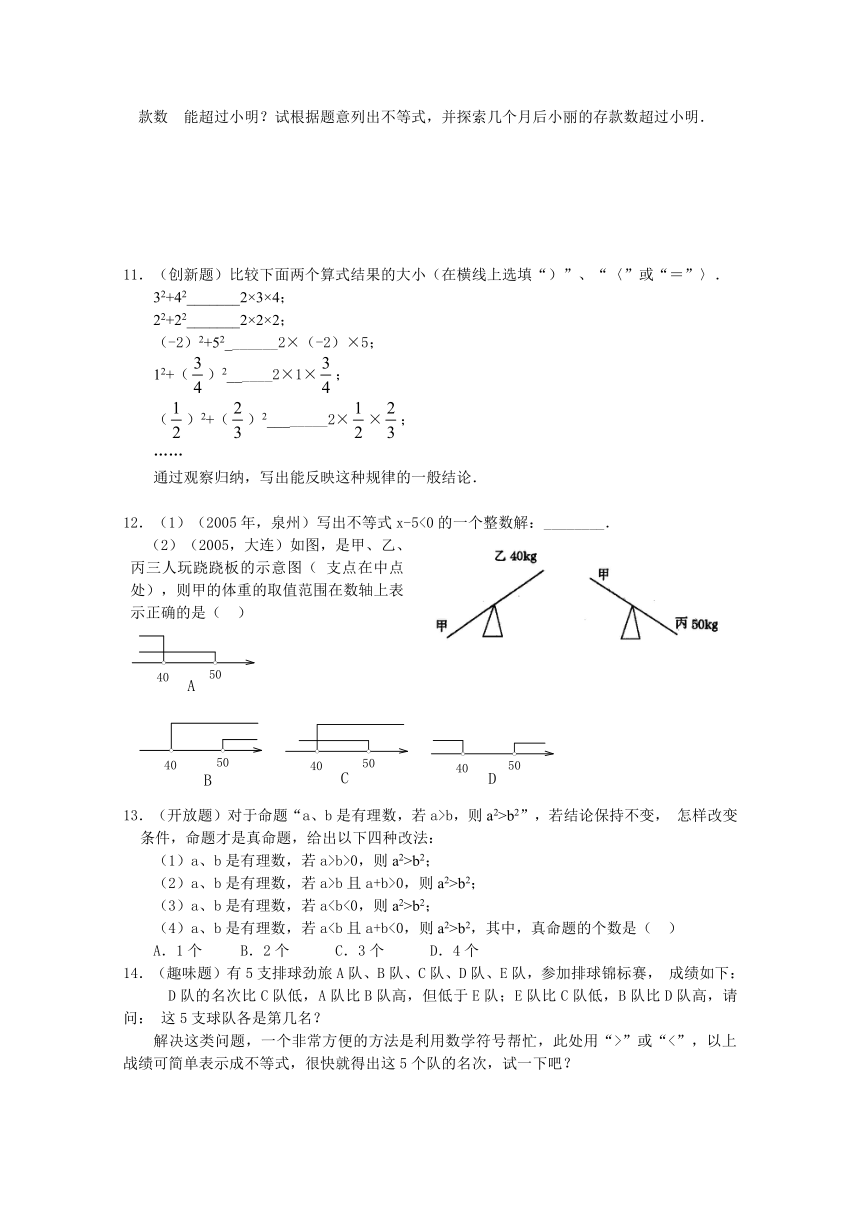
9.1.1 不等式及其解集
1.用不等式表示:
(1)a的2倍与4的差是正数; (2)b的与c的和是负数;
(3)x与y的差是非负数; (4)a的与15的和的是负数;
(5)x的绝对值与1的和不小于1;(6)a的20%与a的和不大于a的2倍与1的差.
2.(2010年湖南郴州市)不等式的解集是_________.
3.(2010·浙江温州)把不等式x+2>4的解表示在数轴上,正确的是( )
4.下图表示的是不等式( )的解集.
A.x>- B.x≥- C.x<- D.x≤-
5.已知实数a、b在数轴上对应的点如图所示,则下列式子正确的是( )
A.ab>0 B.│a│>│b│ C.a-b>0 D.a+b>0
6.设“●”、“▲”、“■”表示三种不同的物体.现用天平称两次,情况如图所示,那么●、▲、■这三种物体质量从大到小的顺序排列正确的是( )
A.■、●、▲ B.■、▲、●
C.▲、●、■ D.▲、■、●
7.满足x+2≤4的非负整数是__________.
8.直接写出不等式的解集:
(1)x+2>4; (2)3x<6; (3)x-5>0.
9.a是有理数,a2+3的最小值是_______;1-a2的最大值是_______;
(a-1)2+5的最小值是________;9-(a+2)2的最大值是_________.
10.(应用题)小明和小丽决定把省下来的零用钱存起来,这个月小明存了168元,小丽存了85元,从下个月开始小明每月存16元,而小丽每月存25元.问:几个月后小丽的存款数 能超过小明?试根据题意列出不等式,并探索几个月后小丽的存款数超过小明.
11.(创新题)比较下面两个算式结果的大小(在横线上选填“)”、“〈”或“=”〉.
32+42_______2×3×4;
22+22_______2×2×2;
(-2)2+52_______2×(-2)×5;
12+()2______2×1×;
()2+()2________2××;
……
通过观察归纳,写出能反映这种规律的一般结论.
12.(1)(2005年,泉州)写出不等式x-5<0的一个整数解:________.
(2)(2005,大连)如图,是甲、乙、丙三人玩跷跷板的示意图(支点在中点处),则甲的体重的取值范围在数轴上表示正确的是( )
13.(开放题)对于命题“a、b是有理数,若a>b,则a2>b2”,若结论保持不变,怎样改变条件,命题才是真命题,给出以下四种改法:
(1)a、b是有理数,若a>b>0,则a2>b2;
(2)a、b是有理数,若a>b且a+b>0,则a2>b2;
(3)a、b是有理数,若ab2;
(4)a、b是有理数,若ab2,其中,真命题的个数是( )
A.1个 B.2个 C.3个 D.4个
14.(趣味题)有5支排球劲旅A队、B队、C队、D队、E队,参加排球锦标赛,成绩如下:
D队的名次比C队低,A队比B队高,但低于E队;E队比C队低,B队比D队高,请问:这5支球队各是第几名?
解决这类问题,一个非常方便的方法是利用数学符号帮忙,此处用“>”或“<”,以上战绩可简单表示成不等式,很快就得出这5个队的名次,试一下吧?
15.德国数学家高斯写日记时有一个习惯,即把生活中发生重大事件的日子写成密码,就是写出由自己生日到这个日子的天数,例如1799年7月16日,高斯博士论文答辩,他把这一天记作8113.
在高斯的日记中第一次就这样记下的日子是他15岁时解决质数分布问题的那一天,他把这一天记作5343.
聪明的同学,你知道高斯是哪年哪月哪日解决质数分布问题的吗?
答案:
1.(1)2a-4>0;(2)b+c<0;(3)x-y≥0;(4)(a+15)<0;
(5)│x│+1≥1;(6)20%a+a≤2a-1.
2.
3.B 4.B 5.C 6.B 7.0,1,2
8.(1)x>2; (2)x<2; (3)x<5.
9.3;1;5;9
点拨:∵a2≥0,(a-1)2≥0,(a+2)2≥0,
∴a2+3≥3,1-a2≤1,(a-1)2+5≥5,
9-(a+2)2≤9.
∴a2+3的最小值是3;1-a2的最大值为1;
(a-1)2+5的最小值为5;9-(a+2)2的最大值是9.
10.解:设x个月后小丽的存款数超过小明.依题意,得
25x+85>16x+168.
探索得10个月后小丽的存款数超过小明.
11.解:横线上依次填写>;=;>;>;>
一般结论为:a2+b2≥2ab(当a=b时取等号).
12.(1)略 (2)C
13.D 点拨:可逐一推断或举反例.
14.C>E>A>B>D(1,2,3,4,5名).
15.1791年12月15日.
1.用不等式表示:
(1)a的2倍与4的差是正数; (2)b的与c的和是负数;
(3)x与y的差是非负数; (4)a的与15的和的是负数;
(5)x的绝对值与1的和不小于1;(6)a的20%与a的和不大于a的2倍与1的差.
2.(2010年湖南郴州市)不等式的解集是_________.
3.(2010·浙江温州)把不等式x+2>4的解表示在数轴上,正确的是( )
4.下图表示的是不等式( )的解集.
A.x>- B.x≥- C.x<- D.x≤-
5.已知实数a、b在数轴上对应的点如图所示,则下列式子正确的是( )
A.ab>0 B.│a│>│b│ C.a-b>0 D.a+b>0
6.设“●”、“▲”、“■”表示三种不同的物体.现用天平称两次,情况如图所示,那么●、▲、■这三种物体质量从大到小的顺序排列正确的是( )
A.■、●、▲ B.■、▲、●
C.▲、●、■ D.▲、■、●
7.满足x+2≤4的非负整数是__________.
8.直接写出不等式的解集:
(1)x+2>4; (2)3x<6; (3)x-5>0.
9.a是有理数,a2+3的最小值是_______;1-a2的最大值是_______;
(a-1)2+5的最小值是________;9-(a+2)2的最大值是_________.
10.(应用题)小明和小丽决定把省下来的零用钱存起来,这个月小明存了168元,小丽存了85元,从下个月开始小明每月存16元,而小丽每月存25元.问:几个月后小丽的存款数 能超过小明?试根据题意列出不等式,并探索几个月后小丽的存款数超过小明.
11.(创新题)比较下面两个算式结果的大小(在横线上选填“)”、“〈”或“=”〉.
32+42_______2×3×4;
22+22_______2×2×2;
(-2)2+52_______2×(-2)×5;
12+()2______2×1×;
()2+()2________2××;
……
通过观察归纳,写出能反映这种规律的一般结论.
12.(1)(2005年,泉州)写出不等式x-5<0的一个整数解:________.
(2)(2005,大连)如图,是甲、乙、丙三人玩跷跷板的示意图(支点在中点处),则甲的体重的取值范围在数轴上表示正确的是( )
13.(开放题)对于命题“a、b是有理数,若a>b,则a2>b2”,若结论保持不变,怎样改变条件,命题才是真命题,给出以下四种改法:
(1)a、b是有理数,若a>b>0,则a2>b2;
(2)a、b是有理数,若a>b且a+b>0,则a2>b2;
(3)a、b是有理数,若a
(4)a、b是有理数,若a
A.1个 B.2个 C.3个 D.4个
14.(趣味题)有5支排球劲旅A队、B队、C队、D队、E队,参加排球锦标赛,成绩如下:
D队的名次比C队低,A队比B队高,但低于E队;E队比C队低,B队比D队高,请问:这5支球队各是第几名?
解决这类问题,一个非常方便的方法是利用数学符号帮忙,此处用“>”或“<”,以上战绩可简单表示成不等式,很快就得出这5个队的名次,试一下吧?
15.德国数学家高斯写日记时有一个习惯,即把生活中发生重大事件的日子写成密码,就是写出由自己生日到这个日子的天数,例如1799年7月16日,高斯博士论文答辩,他把这一天记作8113.
在高斯的日记中第一次就这样记下的日子是他15岁时解决质数分布问题的那一天,他把这一天记作5343.
聪明的同学,你知道高斯是哪年哪月哪日解决质数分布问题的吗?
答案:
1.(1)2a-4>0;(2)b+c<0;(3)x-y≥0;(4)(a+15)<0;
(5)│x│+1≥1;(6)20%a+a≤2a-1.
2.
3.B 4.B 5.C 6.B 7.0,1,2
8.(1)x>2; (2)x<2; (3)x<5.
9.3;1;5;9
点拨:∵a2≥0,(a-1)2≥0,(a+2)2≥0,
∴a2+3≥3,1-a2≤1,(a-1)2+5≥5,
9-(a+2)2≤9.
∴a2+3的最小值是3;1-a2的最大值为1;
(a-1)2+5的最小值为5;9-(a+2)2的最大值是9.
10.解:设x个月后小丽的存款数超过小明.依题意,得
25x+85>16x+168.
探索得10个月后小丽的存款数超过小明.
11.解:横线上依次填写>;=;>;>;>
一般结论为:a2+b2≥2ab(当a=b时取等号).
12.(1)略 (2)C
13.D 点拨:可逐一推断或举反例.
14.C>E>A>B>D(1,2,3,4,5名).
15.1791年12月15日.
