《空间点、直线、平面之间的位置关系》
文档属性
| 名称 | 《空间点、直线、平面之间的位置关系》 |

|
|
| 格式 | rar | ||
| 文件大小 | 266.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-06-09 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
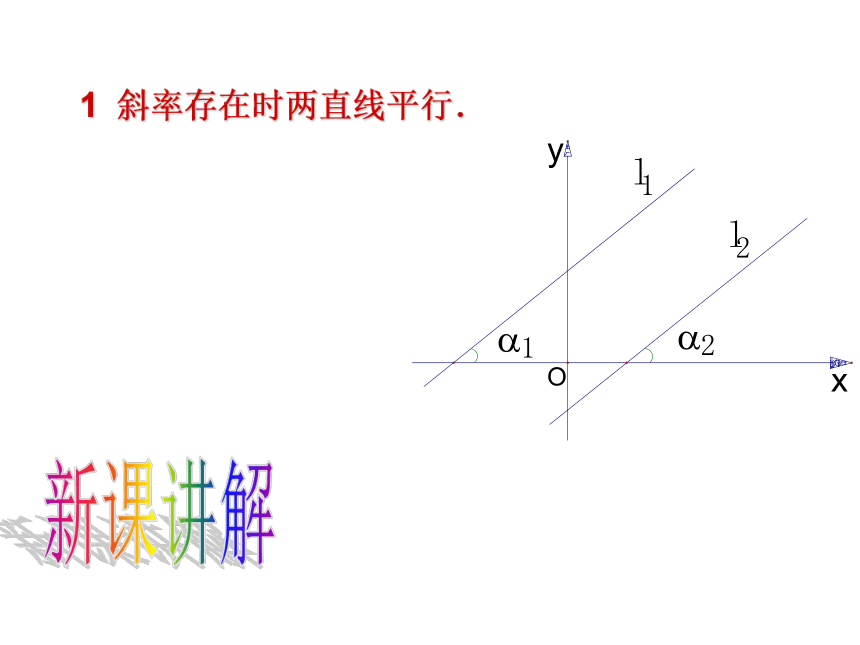
1 斜率存在时两直线平行.
结论1:
如果直线L1,L2的斜率为k1,k2.
那么
L1∥L2 k1=k2
注意:上面的等价是在两直线斜率存在的前提下才成立的,
缺少这个前提,结论并不存立.
特殊情况下的两直线平行:
两直线的倾斜角都为90°,互相平行.
例题讲解
例1
例2
例3:
求与直线2x+3y+5=0平行,且在两坐标轴上的截距之
和为 的直线的方程.
6
5
一般地,直线Ax+By+C=0中系数A、B确定直线的斜率,
因此,与直线Ax+By+C=0平行的直线方程可设为Ax+By+ =0 ,
其中 待定(直线系)
1 若直线 和 平行,则 = 。
a
1
2
=
-
ay
x
1
2
2
=
-
ay
x
0
2 若直线 和 平行,则 = 。
a
1
+
=
+
a
y
ax
2
2
+
=
+
a
ay
x
1
0
4
6
=
+
-
C
y
x
0
1
2
=
-
-
y
Ax
直线 和直线 平行
的条件是 。
2 斜率存在时两直线垂直.
结论2:
如果两直线的斜率为k1, k2,那么,这两条直线垂直
的充要条件是k1·k2= -1
注意:上面的等价是在两直线斜率存在的前提下才成立的,
缺少这个前提,结论并不存立.
特殊情况下的两直线平行与垂直.
当两条直线中有一条直线没有斜率时:
当另一条直线的斜率为0时,
则一条直线的倾斜角为900,另一条直线的倾斜角为0°
两直线互相垂直
例4 已知直线 与
互相垂直,求 的值
0
2
)
3
2
(
)
1
(
=
+
+
+
-
y
a
x
a
0
3
)
1
(
)
2
(
=
-
-
+
+
y
a
x
a
例5:
求过点A(2,1)且与直线2x+y-10=0垂直的直线的方程
注意:
①解法一求直线方程的方法是通法,必须掌握;
②解法二是常常采用的解题技巧:
一般地,由于与直线Ax+By+C=0垂直的直线的斜率互为负
倒数,故可得其方程为Bx-Ay+ =0 ,其中 待定(直线系)
2 如果直线L1,L2的方程为
L1:A1x+B1y+C1=0,
L2:A2x+B2y+C2=0(A1B1C1≠0,A2B2C2≠0)
那么L1⊥L2的充要条件是A1A2+B1B2=1
1 如果直线L1,L2的方程为
L1:A1x+B1y+C1=0,
L2:A2x+B2y+C2=0(A1B1C1≠0,A2B2C2≠0)
那么L1∥L2的充要条件是
2
1
2
1
2
1
C
C
B
B
A
A
=
如果直线L1,L2的斜截式方程为L1:y=k1x+b1,L2:y=k2x+b2,
那么L1∥L2 k1=k2且b1≠b2
例1:
两条直线L1:2x-4y+7=0,L2:x-2y+5=0求证:L1∥L2
例2:
求过点A(1,-4)且与直线2x+3y+5=0平行的直线的方程。
注意:
①解法一求直线方程的方法是通法,必须掌握;
②解法二是常常采用的解题技巧。
1 斜率存在时两直线平行.
结论1:
如果直线L1,L2的斜率为k1,k2.
那么
L1∥L2 k1=k2
注意:上面的等价是在两直线斜率存在的前提下才成立的,
缺少这个前提,结论并不存立.
特殊情况下的两直线平行:
两直线的倾斜角都为90°,互相平行.
例题讲解
例1
例2
例3:
求与直线2x+3y+5=0平行,且在两坐标轴上的截距之
和为 的直线的方程.
6
5
一般地,直线Ax+By+C=0中系数A、B确定直线的斜率,
因此,与直线Ax+By+C=0平行的直线方程可设为Ax+By+ =0 ,
其中 待定(直线系)
1 若直线 和 平行,则 = 。
a
1
2
=
-
ay
x
1
2
2
=
-
ay
x
0
2 若直线 和 平行,则 = 。
a
1
+
=
+
a
y
ax
2
2
+
=
+
a
ay
x
1
0
4
6
=
+
-
C
y
x
0
1
2
=
-
-
y
Ax
直线 和直线 平行
的条件是 。
2 斜率存在时两直线垂直.
结论2:
如果两直线的斜率为k1, k2,那么,这两条直线垂直
的充要条件是k1·k2= -1
注意:上面的等价是在两直线斜率存在的前提下才成立的,
缺少这个前提,结论并不存立.
特殊情况下的两直线平行与垂直.
当两条直线中有一条直线没有斜率时:
当另一条直线的斜率为0时,
则一条直线的倾斜角为900,另一条直线的倾斜角为0°
两直线互相垂直
例4 已知直线 与
互相垂直,求 的值
0
2
)
3
2
(
)
1
(
=
+
+
+
-
y
a
x
a
0
3
)
1
(
)
2
(
=
-
-
+
+
y
a
x
a
例5:
求过点A(2,1)且与直线2x+y-10=0垂直的直线的方程
注意:
①解法一求直线方程的方法是通法,必须掌握;
②解法二是常常采用的解题技巧:
一般地,由于与直线Ax+By+C=0垂直的直线的斜率互为负
倒数,故可得其方程为Bx-Ay+ =0 ,其中 待定(直线系)
2 如果直线L1,L2的方程为
L1:A1x+B1y+C1=0,
L2:A2x+B2y+C2=0(A1B1C1≠0,A2B2C2≠0)
那么L1⊥L2的充要条件是A1A2+B1B2=1
1 如果直线L1,L2的方程为
L1:A1x+B1y+C1=0,
L2:A2x+B2y+C2=0(A1B1C1≠0,A2B2C2≠0)
那么L1∥L2的充要条件是
2
1
2
1
2
1
C
C
B
B
A
A
=
如果直线L1,L2的斜截式方程为L1:y=k1x+b1,L2:y=k2x+b2,
那么L1∥L2 k1=k2且b1≠b2
例1:
两条直线L1:2x-4y+7=0,L2:x-2y+5=0求证:L1∥L2
例2:
求过点A(1,-4)且与直线2x+3y+5=0平行的直线的方程。
注意:
①解法一求直线方程的方法是通法,必须掌握;
②解法二是常常采用的解题技巧。
