江苏省启东市2019-2020学年高一下学期期末调研测试数学试题 图片版含答案
文档属性
| 名称 | 江苏省启东市2019-2020学年高一下学期期末调研测试数学试题 图片版含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 21.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-18 00:00:00 | ||
图片预览



文档简介
数学参考答案与评分建议
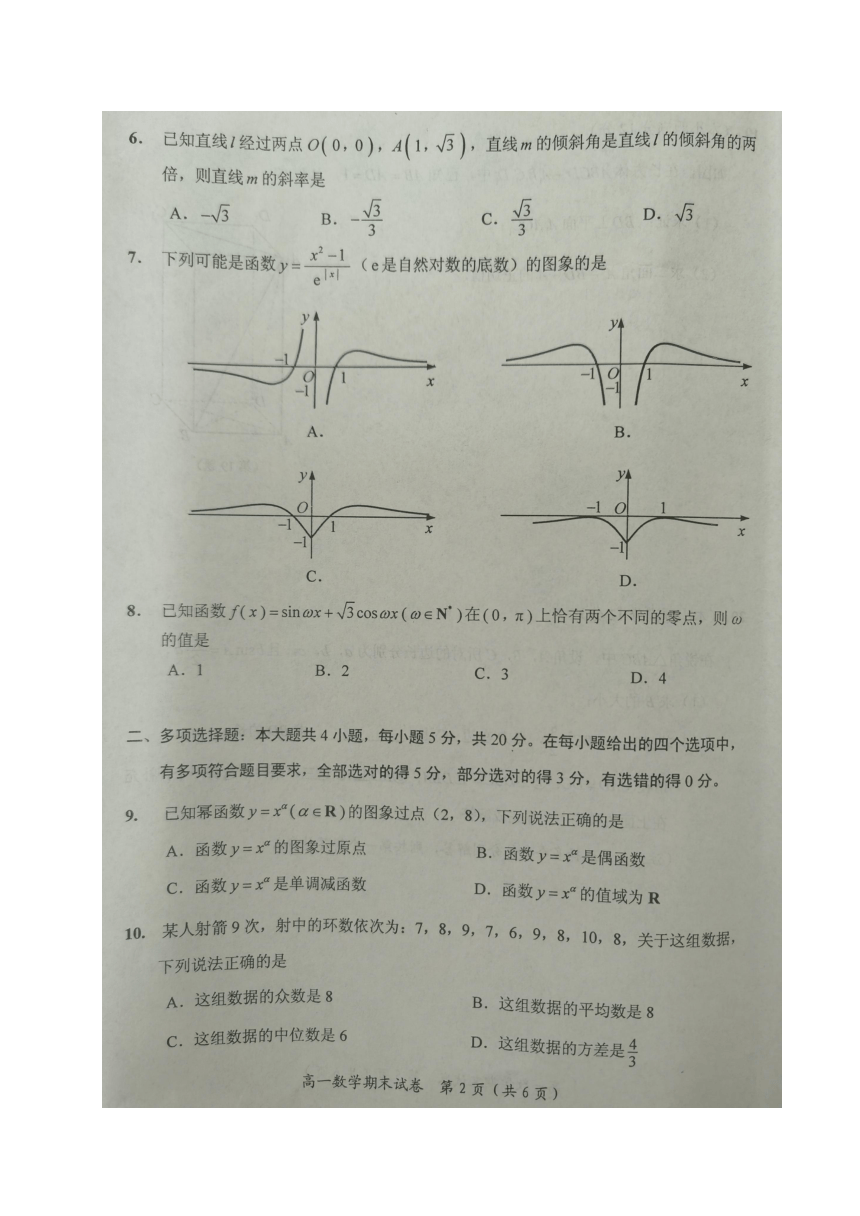
一、单项选择题:本题共8小题,每小题5分,共40分。
1~4 C C D B 5~8 B A C B
二、多项选择题:本题共4小题,每小题5分,共20分。
9. AD 10. ABD 11. AC 12. ABC
三、填空题:本题共4小题,每小题5分,共20分。
13. 式子的值是 ▲ .
【答案】6
14.已知,α为锐角,则 ▲ .
【答案】
15.已知直线与圆相切,则a的值是 ▲ .
【答案】1
16.“辛普森(Simpson)公式”给出了求几何体体积的一种估算方法:几何体的体积等于其
上底的面积S、中截面(过几何体高的中点平行于底面的截面)的面积S0的4倍、下底的面积之和乘以高h的六分之一,即.已知函数的图象过点,,且与直线,y1及y2围成的封闭图形绕y轴旋转一周得到一个几何体,则 ▲ ,利用“辛普森(Simpson)公式”可估算该几何体的体积 ▲ .(第一空2分,第二空3分)
【答案】1,
四、解答题:本大题共6小题,共计70分.
17. (本小题满分10分)
已知,,与的夹角为.
求:(1);
(2).
解:(1) ……2分
. ……5分
(2)
……7分
. ……10分
18. (本小题满分12分)
眼睛是心灵的窗户,保护好视力非常重要.某校高一、高二、高三年级分别有学生1 200名、
1 080名、720名.为了解全校学生的视力情况,学校在6月6日“全国爱眼日”采用分层抽样的方法,抽取50人测试视力,并根据测试数据绘制了如图所示的频率分布直方图.
(1)求从高一年级抽取的学生人数;
??????(2)试估计该学校学生视力不低于4.8的概率;
(3)从视力在内的受测者中随机抽取
2人,求2人视力都在内的概率.
解:(1)高一年级抽取的学生人数为:
.
答:从高一年级抽取的学生人数为20. ……2分
?? (2)由频率分布直方图,得,
所以. ……4分
所以抽取50名学生中,视力不低于4.8的频率为,
所以该校学生视力不低于4.8的概率的估计值为. ……6分
(3)由频率分布直方图,得
视力在内的受测者人数为,记这2人为,
视力在内的受测者人数为,记这3人为.……8分
记“抽取2人视力都在内”为事件A,
从视力在内的受测者中随机抽取2人,所有的等可能基本事件共有10个,
分别为
,
则事件A包含其中3个基本事件:, ……10分
根据古典概型的概率公式,得.
答:2人视力都在内的概率为. ……12分
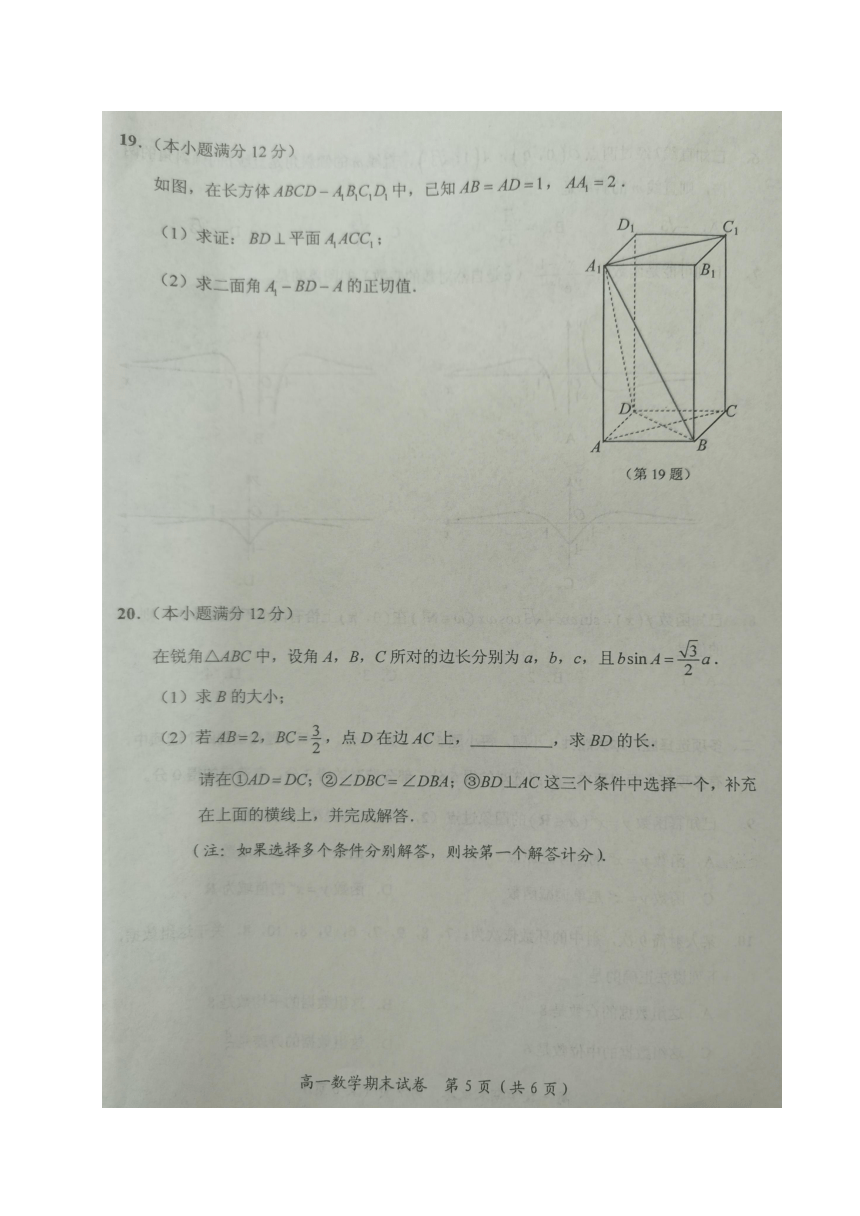
19.(本小题满分12分)
如图,在长方体中,已知,.
(1)求证:平面;
(2)求二面角的正切值.
解:(1)因为为长方体,
所以平面.
因为平面,所以. ……2分
因为,所以为正方形.
所以. ……4分
又因为,平面,
所以平面. ……6分
?? (2)设,连接.
由(1)知,平面.
因为平面,所以. ……8分
又由(1)知,,
所以为二面角的平面角. ……10分
在中,,,
所以,
所以二面角的正切值为. ……12分
20.(本小题满分12分)
在锐角△ABC中,设角A,B,C所对的边长分别为a,b,c,且.
(1)求B的大小;
(2)若AB2,BC,点D在边AC上, ,求BD的长.
请在①ADDC;②∠DBC∠DBA;③BD⊥AC这三个条件中选择一个,补充在上面
的横线上,并完成解答.
(注:如果选择多个条件分别解答,则按第一个解答计分).
解:(1)在△ABC中,由正弦定理,及得,
. ……2分
因为△ABC为锐角三角形,所以,所以.
所以. ……4分
又因为,所以. ……6分
(2)若选①.
法一:在△ABC中,因为ADDC,所以=. ……8分
所以2 ……10分
所以BD=. ……12分
法二:在△ABC中,由余弦定理,得
,
所以,所以. ……8分
在△ABD中,由余弦定理,得
即,
在△BDC中,由余弦定理,得
即. ……10分
又,所以.
所以,
所以BD=. ……12分
若选②.
在△ABC中,, ……8分
即, ……10分
即,
解得. ……12分
若选③.
在△ABC中,由余弦定理,得
,
所以. ……8分
因为,又, ……10分
所以,
解得. ……12分
21.(本小题满分12分)
已知圆C:关于直线l:对称.
(1)求实数a的值;
(2)设直线m:与圆交于点,且.
① 求的值;
② 点P ( 3,0 ),证明:x轴平分.
解:(1)因为圆C:关于直线l:对称,
所以圆心C在直线l:上. ……2分
所以,解得. ……4分
?? (2)① 由(1)知,圆C:.
所以圆心C到直线m:的距离为. ……6分
因为,所以,解得,
因为,所以. ……8分
② 法一:由①知,直线m:.
联立消去,得,解得或.
不妨, ……10分
所以.
所以直线的倾斜角互补,从而,
所以轴平分. ……12分
法二:设直线m:上的点,,又点P ( 3,0 ),
所以
.(*) ……8分
联立消去,得,
所以 代入(*),得.
所以直线的倾斜角互补,从而,
所以轴平分. ……12分
22.(本小题满分12分)
已知函数分别是定义在上的偶函数和奇函数,且.
(1)求函数与的解析式;
(2)设函数,若对任意实数,恒成立,求实数
的取值范围.
解:(1)因为为偶函数,为奇函数,且,①
所以,即, ② ……2分
由,得,
由,得. ……4分
(2)方法一:由(1)得,.
因为对任意实数,恒成立.
当时,设,则恒成立.
若,即,则当时,取得最小值,符合题意; ……6分
若,即,则当时,取得最小值.
由,得,所以.
所以. ……8分
当时,设,则恒成立.
若,即,则当时,取得最小值.
由,得. 所以. ……10分
若,即时,,符合题意.
所以.
综上,实数的取值范围是. ……12分
方法二:恒成立,即恒成立.
当时,显然成立;
当时,,令,设, ……6分
当,即时,.
设是上任意两个值,且,
则,
当时,,,,所以,即;
当时,,,,所以,即,
所以函数在上单调递增,在上单调递减. ……8分
所以当时,在上取得最大值.
所以. ……10分
当,即时,,
同理可证,函数在 上单调递增,在上单调递减.
所以当时,在上取得最大值.
所以.
综上,实数的取值范围是. ……12分
一、单项选择题:本题共8小题,每小题5分,共40分。
1~4 C C D B 5~8 B A C B
二、多项选择题:本题共4小题,每小题5分,共20分。
9. AD 10. ABD 11. AC 12. ABC
三、填空题:本题共4小题,每小题5分,共20分。
13. 式子的值是 ▲ .
【答案】6
14.已知,α为锐角,则 ▲ .
【答案】
15.已知直线与圆相切,则a的值是 ▲ .
【答案】1
16.“辛普森(Simpson)公式”给出了求几何体体积的一种估算方法:几何体的体积等于其
上底的面积S、中截面(过几何体高的中点平行于底面的截面)的面积S0的4倍、下底的面积之和乘以高h的六分之一,即.已知函数的图象过点,,且与直线,y1及y2围成的封闭图形绕y轴旋转一周得到一个几何体,则 ▲ ,利用“辛普森(Simpson)公式”可估算该几何体的体积 ▲ .(第一空2分,第二空3分)
【答案】1,
四、解答题:本大题共6小题,共计70分.
17. (本小题满分10分)
已知,,与的夹角为.
求:(1);
(2).
解:(1) ……2分
. ……5分
(2)
……7分
. ……10分
18. (本小题满分12分)
眼睛是心灵的窗户,保护好视力非常重要.某校高一、高二、高三年级分别有学生1 200名、
1 080名、720名.为了解全校学生的视力情况,学校在6月6日“全国爱眼日”采用分层抽样的方法,抽取50人测试视力,并根据测试数据绘制了如图所示的频率分布直方图.
(1)求从高一年级抽取的学生人数;
??????(2)试估计该学校学生视力不低于4.8的概率;
(3)从视力在内的受测者中随机抽取
2人,求2人视力都在内的概率.
解:(1)高一年级抽取的学生人数为:
.
答:从高一年级抽取的学生人数为20. ……2分
?? (2)由频率分布直方图,得,
所以. ……4分
所以抽取50名学生中,视力不低于4.8的频率为,
所以该校学生视力不低于4.8的概率的估计值为. ……6分
(3)由频率分布直方图,得
视力在内的受测者人数为,记这2人为,
视力在内的受测者人数为,记这3人为.……8分
记“抽取2人视力都在内”为事件A,
从视力在内的受测者中随机抽取2人,所有的等可能基本事件共有10个,
分别为
,
则事件A包含其中3个基本事件:, ……10分
根据古典概型的概率公式,得.
答:2人视力都在内的概率为. ……12分
19.(本小题满分12分)
如图,在长方体中,已知,.
(1)求证:平面;
(2)求二面角的正切值.
解:(1)因为为长方体,
所以平面.
因为平面,所以. ……2分
因为,所以为正方形.
所以. ……4分
又因为,平面,
所以平面. ……6分
?? (2)设,连接.
由(1)知,平面.
因为平面,所以. ……8分
又由(1)知,,
所以为二面角的平面角. ……10分
在中,,,
所以,
所以二面角的正切值为. ……12分
20.(本小题满分12分)
在锐角△ABC中,设角A,B,C所对的边长分别为a,b,c,且.
(1)求B的大小;
(2)若AB2,BC,点D在边AC上, ,求BD的长.
请在①ADDC;②∠DBC∠DBA;③BD⊥AC这三个条件中选择一个,补充在上面
的横线上,并完成解答.
(注:如果选择多个条件分别解答,则按第一个解答计分).
解:(1)在△ABC中,由正弦定理,及得,
. ……2分
因为△ABC为锐角三角形,所以,所以.
所以. ……4分
又因为,所以. ……6分
(2)若选①.
法一:在△ABC中,因为ADDC,所以=. ……8分
所以2 ……10分
所以BD=. ……12分
法二:在△ABC中,由余弦定理,得
,
所以,所以. ……8分
在△ABD中,由余弦定理,得
即,
在△BDC中,由余弦定理,得
即. ……10分
又,所以.
所以,
所以BD=. ……12分
若选②.
在△ABC中,, ……8分
即, ……10分
即,
解得. ……12分
若选③.
在△ABC中,由余弦定理,得
,
所以. ……8分
因为,又, ……10分
所以,
解得. ……12分
21.(本小题满分12分)
已知圆C:关于直线l:对称.
(1)求实数a的值;
(2)设直线m:与圆交于点,且.
① 求的值;
② 点P ( 3,0 ),证明:x轴平分.
解:(1)因为圆C:关于直线l:对称,
所以圆心C在直线l:上. ……2分
所以,解得. ……4分
?? (2)① 由(1)知,圆C:.
所以圆心C到直线m:的距离为. ……6分
因为,所以,解得,
因为,所以. ……8分
② 法一:由①知,直线m:.
联立消去,得,解得或.
不妨, ……10分
所以.
所以直线的倾斜角互补,从而,
所以轴平分. ……12分
法二:设直线m:上的点,,又点P ( 3,0 ),
所以
.(*) ……8分
联立消去,得,
所以 代入(*),得.
所以直线的倾斜角互补,从而,
所以轴平分. ……12分
22.(本小题满分12分)
已知函数分别是定义在上的偶函数和奇函数,且.
(1)求函数与的解析式;
(2)设函数,若对任意实数,恒成立,求实数
的取值范围.
解:(1)因为为偶函数,为奇函数,且,①
所以,即, ② ……2分
由,得,
由,得. ……4分
(2)方法一:由(1)得,.
因为对任意实数,恒成立.
当时,设,则恒成立.
若,即,则当时,取得最小值,符合题意; ……6分
若,即,则当时,取得最小值.
由,得,所以.
所以. ……8分
当时,设,则恒成立.
若,即,则当时,取得最小值.
由,得. 所以. ……10分
若,即时,,符合题意.
所以.
综上,实数的取值范围是. ……12分
方法二:恒成立,即恒成立.
当时,显然成立;
当时,,令,设, ……6分
当,即时,.
设是上任意两个值,且,
则,
当时,,,,所以,即;
当时,,,,所以,即,
所以函数在上单调递增,在上单调递减. ……8分
所以当时,在上取得最大值.
所以. ……10分
当,即时,,
同理可证,函数在 上单调递增,在上单调递减.
所以当时,在上取得最大值.
所以.
综上,实数的取值范围是. ……12分
同课章节目录
