江门市艺华高中2019-2020学年高中物理粤教版选修3-5:1.1物体的碰撞 质量检测(含解析)
文档属性
| 名称 | 江门市艺华高中2019-2020学年高中物理粤教版选修3-5:1.1物体的碰撞 质量检测(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 650.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-07-19 05:31:28 | ||
图片预览




文档简介
1.1物体的碰撞
1.水平面上,一白球与一静止的灰球碰撞,两球质量相等.碰撞过程的频闪照片如图所示,据此可推断,碰撞过程中系统损失的动能约占碰撞前动能的
A.30% B.50% C.70% D.90%
2.质量分别为m1、m2的小球在一直线上发生弹性碰撞,它们在碰撞前后的位移—时间图象如图所示,若m1=1 kg,m2的质量等于( )
A.1 kg B.3 kg
C.5 kg D.10 kg
3.某人在一只静止的小车上练习打靶,已知车,人,枪(不包括子弹)及靶的总质量为M,枪内装有n颗子弹,每颗子弹的质量均为m,枪口到靶的距离为L,子弹水平射出枪口相对于地面的速度为v,在发射后一颗子弹时,前一颗子弹已嵌入靶中,求发射完n颗子弹时,小车后退的距离为( )
A. B. C. D.
4.如图所示,小车(包括固定在小车上的杆)的质量为M,质量为m的小球通过长度为L的轻绳与杆的顶端连接,开始时小车静止在光滑的水平面上.现把小球从与O点等高的地方释放(小球不会与杆相撞),小车向左运动的最大位移是( )
A. B. C. D.
5.分析下列情况中系统的动量是否守恒 ( )
A.如图2所示,小车停在光滑水平面上,人在车上走动时,对人与车组成的系统
B.子弹射入放在光滑水平面上的木块中对子弹与木块组成的系统(如图3)
C.子弹射入紧靠墙角的木块中,对子弹与木块组成的系统
D.斜向上抛出的手榴弹在空中炸开时
6.如图,两物体A、B用轻质弹簧相连,静止在光滑水平面上,现同时对A、B两物体施加等大反向的水平恒力F1、F2,使A、B同时由静止开始运动,在弹簧由原长伸到最长的过程中,对A、B两物体及弹簧组成的系统,正确的说法是( )
A.A、B先做变加速运动,当F1、F2和弹力相等时,A、B的速度最大;之后,A、B做变减速运动,直至速度减到零
B.A、B做变减速运动速度减为零时,弹簧伸长最长,系统的机械能最大
C.A、B、弹簧组成的系统机械能在这一过程中是先增大后减小
D.因F1、F2等值反向,故A、B、弹簧组成的系统的动量守恒
7.如图所示,在粗糙水平面上,用水平轻绳连接的两个材料相同的物体A、B,质量均为m在水平恒力的作用下以速度v做匀速运动,在t=0时轻绳断开,在F作用下继续前进,则下列说法正确的是( )
A.至时间内,A、B的总动量守恒
B.时,A的动量为2mv
C. 至时间内,A、 B的总动量不守恒
D.时,A的动量为2mv
8.如图所示,现有甲、乙两滑块,质量分别为3m和m,以相同的速率v在光滑水平面上相向运动,发生碰撞.已知碰撞后,甲滑块静止不动,则
A.碰撞前总动量大小为2mv
B.碰撞过程动量不守恒
C.碰撞后乙的速度大小为2v
D.碰撞属于非弹性碰撞
9.A、B两球沿一直线运动并发生正碰,如图为两球碰撞前后的位移与时间图像,a、b分别为A、B两球碰前的位移与时间图像,c为碰撞后两球共同运动的位移与时间图像,若A球质量是m=2 kg,则由图判断下列结论正确的是( )
A.碰撞前后A的动量变化为4 kg·m/s
B.碰撞时A对B所施冲量为-4 N·s
C.A、B碰撞前的总动量为3 kg·m/s
D.碰撞中A、B两球组成的系统损失的动能为10 J
10.如图所示,光滑水平面上有大小相同的A、B两球在同一直线上运动.两球质量关系为,规定向右为正方向,A、B两球的动量均为,运动中两球发生碰撞,碰撞后A球的动量增量为,则( )
A.该碰撞为弹性碰撞
B.该碰撞为非弹性碰撞
C.左方是A球,碰撞后A、B两球速度大小之比为2:5
D.右方是A球,碰撞后A、B两球速度大小之比为1∶10
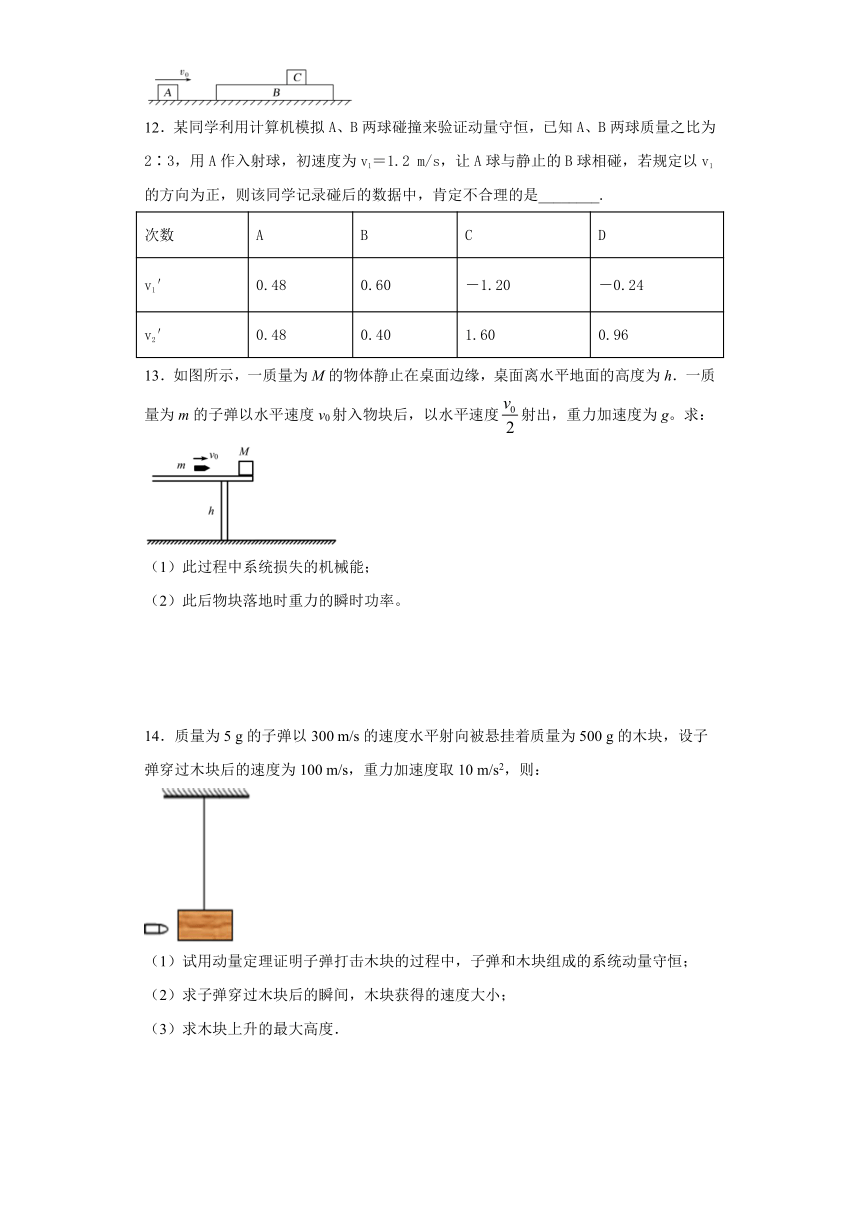
11.如图所示,木块A的质量mA=1kg,足够长的木板B的质量mB=4kg,质量为mC=4kg的木块C置于木板B上,水平面光滑,B、C之间有摩擦。现使A以v0=12m/s的初速度向右运动,与B碰撞后以4m/s的速度弹回,则A与B碰撞后瞬间,B的速度为__m/s ,C运动过程中的最大速度为__m/s ,整个过程中因为B、C之间的摩擦而产生的总内能为___J。
12.某同学利用计算机模拟A、B两球碰撞来验证动量守恒,已知A、B两球质量之比为2∶3,用A作入射球,初速度为v1=1.2 m/s,让A球与静止的B球相碰,若规定以v1的方向为正,则该同学记录碰后的数据中,肯定不合理的是________.
次数 A B C D
v1′ 0.48 0.60 -1.20 -0.24
v2′ 0.48 0.40 1.60 0.96
13.如图所示,一质量为M的物体静止在桌面边缘,桌面离水平地面的高度为h.一质量为m的子弹以水平速度v0射入物块后,以水平速度射出,重力加速度为g。求:
(1)此过程中系统损失的机械能;
(2)此后物块落地时重力的瞬时功率。
14.质量为5 g的子弹以300 m/s的速度水平射向被悬挂着质量为500 g的木块,设子弹穿过木块后的速度为100 m/s,重力加速度取10 m/s2,则:
(1)试用动量定理证明子弹打击木块的过程中,子弹和木块组成的系统动量守恒;
(2)求子弹穿过木块后的瞬间,木块获得的速度大小;
(3)求木块上升的最大高度.
参考答案
1.A
【解析】
由题图可以判断,碰撞前白球、碰撞后白球与灰球均做匀速直线运动,碰后两球速度大小相等,设为v,碰前白球的速度约为碰后速度的1.7倍,即1.7v,碰前系统的动能Ek1=m·(1.7v)2,碰后系统的动能Ek2=2×mv2,碰撞过程中系统损失的动能约占碰撞前动能为≈31%,选项A正确.
2.B
【解析】
碰撞前m2是静止的,m1的速度为:
碰后m1的速度:
m2的速度:
根据动量守恒定律有:
m1v1=m1v1′+m2v2′
代入得:
1×4=1×(-2)+m2×2
解得:
m2=3kg
A.1 kg,与结论不相符,选项A错误;
B.3 kg,与结论相符,选项B正确;
C.5 kg,与结论不相符,选项C错误;
D.10 kg,与结论不相符,选项D错误;
3.C
【解析】
以船、人连同枪(不包括子弹)、靶以及枪内有n颗子弹组成的系统为研究的对象,取子弹的速度方向为正方向。当射出一粒子弹时,由系统的动量守恒得:
mv-[M+(n-1)m]v′=0
设每颗子弹经过时间t打到靶上,则有:
vt+v′t=L
联立以上两式得:
同理射完n颗子弹的过程中,每一次发射子弹船后推的距离都相同,所以船后退的总距离为:
。
A.,与结论不相符,选项A错误;
B.,与结论不相符,选项B错误;
C.,与结论相符,选项C正确;
D.,与结论不相符,选项D错误;
4.B
【解析】
分析可知小球在下摆过程中,小车向左加速,当小球从最低点向上摆动过程中,小车向左减速,当小球摆到右边且与O点等高时,小车的速度减为零,此时小车向左的位移达到最大,小球相对于小车的位移为2L.小球和小车组成的系统在水平方向上动量守恒,设小球和小车在水平方向上的速度大小分别为v1、v2,有
mv1=Mv2
故
ms1=Ms2
s1+s2=2L
其中s1代表小球的水平位移大小,s2代表小车的水平位移大小,因此
s2=
A. ,与结论不相符,选项A错误;
B. ,与结论相符,选项B正确;
C. ,与结论不相符,选项C错误;
D. ,与结论不相符,选项D错误。
5.ABD
【解析】
系统所受外力为零、碰撞过程动量守恒,选项C中子弹与木块组成的系统水平方向要受到墙面的弹力作用,动量不守恒,C错;
6.ABD
【解析】
A.在拉力作用下,A、B开始做如速运动。弹簧伸长,弹簧弹力变大,物体A、B受到的合力变小,物体加速度变小,物体做加速度减小的加速运动,当弹簧弹力等于拉力时物体受到的合力为零,速度达到最大,之后弹簧弹力大于拉力,两物体减速运动,直到速度为零时,弹簧伸长量达最大,因此A、B先做变加速运动,当F1、F2和弹力相等时,A、B的速度最大;之后,A、B做变减速运动,直至速度减到零,故A符合题意;
BC.在整个过程中,拉力一直对系统做正功,系统机械能增加,A、B做变减速运动速度减为零时,弹簧伸长最长,系统的机械能最大,故B符合题意,C不符合题意;
D.因F1、F2等大反向,故A、B、弹簧组成的系统所受合外力为零,系统动量守恒,故D符合题意。
7.ABC
【解析】
A.在B停止滑动前,以整体为研究对象,A、B摩擦力并没有发生变化,所以AB的合外力仍为零,所以系统动量守恒,A、B所受摩擦力均为,所以从t=0到B停下,对B,由动量定理得:
即:时,B停下。所以t=0至时间内,A、B的总动量守恒,故A正确;
BD.时,即B刚停下时,对AB,从t=0到,以向右为正方向,由动量守恒定律得:
2mv=P′+0
解得A的动量为:
P′=2mv
即 时,A的动量等于2mv;时,A的动量大于2mv,故B正确,D错误;
C.至时间内,B已经停止运动,A合外力不为零,所以A、B的总动量不守恒,故C正确;
8.AC
【解析】
A.取向右为正方向,碰撞前总动量为3mv-mv=2mv,A正确;
B.碰撞过程两滑块组成的系统在水平方向不受外力,则系统动量守恒,B错误;
C.设碰撞后乙的速度为v′,由动量守恒定律得
3mv-mv=0+mv′,
解得
v′=2v,
C正确;
D.碰撞前总动能为·3mv2+mv2=2mv2,碰撞后总动能为0+m(2v)2=2mv2,碰撞前后无机械能损失,碰撞属于弹性碰撞,D错误.
9.ABD
【解析】
A项:由x-t图象的斜率表示速度,可知,碰撞前有:
碰撞后有:
,则碰撞前后A的动量变化为:
,故A正确;
B项:对A、B组成的系统,根据动量守恒定律知:碰撞前后B的动量变化为:,对B,由动量定理可知,碰撞时A对B所施冲量为:,故B正确;
C项:由,所以:,则A与B碰撞前的总动量为:,故C错误;
D项:碰撞中A、B两球组成的系统损失的动能:,代入数据解得,故D正确。
10.AC
【解析】规定向右为正方向,碰撞前A、B两球的动量均为6kg?m/s,说明A、B两球的速度方向向右,两球质量关系为mB=2mA,所以碰撞前vA>vB,所以左方是A球.碰撞后A球的动量增量为-4kg?m/s,所以碰撞后A球的动量是2kg?m/s;碰撞过程系统总动量守恒:mAvA+mBvB=-mAvA′+mBvB′所以碰撞后B球的动量是10kg?m/s,根据mB=2mA,所以碰撞后A、B两球速度大小之比为2:5,故C正确,D错误.碰撞前系统动能:,碰撞后系统动能为:,则碰撞前后系统机械能不变,碰撞是弹性碰撞,故A正确,B错误;故选AC.
点睛:碰撞过程中动量守恒,同时要遵循能量守恒定律,不忘联系实际情况,即后面的球不会比前面的球运动的快;由于动量是矢量,具有方向性,在讨论动量守恒时必须注意到其方向性.为此首先规定一个正方向,然后在此基础上进行研究.
11.4 2 16
【解析】
[1]A与B碰瞬间,C的运动状态未变,B速度最大。以A、B组成的系统为研究对象,以A的初速度方向为正方向,由动量守恒定律得
mAv0=-mAvA+mBvB,
代入数据得A与B碰撞后瞬间,B的速度vB=4m/s。
[2]A、B碰撞后,B与C相互作用使B减速、C加速,由于B板足够长,所以B和C能达到相同速度,二者共速后,C速度最大,以B、C组成的系统为研究对象,以向右为正方向,由动量守恒定律
mBvB=(mB+mC)vC
代入数据得C运动过程中的最大速度vC=2m/s.
[3]整个过程中因为B、C之间的摩擦而产生的总内能E=mBvB2-(mB+mC)vC2=16J。
12.BC
【解析】
设两球的质量分别为2m、3m;则碰前总动量2.4m;碰前总动能;
对选项A,碰后动量:(2m+3m)×0.48=2.4m,则动量守恒,末状态总动能,则A项合理;B项中碰后A球速度不可能大于B球速度,则B不合理;同理C项中动量2m×(-1.2)+3m×1.6=2.4m,动量守恒,末状态总动能,则C项不合理;D项中动量2m×(-0.24)+3m×0.96=2.4m,动量守恒守恒,末状态总动能,合理.题目中要求选不合理的,故选BC.
点睛:对于碰撞过程要遵守三大规律:1、是动量守恒定律;2、总动能不增加;3、符合物体的实际运动情况.
13.(1) ; (2)
【解析】
(1)子弹射出的过程:
得:
(2)物体落地时竖直方向满足:
解得:
重力的瞬时功率:
14.(1)+ Mv2=mv0 (2) v2=2m/s (3) h=0.2m
【解析】
由题中“子弹穿过木块”可知,本题考查动量定理和机械能守恒,根据过程分析运用动量定理公式和机械能守恒定律进行解题。
【详解】
(1)设子弹质量为m,打击木块前的速度为v0,穿出后的速度为v1,木块质量为M,获得的速度为v2,打击过程中,木块受到的平均作用力为F,时间为t.以子弹的初速度v0的方向为正方向.
对子弹应用动量定理
对木块应用动量定理
上面两式相加有
即:
子弹和木块组成的系统动量守恒.
(2)由动量守恒定律
解得v2=2m/s
(3)由机械能守恒有
解得h=0.2m
1.水平面上,一白球与一静止的灰球碰撞,两球质量相等.碰撞过程的频闪照片如图所示,据此可推断,碰撞过程中系统损失的动能约占碰撞前动能的
A.30% B.50% C.70% D.90%
2.质量分别为m1、m2的小球在一直线上发生弹性碰撞,它们在碰撞前后的位移—时间图象如图所示,若m1=1 kg,m2的质量等于( )
A.1 kg B.3 kg
C.5 kg D.10 kg
3.某人在一只静止的小车上练习打靶,已知车,人,枪(不包括子弹)及靶的总质量为M,枪内装有n颗子弹,每颗子弹的质量均为m,枪口到靶的距离为L,子弹水平射出枪口相对于地面的速度为v,在发射后一颗子弹时,前一颗子弹已嵌入靶中,求发射完n颗子弹时,小车后退的距离为( )
A. B. C. D.
4.如图所示,小车(包括固定在小车上的杆)的质量为M,质量为m的小球通过长度为L的轻绳与杆的顶端连接,开始时小车静止在光滑的水平面上.现把小球从与O点等高的地方释放(小球不会与杆相撞),小车向左运动的最大位移是( )
A. B. C. D.
5.分析下列情况中系统的动量是否守恒 ( )
A.如图2所示,小车停在光滑水平面上,人在车上走动时,对人与车组成的系统
B.子弹射入放在光滑水平面上的木块中对子弹与木块组成的系统(如图3)
C.子弹射入紧靠墙角的木块中,对子弹与木块组成的系统
D.斜向上抛出的手榴弹在空中炸开时
6.如图,两物体A、B用轻质弹簧相连,静止在光滑水平面上,现同时对A、B两物体施加等大反向的水平恒力F1、F2,使A、B同时由静止开始运动,在弹簧由原长伸到最长的过程中,对A、B两物体及弹簧组成的系统,正确的说法是( )
A.A、B先做变加速运动,当F1、F2和弹力相等时,A、B的速度最大;之后,A、B做变减速运动,直至速度减到零
B.A、B做变减速运动速度减为零时,弹簧伸长最长,系统的机械能最大
C.A、B、弹簧组成的系统机械能在这一过程中是先增大后减小
D.因F1、F2等值反向,故A、B、弹簧组成的系统的动量守恒
7.如图所示,在粗糙水平面上,用水平轻绳连接的两个材料相同的物体A、B,质量均为m在水平恒力的作用下以速度v做匀速运动,在t=0时轻绳断开,在F作用下继续前进,则下列说法正确的是( )
A.至时间内,A、B的总动量守恒
B.时,A的动量为2mv
C. 至时间内,A、 B的总动量不守恒
D.时,A的动量为2mv
8.如图所示,现有甲、乙两滑块,质量分别为3m和m,以相同的速率v在光滑水平面上相向运动,发生碰撞.已知碰撞后,甲滑块静止不动,则
A.碰撞前总动量大小为2mv
B.碰撞过程动量不守恒
C.碰撞后乙的速度大小为2v
D.碰撞属于非弹性碰撞
9.A、B两球沿一直线运动并发生正碰,如图为两球碰撞前后的位移与时间图像,a、b分别为A、B两球碰前的位移与时间图像,c为碰撞后两球共同运动的位移与时间图像,若A球质量是m=2 kg,则由图判断下列结论正确的是( )
A.碰撞前后A的动量变化为4 kg·m/s
B.碰撞时A对B所施冲量为-4 N·s
C.A、B碰撞前的总动量为3 kg·m/s
D.碰撞中A、B两球组成的系统损失的动能为10 J
10.如图所示,光滑水平面上有大小相同的A、B两球在同一直线上运动.两球质量关系为,规定向右为正方向,A、B两球的动量均为,运动中两球发生碰撞,碰撞后A球的动量增量为,则( )
A.该碰撞为弹性碰撞
B.该碰撞为非弹性碰撞
C.左方是A球,碰撞后A、B两球速度大小之比为2:5
D.右方是A球,碰撞后A、B两球速度大小之比为1∶10
11.如图所示,木块A的质量mA=1kg,足够长的木板B的质量mB=4kg,质量为mC=4kg的木块C置于木板B上,水平面光滑,B、C之间有摩擦。现使A以v0=12m/s的初速度向右运动,与B碰撞后以4m/s的速度弹回,则A与B碰撞后瞬间,B的速度为__m/s ,C运动过程中的最大速度为__m/s ,整个过程中因为B、C之间的摩擦而产生的总内能为___J。
12.某同学利用计算机模拟A、B两球碰撞来验证动量守恒,已知A、B两球质量之比为2∶3,用A作入射球,初速度为v1=1.2 m/s,让A球与静止的B球相碰,若规定以v1的方向为正,则该同学记录碰后的数据中,肯定不合理的是________.
次数 A B C D
v1′ 0.48 0.60 -1.20 -0.24
v2′ 0.48 0.40 1.60 0.96
13.如图所示,一质量为M的物体静止在桌面边缘,桌面离水平地面的高度为h.一质量为m的子弹以水平速度v0射入物块后,以水平速度射出,重力加速度为g。求:
(1)此过程中系统损失的机械能;
(2)此后物块落地时重力的瞬时功率。
14.质量为5 g的子弹以300 m/s的速度水平射向被悬挂着质量为500 g的木块,设子弹穿过木块后的速度为100 m/s,重力加速度取10 m/s2,则:
(1)试用动量定理证明子弹打击木块的过程中,子弹和木块组成的系统动量守恒;
(2)求子弹穿过木块后的瞬间,木块获得的速度大小;
(3)求木块上升的最大高度.
参考答案
1.A
【解析】
由题图可以判断,碰撞前白球、碰撞后白球与灰球均做匀速直线运动,碰后两球速度大小相等,设为v,碰前白球的速度约为碰后速度的1.7倍,即1.7v,碰前系统的动能Ek1=m·(1.7v)2,碰后系统的动能Ek2=2×mv2,碰撞过程中系统损失的动能约占碰撞前动能为≈31%,选项A正确.
2.B
【解析】
碰撞前m2是静止的,m1的速度为:
碰后m1的速度:
m2的速度:
根据动量守恒定律有:
m1v1=m1v1′+m2v2′
代入得:
1×4=1×(-2)+m2×2
解得:
m2=3kg
A.1 kg,与结论不相符,选项A错误;
B.3 kg,与结论相符,选项B正确;
C.5 kg,与结论不相符,选项C错误;
D.10 kg,与结论不相符,选项D错误;
3.C
【解析】
以船、人连同枪(不包括子弹)、靶以及枪内有n颗子弹组成的系统为研究的对象,取子弹的速度方向为正方向。当射出一粒子弹时,由系统的动量守恒得:
mv-[M+(n-1)m]v′=0
设每颗子弹经过时间t打到靶上,则有:
vt+v′t=L
联立以上两式得:
同理射完n颗子弹的过程中,每一次发射子弹船后推的距离都相同,所以船后退的总距离为:
。
A.,与结论不相符,选项A错误;
B.,与结论不相符,选项B错误;
C.,与结论相符,选项C正确;
D.,与结论不相符,选项D错误;
4.B
【解析】
分析可知小球在下摆过程中,小车向左加速,当小球从最低点向上摆动过程中,小车向左减速,当小球摆到右边且与O点等高时,小车的速度减为零,此时小车向左的位移达到最大,小球相对于小车的位移为2L.小球和小车组成的系统在水平方向上动量守恒,设小球和小车在水平方向上的速度大小分别为v1、v2,有
mv1=Mv2
故
ms1=Ms2
s1+s2=2L
其中s1代表小球的水平位移大小,s2代表小车的水平位移大小,因此
s2=
A. ,与结论不相符,选项A错误;
B. ,与结论相符,选项B正确;
C. ,与结论不相符,选项C错误;
D. ,与结论不相符,选项D错误。
5.ABD
【解析】
系统所受外力为零、碰撞过程动量守恒,选项C中子弹与木块组成的系统水平方向要受到墙面的弹力作用,动量不守恒,C错;
6.ABD
【解析】
A.在拉力作用下,A、B开始做如速运动。弹簧伸长,弹簧弹力变大,物体A、B受到的合力变小,物体加速度变小,物体做加速度减小的加速运动,当弹簧弹力等于拉力时物体受到的合力为零,速度达到最大,之后弹簧弹力大于拉力,两物体减速运动,直到速度为零时,弹簧伸长量达最大,因此A、B先做变加速运动,当F1、F2和弹力相等时,A、B的速度最大;之后,A、B做变减速运动,直至速度减到零,故A符合题意;
BC.在整个过程中,拉力一直对系统做正功,系统机械能增加,A、B做变减速运动速度减为零时,弹簧伸长最长,系统的机械能最大,故B符合题意,C不符合题意;
D.因F1、F2等大反向,故A、B、弹簧组成的系统所受合外力为零,系统动量守恒,故D符合题意。
7.ABC
【解析】
A.在B停止滑动前,以整体为研究对象,A、B摩擦力并没有发生变化,所以AB的合外力仍为零,所以系统动量守恒,A、B所受摩擦力均为,所以从t=0到B停下,对B,由动量定理得:
即:时,B停下。所以t=0至时间内,A、B的总动量守恒,故A正确;
BD.时,即B刚停下时,对AB,从t=0到,以向右为正方向,由动量守恒定律得:
2mv=P′+0
解得A的动量为:
P′=2mv
即 时,A的动量等于2mv;时,A的动量大于2mv,故B正确,D错误;
C.至时间内,B已经停止运动,A合外力不为零,所以A、B的总动量不守恒,故C正确;
8.AC
【解析】
A.取向右为正方向,碰撞前总动量为3mv-mv=2mv,A正确;
B.碰撞过程两滑块组成的系统在水平方向不受外力,则系统动量守恒,B错误;
C.设碰撞后乙的速度为v′,由动量守恒定律得
3mv-mv=0+mv′,
解得
v′=2v,
C正确;
D.碰撞前总动能为·3mv2+mv2=2mv2,碰撞后总动能为0+m(2v)2=2mv2,碰撞前后无机械能损失,碰撞属于弹性碰撞,D错误.
9.ABD
【解析】
A项:由x-t图象的斜率表示速度,可知,碰撞前有:
碰撞后有:
,则碰撞前后A的动量变化为:
,故A正确;
B项:对A、B组成的系统,根据动量守恒定律知:碰撞前后B的动量变化为:,对B,由动量定理可知,碰撞时A对B所施冲量为:,故B正确;
C项:由,所以:,则A与B碰撞前的总动量为:,故C错误;
D项:碰撞中A、B两球组成的系统损失的动能:,代入数据解得,故D正确。
10.AC
【解析】规定向右为正方向,碰撞前A、B两球的动量均为6kg?m/s,说明A、B两球的速度方向向右,两球质量关系为mB=2mA,所以碰撞前vA>vB,所以左方是A球.碰撞后A球的动量增量为-4kg?m/s,所以碰撞后A球的动量是2kg?m/s;碰撞过程系统总动量守恒:mAvA+mBvB=-mAvA′+mBvB′所以碰撞后B球的动量是10kg?m/s,根据mB=2mA,所以碰撞后A、B两球速度大小之比为2:5,故C正确,D错误.碰撞前系统动能:,碰撞后系统动能为:,则碰撞前后系统机械能不变,碰撞是弹性碰撞,故A正确,B错误;故选AC.
点睛:碰撞过程中动量守恒,同时要遵循能量守恒定律,不忘联系实际情况,即后面的球不会比前面的球运动的快;由于动量是矢量,具有方向性,在讨论动量守恒时必须注意到其方向性.为此首先规定一个正方向,然后在此基础上进行研究.
11.4 2 16
【解析】
[1]A与B碰瞬间,C的运动状态未变,B速度最大。以A、B组成的系统为研究对象,以A的初速度方向为正方向,由动量守恒定律得
mAv0=-mAvA+mBvB,
代入数据得A与B碰撞后瞬间,B的速度vB=4m/s。
[2]A、B碰撞后,B与C相互作用使B减速、C加速,由于B板足够长,所以B和C能达到相同速度,二者共速后,C速度最大,以B、C组成的系统为研究对象,以向右为正方向,由动量守恒定律
mBvB=(mB+mC)vC
代入数据得C运动过程中的最大速度vC=2m/s.
[3]整个过程中因为B、C之间的摩擦而产生的总内能E=mBvB2-(mB+mC)vC2=16J。
12.BC
【解析】
设两球的质量分别为2m、3m;则碰前总动量2.4m;碰前总动能;
对选项A,碰后动量:(2m+3m)×0.48=2.4m,则动量守恒,末状态总动能,则A项合理;B项中碰后A球速度不可能大于B球速度,则B不合理;同理C项中动量2m×(-1.2)+3m×1.6=2.4m,动量守恒,末状态总动能,则C项不合理;D项中动量2m×(-0.24)+3m×0.96=2.4m,动量守恒守恒,末状态总动能,合理.题目中要求选不合理的,故选BC.
点睛:对于碰撞过程要遵守三大规律:1、是动量守恒定律;2、总动能不增加;3、符合物体的实际运动情况.
13.(1) ; (2)
【解析】
(1)子弹射出的过程:
得:
(2)物体落地时竖直方向满足:
解得:
重力的瞬时功率:
14.(1)+ Mv2=mv0 (2) v2=2m/s (3) h=0.2m
【解析】
由题中“子弹穿过木块”可知,本题考查动量定理和机械能守恒,根据过程分析运用动量定理公式和机械能守恒定律进行解题。
【详解】
(1)设子弹质量为m,打击木块前的速度为v0,穿出后的速度为v1,木块质量为M,获得的速度为v2,打击过程中,木块受到的平均作用力为F,时间为t.以子弹的初速度v0的方向为正方向.
对子弹应用动量定理
对木块应用动量定理
上面两式相加有
即:
子弹和木块组成的系统动量守恒.
(2)由动量守恒定律
解得v2=2m/s
(3)由机械能守恒有
解得h=0.2m
同课章节目录
