2011年宁波中考复习数学选择题、填空题预测
文档属性
| 名称 | 2011年宁波中考复习数学选择题、填空题预测 | 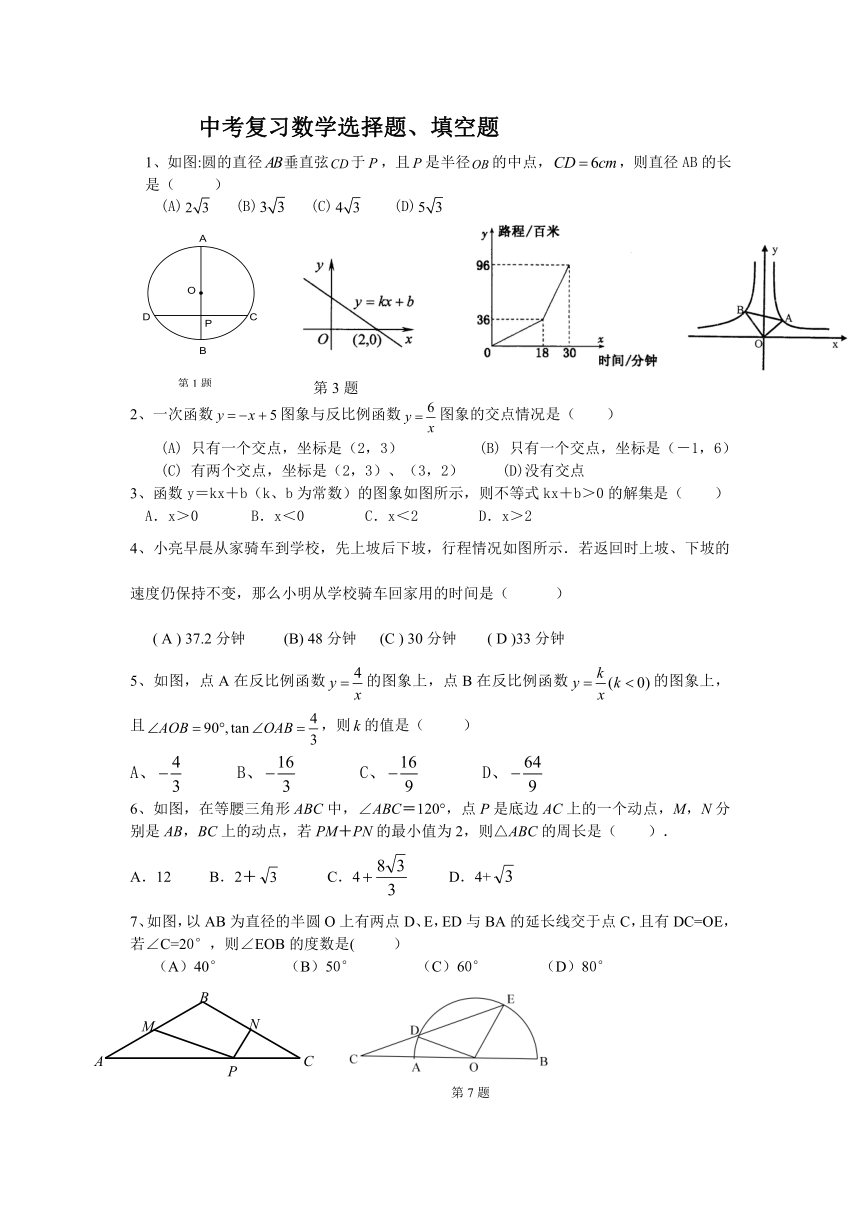 | |
| 格式 | zip | ||
| 文件大小 | 456.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-06-10 11:02:33 | ||
图片预览



文档简介
中考复习数学选择题、填空题
1、如图:圆的直径垂直弦于,且是半径的中点,,则直径AB的长是( )
(A) (B) (C) (D)
第3题
2、一次函数图象与反比例函数图象的交点情况是( )
(A) 只有一个交点,坐标是(2,3) (B) 只有一个交点,坐标是(-1,6)
(C) 有两个交点,坐标是(2,3)、(3,2) (D)没有交点
3、函数y=kx+b(k、b为常数)的图象如图所示,则不等式kx+b>0的解集是( )
A.x>0 B.x<0 C.x<2 D.x>2
4、小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图所示.若返回时上坡、下坡的速度仍保持不变,那么小明从学校骑车回家用的时间是( )
( A ) 37.2分钟 (B) 48分钟 (C ) 30分钟 ( D )33分钟
5、如图,点A在反比例函数的图象上,点B在反比例函数的图象上,且,则的值是( )
A、 B、 C、 D、
6、如图,在等腰三角形ABC中,∠ABC=120°,点P是底边AC上的一个动点,M,N分别是AB,BC上的动点,若PM+PN的最小值为2,则△ABC的周长是( ).
A.12 B.2+ C.4 D.4+
7、如图,以AB为直径的半圆O上有两点D、E,ED与BA的延长线交于点C,且有DC=OE,若∠C=20°,则∠EOB的度数是( )
(A)40° (B)50° (C)60° (D)80°
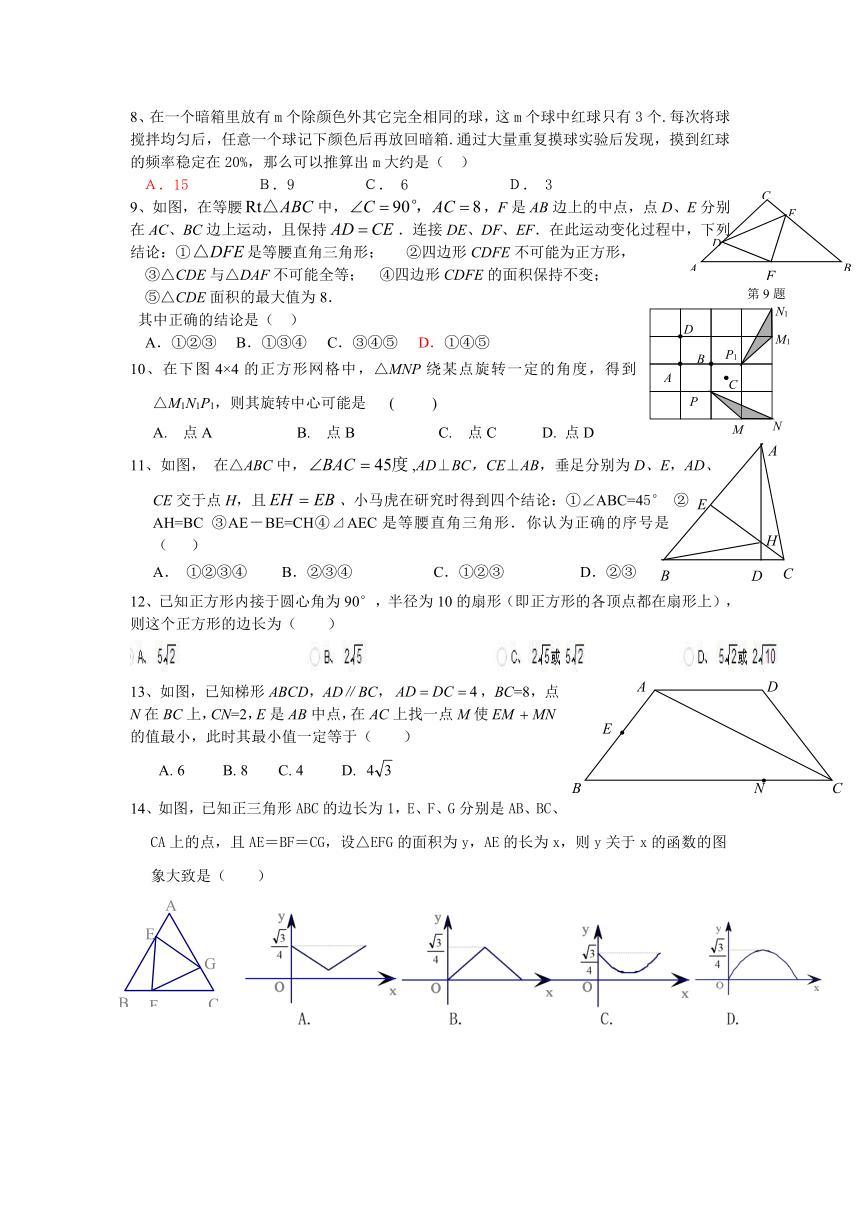
8、在一个暗箱里放有m个除颜色外其它完全相同的球,这m个球中红球只有3个.每次将球搅拌均匀后,任意一个球记下颜色后再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在20%,那么可以推算出m大约是( )
A.15 B.9 C. 6 D. 3
9、如图,在等腰中,,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持.连接DE、DF、EF.在此运动变化过程中,下列结论:①是等腰直角三角形; ②四边形CDFE不可能为正方形,
③△CDE与△DAF不可能全等; ④四边形CDFE的面积保持不变;
⑤△CDE面积的最大值为8.
其中正确的结论是( )
A.①②③ B.①③④ C.③④⑤ D.①④⑤
10、在下图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是 ( )
A. 点A B. 点B C. 点C D. 点D
11、如图, 在△ABC中,,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,且、小马虎在研究时得到四个结论:①∠ABC=45° ②AH=BC ③AE-BE=CH④⊿AEC是等腰直角三角形.你认为正确的序号是( )
A. ①②③④ B.②③④ C.①②③ D.②③
12、已知正方形内接于圆心角为90°,半径为10的扇形(即正方形的各顶点都在扇形上),则这个正方形的边长为( )
13、如图,已知梯形ABCD,AD∥BC,,BC=8,点N在BC上,CN=2,E是AB中点,在AC上找一点M使的值最小,此时其最小值一定等于( )
A. 6 B. 8 C. 4 D.
14、如图,已知正三角形ABC的边长为1,E、F、G分别是AB、BC、CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数的图象大致是( )
15、如图,点A是双曲线y=(k>0,x>0)上一动点,AD⊥y轴于D,延长AD交双曲线y=-(x<0)于点B,BC∥y轴交x轴于E,交AO的延长线于点C,则下列说法正确的个数是( )
①当k=1时,四边形AOEB的面积是4.5②当△EOC的面积是4时,k=2
③当k一定时,BD∶AD的值一定④当点A离原点O最近时,且AO=OC,则OB=2
A.1个 B.2个 C.3个 D.4个
16、⊙O的半径为2cm,过点O向直线l引垂线,垂足为A,OA的长为3cm,将直线l沿AO方向平移,使直线l与⊙O相切,那么平移的距离为( )
A. 1cm B. 3cm C. 3cm或5cm D. 1cm或5cm
17、如图,反比例函数的图象与直线的交点为,,过点作轴的平行线与过点作轴的平行线相交于点,则的面积为( )
A. B. C. D.
18、如图,△ABC中,AB=,AC=2,将线段AC绕点A按逆时针方向旋转60°,交BC的延长线于D,则下列关于此图形的一些说法中正确的有( )
⑴ △ACD是等边三角形; ⑵ ∠B=30° ;
⑶ △ABD是直角三角形; ⑷ 点C是BD的中点.
A.1 个 B.2个 C.3个 D.4个
19、某商场出售甲、乙两种不同价格的笔记本电脑,其中甲电脑因供不应求,连续两次提价10%,而乙电脑因外观过时而滞销,只得连续两次降价10%,最后甲、乙两种电脑均以9801元售出。若商场同时售出甲、乙电脑各一台与价格不升不降比较,商场的盈利情况是 ( )
A.前后相同 B.少赚598元 C.多赚980.1元 D.多赚490.05元
20、一次函数与反比例函数的图象交于点,则使的的取值范围是( )
A. B. C. D.
21、已知点、点(,)、点(,1),以、、三点为顶点画平行四边形,则第四个顶点不可能在( ).
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
22、如图,在Rt△ABC中,∠A = 900,A C = 6cm,AB= 8cm,把AB边翻折,使AB边落在BC边上,点A落在点E处,折痕为BD,则sin∠DBE的值为( )A. B. C. D.
23、若二次函数y=2 x2-2 mx+2 m2-2的图象的顶点在y 轴上,则m 的值是( )
(A)0 (B)±1 (C)±2 (D)±
24、如图,正方形ABCD的边长为2,点E在AB边上.四边形EFGB也为正方形,设△AFC的面积为S,则 ( )
A.S=2 B.S=2.4 C.S=4 D.S与BE长度有关
25、如图,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积和为__________
26、如图a,ABCD是一矩形纸片,AB=6cm,AD=8cm,E是AD上一点,且AE=6cm。操作:
(1)将AB向AE折过去,使AB与AE重合,得折痕AF,如图b;(2)将△AFB以BF为折痕向右折过去,得图c。则△GFC的面积是_________
27、如果点P在坐标轴上,以点P为圆心,为半径的圆与直线:相切,则点P的坐标是
28、已知关于的不等式组只有四个整数解,则实数的取值范围是 .
29、已知等腰三角形一腰上的中线将它的周长分为9和12两部分,则腰长为_______.底边长为_______.
30、如图,PA、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点C在上,若PA长为2,则△PEF的周长是_ _.
31、如图,矩形AOCB的两边OC、OA分别位于x轴、y轴上,点B的坐标为B(-,5),D是AB边上的一点,将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在一反比例函数的图像上,那么该函数的解析式是_________.
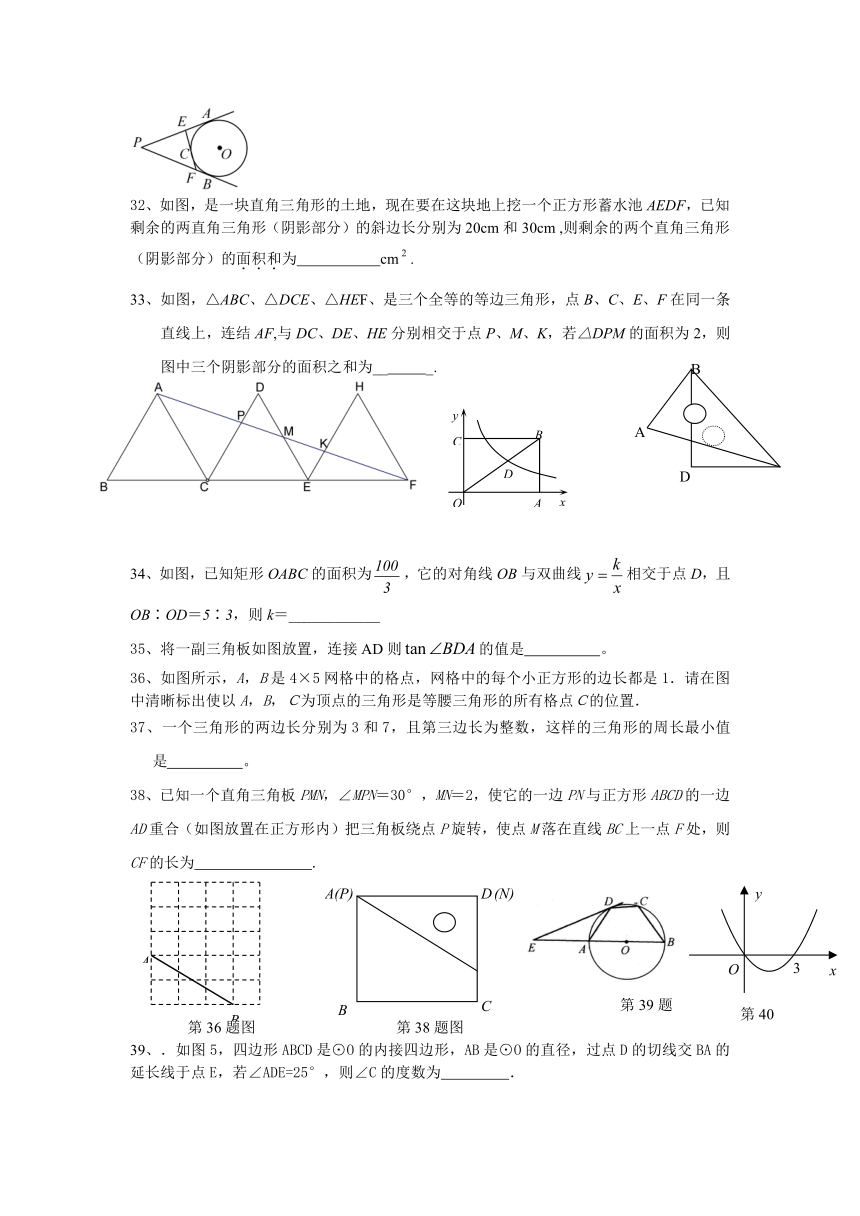
32、如图,是一块直角三角形的土地,现在要在这块地上挖一个正方形蓄水池AEDF,已知剩余的两直角三角形(阴影部分)的斜边长分别为20cm和30cm ,则剩余的两个直角三角形(阴影部分)的面积和为 cm.
33、如图,△ABC、△DCE、△HEF、是三个全等的等边三角形,点B、C、E、F在同一条直线上,连结AF,与DC、DE、HE分别相交于点P、M、K,若△DPM的面积为2,则图中三个阴影部分的面积之和为__ _.
34、如图,已知矩形OABC的面积为,它的对角线OB与双曲线相交于点D,且OB∶OD=5∶3,则k=____________
35、将一副三角板如图放置,连接AD则的值是 。
36、如图所示,A,B是4×5网格中的格点,网格中的每个小正方形的边长都是1.请在图中清晰标出使以A,B,C为顶点的三角形是等腰三角形的所有格点C的位置.
37、一个三角形的两边长分别为3和7,且第三边长为整数,这样的三角形的周长最小值是 。
38、已知一个直角三角板PMN,∠MPN=30°,MN=2,使它的一边PN与正方形ABCD的一边AD重合(如图放置在正方形内)把三角板绕点P旋转,使点M落在直线BC上一点F处,则CF的长为 .
第39题
第36题图 第38题图
39、.如图5,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,过点D的切线交BA的延长线于点E,若∠ADE=25°,则∠C的度数为 .
40.二次函数的图象如图所示,则当>0时的取值范围是 .
41、已知A、B、C三点在同一条直线上,M、N分别为线段AB 、BC的中点,且 AB = 60,BC = 40,则MN 的长为 .
42、如图,⊙O是△ABC的外接圆,⊙O的半径为2,sinB = ,则弦AC的长为___________.
43、如图,在Rt△ABC中,∠C=90°,四边形CDEF为其内接正方形,若AE=2cm,BE=1cm,则图中阴影部分的面积为 cm2.
第44题
44、已知△ABC的面积为36,将△ABC沿BC的方向平移到△A/B /C /的位置,使B / 和C重合,连结AC / 交A/C于D,则△C /DC的面积为___________.
45、已知函数y=kx+b的图像与y轴交点的纵坐标为-5,且x=1时,y=2,则kb=_________.
46. 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,将直角梯形ABCD沿CE折叠,
使点D落在AB上的F点,若AB=BC=12,EF=10,∠FCD=90°,则AF=______.
第46题
47、如图,已知直线与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的函数解析式是__________________.
48、如图,矩形中,,,对角线的垂直平分线分别交, 于点、,连接,则的长为________.
49、如图,在等腰梯形ABCD中,AD∥BC,BC=,AD=,∠B=450,直角三角板含450角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F。若△ABE为等腰三角形,则CF的长等于 .
50、如图,两个同心圆,大圆半径为5cm,小圆的半径为4cm,若大圆的弦AB与小圆有两个公共点,则AB的取值范围是 .
51、如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是_____________.
52、如果三角形的三边长分别为3 、4和5,那么连接这个三角形三边中点,所得的三角形的周长是
53、如图,在平面直角坐标系中,函数(k>0)的图象经过点、两点,过
点A作x轴的垂线,垂足为,连结AB、BC.若的面积为3,则点的坐标为 .
第54题图
54、如图,梯形ABCD中,AD∥BC,∠D=90°,以AB为直径的⊙O与CD相切于E,与BC相交于F,若AB=4,AD=1,则图中两阴影部分面积之和为 .
55、如图,⊙O的半径为12cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以2的速度沿圆周逆时针运动,当点P回到点 就停止运动.当点P运动的时间为 s时,BP与⊙O相切.
56. 如图,正方形网格中,每个小正方形的边长为1,在网格上的三角形中,点B到BC的距离是 .
57、如图,在△ABC中,∠ACB=90,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A在x轴运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离为 .
58、如图,正方形的边长为cm,正方形的边长为cm.如果正方形绕点旋转一周,那么、两点之间的最小距离为 cm.
59、已知平面上四点,,,,直线将四边形 分成面积相等的两部分,则的值为 .
60、如图,矩形内有两个相邻的正方形,面积分别为4和9,那么阴影部分的面积为 .
61.如图,在等边△ABC中,AC=3,点O在AC上,且AO=1.点P是AB上一点,连接OP,以线段OP为一边作正△OPD,且O、P、D三点依次呈逆时针方向,当点D恰好落在边BC上时则AP的长是 .
62、如图,在Rt△ABC内有边长分别为a,b,c的三个正方形,则a,b,c满足的关系式是 .
63、如图,梯形ABCD中,AB∥DC,∠ADC+∠BCD=90°且DC=2AB,分别以DA、AB、BC为边向梯形外作正方形,其面积分别为、、,则、、之间的关系是
64、正方形ABCD中,AB=1,分别以A、C为圆心作两个半径为R、r(R>r)的圆,当R、r满足条件 时,⊙A与⊙C有2个交点.
65.已知△ABC为等腰三角形,由A点作BC边的高恰好等于BC边长的一半,则∠BAC的度数为 .
66、把两块含有300的相同的直角尺按如图所示摆放,使点C、B、E在同一条直线上,连结CD,若AC=6cm,则ΔBCD的面积是 cm2.
67、如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数y=(x>0)的图象上,直角顶点A、B均在轴上,则点B的坐标为 ( )
68、如图,在△ABC中,边AB的垂直平分线分别交AB、BC于点D、E , 边AC的垂直平分线分别交AC、BC于点F、G.若BC=4 ㎝ ,则△AEG的周长是 ㎝.
69、如图:六边形ABCDEF中,AB平行且等于ED、AF平行且等于CD、BC平行且等于FE,对角线FD⊥BD. 已知FD=5cm,BD=4cm. 则六边形ABCDEF的面积是 cm2.
70、如图,将等腰直角三角形按图示方式翻折,若DE=2,下列说法正确的个数有( )
①△BC′D是等腰三角形;②△CED的周长等于BC的长;③DC′平分∠BDE;④BE长为。
A. 1个 B.2个 C.3个 D.4个
71、在一仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来.如图所示,则这堆正方体货箱共有 箱.
73、设直线l1是函数y=2x-4的图象,将直线l1绕原点按逆时针方向旋转90°得到直线l2,则l2与两条坐标轴所围成的三角形的面积是 .
74、某校九年级学生开展了丰富多彩的数学课题学习活动。
在探讨《美丽的正六边形》课题学习时发现正六边形可以分成八个全等的直角梯形(如图15-1),也可以分成八个全等的等腰梯形(如图15-2),若正六边形的边长为,则直角梯形的最短边为 ;等腰梯形的腰长为 .
75、如图,PA、PB是⊙O的两条切线,切点分别为A、B若直径AC=12cm, ∠P=600,则AB的长为 .
76、根据如图所示的程序计算,若输入x的值为1,则输出y的值为 .
77、直角坐标系中,点A(0,0),B(2,0),C(0,2),若有一三角形与△ABC全等,且有一条边与BC重合,那么这个三角形的另一个顶点坐标是 .
78、下列四个图都是平面图形
(1)数一数每个图各有几个顶点,几条边,这些边围成了多少个区域,完成填表
(2)观察上表,你发现顶点数(a)、边数(b)、区域数(c)
之间存在的关系式是
(3)任意画几个图形,验证你的结论是否成立
(4)若已知某个平面图有100个顶点和100个区域,试根据你
所推断出来的关系,确定这个图有多少条边?
79、用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形。设格点多边形的面积为S,它各边上格点的个数和为。
(1)上图中的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请写出S与之间的关系式。
答:S= 。
多边形的序号 ① ② ③ ④ …
多边形的面积S 2 2.5 3 4 …
各边上格点的个数和 4 5 6 8 …
(2)请你再画出一些格点多边形,使这些多边形内部都有而且只有2格点。此时所画的各个多边形的面积S与它各边上格点的个数和之间的关系式是:S= 。
(3)请你继续探索,当格点多边形内部有且只有个格点时,猜想S与有怎样的关系?答:S= 。
80、下列图形中,图(a)是正方体木块,把它切去一块,得到如图(b)(c)(d)(e)的木块.
(1)我们知道,图(a)的正方体木块有8个顶点、12条棱、6个面,请你将图(b)、(c)、(d)、(e)中木块的顶点数、棱数、面数填入下表:
图号 顶点数x 棱数y 面数z
(a) 8 12 6
(b)
(c)
(d)
(e)
(2)上表,各种木块的顶点数、棱数、面数之间的数量关系可以归纳出一定的规律,请你试写出顶点数x、棱数y、面数z之间的数量关系式.
81、在数学上,把部分与整体以某种形式相似的图形,称为分形。如图是形如雪花的分形图案,是瑞典数学家科赫将雪花理想化后得到的科赫雪花曲线,它的作法是在等边三角形每条边的中央分别向外作等边三角形,边长是原三角形边长的三分之一,就得到了一个六角形,这叫做一次生长;把六角形每条边的中央分别向外作等边三角形,边长是六角形边长的三分之一,这叫做二次生长。依照此法,无限制的进行下去,就可以得到漂亮的雪花曲线了
设原等边三角形的边长为a ,面积为s,请你探索:
1.填写下表
边长 边数
一次生长 12
二次生长
三次生长
…… …… ……
n次生长
2. 设第n次生长后的周长记为cn,若cn>100,请用计算器探索的最小值。
3. 设第n次生长后的面积记为Sn ,当n足够大时, sn值能超过原等边三角形面积的2倍吗?请你计算s1,,s2的值,并直接做出判断。
82、如图(1)所示,是一块边长为2的正方形瓷砖,其中瓷砖的阴影部分是半径为1的扇形.请你用这种瓷砖拼出三种不同的图案.使拼成的图案既是轴对称图形又是中心对称图形,把它们分别画在下面边长为4的正方形(2)(3)(4)中(要求用圆规画图).并在每个图中画出其中一条对称轴。
第1题
第7题
B
C
M
P
A
N
C
E
B
A
F
D
第9题
A
B
C
D
M
N
P
P1
M1
N1
A
H
C
D
E
B
A
B
C
D
E
N
A
O
B
C
第17题
(第18题)
A1
A2
A3
A4
E
A
A
A
B
B
B
C
C
C
G
D
D
D
F
F
F
图a
图b
图c
A
B
D
A
B
C
D
O
x
y
3
第40
y
x
O
A
B
A(P)
D
B
C
(N)
E
C
D
A
B
F
(第43题)
(第42题)
O
C
B
A
O
B
C
D
A
F
E
第48题图
第51题图
D
A
B
C
P
M
N
A
B
第50题图
·
A
P
B
O
第55题
第53题
第15题
E
A
B
C
D
G
F
第58题图
A
B
C
O
P
D
第61题图
第8题图
第63题
A
B
D
C
第62题图
(第68题)
左视图
主视图
俯视图
第76题图
第75题图
1、如图:圆的直径垂直弦于,且是半径的中点,,则直径AB的长是( )
(A) (B) (C) (D)
第3题
2、一次函数图象与反比例函数图象的交点情况是( )
(A) 只有一个交点,坐标是(2,3) (B) 只有一个交点,坐标是(-1,6)
(C) 有两个交点,坐标是(2,3)、(3,2) (D)没有交点
3、函数y=kx+b(k、b为常数)的图象如图所示,则不等式kx+b>0的解集是( )
A.x>0 B.x<0 C.x<2 D.x>2
4、小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图所示.若返回时上坡、下坡的速度仍保持不变,那么小明从学校骑车回家用的时间是( )
( A ) 37.2分钟 (B) 48分钟 (C ) 30分钟 ( D )33分钟
5、如图,点A在反比例函数的图象上,点B在反比例函数的图象上,且,则的值是( )
A、 B、 C、 D、
6、如图,在等腰三角形ABC中,∠ABC=120°,点P是底边AC上的一个动点,M,N分别是AB,BC上的动点,若PM+PN的最小值为2,则△ABC的周长是( ).
A.12 B.2+ C.4 D.4+
7、如图,以AB为直径的半圆O上有两点D、E,ED与BA的延长线交于点C,且有DC=OE,若∠C=20°,则∠EOB的度数是( )
(A)40° (B)50° (C)60° (D)80°
8、在一个暗箱里放有m个除颜色外其它完全相同的球,这m个球中红球只有3个.每次将球搅拌均匀后,任意一个球记下颜色后再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在20%,那么可以推算出m大约是( )
A.15 B.9 C. 6 D. 3
9、如图,在等腰中,,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持.连接DE、DF、EF.在此运动变化过程中,下列结论:①是等腰直角三角形; ②四边形CDFE不可能为正方形,
③△CDE与△DAF不可能全等; ④四边形CDFE的面积保持不变;
⑤△CDE面积的最大值为8.
其中正确的结论是( )
A.①②③ B.①③④ C.③④⑤ D.①④⑤
10、在下图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是 ( )
A. 点A B. 点B C. 点C D. 点D
11、如图, 在△ABC中,,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,且、小马虎在研究时得到四个结论:①∠ABC=45° ②AH=BC ③AE-BE=CH④⊿AEC是等腰直角三角形.你认为正确的序号是( )
A. ①②③④ B.②③④ C.①②③ D.②③
12、已知正方形内接于圆心角为90°,半径为10的扇形(即正方形的各顶点都在扇形上),则这个正方形的边长为( )
13、如图,已知梯形ABCD,AD∥BC,,BC=8,点N在BC上,CN=2,E是AB中点,在AC上找一点M使的值最小,此时其最小值一定等于( )
A. 6 B. 8 C. 4 D.
14、如图,已知正三角形ABC的边长为1,E、F、G分别是AB、BC、CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数的图象大致是( )
15、如图,点A是双曲线y=(k>0,x>0)上一动点,AD⊥y轴于D,延长AD交双曲线y=-(x<0)于点B,BC∥y轴交x轴于E,交AO的延长线于点C,则下列说法正确的个数是( )
①当k=1时,四边形AOEB的面积是4.5②当△EOC的面积是4时,k=2
③当k一定时,BD∶AD的值一定④当点A离原点O最近时,且AO=OC,则OB=2
A.1个 B.2个 C.3个 D.4个
16、⊙O的半径为2cm,过点O向直线l引垂线,垂足为A,OA的长为3cm,将直线l沿AO方向平移,使直线l与⊙O相切,那么平移的距离为( )
A. 1cm B. 3cm C. 3cm或5cm D. 1cm或5cm
17、如图,反比例函数的图象与直线的交点为,,过点作轴的平行线与过点作轴的平行线相交于点,则的面积为( )
A. B. C. D.
18、如图,△ABC中,AB=,AC=2,将线段AC绕点A按逆时针方向旋转60°,交BC的延长线于D,则下列关于此图形的一些说法中正确的有( )
⑴ △ACD是等边三角形; ⑵ ∠B=30° ;
⑶ △ABD是直角三角形; ⑷ 点C是BD的中点.
A.1 个 B.2个 C.3个 D.4个
19、某商场出售甲、乙两种不同价格的笔记本电脑,其中甲电脑因供不应求,连续两次提价10%,而乙电脑因外观过时而滞销,只得连续两次降价10%,最后甲、乙两种电脑均以9801元售出。若商场同时售出甲、乙电脑各一台与价格不升不降比较,商场的盈利情况是 ( )
A.前后相同 B.少赚598元 C.多赚980.1元 D.多赚490.05元
20、一次函数与反比例函数的图象交于点,则使的的取值范围是( )
A. B. C. D.
21、已知点、点(,)、点(,1),以、、三点为顶点画平行四边形,则第四个顶点不可能在( ).
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
22、如图,在Rt△ABC中,∠A = 900,A C = 6cm,AB= 8cm,把AB边翻折,使AB边落在BC边上,点A落在点E处,折痕为BD,则sin∠DBE的值为( )A. B. C. D.
23、若二次函数y=2 x2-2 mx+2 m2-2的图象的顶点在y 轴上,则m 的值是( )
(A)0 (B)±1 (C)±2 (D)±
24、如图,正方形ABCD的边长为2,点E在AB边上.四边形EFGB也为正方形,设△AFC的面积为S,则 ( )
A.S=2 B.S=2.4 C.S=4 D.S与BE长度有关
25、如图,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积和为__________
26、如图a,ABCD是一矩形纸片,AB=6cm,AD=8cm,E是AD上一点,且AE=6cm。操作:
(1)将AB向AE折过去,使AB与AE重合,得折痕AF,如图b;(2)将△AFB以BF为折痕向右折过去,得图c。则△GFC的面积是_________
27、如果点P在坐标轴上,以点P为圆心,为半径的圆与直线:相切,则点P的坐标是
28、已知关于的不等式组只有四个整数解,则实数的取值范围是 .
29、已知等腰三角形一腰上的中线将它的周长分为9和12两部分,则腰长为_______.底边长为_______.
30、如图,PA、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点C在上,若PA长为2,则△PEF的周长是_ _.
31、如图,矩形AOCB的两边OC、OA分别位于x轴、y轴上,点B的坐标为B(-,5),D是AB边上的一点,将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在一反比例函数的图像上,那么该函数的解析式是_________.
32、如图,是一块直角三角形的土地,现在要在这块地上挖一个正方形蓄水池AEDF,已知剩余的两直角三角形(阴影部分)的斜边长分别为20cm和30cm ,则剩余的两个直角三角形(阴影部分)的面积和为 cm.
33、如图,△ABC、△DCE、△HEF、是三个全等的等边三角形,点B、C、E、F在同一条直线上,连结AF,与DC、DE、HE分别相交于点P、M、K,若△DPM的面积为2,则图中三个阴影部分的面积之和为__ _.
34、如图,已知矩形OABC的面积为,它的对角线OB与双曲线相交于点D,且OB∶OD=5∶3,则k=____________
35、将一副三角板如图放置,连接AD则的值是 。
36、如图所示,A,B是4×5网格中的格点,网格中的每个小正方形的边长都是1.请在图中清晰标出使以A,B,C为顶点的三角形是等腰三角形的所有格点C的位置.
37、一个三角形的两边长分别为3和7,且第三边长为整数,这样的三角形的周长最小值是 。
38、已知一个直角三角板PMN,∠MPN=30°,MN=2,使它的一边PN与正方形ABCD的一边AD重合(如图放置在正方形内)把三角板绕点P旋转,使点M落在直线BC上一点F处,则CF的长为 .
第39题
第36题图 第38题图
39、.如图5,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,过点D的切线交BA的延长线于点E,若∠ADE=25°,则∠C的度数为 .
40.二次函数的图象如图所示,则当>0时的取值范围是 .
41、已知A、B、C三点在同一条直线上,M、N分别为线段AB 、BC的中点,且 AB = 60,BC = 40,则MN 的长为 .
42、如图,⊙O是△ABC的外接圆,⊙O的半径为2,sinB = ,则弦AC的长为___________.
43、如图,在Rt△ABC中,∠C=90°,四边形CDEF为其内接正方形,若AE=2cm,BE=1cm,则图中阴影部分的面积为 cm2.
第44题
44、已知△ABC的面积为36,将△ABC沿BC的方向平移到△A/B /C /的位置,使B / 和C重合,连结AC / 交A/C于D,则△C /DC的面积为___________.
45、已知函数y=kx+b的图像与y轴交点的纵坐标为-5,且x=1时,y=2,则kb=_________.
46. 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,将直角梯形ABCD沿CE折叠,
使点D落在AB上的F点,若AB=BC=12,EF=10,∠FCD=90°,则AF=______.
第46题
47、如图,已知直线与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的函数解析式是__________________.
48、如图,矩形中,,,对角线的垂直平分线分别交, 于点、,连接,则的长为________.
49、如图,在等腰梯形ABCD中,AD∥BC,BC=,AD=,∠B=450,直角三角板含450角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F。若△ABE为等腰三角形,则CF的长等于 .
50、如图,两个同心圆,大圆半径为5cm,小圆的半径为4cm,若大圆的弦AB与小圆有两个公共点,则AB的取值范围是 .
51、如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是_____________.
52、如果三角形的三边长分别为3 、4和5,那么连接这个三角形三边中点,所得的三角形的周长是
53、如图,在平面直角坐标系中,函数(k>0)的图象经过点、两点,过
点A作x轴的垂线,垂足为,连结AB、BC.若的面积为3,则点的坐标为 .
第54题图
54、如图,梯形ABCD中,AD∥BC,∠D=90°,以AB为直径的⊙O与CD相切于E,与BC相交于F,若AB=4,AD=1,则图中两阴影部分面积之和为 .
55、如图,⊙O的半径为12cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以2的速度沿圆周逆时针运动,当点P回到点 就停止运动.当点P运动的时间为 s时,BP与⊙O相切.
56. 如图,正方形网格中,每个小正方形的边长为1,在网格上的三角形中,点B到BC的距离是 .
57、如图,在△ABC中,∠ACB=90,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A在x轴运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离为 .
58、如图,正方形的边长为cm,正方形的边长为cm.如果正方形绕点旋转一周,那么、两点之间的最小距离为 cm.
59、已知平面上四点,,,,直线将四边形 分成面积相等的两部分,则的值为 .
60、如图,矩形内有两个相邻的正方形,面积分别为4和9,那么阴影部分的面积为 .
61.如图,在等边△ABC中,AC=3,点O在AC上,且AO=1.点P是AB上一点,连接OP,以线段OP为一边作正△OPD,且O、P、D三点依次呈逆时针方向,当点D恰好落在边BC上时则AP的长是 .
62、如图,在Rt△ABC内有边长分别为a,b,c的三个正方形,则a,b,c满足的关系式是 .
63、如图,梯形ABCD中,AB∥DC,∠ADC+∠BCD=90°且DC=2AB,分别以DA、AB、BC为边向梯形外作正方形,其面积分别为、、,则、、之间的关系是
64、正方形ABCD中,AB=1,分别以A、C为圆心作两个半径为R、r(R>r)的圆,当R、r满足条件 时,⊙A与⊙C有2个交点.
65.已知△ABC为等腰三角形,由A点作BC边的高恰好等于BC边长的一半,则∠BAC的度数为 .
66、把两块含有300的相同的直角尺按如图所示摆放,使点C、B、E在同一条直线上,连结CD,若AC=6cm,则ΔBCD的面积是 cm2.
67、如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数y=(x>0)的图象上,直角顶点A、B均在轴上,则点B的坐标为 ( )
68、如图,在△ABC中,边AB的垂直平分线分别交AB、BC于点D、E , 边AC的垂直平分线分别交AC、BC于点F、G.若BC=4 ㎝ ,则△AEG的周长是 ㎝.
69、如图:六边形ABCDEF中,AB平行且等于ED、AF平行且等于CD、BC平行且等于FE,对角线FD⊥BD. 已知FD=5cm,BD=4cm. 则六边形ABCDEF的面积是 cm2.
70、如图,将等腰直角三角形按图示方式翻折,若DE=2,下列说法正确的个数有( )
①△BC′D是等腰三角形;②△CED的周长等于BC的长;③DC′平分∠BDE;④BE长为。
A. 1个 B.2个 C.3个 D.4个
71、在一仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来.如图所示,则这堆正方体货箱共有 箱.
73、设直线l1是函数y=2x-4的图象,将直线l1绕原点按逆时针方向旋转90°得到直线l2,则l2与两条坐标轴所围成的三角形的面积是 .
74、某校九年级学生开展了丰富多彩的数学课题学习活动。
在探讨《美丽的正六边形》课题学习时发现正六边形可以分成八个全等的直角梯形(如图15-1),也可以分成八个全等的等腰梯形(如图15-2),若正六边形的边长为,则直角梯形的最短边为 ;等腰梯形的腰长为 .
75、如图,PA、PB是⊙O的两条切线,切点分别为A、B若直径AC=12cm, ∠P=600,则AB的长为 .
76、根据如图所示的程序计算,若输入x的值为1,则输出y的值为 .
77、直角坐标系中,点A(0,0),B(2,0),C(0,2),若有一三角形与△ABC全等,且有一条边与BC重合,那么这个三角形的另一个顶点坐标是 .
78、下列四个图都是平面图形
(1)数一数每个图各有几个顶点,几条边,这些边围成了多少个区域,完成填表
(2)观察上表,你发现顶点数(a)、边数(b)、区域数(c)
之间存在的关系式是
(3)任意画几个图形,验证你的结论是否成立
(4)若已知某个平面图有100个顶点和100个区域,试根据你
所推断出来的关系,确定这个图有多少条边?
79、用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形。设格点多边形的面积为S,它各边上格点的个数和为。
(1)上图中的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请写出S与之间的关系式。
答:S= 。
多边形的序号 ① ② ③ ④ …
多边形的面积S 2 2.5 3 4 …
各边上格点的个数和 4 5 6 8 …
(2)请你再画出一些格点多边形,使这些多边形内部都有而且只有2格点。此时所画的各个多边形的面积S与它各边上格点的个数和之间的关系式是:S= 。
(3)请你继续探索,当格点多边形内部有且只有个格点时,猜想S与有怎样的关系?答:S= 。
80、下列图形中,图(a)是正方体木块,把它切去一块,得到如图(b)(c)(d)(e)的木块.
(1)我们知道,图(a)的正方体木块有8个顶点、12条棱、6个面,请你将图(b)、(c)、(d)、(e)中木块的顶点数、棱数、面数填入下表:
图号 顶点数x 棱数y 面数z
(a) 8 12 6
(b)
(c)
(d)
(e)
(2)上表,各种木块的顶点数、棱数、面数之间的数量关系可以归纳出一定的规律,请你试写出顶点数x、棱数y、面数z之间的数量关系式.
81、在数学上,把部分与整体以某种形式相似的图形,称为分形。如图是形如雪花的分形图案,是瑞典数学家科赫将雪花理想化后得到的科赫雪花曲线,它的作法是在等边三角形每条边的中央分别向外作等边三角形,边长是原三角形边长的三分之一,就得到了一个六角形,这叫做一次生长;把六角形每条边的中央分别向外作等边三角形,边长是六角形边长的三分之一,这叫做二次生长。依照此法,无限制的进行下去,就可以得到漂亮的雪花曲线了
设原等边三角形的边长为a ,面积为s,请你探索:
1.填写下表
边长 边数
一次生长 12
二次生长
三次生长
…… …… ……
n次生长
2. 设第n次生长后的周长记为cn,若cn>100,请用计算器探索的最小值。
3. 设第n次生长后的面积记为Sn ,当n足够大时, sn值能超过原等边三角形面积的2倍吗?请你计算s1,,s2的值,并直接做出判断。
82、如图(1)所示,是一块边长为2的正方形瓷砖,其中瓷砖的阴影部分是半径为1的扇形.请你用这种瓷砖拼出三种不同的图案.使拼成的图案既是轴对称图形又是中心对称图形,把它们分别画在下面边长为4的正方形(2)(3)(4)中(要求用圆规画图).并在每个图中画出其中一条对称轴。
第1题
第7题
B
C
M
P
A
N
C
E
B
A
F
D
第9题
A
B
C
D
M
N
P
P1
M1
N1
A
H
C
D
E
B
A
B
C
D
E
N
A
O
B
C
第17题
(第18题)
A1
A2
A3
A4
E
A
A
A
B
B
B
C
C
C
G
D
D
D
F
F
F
图a
图b
图c
A
B
D
A
B
C
D
O
x
y
3
第40
y
x
O
A
B
A(P)
D
B
C
(N)
E
C
D
A
B
F
(第43题)
(第42题)
O
C
B
A
O
B
C
D
A
F
E
第48题图
第51题图
D
A
B
C
P
M
N
A
B
第50题图
·
A
P
B
O
第55题
第53题
第15题
E
A
B
C
D
G
F
第58题图
A
B
C
O
P
D
第61题图
第8题图
第63题
A
B
D
C
第62题图
(第68题)
左视图
主视图
俯视图
第76题图
第75题图
同课章节目录
