苏科版七年级下册数学课件 第12章 证明 小结与思考(19张PPT)
文档属性
| 名称 | 苏科版七年级下册数学课件 第12章 证明 小结与思考(19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 109.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-19 23:37:49 | ||
图片预览




文档简介
第十二章 小结与思考
知识梳理
1. 叫做命题,_________叫真命题,___________ 叫假命题。
2.证明与图形有关的命题的一般步骤有(1)_________ (2)_________ (3) _________
3. 三角形的内角和为 ,直角三角形的两个锐角 ,三角形的外角等于_____________
4.______________ _________ 叫互逆命题
小题温习
1.下面的句子中是命题的有________________(1)我是扬州人;(2)房间里的花;(3)你吃饭了吗?(4)内错角相等;
(5)延长线段AB; (6)明天可能下雨; (7)若a2>b2 则a>b. (8)对顶角相等;
2.写出下列命题的条件与结论,并判断真假。
(1)相等的两个角是对顶角;条件是_________
结论是_________ 它是()命题
(2)同角的余角相等条件是_________
结论是_________ 它是()命题
;(2)
小题温习
3. (1)命题“内错角相等”的条件是_________,结论是________ ,这个命题的逆命题的条件是___________,结论是__________.
(2)命题“如果a>0,b>0,那么ab>0”的条件是___________,结论是_________,这个命题的逆命题是___________.
小题温习
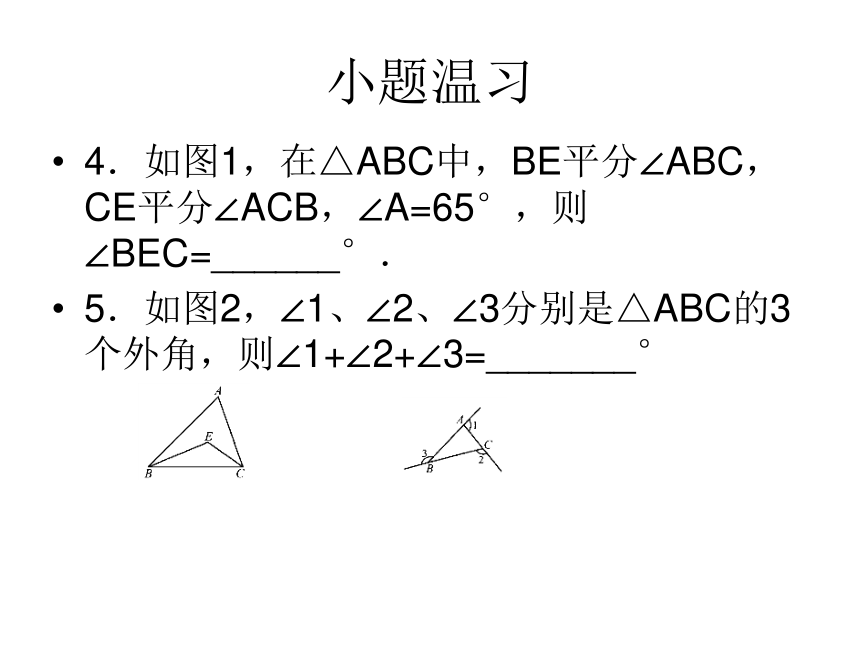
4.如图1,在△ABC中,BE平分∠ABC,CE平分∠ACB,∠A=65°,则∠BEC=______°.
5.如图2,∠1、∠2、∠3分别是△ABC的3个外角,则∠1+∠2+∠3=_______°
小题温习
6.若一个三角形的3个内角度数之比为4:3:2,则这个三角形的最大内角为___°
7.下面有3个命题:①同旁内角互补;②若,则;③垂直于同一直线的两直线互相平行.其中真命题为_________(填序号)
8.下面有3个判断:①一个三角形的3个内角中最多有1个直角;②一个三角形的3个内角中至少有两个锐角;③一个三角形的3个内角中至少有1个钝角.其中正确的有_________(填序号)
典型例题
例1.请把下列证明过程补充完整: 已知:如图,DE∥BC,BE平分∠ABC.求证:∠1=∠3.
证明:因为BE平分∠ABC(已知),
所以∠1=______( ).
又因为DE∥BC(已知),
所以∠2=_____( ).
所以∠1=∠3( ).
典型例题
例2. 如图,在△ABC中,∠A=600,D是AB上一点,E是AC上一点,BE、CD相交于点O,且∠BOD=550,∠ACD=300,求∠ABE的度数。
典型例题
例3.已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.
求证:AD平分∠BAC
典型例题
例4.如图,直线AB和直线CD、直线BE和直线CF都被直线BC所截.在下面在个式
子中,请你选择其中两个作为题设,剩下的一个作为结论,组成一个真命题并证明 ①AB⊥BC,CD⊥BC.;②BE∥CF.③∠l=∠2.
谈谈收获与疑惑
巩固练习
1.下列语言是命题的是( )
A.画两条相等的线段 B.等于同一个角的两个角相等吗?
C.延长线段AO到C,使OC=OA D.两直线平行,内错角相等.
2.下列命题是真命题的是 ( )
A.如果两个角不相等,那么这两个角不是对顶角;
B.锐角三角形中最大的角一定大于或等于60° C.如果a2=b2,那么a=b;
D.如果两角是同位角,那么这两角一定相等
3.举反例说明下列命题是假命题
(1)如果一个角的两边分别与另一个角的两边互相平行,那么这两个角相等
(2)如果a巩固练习
4.写出下列命题的逆命题并判断原命题和逆命题的真假
(1)如果a=0,那么ab=0;
(2)直角都相等;
(3)如果│a│=│b│,那么a=b;
5.如图所示,已知BE平分∠ABC,CE平分∠BCD.另有三个条件:① AB∥CD;②∠1+∠2=90;③∠ABE+∠DCE=∠BEC.以①、②、
③其中一个为条件,另一个为结论组成命题,在级成的所有命题中,
是真命题的个数有 ( )
A.3个 B.4个 C.5个 D.6个
巩固练习
6. 如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
证明:∵DG⊥BC,AC⊥BC(已知),
∴DGB=∠ACB=90(垂直的定义).
∴DG∥AC( )
∴∠2= ( )
∵∠1=∠2(已知)∴∠1= (等量代换).
∴EF∥CD( ).
∴∠AEF=∠ ( )
∵EF⊥AB(已知),∴AEF=( )
∴∠ADC=( )
∴CD⊥AB( ).
巩固练习
7.证明:两条平行线被第三条直线所截,同旁内角的平分线互相垂直。
8.如图,∠ABC=66°,∠ACB=54°,BE是AC边上的高,CF是AB边上的高,H是BE、CF的交点,求∠ABE、∠ACF和∠BHC的度数.
巩固练习
拓展提升
9.探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
如图(1),∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
.
如图(2),在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
如图(3),在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究
∠P与∠A+∠B的数量关系.
探究四:若将上题中的四边形ABCD改为六边形ABCDEF(如图(4))呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系
知识梳理
1. 叫做命题,_________叫真命题,___________ 叫假命题。
2.证明与图形有关的命题的一般步骤有(1)_________ (2)_________ (3) _________
3. 三角形的内角和为 ,直角三角形的两个锐角 ,三角形的外角等于_____________
4.______________ _________ 叫互逆命题
小题温习
1.下面的句子中是命题的有________________(1)我是扬州人;(2)房间里的花;(3)你吃饭了吗?(4)内错角相等;
(5)延长线段AB; (6)明天可能下雨; (7)若a2>b2 则a>b. (8)对顶角相等;
2.写出下列命题的条件与结论,并判断真假。
(1)相等的两个角是对顶角;条件是_________
结论是_________ 它是()命题
(2)同角的余角相等条件是_________
结论是_________ 它是()命题
;(2)
小题温习
3. (1)命题“内错角相等”的条件是_________,结论是________ ,这个命题的逆命题的条件是___________,结论是__________.
(2)命题“如果a>0,b>0,那么ab>0”的条件是___________,结论是_________,这个命题的逆命题是___________.
小题温习
4.如图1,在△ABC中,BE平分∠ABC,CE平分∠ACB,∠A=65°,则∠BEC=______°.
5.如图2,∠1、∠2、∠3分别是△ABC的3个外角,则∠1+∠2+∠3=_______°
小题温习
6.若一个三角形的3个内角度数之比为4:3:2,则这个三角形的最大内角为___°
7.下面有3个命题:①同旁内角互补;②若,则;③垂直于同一直线的两直线互相平行.其中真命题为_________(填序号)
8.下面有3个判断:①一个三角形的3个内角中最多有1个直角;②一个三角形的3个内角中至少有两个锐角;③一个三角形的3个内角中至少有1个钝角.其中正确的有_________(填序号)
典型例题
例1.请把下列证明过程补充完整: 已知:如图,DE∥BC,BE平分∠ABC.求证:∠1=∠3.
证明:因为BE平分∠ABC(已知),
所以∠1=______( ).
又因为DE∥BC(已知),
所以∠2=_____( ).
所以∠1=∠3( ).
典型例题
例2. 如图,在△ABC中,∠A=600,D是AB上一点,E是AC上一点,BE、CD相交于点O,且∠BOD=550,∠ACD=300,求∠ABE的度数。
典型例题
例3.已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.
求证:AD平分∠BAC
典型例题
例4.如图,直线AB和直线CD、直线BE和直线CF都被直线BC所截.在下面在个式
子中,请你选择其中两个作为题设,剩下的一个作为结论,组成一个真命题并证明 ①AB⊥BC,CD⊥BC.;②BE∥CF.③∠l=∠2.
谈谈收获与疑惑
巩固练习
1.下列语言是命题的是( )
A.画两条相等的线段 B.等于同一个角的两个角相等吗?
C.延长线段AO到C,使OC=OA D.两直线平行,内错角相等.
2.下列命题是真命题的是 ( )
A.如果两个角不相等,那么这两个角不是对顶角;
B.锐角三角形中最大的角一定大于或等于60° C.如果a2=b2,那么a=b;
D.如果两角是同位角,那么这两角一定相等
3.举反例说明下列命题是假命题
(1)如果一个角的两边分别与另一个角的两边互相平行,那么这两个角相等
(2)如果a
4.写出下列命题的逆命题并判断原命题和逆命题的真假
(1)如果a=0,那么ab=0;
(2)直角都相等;
(3)如果│a│=│b│,那么a=b;
5.如图所示,已知BE平分∠ABC,CE平分∠BCD.另有三个条件:① AB∥CD;②∠1+∠2=90;③∠ABE+∠DCE=∠BEC.以①、②、
③其中一个为条件,另一个为结论组成命题,在级成的所有命题中,
是真命题的个数有 ( )
A.3个 B.4个 C.5个 D.6个
巩固练习
6. 如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
证明:∵DG⊥BC,AC⊥BC(已知),
∴DGB=∠ACB=90(垂直的定义).
∴DG∥AC( )
∴∠2= ( )
∵∠1=∠2(已知)∴∠1= (等量代换).
∴EF∥CD( ).
∴∠AEF=∠ ( )
∵EF⊥AB(已知),∴AEF=( )
∴∠ADC=( )
∴CD⊥AB( ).
巩固练习
7.证明:两条平行线被第三条直线所截,同旁内角的平分线互相垂直。
8.如图,∠ABC=66°,∠ACB=54°,BE是AC边上的高,CF是AB边上的高,H是BE、CF的交点,求∠ABE、∠ACF和∠BHC的度数.
巩固练习
拓展提升
9.探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
如图(1),∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
.
如图(2),在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
如图(3),在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究
∠P与∠A+∠B的数量关系.
探究四:若将上题中的四边形ABCD改为六边形ABCDEF(如图(4))呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
