12.3 角的平分线的性质课件(共27张PPT)
文档属性
| 名称 | 12.3 角的平分线的性质课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-20 09:03:41 | ||
图片预览






文档简介
(共27张PPT)
人教版
八年级数学上
12.3
角平分线的性质
学习目标
1.通过操作、验证等方式,探究并掌握角平分线的性质和判定
定理.(难点)
2.能运用角的平分线性质和判定解决简单的几何问题.
(重点)
情境导入
思考1:在纸上画一个角,你能得到这个角的平分线吗?
用量角器度量,也可用折纸的方法.
思考2:如果把前面的纸片换成木板、钢板等,还能用对折的方
法得到木板、钢板的角平分线吗?
不能。
合作探究---作一个角的平分线
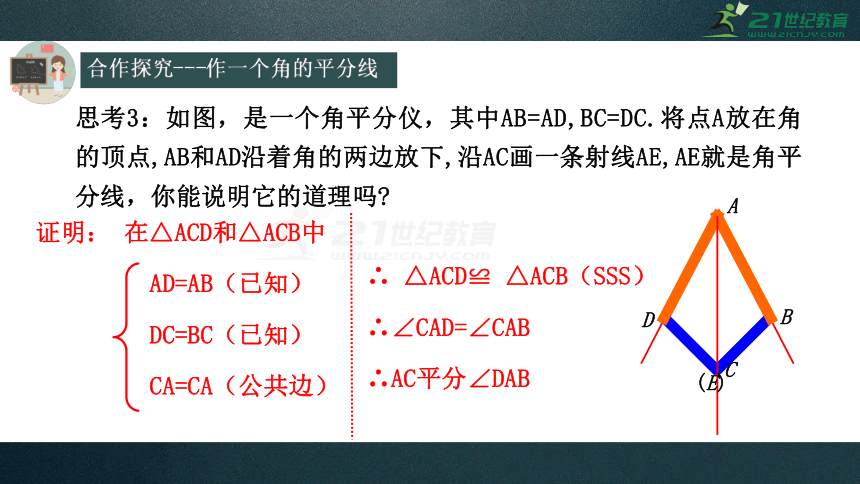
思考3:如图,是一个角平分仪,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,你能说明它的道理吗?
A
B
C
(E)
D
证明:
在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
∴
△ACD≌
△ACB(SSS)
∴∠CAD=∠CAB
∴AC平分∠DAB
合作探究---作一个角的平分线
思考4:如果没有此仪器,我们用数学直尺、圆规作图工具,根据该仪器的设计思路,能作出一个角的平分线吗?
A
B
O
提示:
(1)已知什么?求作什么?
(2)把平分角的仪器放在角的两边,仪器的顶点与角的顶点重合,且仪器的两边相等,怎样在作图中体现这个过程呢?
(3)在平分角的仪器中,BC=DC,怎样在作图中体现这个过程呢?
(4)你能说明为什么OC是∠AOB的平分线吗?
合作探究---作一个角的平分线
A
B
M
N
C
O
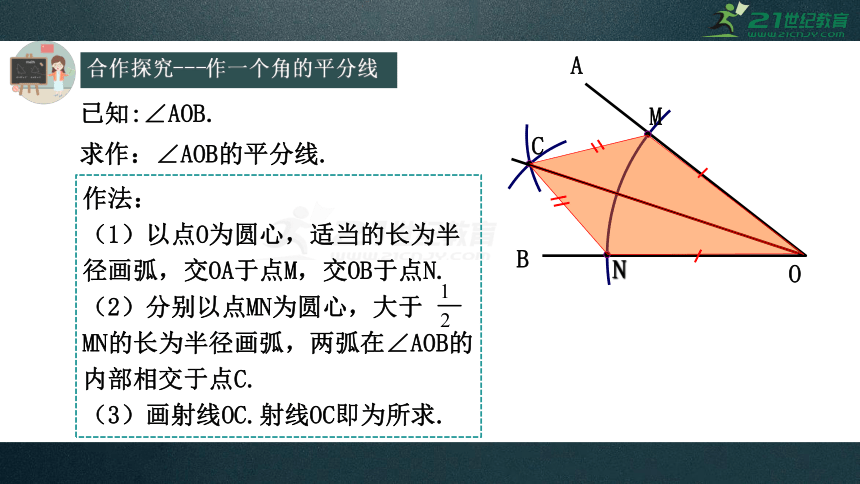
已知:∠AOB.
求作:∠AOB的平分线.
作法:
(1)以点O为圆心,适当的长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点MN为圆心,大于
MN的长为半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC.射线OC即为所求.
合作探究---角平分线的性质
1.
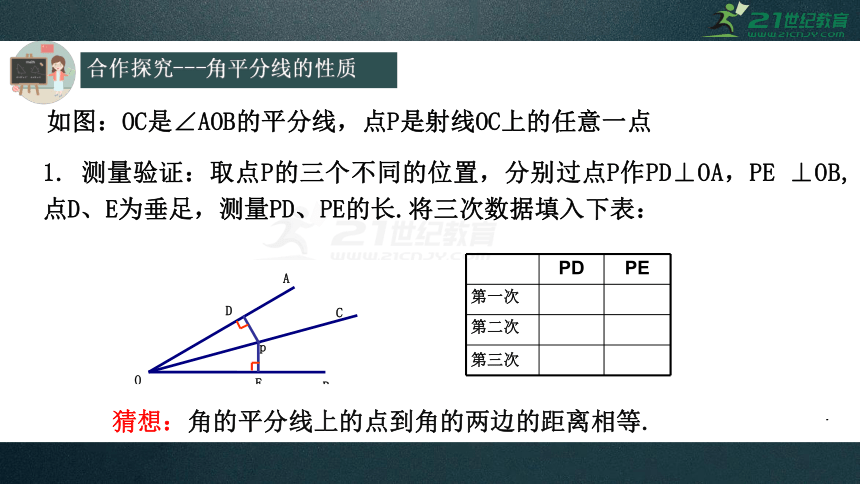
测量验证:取点P的三个不同的位置,分别过点P作PD⊥OA,PE
⊥OB,点D、E为垂足,测量PD、PE的长.将三次数据填入下表:
2.
观察测量结果,猜想线段PD与PE的大小关系,写出结:__________
PD
PE
第一次
第二次
第三次
C
O
B
A
PD=PE
p
D
E
如图:OC是∠AOB的平分线,点P是射线OC上的任意一点
猜想:角的平分线上的点到角的两边的距离相等.
合作探究---角平分线的性质
已知:如图,
∠AOC=
∠BOC,点P在OC上,PD⊥OA,PE⊥OB,
垂足分别为D,E.求证:PD=PE.
P
A
O
B
C
D
E
证明:
∵
PD⊥OA,PE⊥OB,
∴
∠PDO=
∠PEO=90
°.
在△PDO和△PEO中,
∠PDO=
∠PEO,
∠AOC=
∠BOC,
OP=
OP,
∴
△PDO
≌△PEO(AAS).
∴PD=PE.
3.推理证明:角的平分线上的点到角的两边的距离相等
合作探究---角平分线的性质
归纳总结:
一般情况下,我们要证明一个几何命题时,可以按照类似的步骤进行,即
1.明确命题中的已知和求证;
2.根据题意,画出图形,并用数学符号表示已知和求证;
3.经过分析,找出由已知推出要证的结论的途径,写出证明过程.
合作探究---角平分线的性质
角的平分线上的点到角的两边的距离相等.
应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离.
定理的作用:
证明线段相等.
应用格式:
∵OP
是∠AOB的平分线,
∴PD
=
PE
PD⊥OA,PE⊥OB,
B
A
D
O
P
E
C
角的平分线的性质:
典例精析
例1:已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,
DF⊥AC.垂足分别为E,F.求证:EB=FC.
A
B
C
D
E
F
证明:
∵AD是∠BAC的角平分线,
DE⊥AB,
DF⊥AC,
∴
DE=DF,
∠DEB=∠DFC=90
°.
在Rt△BDE
和
Rt△CDF中,
DE=DF,
BD=CD,
∴
Rt△BDE
≌
Rt△CDF(HL).
∴
EB=FC.
小试牛刀
A
B
C
P
(2)求△APB的面积.
D
(3)求?PDB的周长.
·AB·PD
=28.
由垂直平分线的性质,
可知,PD=PC=4,
=
1、如图,在Rt△ABC中,AC=BC,∠C=90°,AP平分∠BAC交BC于点P,若PC=4,
AB=14.(1)则点P到AB的距离为_______.
4
合作探究---角平分线的判定
思考:我们知道,角平分线上的点到角的两边的距离相等.那么到角的两边的距离相等的点是否在角的平分线上呢?
猜测:到角的两边的距离相等的点在角的平分线上.
合作探究---角平分线的性质
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=PE.
求证:点P在∠AOB的角平分线上.
证明:
作射线OP,
∴点P在∠AOB
角的平分线上.
在Rt△PDO和Rt△PEO
中,
(全等三角形的对应角相等).
OP=OP(公共边),
PD=
PE(已知
),
B
A
D
O
P
E
∵PD⊥OA,PE⊥OB.
∴∠PDO=∠PEO=90°,
∴Rt△PDO≌Rt△PEO(
HL).
∴∠AOP=∠BOP
合作探究---角平分线的判定
判定定理:
角的内部到角的两边的距离相等的点在角的平分线上.
P
A
O
B
C
D
E
应用所具备的条件:
(1)位置关系:点在角的内部;
(2)数量关系:该点到角两边的距离相等.
定理的作用:判断点是否在角平分线上.
应用格式:
∵
PD⊥OA,PE⊥OB,PD=PE.
∴点P
在∠AOB的平分线上.
典例精析
例2:如图,要在S区建一个贸易市场,使它到铁路和公路距离相等,
离公路与铁路交叉处500米,这个集贸市场应建在何处(比例尺为1︰20000)?
D
C
S
解:作夹角的角平分线OC,
截取OD=2.5cm
,D即为所求.
O
知识点拨:根据角平分线的判定定理,要求作的点到两边的距离相等,一般需作这两边直线形成的角的平分线,再在这条角平分线上根据要求取点.
典例精析
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE.
同理,PE=PF.
∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等.
证明:过点P作PD⊥AB于D,
PE⊥BC于E,PF⊥AC于F,
例3、如图,△ABC的角平分线BM,CN相交于点P。求证:点P到三边AB、BC、CA的距离相等。
D
P
M
N
A
B
C
F
E
结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.
想一想,点p在角A的平分线上吗?这说明三角形的三条角平分线有什么关系?
小试牛刀
1、如图,在△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等.若∠A=40°,则∠BOC的度数为( )
A.110°
B.120°
C.130°
D.140°
A
小试牛刀
2.
如图所示,已知△ABC中,PE∥AB交BC于点E,PF∥AC交BC于点F,点P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.
解:AD平分∠BAC.理由如下:
∵D到PE的距离与到PF的距离相等,
∴点D在∠EPF的平分线上.
∴∠1=∠2.
又∵PE∥AB,∴∠1=∠3.
同理,∠2=∠4.∴∠3=∠4,∴AD平分∠BAC.
A
B
C
E
F
D
(
(
(
(
3
4
1
2
P
综合演练
1.如图,△ABC中,∠C=90°,AC=BC,AD是∠CAB的平分线,DE⊥AB于E.已知AC=6cm,则BD+DE的和为( )
A.
5cm
B.
6cm
C.
7cm
D.
8cm
B
2、如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论①AS=AR;②QP∥AR;③△BPR≌△QSP中(
)
A.
全部正确
B.
仅①和②正确
C.
仅①正确
D.
仅①和③正确
?
B
综合演练
3.如图所示,D是∠ACG的平分线上的一点.DE⊥AC,DF⊥CG,垂足分别为E,F.求证:CE=CF.
证明:∵CD是∠ACG的平分线,DE⊥AC,DF⊥CG,
∴DE=DF.
在Rt△CDE和Rt△CDF中,
∴Rt△CDE≌Rt△CDF(HL),
∴CE=CF.
综合演练
4.如图,已知∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
证明:
过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M.
∵点F在∠BCE的平分线上,
FG⊥AE,
FM⊥BC.
∴FG=FM.
又∵点F在∠CBD的平分线上,
FH⊥AD,
FM⊥BC,
∴FM=FH,
∴FG=FH.
∴点F在∠DAE的平分线上.
G
H
M
A
B
C
F
E
D
综合演练
5.如图,已知AD∥BC,P是∠BAD与
∠ABC的平分线的交点,PE⊥AB于E,且PE=3,求AD与BC之间的距离.
解:过点P作MN⊥AD于点M,交BC于点N.
∵
AD∥BC,
∴
MN⊥BC,MN的长即为AD与BC之间
的距离.
∵
AP平分∠BAD,
PM⊥AD
,
PE⊥AB,
∴
PM=
PE.同理,
PN=
PE.
∴
PM=
PN=
PE=3.∴
MN=6.即AD与BC之间的距离为6.
学以致用
如图,某个居民小区C附近有三条两两相交的道路MN、OA、OB,拟在MN上建造一个大型超市,使得它到OA、OB的距离相等,请确定该超市的位置P.
小区C
P
A
O
B
M
N
课堂小结
本节课你收获了什么知识?
1、尺规作图,作已知角的角平分线的步骤是什么?
2、角平分线的性质是什么?如何用几何语言来表示?判定呢?
3、角平分线的性质和判定的作用是什么?
课后作业
课本教材第51页:1、3、5题
https://www.21cnjy.com/help/help_extract.php
人教版
八年级数学上
12.3
角平分线的性质
学习目标
1.通过操作、验证等方式,探究并掌握角平分线的性质和判定
定理.(难点)
2.能运用角的平分线性质和判定解决简单的几何问题.
(重点)
情境导入
思考1:在纸上画一个角,你能得到这个角的平分线吗?
用量角器度量,也可用折纸的方法.
思考2:如果把前面的纸片换成木板、钢板等,还能用对折的方
法得到木板、钢板的角平分线吗?
不能。
合作探究---作一个角的平分线
思考3:如图,是一个角平分仪,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,你能说明它的道理吗?
A
B
C
(E)
D
证明:
在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
∴
△ACD≌
△ACB(SSS)
∴∠CAD=∠CAB
∴AC平分∠DAB
合作探究---作一个角的平分线
思考4:如果没有此仪器,我们用数学直尺、圆规作图工具,根据该仪器的设计思路,能作出一个角的平分线吗?
A
B
O
提示:
(1)已知什么?求作什么?
(2)把平分角的仪器放在角的两边,仪器的顶点与角的顶点重合,且仪器的两边相等,怎样在作图中体现这个过程呢?
(3)在平分角的仪器中,BC=DC,怎样在作图中体现这个过程呢?
(4)你能说明为什么OC是∠AOB的平分线吗?
合作探究---作一个角的平分线
A
B
M
N
C
O
已知:∠AOB.
求作:∠AOB的平分线.
作法:
(1)以点O为圆心,适当的长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点MN为圆心,大于
MN的长为半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC.射线OC即为所求.
合作探究---角平分线的性质
1.
测量验证:取点P的三个不同的位置,分别过点P作PD⊥OA,PE
⊥OB,点D、E为垂足,测量PD、PE的长.将三次数据填入下表:
2.
观察测量结果,猜想线段PD与PE的大小关系,写出结:__________
PD
PE
第一次
第二次
第三次
C
O
B
A
PD=PE
p
D
E
如图:OC是∠AOB的平分线,点P是射线OC上的任意一点
猜想:角的平分线上的点到角的两边的距离相等.
合作探究---角平分线的性质
已知:如图,
∠AOC=
∠BOC,点P在OC上,PD⊥OA,PE⊥OB,
垂足分别为D,E.求证:PD=PE.
P
A
O
B
C
D
E
证明:
∵
PD⊥OA,PE⊥OB,
∴
∠PDO=
∠PEO=90
°.
在△PDO和△PEO中,
∠PDO=
∠PEO,
∠AOC=
∠BOC,
OP=
OP,
∴
△PDO
≌△PEO(AAS).
∴PD=PE.
3.推理证明:角的平分线上的点到角的两边的距离相等
合作探究---角平分线的性质
归纳总结:
一般情况下,我们要证明一个几何命题时,可以按照类似的步骤进行,即
1.明确命题中的已知和求证;
2.根据题意,画出图形,并用数学符号表示已知和求证;
3.经过分析,找出由已知推出要证的结论的途径,写出证明过程.
合作探究---角平分线的性质
角的平分线上的点到角的两边的距离相等.
应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离.
定理的作用:
证明线段相等.
应用格式:
∵OP
是∠AOB的平分线,
∴PD
=
PE
PD⊥OA,PE⊥OB,
B
A
D
O
P
E
C
角的平分线的性质:
典例精析
例1:已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,
DF⊥AC.垂足分别为E,F.求证:EB=FC.
A
B
C
D
E
F
证明:
∵AD是∠BAC的角平分线,
DE⊥AB,
DF⊥AC,
∴
DE=DF,
∠DEB=∠DFC=90
°.
在Rt△BDE
和
Rt△CDF中,
DE=DF,
BD=CD,
∴
Rt△BDE
≌
Rt△CDF(HL).
∴
EB=FC.
小试牛刀
A
B
C
P
(2)求△APB的面积.
D
(3)求?PDB的周长.
·AB·PD
=28.
由垂直平分线的性质,
可知,PD=PC=4,
=
1、如图,在Rt△ABC中,AC=BC,∠C=90°,AP平分∠BAC交BC于点P,若PC=4,
AB=14.(1)则点P到AB的距离为_______.
4
合作探究---角平分线的判定
思考:我们知道,角平分线上的点到角的两边的距离相等.那么到角的两边的距离相等的点是否在角的平分线上呢?
猜测:到角的两边的距离相等的点在角的平分线上.
合作探究---角平分线的性质
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=PE.
求证:点P在∠AOB的角平分线上.
证明:
作射线OP,
∴点P在∠AOB
角的平分线上.
在Rt△PDO和Rt△PEO
中,
(全等三角形的对应角相等).
OP=OP(公共边),
PD=
PE(已知
),
B
A
D
O
P
E
∵PD⊥OA,PE⊥OB.
∴∠PDO=∠PEO=90°,
∴Rt△PDO≌Rt△PEO(
HL).
∴∠AOP=∠BOP
合作探究---角平分线的判定
判定定理:
角的内部到角的两边的距离相等的点在角的平分线上.
P
A
O
B
C
D
E
应用所具备的条件:
(1)位置关系:点在角的内部;
(2)数量关系:该点到角两边的距离相等.
定理的作用:判断点是否在角平分线上.
应用格式:
∵
PD⊥OA,PE⊥OB,PD=PE.
∴点P
在∠AOB的平分线上.
典例精析
例2:如图,要在S区建一个贸易市场,使它到铁路和公路距离相等,
离公路与铁路交叉处500米,这个集贸市场应建在何处(比例尺为1︰20000)?
D
C
S
解:作夹角的角平分线OC,
截取OD=2.5cm
,D即为所求.
O
知识点拨:根据角平分线的判定定理,要求作的点到两边的距离相等,一般需作这两边直线形成的角的平分线,再在这条角平分线上根据要求取点.
典例精析
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE.
同理,PE=PF.
∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等.
证明:过点P作PD⊥AB于D,
PE⊥BC于E,PF⊥AC于F,
例3、如图,△ABC的角平分线BM,CN相交于点P。求证:点P到三边AB、BC、CA的距离相等。
D
P
M
N
A
B
C
F
E
结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.
想一想,点p在角A的平分线上吗?这说明三角形的三条角平分线有什么关系?
小试牛刀
1、如图,在△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等.若∠A=40°,则∠BOC的度数为( )
A.110°
B.120°
C.130°
D.140°
A
小试牛刀
2.
如图所示,已知△ABC中,PE∥AB交BC于点E,PF∥AC交BC于点F,点P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.
解:AD平分∠BAC.理由如下:
∵D到PE的距离与到PF的距离相等,
∴点D在∠EPF的平分线上.
∴∠1=∠2.
又∵PE∥AB,∴∠1=∠3.
同理,∠2=∠4.∴∠3=∠4,∴AD平分∠BAC.
A
B
C
E
F
D
(
(
(
(
3
4
1
2
P
综合演练
1.如图,△ABC中,∠C=90°,AC=BC,AD是∠CAB的平分线,DE⊥AB于E.已知AC=6cm,则BD+DE的和为( )
A.
5cm
B.
6cm
C.
7cm
D.
8cm
B
2、如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论①AS=AR;②QP∥AR;③△BPR≌△QSP中(
)
A.
全部正确
B.
仅①和②正确
C.
仅①正确
D.
仅①和③正确
?
B
综合演练
3.如图所示,D是∠ACG的平分线上的一点.DE⊥AC,DF⊥CG,垂足分别为E,F.求证:CE=CF.
证明:∵CD是∠ACG的平分线,DE⊥AC,DF⊥CG,
∴DE=DF.
在Rt△CDE和Rt△CDF中,
∴Rt△CDE≌Rt△CDF(HL),
∴CE=CF.
综合演练
4.如图,已知∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
证明:
过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M.
∵点F在∠BCE的平分线上,
FG⊥AE,
FM⊥BC.
∴FG=FM.
又∵点F在∠CBD的平分线上,
FH⊥AD,
FM⊥BC,
∴FM=FH,
∴FG=FH.
∴点F在∠DAE的平分线上.
G
H
M
A
B
C
F
E
D
综合演练
5.如图,已知AD∥BC,P是∠BAD与
∠ABC的平分线的交点,PE⊥AB于E,且PE=3,求AD与BC之间的距离.
解:过点P作MN⊥AD于点M,交BC于点N.
∵
AD∥BC,
∴
MN⊥BC,MN的长即为AD与BC之间
的距离.
∵
AP平分∠BAD,
PM⊥AD
,
PE⊥AB,
∴
PM=
PE.同理,
PN=
PE.
∴
PM=
PN=
PE=3.∴
MN=6.即AD与BC之间的距离为6.
学以致用
如图,某个居民小区C附近有三条两两相交的道路MN、OA、OB,拟在MN上建造一个大型超市,使得它到OA、OB的距离相等,请确定该超市的位置P.
小区C
P
A
O
B
M
N
课堂小结
本节课你收获了什么知识?
1、尺规作图,作已知角的角平分线的步骤是什么?
2、角平分线的性质是什么?如何用几何语言来表示?判定呢?
3、角平分线的性质和判定的作用是什么?
课后作业
课本教材第51页:1、3、5题
https://www.21cnjy.com/help/help_extract.php
