人教版九年级数学上册:21.2.4 一元二次方程的根与系数的关系 课件(共15张PPT)
文档属性
| 名称 | 人教版九年级数学上册:21.2.4 一元二次方程的根与系数的关系 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 295.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-19 18:57:25 | ||
图片预览





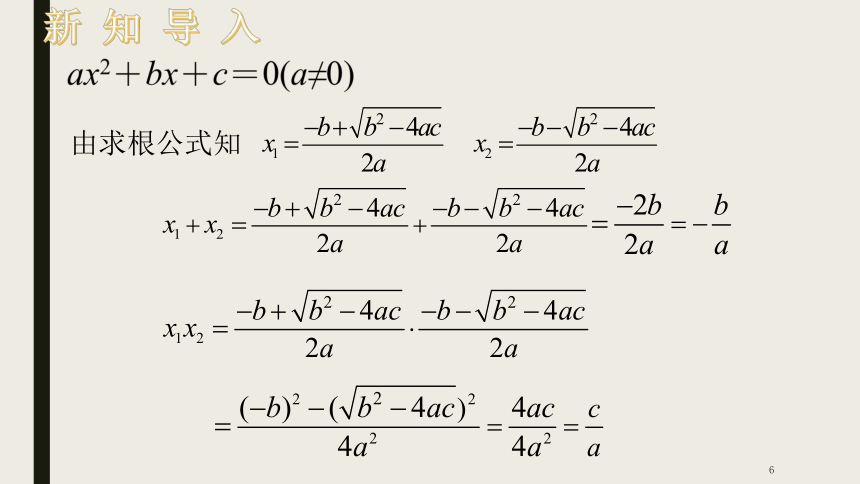

文档简介
(共15张PPT)
第二十一章
一
元
二
次
方
程
21.2.4
一元二次方程的根与系数的关系
1
学
习
目
标
1)熟练掌握一元二次方程跟与系数的关系(重点)
2)灵活运用一元二次方程跟与系数的关系解决实际问题
3)了解对跟与系数的关系的理解和推导(难点)
2
思考一:写出一元二次方程的一般式:
ax2+bx+c=0(a≠0)
对一元二次方程:
ax2
+
bx
+c
=
0(a≠0).
b2
-
4ac
>
0
时,方程有两个不相等的实数根.
b2
-
4ac
=
0
时,方程有两个相等的实数根.
b2
-
4ac
<
0
时,方程无实数根.
思考二:一元二次方程的求根公式:
思考三:如何用判别式
b2
-
4ac
来判断一元二次方程根的情况?
3
ax2+bx+c=0(a≠0)
(x-x1)(x-x2)=0
x2+px+q=0
x2-xx1-xx2-x1x2
=0
x2-(x1+x2
)
x-x1x2=0
4
方程两个根的和、积与系数分别有如下关系:
x1+x2=-p,x1x2=q.
5
由求根公式知
6
方程的两个根x1,x2和系数a,b,c有如下关系:
这表明任何一个一元二次方程的根与系数的关系为:
两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比.
7
例题:
根据一元二次方程的根与系数的关系,求下列方程两个根x1,x2的和与积:
(1)
x2-6x-15=0;
(2)
3x2+7x-9=0;
(3)
5x-1=4x2.
(1)
x1+x2=-(-6)=6,x1x2=-15.
8
随堂检测:
1.已知方程4x2+3x-2=0的两根是x1,x2,不解方程,则x1+x2=
,x1·x2=
.
2.已知关于x的方程x2+kx-2=0的一个根是1,则另一个根是
,
k的值是
.
3.已知一元二次方程2x2+bx+c=0的两个根是-1,3,则b=
,c=
.
4.若关于x的一元二次方程x2+px+q=0的两根互为相反数,则p=
;若两根互为倒数,则q=
.
9
与一元二次方程
ax2+bx+c=0(a≠0)
的两个根
x1,x2
有关的几个代数式的变形:
10
随堂检测:
不解方程,求下列方程两个根的和与积.
(1)x2-3x=15;
(2)
3x2+2=1-4x;
(3)
5x2-1=4x2+x;
(4)
2x2-x+2=3x+1.
11
随堂检测:
关于
x
的一元二次方程
x2-(a2-2a)x+a-1=0
的两个实数根互为相反数,则
a
的值为(
)
A.2
B.0
C.1
D.2或0
12
13
14
一元二次方程
ax2+bx+c=0(a≠0)
的根与系数的关系
数学语言
文字语言
一元二次方程的两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比.
使用条件
1.方程是一元二次方程,即二次项系数不为
0;
2.方程有实数根,即
Δ≥0.
重要结论
1.若一元二次方程
x2+px+q=0
的两根为
x1,x2,则
x1+x2=-p,x1x2=q.
2.以实数
x1,x2
为两根的二次项系数为1的一元二次方程是
x2-(x1+x2)x+x1x2=0.
15
第二十一章
一
元
二
次
方
程
21.2.4
一元二次方程的根与系数的关系
1
学
习
目
标
1)熟练掌握一元二次方程跟与系数的关系(重点)
2)灵活运用一元二次方程跟与系数的关系解决实际问题
3)了解对跟与系数的关系的理解和推导(难点)
2
思考一:写出一元二次方程的一般式:
ax2+bx+c=0(a≠0)
对一元二次方程:
ax2
+
bx
+c
=
0(a≠0).
b2
-
4ac
>
0
时,方程有两个不相等的实数根.
b2
-
4ac
=
0
时,方程有两个相等的实数根.
b2
-
4ac
<
0
时,方程无实数根.
思考二:一元二次方程的求根公式:
思考三:如何用判别式
b2
-
4ac
来判断一元二次方程根的情况?
3
ax2+bx+c=0(a≠0)
(x-x1)(x-x2)=0
x2+px+q=0
x2-xx1-xx2-x1x2
=0
x2-(x1+x2
)
x-x1x2=0
4
方程两个根的和、积与系数分别有如下关系:
x1+x2=-p,x1x2=q.
5
由求根公式知
6
方程的两个根x1,x2和系数a,b,c有如下关系:
这表明任何一个一元二次方程的根与系数的关系为:
两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比.
7
例题:
根据一元二次方程的根与系数的关系,求下列方程两个根x1,x2的和与积:
(1)
x2-6x-15=0;
(2)
3x2+7x-9=0;
(3)
5x-1=4x2.
(1)
x1+x2=-(-6)=6,x1x2=-15.
8
随堂检测:
1.已知方程4x2+3x-2=0的两根是x1,x2,不解方程,则x1+x2=
,x1·x2=
.
2.已知关于x的方程x2+kx-2=0的一个根是1,则另一个根是
,
k的值是
.
3.已知一元二次方程2x2+bx+c=0的两个根是-1,3,则b=
,c=
.
4.若关于x的一元二次方程x2+px+q=0的两根互为相反数,则p=
;若两根互为倒数,则q=
.
9
与一元二次方程
ax2+bx+c=0(a≠0)
的两个根
x1,x2
有关的几个代数式的变形:
10
随堂检测:
不解方程,求下列方程两个根的和与积.
(1)x2-3x=15;
(2)
3x2+2=1-4x;
(3)
5x2-1=4x2+x;
(4)
2x2-x+2=3x+1.
11
随堂检测:
关于
x
的一元二次方程
x2-(a2-2a)x+a-1=0
的两个实数根互为相反数,则
a
的值为(
)
A.2
B.0
C.1
D.2或0
12
13
14
一元二次方程
ax2+bx+c=0(a≠0)
的根与系数的关系
数学语言
文字语言
一元二次方程的两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比.
使用条件
1.方程是一元二次方程,即二次项系数不为
0;
2.方程有实数根,即
Δ≥0.
重要结论
1.若一元二次方程
x2+px+q=0
的两根为
x1,x2,则
x1+x2=-p,x1x2=q.
2.以实数
x1,x2
为两根的二次项系数为1的一元二次方程是
x2-(x1+x2)x+x1x2=0.
15
同课章节目录
