济南济北中学2019-2020学年高中物理鲁科版选修3-4:光的折射与全反射 单元测试(含解析)
文档属性
| 名称 | 济南济北中学2019-2020学年高中物理鲁科版选修3-4:光的折射与全反射 单元测试(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 397.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-07-20 06:30:02 | ||
图片预览




文档简介
光的折射与全反射
1.公园里灯光喷泉的水池中有处于同一深度的若干彩灯,在晚上观察不同颜色彩灯的深度和水面上被照亮的面积,下列说法正确的是( )
A.红灯看起来较浅,红灯照亮的水面面积较小
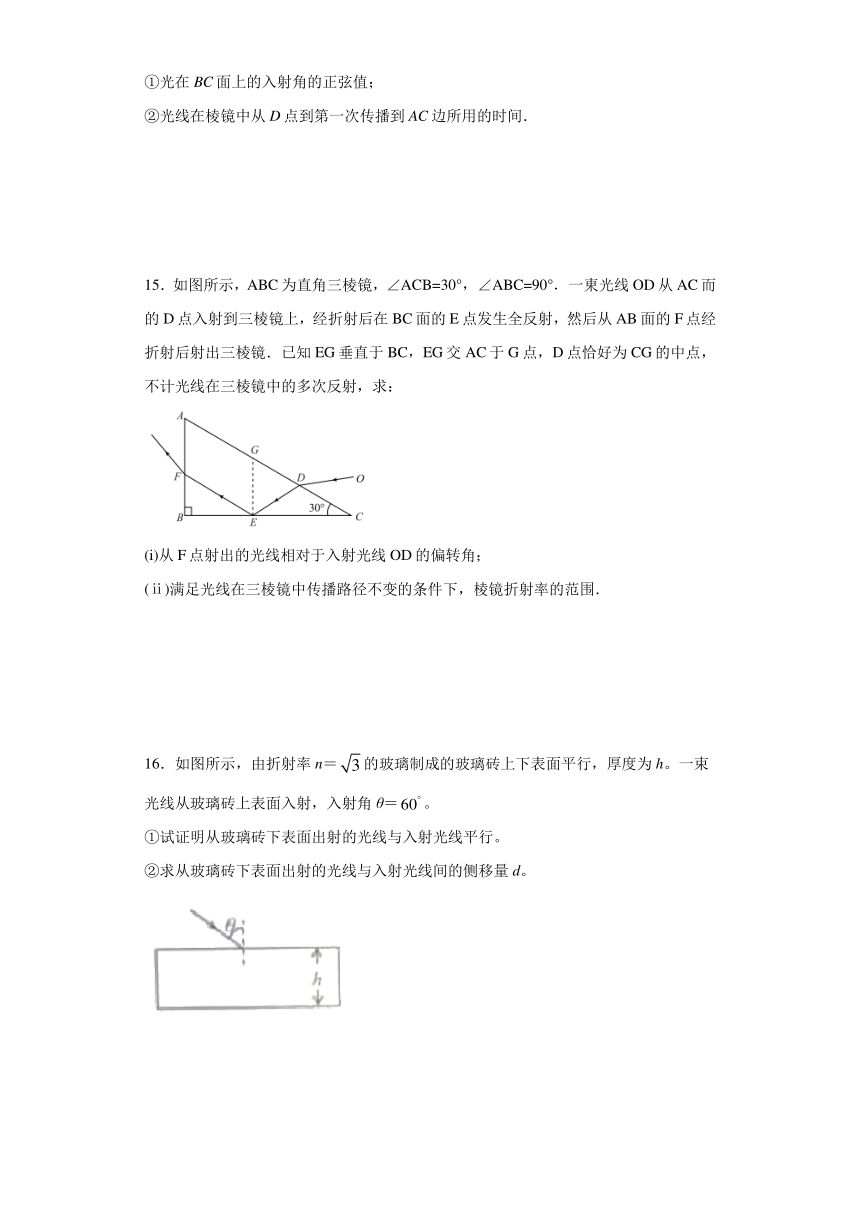
B.红灯看起来较深,红灯照亮的水面面积较小
C.红灯看起来较浅,红灯照亮的水面面积较大
D.红灯看起来较深,红灯照亮的水面面积较大
2.如图所示,一横截面为直角三角形的三棱镜,∠B=90°,∠C=30°.一束与AB面成θ=30°的光线射向AB面,经过BC边发生一次全反射,再从AC边射出,且出射光线的折射角为60°.则这种材料的折射率为( )
A. B. C. D.2
3.如图所示,一束光由空气射向半圆柱体玻璃砖,O点为该玻璃砖截面的圆心,下图中能正确描述其光路的是( )
A. B.
C. D.
4.如图,半圆形玻璃砖置于光屏PQ的左下方.一束白光沿半径方向从A点射入玻璃砖,在O点发生反射和折射,折射光在白光屏上呈现七色光带.若入射点由A向B缓慢移动,并保持白光沿半径方向入射到O点,观察到各色光在光屏上陆续消失.在光带未完全消失之前,反射光的强度变化以及光屏上最先消失的光分别是( )
A.减弱,紫光 B.减弱,红光
C.增强,紫光 D.增强,红光
5.如图所示,口径较大、充满水的薄壁圆柱形浅玻璃缸底有一发光小球,则( )
A.小球必须位于缸底中心才能从侧面看到小球
B.小球所发的光能从水面任何区域射出
C.小球所发的光从水中进入空气后频率变大
D.小球所发的光从水中进入空气后传播速度变大
6.如图所示,MN是位于竖直平面内的光屏,放在水平面上的半圆柱形玻璃砖的平面部分ab与屏平行.由光源S发出的一束白光沿半圆半径射入玻璃砖,通过圆心O再射到屏上.在水平面内以O点为圆心沿逆时针方向缓缓转动玻璃砖,在光屏上出现了彩色光带.当玻璃砖转动角度大于某一值,屏上彩色光带中的某种颜色的色光首先消失.有关彩色的排列顺序和最先消失的色光是 ( )
A.左红右紫,红光 B.左红右紫,紫光
C.左紫右红,红光 D.左紫右红,紫光
7.如图所示,放在空气中的平行玻璃砖,表面M与N平行,一束光射到表面M上,(光束不与M平行)
①如果入射角大于临界角,光在表面M即发生反射。
②无论入射角多大,光在表面M也不会发生全反射。
③可能在表面N发生全反射。
④ 由于M与N平行,光只要通过M,则不可能在表面N发生全反射。
则上述说法正确的是( )
A.①③ B.②③ C.③ D.②④
8.一束由红、蓝两单色光组成的光以入射角θ由空气射到半圆形玻璃砖表面的A处,AB是半圆的直径.进入玻璃后分为两束,分别为AC、AD,它们从A到C和从A到D的时间分别为t1和t2,则( )
A.AC是蓝光,t1小于t2 B.AC是红光,t1小于t2
C.AC是蓝光,t1等于t2 D.AC是红光,t1大于t2
9.一束光线从空气射向折射率为1.5的玻璃内,人射角为45o下面光路图中正确的是
A. B.
C. D.
10.如图所示,一细束白光由空气斜射到横截面为矩形的玻璃砖abdc的ab边上(入射光的延长线沿Od方向),则关于λ射光和折射光说法正确的是( )
A.不可能在ab界面发生全反射
B.可能射到bd面,并在bd界面发生全反射
C.一定能到达cd面,并可能在cd界面发生全反射
D.一定能到达cd面并从cd射出,射出的各种色光一定互相平行
E. 光进入玻璃砖后的速度减小
11.某同学在做完测定玻璃折射率的实验后,突发奇想,他说受到实验中光路侧移的启示,设计了一个玻璃厚度检测仪,可以用来检测玻璃厚度是否均匀,原理大致是:固定一束激光AO以不变的入射角θ1照射到MN表面,折射后从PQ面射出,最后出射光线照射到光电管C上,光电管C可将光信号转变为电信号,如图所示,依据激光束在C上移的距离,可确定玻璃管厚度的变化,若某次检测中发现光斑在C上左移了Δs,则此玻璃的厚度与原来相比变______.
12.如图所示,圆筒中有一平面镜,点光源S1发的光射到平面镜上反射到筒壁上呈光斑S2 , 当平面镜绕筒轴以角速度ω匀速转动时,光点S1在镜中的像S1′的角速度等于________ω , 光斑S2在镜中的像S2′的角速度等于________ω .
13.某种材料的三棱镜截面如图所示,∠A=90°,∠B=60°,一细光束从三棱镜AB边的中点D入射,折射光经过三棱镜BC边折射和反射后,从AC边射出的光束刚好与AC边垂直. 已知真空中的光速,AB边的长度为a=60cm,三棱镜对该细光束的折射率. 求:
①该光束从BC边射出的折射角;
②该光束从AB边射入到从AC边射出所用的时间.
14.如图所示,ABC为直角三棱镜,∠A=30°,∠B=90°,斜边AC长为L.一束单色光斜射到BC的中点D,折射光线刚好与AC平行,且折射光线照射到AB边刚好发生全反射.已知光在真空中的传播速度为c,求:
①光在BC面上的入射角的正弦值;
②光线在棱镜中从D点到第一次传播到AC边所用的时间.
15.如图所示,ABC为直角三棱镜,∠ACB=30°,∠ABC=90°.一東光线OD从AC而的D点入射到三棱镜上,经折射后在BC面的E点发生全反射,然后从AB面的F点经折射后射出三棱镜.已知EG垂直于BC,EG交AC于G点,D点恰好为CG的中点,不计光线在三棱镜中的多次反射,求:
(i)从F点射出的光线相对于入射光线OD的偏转角;
(ⅱ)满足光线在三棱镜中传播路径不变的条件下,棱镜折射率的范围.
16.如图所示,由折射率n=的玻璃制成的玻璃砖上下表面平行,厚度为h。一束光线从玻璃砖上表面入射,入射角θ=。
①试证明从玻璃砖下表面出射的光线与入射光线平行。
②求从玻璃砖下表面出射的光线与入射光线间的侧移量d。
17.如图,ΔABC是一直角三棱镜的横截面,∠A=90°,∠B=60°,一细光束从BC边的D点折射后,射到AC边的E点,发生全反射后经AB边的F点射出。EG垂直于AC交BC于G,D恰好是CG的中点。不计多次反射。
(1)假设棱镜折射率为,则光在D点的入射角为多少?
(2)为实现上述光路,棱镜折射率的取值应在什么范围?
18.如图所示,等腰直角三角形ABC为某透明介质的横截面。O为BC边的中点,位于O点处的点光源在透明介质内向各个方向发射光线,其中OD光线与OC夹角15°,从AC边上的D点射出的光线平行于BC,从E点射出的光线垂直BC向上。已知BC边长2L.求:
①该介质的折射率;
②光从O点传到E点的时间。
参考答案
1.D
【解析】
试题分析:红灯看起来较深,因为水对红光的折射率小于对绿光的折射率,根据视深与实深的关系式,折射率越小,看起来较深.由又由题意知,点光源照亮的水面边缘光线刚好发生全反射,由几何知识得,折射率越小,半径越大,
点光源照亮的水面面积为,故红灯照亮的水面面积较大,
故选D
考点:考查了折射定律的应用
点评:题关键要知道水面边缘光线刚好发生全反射,由折射定律和几何知识结合,就能轻松解答.
2.B
【解析】光路图如图所示.光线在AB面上的入射角i=90°-30°=60°,又光线从AC面上出射时的折射角i′=60°,由折射定律可知,光线在AB面上的折射角r等于在AC面上的入射角r′.
根据几何关系有:r+r′+90°+30°=180°
可得:r=30°
根据折射定律有: ,故选B.
点睛:解决光的折射定律的题目,首先要作出光路图,再根据折射定律及几何关系求解即可.
3.A
【解析】试题分析:根据折射定律垂直于射向界面的光线不发生偏折,由光疏介质射向光密介质折射角变小.
垂直射向玻璃时,光线不发生偏折,到达玻璃底面时,若入射角大于临界角则发生反射,没有折射光线.故A有可能,A正确;由空气射向玻璃,时光疏介质射向光密介质,不可能发生全反射,没有折射光线,故B错误;若光线到达玻璃的底面时入射角小于临界角则同时发生折射和反射,但应该空气中的折射角大于玻璃中的入射角,故C错误;由空气射向玻璃时,同时发生折射和反射,但应该玻璃中的折射角小于空气中的入射角,故D错误.
4.C
【解析】试题分析:光线从光密介质到光疏介质,入射角增大则反射光的强度增强;因紫色光的折射率最大,发生全反射的临界角最小,故紫光最先发生全反射,在光屏上最先消失.故选C
考点:全反射
【名师点睛】本题中应记住七色光中从红到紫,折射率增大、频率增大,而波长减小,故红光的波长最长,而紫光的频率最高,折射率最大。
5.D
【解析】
A.小球发出的光先从水中传播,然后再射入空气中,故我们从侧面就可以看到小球,选项A错误;
B.由于光从水中射入空气中,故当入射角大于临界角时,光会发生全反射,故球所发的光不是从水面任何区域都能够射出的,选项B错误;
CD.光从水中进入空气后频率不变,由于折射率变小,故光的传播速度变大,选项C错误,D正确.
6.B
【解析】
玻璃对红光的折射率最小,对紫光的折射率,入射角相同时,通过半圆柱形玻璃砖后,红光的偏折角最小,紫光的偏折角最大,则光屏上彩色光的排列顺序是左红右紫.根据临界角公式sinC=得知,紫光的临界角最小,当玻璃砖转动时,入射角增大,紫光最先发生全反射,最先从光屏上消失,故B正确,ACD错误。
7.D
【解析】①、②、B产生全反射的必要条件是光必须从光密介质射入光疏介质,可知,光从空气进入玻璃砖时,不会产生光的全反射现象,无论入射角多大,光都能从界面ab进入玻璃砖.故①错误,②正确.③、④、由于ab与cd两个表面平行,根据几何知识得知,光线在ab面上的折射角等于在cd面上的入射角,根据光路可逆原理可知,光线一定从界面cd射出,故③错误,④正确.综上选D.
【点睛】解决本题的关键是掌握全反射的条件,灵活运用光路的可逆性分析玻璃砖的光学特性.
8.C
【解析】光的偏折程度比较大,则介质对AC光的折射率比较大,AC光的频率比较大,所以AC光应是蓝光.
设AC光与法线方向成α角,AC光在介质中的传播速度为: ,则有,又,由以上两式得: ,可知,AC光与AD光的传播时间相等,故C正确,ABD错误。
9.C
【解析】光由空气射向玻璃,折射角小于入射角,反射角等于入射角,故C正确.
10.ADE
【解析】白光由空气斜射到横截面为矩形的玻璃砖abcd的ab面上,是由光疏介质射向光密介质,不可能发生全反射,故A正确;白光透过ab面后发生折射,折射角小于入射角,所以光线不可能射到bd面,故B错误;白光在ab面上发生折射,由于折射率不同,故各色光到达cd面的位置不同;但各色光在cd面的入射角都等于ab面的折射角,根据光路的可逆性,则各色光在cd面的出射角等于ab面的入射角,不可能在cd面上发生全反射,且出射光与最初的入射光平行,故C错误,D正确;根据 可知,光进入玻璃后的速度减小,选项E正确;故选ADE.
点睛:由于玻璃砖的上下表面平行,所以第一次的折射时的折射角就是第二次折射时的入射角,由折射定律可知前者的入射角与后者的折射角相等.
11.厚
【解析】
【分析】
【详解】
如图所示,虚线表示增厚以后PQ的位置,实线是原来所采用的光路图,入射角和折射角没有变化,但增厚后光斑会左移,则此玻璃的厚度与原来相比变厚;
12.2 4
【解析】
【分析】
当平面镜绕筒轴转过θ角时,则法线也转过θ角,根据反射定律判断反射光线转过的角度.
【详解】
当平面镜绕筒轴转过θ角时,则法线也转过θ角,则入射角减小θ,反射角减小θ, 因为法线也已经转过θ角,所以反射光线要旋转2θ角,故光点S1在镜中的像S1′的角速度等于2ω;即s2转动的角速度等于2ω;同理可得光斑S2在镜中的像S2′的角速度等于4ω.
【点睛】
本题主要考查学生对反射定律的掌握和理解,要求学生具有一定的空间想象能力,
13.①60°;②4.33×10-9s
【解析】
【详解】
①根据几何知识得光线在BC边的入射角i=30°
根据折射率公式,有
得
②△BDE为等边三角形,
△ECF中,
所以
光在棱镜中的传播速度
从AC边射出的光束在棱镜中传播所用的时间
得
14.①②
【解析】
【详解】
①由于折射光线DE与AC平行,因此光线在AB面上的入射角为60°,反射角也为60°.
由于折射光线DE在AB面上刚好发生全反射,则临界角C=60°
所以棱镜的折射率为:n===
???设光线在BC面的入射角为i,折射角为r,由几何关系可知r =30°
根据折射定律得:n=
可得:sini=
②由几何关系得:DE=AC=L
AE=ACcos30°=L
EF==L
光在棱镜中的传播速度为:v==
因此,光线在棱镜中从D点到第一次传播到AC边所用的时间为:t==.
15.(i) (ⅱ)
【解析】
【分析】
(i)根据几何关系得到D点折射角,从而得到E点入射角、反射角、F点入射角;再根据折射率相等得到D点入射角和F点折射角,从而求得偏角;
(ii)根据光在D、F发生折射,由折射角求得折射率的最大值;根据光在E点发生全发射,由入射角求得折射率的最小值,即可得到折射率的范围.
【详解】
(i)由于D是CG的中点,GE⊥BC,根据几何关系可得:光束在D点发生折射时的折射角为γD=30°;
那么,根据几何关系可得:在E点的入射角、反射角均为γD+30°=60°;在F点的入射角为αF=30°;
那么,设入射角为αD,可得:折射角γF=αD,故出射光相对于D点的入射光的偏角为60°-αD+γF=60°;
(ii)由E点反射角为60°可得:EF∥AC;
故根据D点折射角为γD=30°可得:棱镜折射率n≤=2;
根据光束在E点入射角为60°,发生全反射可得:,故棱镜折射率的取值范围为≤n≤2
【点睛】
光的折射率n=,故折射率越大,临界角越小;故发生全反射,入射角不小于临界角,求得折射率的下限;发生折射,折射角不大于临界角,求得折射率的上限.
16.(1)证明见解析;(2)
【解析】
【详解】
①如图所示,对于入射点O,
根据折射定律可得
对于出射点O',根据折射定律可得
因为θ2=θ3,所以θ1=θ4,则AO∥O′D,
所以入射光线与出射光线平行
②由折射定律可得 ,计算得出θ2=30°
如图所示d=OO'sin(θ1﹣θ2)
解得:。
17.(1)60°(2)
【解析】
【详解】
(1)设i1和r1分别是该光线在BC面上的入射角和折射角,i2和r2分别是该光线在AC面上的入射角和反射角,i3和r3分别是该光线在AB面上的入射角和折射角。则由几何关系得i2=r2=60°,r1=i3=30°于是光线在BC面上折射时由折射定律有:
sini1=nsinr1= 所以 i1=60°
(2)光线在AC面上发生全反射,光线在AB面上不发生全反射,于是有:
nsini2≥nsinC>nsini3
式中C是全反射临界角,满足nsinC=1
由此可知,棱镜的折射率n的取值范围应为
18.
【解析】
【详解】
光路图如图所示:
①做出法线,由几何关系知从D射出的光线的折射角r=45°
入射角i=30°,根据折射定律得:
②过E点做法线,由几何关系得:α=r=45°
由折射定律得:β=i=30°
由几何关系得:∠OED=60°,∠EDO=60°,△ODE为等边三角形,即OE=OD,
在△ODC中由正弦定理得解得:
光在介质中的传播速度 光在介质中的传播时间 联立解得:
1.公园里灯光喷泉的水池中有处于同一深度的若干彩灯,在晚上观察不同颜色彩灯的深度和水面上被照亮的面积,下列说法正确的是( )
A.红灯看起来较浅,红灯照亮的水面面积较小
B.红灯看起来较深,红灯照亮的水面面积较小
C.红灯看起来较浅,红灯照亮的水面面积较大
D.红灯看起来较深,红灯照亮的水面面积较大
2.如图所示,一横截面为直角三角形的三棱镜,∠B=90°,∠C=30°.一束与AB面成θ=30°的光线射向AB面,经过BC边发生一次全反射,再从AC边射出,且出射光线的折射角为60°.则这种材料的折射率为( )
A. B. C. D.2
3.如图所示,一束光由空气射向半圆柱体玻璃砖,O点为该玻璃砖截面的圆心,下图中能正确描述其光路的是( )
A. B.
C. D.
4.如图,半圆形玻璃砖置于光屏PQ的左下方.一束白光沿半径方向从A点射入玻璃砖,在O点发生反射和折射,折射光在白光屏上呈现七色光带.若入射点由A向B缓慢移动,并保持白光沿半径方向入射到O点,观察到各色光在光屏上陆续消失.在光带未完全消失之前,反射光的强度变化以及光屏上最先消失的光分别是( )
A.减弱,紫光 B.减弱,红光
C.增强,紫光 D.增强,红光
5.如图所示,口径较大、充满水的薄壁圆柱形浅玻璃缸底有一发光小球,则( )
A.小球必须位于缸底中心才能从侧面看到小球
B.小球所发的光能从水面任何区域射出
C.小球所发的光从水中进入空气后频率变大
D.小球所发的光从水中进入空气后传播速度变大
6.如图所示,MN是位于竖直平面内的光屏,放在水平面上的半圆柱形玻璃砖的平面部分ab与屏平行.由光源S发出的一束白光沿半圆半径射入玻璃砖,通过圆心O再射到屏上.在水平面内以O点为圆心沿逆时针方向缓缓转动玻璃砖,在光屏上出现了彩色光带.当玻璃砖转动角度大于某一值,屏上彩色光带中的某种颜色的色光首先消失.有关彩色的排列顺序和最先消失的色光是 ( )
A.左红右紫,红光 B.左红右紫,紫光
C.左紫右红,红光 D.左紫右红,紫光
7.如图所示,放在空气中的平行玻璃砖,表面M与N平行,一束光射到表面M上,(光束不与M平行)
①如果入射角大于临界角,光在表面M即发生反射。
②无论入射角多大,光在表面M也不会发生全反射。
③可能在表面N发生全反射。
④ 由于M与N平行,光只要通过M,则不可能在表面N发生全反射。
则上述说法正确的是( )
A.①③ B.②③ C.③ D.②④
8.一束由红、蓝两单色光组成的光以入射角θ由空气射到半圆形玻璃砖表面的A处,AB是半圆的直径.进入玻璃后分为两束,分别为AC、AD,它们从A到C和从A到D的时间分别为t1和t2,则( )
A.AC是蓝光,t1小于t2 B.AC是红光,t1小于t2
C.AC是蓝光,t1等于t2 D.AC是红光,t1大于t2
9.一束光线从空气射向折射率为1.5的玻璃内,人射角为45o下面光路图中正确的是
A. B.
C. D.
10.如图所示,一细束白光由空气斜射到横截面为矩形的玻璃砖abdc的ab边上(入射光的延长线沿Od方向),则关于λ射光和折射光说法正确的是( )
A.不可能在ab界面发生全反射
B.可能射到bd面,并在bd界面发生全反射
C.一定能到达cd面,并可能在cd界面发生全反射
D.一定能到达cd面并从cd射出,射出的各种色光一定互相平行
E. 光进入玻璃砖后的速度减小
11.某同学在做完测定玻璃折射率的实验后,突发奇想,他说受到实验中光路侧移的启示,设计了一个玻璃厚度检测仪,可以用来检测玻璃厚度是否均匀,原理大致是:固定一束激光AO以不变的入射角θ1照射到MN表面,折射后从PQ面射出,最后出射光线照射到光电管C上,光电管C可将光信号转变为电信号,如图所示,依据激光束在C上移的距离,可确定玻璃管厚度的变化,若某次检测中发现光斑在C上左移了Δs,则此玻璃的厚度与原来相比变______.
12.如图所示,圆筒中有一平面镜,点光源S1发的光射到平面镜上反射到筒壁上呈光斑S2 , 当平面镜绕筒轴以角速度ω匀速转动时,光点S1在镜中的像S1′的角速度等于________ω , 光斑S2在镜中的像S2′的角速度等于________ω .
13.某种材料的三棱镜截面如图所示,∠A=90°,∠B=60°,一细光束从三棱镜AB边的中点D入射,折射光经过三棱镜BC边折射和反射后,从AC边射出的光束刚好与AC边垂直. 已知真空中的光速,AB边的长度为a=60cm,三棱镜对该细光束的折射率. 求:
①该光束从BC边射出的折射角;
②该光束从AB边射入到从AC边射出所用的时间.
14.如图所示,ABC为直角三棱镜,∠A=30°,∠B=90°,斜边AC长为L.一束单色光斜射到BC的中点D,折射光线刚好与AC平行,且折射光线照射到AB边刚好发生全反射.已知光在真空中的传播速度为c,求:
①光在BC面上的入射角的正弦值;
②光线在棱镜中从D点到第一次传播到AC边所用的时间.
15.如图所示,ABC为直角三棱镜,∠ACB=30°,∠ABC=90°.一東光线OD从AC而的D点入射到三棱镜上,经折射后在BC面的E点发生全反射,然后从AB面的F点经折射后射出三棱镜.已知EG垂直于BC,EG交AC于G点,D点恰好为CG的中点,不计光线在三棱镜中的多次反射,求:
(i)从F点射出的光线相对于入射光线OD的偏转角;
(ⅱ)满足光线在三棱镜中传播路径不变的条件下,棱镜折射率的范围.
16.如图所示,由折射率n=的玻璃制成的玻璃砖上下表面平行,厚度为h。一束光线从玻璃砖上表面入射,入射角θ=。
①试证明从玻璃砖下表面出射的光线与入射光线平行。
②求从玻璃砖下表面出射的光线与入射光线间的侧移量d。
17.如图,ΔABC是一直角三棱镜的横截面,∠A=90°,∠B=60°,一细光束从BC边的D点折射后,射到AC边的E点,发生全反射后经AB边的F点射出。EG垂直于AC交BC于G,D恰好是CG的中点。不计多次反射。
(1)假设棱镜折射率为,则光在D点的入射角为多少?
(2)为实现上述光路,棱镜折射率的取值应在什么范围?
18.如图所示,等腰直角三角形ABC为某透明介质的横截面。O为BC边的中点,位于O点处的点光源在透明介质内向各个方向发射光线,其中OD光线与OC夹角15°,从AC边上的D点射出的光线平行于BC,从E点射出的光线垂直BC向上。已知BC边长2L.求:
①该介质的折射率;
②光从O点传到E点的时间。
参考答案
1.D
【解析】
试题分析:红灯看起来较深,因为水对红光的折射率小于对绿光的折射率,根据视深与实深的关系式,折射率越小,看起来较深.由又由题意知,点光源照亮的水面边缘光线刚好发生全反射,由几何知识得,折射率越小,半径越大,
点光源照亮的水面面积为,故红灯照亮的水面面积较大,
故选D
考点:考查了折射定律的应用
点评:题关键要知道水面边缘光线刚好发生全反射,由折射定律和几何知识结合,就能轻松解答.
2.B
【解析】光路图如图所示.光线在AB面上的入射角i=90°-30°=60°,又光线从AC面上出射时的折射角i′=60°,由折射定律可知,光线在AB面上的折射角r等于在AC面上的入射角r′.
根据几何关系有:r+r′+90°+30°=180°
可得:r=30°
根据折射定律有: ,故选B.
点睛:解决光的折射定律的题目,首先要作出光路图,再根据折射定律及几何关系求解即可.
3.A
【解析】试题分析:根据折射定律垂直于射向界面的光线不发生偏折,由光疏介质射向光密介质折射角变小.
垂直射向玻璃时,光线不发生偏折,到达玻璃底面时,若入射角大于临界角则发生反射,没有折射光线.故A有可能,A正确;由空气射向玻璃,时光疏介质射向光密介质,不可能发生全反射,没有折射光线,故B错误;若光线到达玻璃的底面时入射角小于临界角则同时发生折射和反射,但应该空气中的折射角大于玻璃中的入射角,故C错误;由空气射向玻璃时,同时发生折射和反射,但应该玻璃中的折射角小于空气中的入射角,故D错误.
4.C
【解析】试题分析:光线从光密介质到光疏介质,入射角增大则反射光的强度增强;因紫色光的折射率最大,发生全反射的临界角最小,故紫光最先发生全反射,在光屏上最先消失.故选C
考点:全反射
【名师点睛】本题中应记住七色光中从红到紫,折射率增大、频率增大,而波长减小,故红光的波长最长,而紫光的频率最高,折射率最大。
5.D
【解析】
A.小球发出的光先从水中传播,然后再射入空气中,故我们从侧面就可以看到小球,选项A错误;
B.由于光从水中射入空气中,故当入射角大于临界角时,光会发生全反射,故球所发的光不是从水面任何区域都能够射出的,选项B错误;
CD.光从水中进入空气后频率不变,由于折射率变小,故光的传播速度变大,选项C错误,D正确.
6.B
【解析】
玻璃对红光的折射率最小,对紫光的折射率,入射角相同时,通过半圆柱形玻璃砖后,红光的偏折角最小,紫光的偏折角最大,则光屏上彩色光的排列顺序是左红右紫.根据临界角公式sinC=得知,紫光的临界角最小,当玻璃砖转动时,入射角增大,紫光最先发生全反射,最先从光屏上消失,故B正确,ACD错误。
7.D
【解析】①、②、B产生全反射的必要条件是光必须从光密介质射入光疏介质,可知,光从空气进入玻璃砖时,不会产生光的全反射现象,无论入射角多大,光都能从界面ab进入玻璃砖.故①错误,②正确.③、④、由于ab与cd两个表面平行,根据几何知识得知,光线在ab面上的折射角等于在cd面上的入射角,根据光路可逆原理可知,光线一定从界面cd射出,故③错误,④正确.综上选D.
【点睛】解决本题的关键是掌握全反射的条件,灵活运用光路的可逆性分析玻璃砖的光学特性.
8.C
【解析】光的偏折程度比较大,则介质对AC光的折射率比较大,AC光的频率比较大,所以AC光应是蓝光.
设AC光与法线方向成α角,AC光在介质中的传播速度为: ,则有,又,由以上两式得: ,可知,AC光与AD光的传播时间相等,故C正确,ABD错误。
9.C
【解析】光由空气射向玻璃,折射角小于入射角,反射角等于入射角,故C正确.
10.ADE
【解析】白光由空气斜射到横截面为矩形的玻璃砖abcd的ab面上,是由光疏介质射向光密介质,不可能发生全反射,故A正确;白光透过ab面后发生折射,折射角小于入射角,所以光线不可能射到bd面,故B错误;白光在ab面上发生折射,由于折射率不同,故各色光到达cd面的位置不同;但各色光在cd面的入射角都等于ab面的折射角,根据光路的可逆性,则各色光在cd面的出射角等于ab面的入射角,不可能在cd面上发生全反射,且出射光与最初的入射光平行,故C错误,D正确;根据 可知,光进入玻璃后的速度减小,选项E正确;故选ADE.
点睛:由于玻璃砖的上下表面平行,所以第一次的折射时的折射角就是第二次折射时的入射角,由折射定律可知前者的入射角与后者的折射角相等.
11.厚
【解析】
【分析】
【详解】
如图所示,虚线表示增厚以后PQ的位置,实线是原来所采用的光路图,入射角和折射角没有变化,但增厚后光斑会左移,则此玻璃的厚度与原来相比变厚;
12.2 4
【解析】
【分析】
当平面镜绕筒轴转过θ角时,则法线也转过θ角,根据反射定律判断反射光线转过的角度.
【详解】
当平面镜绕筒轴转过θ角时,则法线也转过θ角,则入射角减小θ,反射角减小θ, 因为法线也已经转过θ角,所以反射光线要旋转2θ角,故光点S1在镜中的像S1′的角速度等于2ω;即s2转动的角速度等于2ω;同理可得光斑S2在镜中的像S2′的角速度等于4ω.
【点睛】
本题主要考查学生对反射定律的掌握和理解,要求学生具有一定的空间想象能力,
13.①60°;②4.33×10-9s
【解析】
【详解】
①根据几何知识得光线在BC边的入射角i=30°
根据折射率公式,有
得
②△BDE为等边三角形,
△ECF中,
所以
光在棱镜中的传播速度
从AC边射出的光束在棱镜中传播所用的时间
得
14.①②
【解析】
【详解】
①由于折射光线DE与AC平行,因此光线在AB面上的入射角为60°,反射角也为60°.
由于折射光线DE在AB面上刚好发生全反射,则临界角C=60°
所以棱镜的折射率为:n===
???设光线在BC面的入射角为i,折射角为r,由几何关系可知r =30°
根据折射定律得:n=
可得:sini=
②由几何关系得:DE=AC=L
AE=ACcos30°=L
EF==L
光在棱镜中的传播速度为:v==
因此,光线在棱镜中从D点到第一次传播到AC边所用的时间为:t==.
15.(i) (ⅱ)
【解析】
【分析】
(i)根据几何关系得到D点折射角,从而得到E点入射角、反射角、F点入射角;再根据折射率相等得到D点入射角和F点折射角,从而求得偏角;
(ii)根据光在D、F发生折射,由折射角求得折射率的最大值;根据光在E点发生全发射,由入射角求得折射率的最小值,即可得到折射率的范围.
【详解】
(i)由于D是CG的中点,GE⊥BC,根据几何关系可得:光束在D点发生折射时的折射角为γD=30°;
那么,根据几何关系可得:在E点的入射角、反射角均为γD+30°=60°;在F点的入射角为αF=30°;
那么,设入射角为αD,可得:折射角γF=αD,故出射光相对于D点的入射光的偏角为60°-αD+γF=60°;
(ii)由E点反射角为60°可得:EF∥AC;
故根据D点折射角为γD=30°可得:棱镜折射率n≤=2;
根据光束在E点入射角为60°,发生全反射可得:,故棱镜折射率的取值范围为≤n≤2
【点睛】
光的折射率n=,故折射率越大,临界角越小;故发生全反射,入射角不小于临界角,求得折射率的下限;发生折射,折射角不大于临界角,求得折射率的上限.
16.(1)证明见解析;(2)
【解析】
【详解】
①如图所示,对于入射点O,
根据折射定律可得
对于出射点O',根据折射定律可得
因为θ2=θ3,所以θ1=θ4,则AO∥O′D,
所以入射光线与出射光线平行
②由折射定律可得 ,计算得出θ2=30°
如图所示d=OO'sin(θ1﹣θ2)
解得:。
17.(1)60°(2)
【解析】
【详解】
(1)设i1和r1分别是该光线在BC面上的入射角和折射角,i2和r2分别是该光线在AC面上的入射角和反射角,i3和r3分别是该光线在AB面上的入射角和折射角。则由几何关系得i2=r2=60°,r1=i3=30°于是光线在BC面上折射时由折射定律有:
sini1=nsinr1= 所以 i1=60°
(2)光线在AC面上发生全反射,光线在AB面上不发生全反射,于是有:
nsini2≥nsinC>nsini3
式中C是全反射临界角,满足nsinC=1
由此可知,棱镜的折射率n的取值范围应为
18.
【解析】
【详解】
光路图如图所示:
①做出法线,由几何关系知从D射出的光线的折射角r=45°
入射角i=30°,根据折射定律得:
②过E点做法线,由几何关系得:α=r=45°
由折射定律得:β=i=30°
由几何关系得:∠OED=60°,∠EDO=60°,△ODE为等边三角形,即OE=OD,
在△ODC中由正弦定理得解得:
光在介质中的传播速度 光在介质中的传播时间 联立解得:
同课章节目录
- 第1章 机械振动
- 导 入 从我国古代的“鱼洗”说起
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 生活中的振动
- 第2章 机械波
- 导 入 身边的波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第3章 电磁波
- 导 入 无处不在的电磁波
- 第1节 电磁波的产生
- 第2节 电磁波的发射、传播和接收
- 第3节 电磁波的应用及防护
- 专题探究 振动与波的实验与调研
- 第4章 光的折射与全反射
- 导 入 美妙的彩虹
- 第1节 光的折射定律
- 第2节 光的全反射
- 第3节 光导纤维及其应用
- 第5章 光的干涉 衍射 偏振
- 导 入 从五彩斑斓的肥皂泡说起
- 第1节 光的干涉
- 第2节 光的衍射
- 第3节 光的偏振
- 第4节 激光与全息照相
- 专题探究 光学部分的实验与调研
- 第6章 相对论与天体物理
- 导 入 从双生子佯谬谈起
- 第1节 牛顿眼中的世界
- 第2节 爱因斯坦眼中的世界
- 第3节 广义相对论初步
- 第4节 探索宇宙
