2019-2020学年黑龙江省大庆市肇源县六年级下学期期末数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2019-2020学年黑龙江省大庆市肇源县六年级下学期期末数学试卷(五四学制)(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 859.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-20 00:00:00 | ||
图片预览



文档简介
2019-2020学年六年级(下)期末数学试卷(五四学制)
一、选择题(共10小题).
1.计算﹣5的绝对值是( )
A.5 B. C.﹣5 D.0.5
2.下列各组两项中,是同类项的是( )
A.xy与﹣xy B.
C.﹣2xy与﹣3ab D.3x2y与3xy2
3.如图是一无盖的正方体盒子,下列展开图不能叠合成无盖正方体的是( )
A. B.
C. D.
4.湿地旅游爱好者小明了解到鄂东南某市水资源总量为42.43亿立方米,其中42.43亿用科学记数法可表示为( )
A.42.43×109 B.4.423×108 C.4.243×109 D.0.423×108
5.某种商品的标价为120元,若以九折降价出售,相对于进货价仍获利20%,该商品的进货价为( )
A.80元 B.85元 C.90元 D.95元
6.已知线段AB,画出它的中点C,再画出BC的中点D,再画出AD的中点E,再画出AE的中点F,那么AF等于AB的( )
A. B. C. D.
7.4点10分,时针与分针所夹的小于平角的角为( )
A.55° B.65°
C.70° D.以上结论都不对
8.如图,从A到B有①,②,③三条路线,最短的路线是①,其理由是( )
A.因为它最直 B.两点确定一条直线
C.两点间的距离的概念 D.两点之间,线段最短
9.某校九年级学生总人数为500,其男女生所占比例如图所示,则该校九年级男生人数为( )
A.48 B.52 C.240 D.260
10.如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=30°,下列结论错误的是( )
A.∠ACD=120° B.∠ACD=∠BCE
C.∠ACE=120° D.∠ACE﹣∠BCD=120°
二、填空题(每题3分,满分30分)
11.已知x=3是方程ax﹣6=a+10的解,则a= .
12.点C在射线AB上,若AB=3,BC=2,则AC为 .
13.如图,AB:BC:CD=2:3:4,AB的中点M与CD的中点N的距离是3cm,则BC= .
14.如图,OA⊥OB,∠BOC=30°,OD平分∠AOC,则∠BOD= 度.
15.已知代数式x+2y的值是3,则代数式2x+4y+1的值是 .
16.对于有理数a、b,定义一种新运算,规定a☆b=a2﹣|b|,则3☆(﹣2)= .
17.已知|x|=3,|y|=7,且 xy<0,则 x+y的值等于 .
18.当x=1时,代数式x2﹣2x+a的值为3,则当x=﹣1时,代数式x2﹣2x+a= .
19.填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m的值是 .
20.如图,化简代数式|a+b|﹣|a﹣1|+|b﹣2|的结果是 .
三、解答题(本大题共9小题,共60分)
21.计算与化简:
(1)12﹣(﹣6)+(﹣9);
(2)(﹣48)×(﹣﹣+);
(3)﹣32÷(﹣2)2×|﹣1|×6+(﹣2)3.
22.先化简,再求值:已知|x+3|+(y﹣)2=0,求代数式﹣2x2﹣2[3y2﹣2(x2﹣y2)+6]的值.
23.解下列方程:
(1)4﹣3(2﹣x)=5x;
(2).
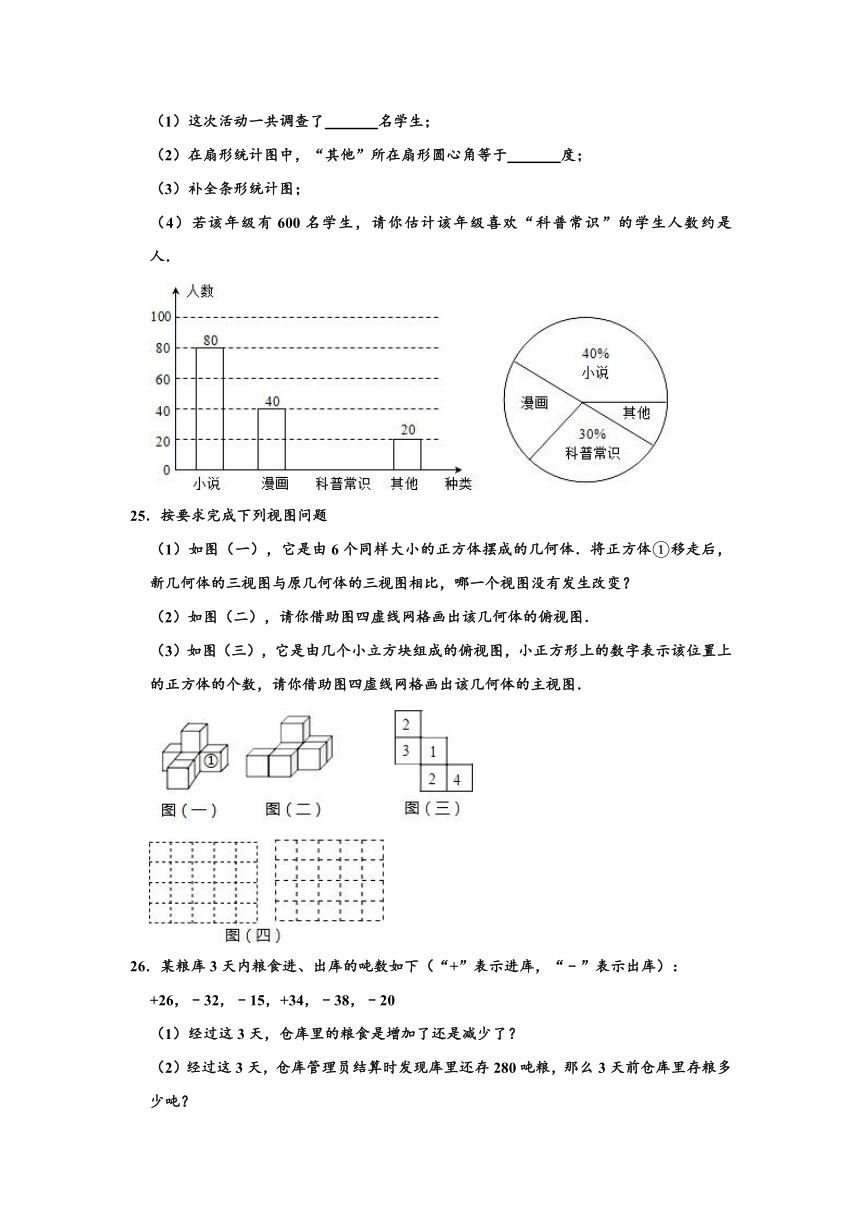
24.某校为了了解本校八年级学生课外阅读的喜好,随机抽取该校八年级部分学生进行问卷调査(每人只选一种书籍).如图是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:
(1)这次活动一共调查了 名学生;
(2)在扇形统计图中,“其他”所在扇形圆心角等于 度;
(3)补全条形统计图;
(4)若该年级有600名学生,请你估计该年级喜欢“科普常识”的学生人数约是 人.
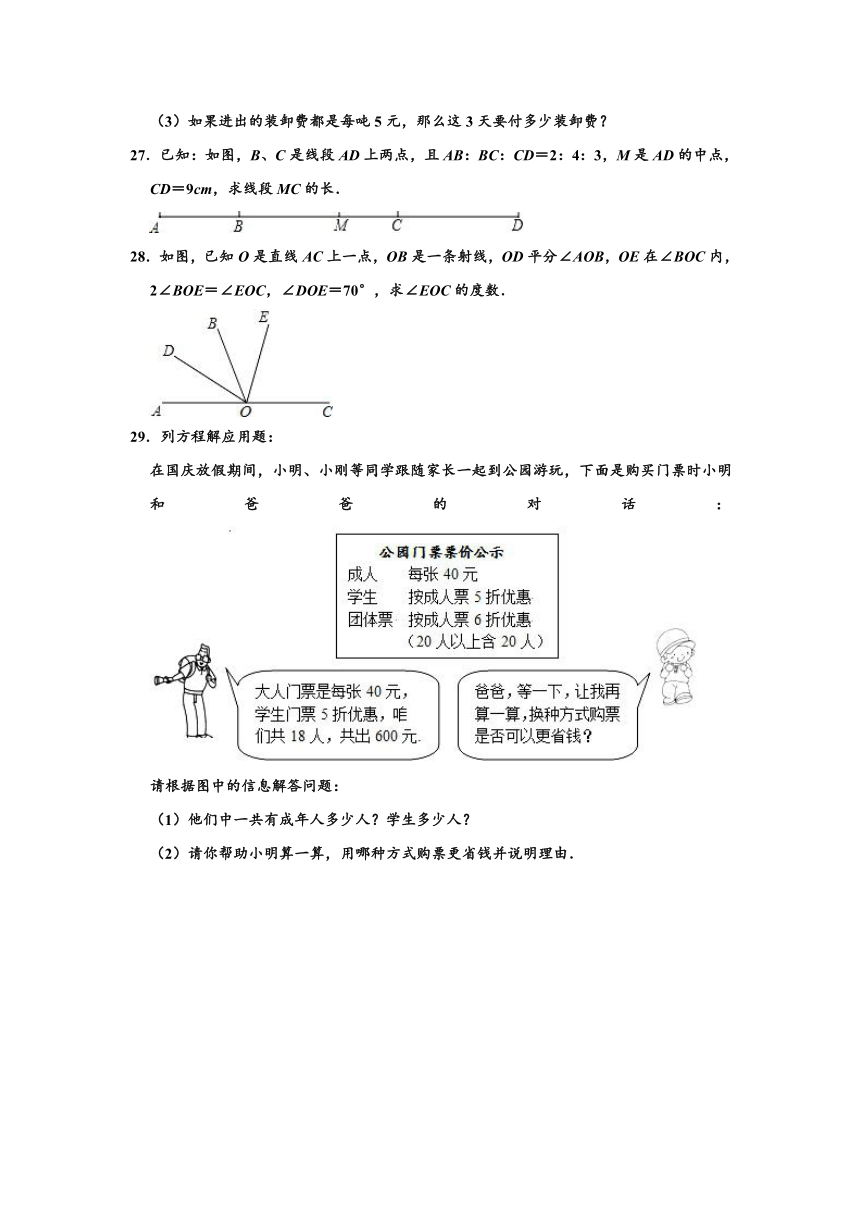
25.按要求完成下列视图问题
(1)如图(一),它是由6个同样大小的正方体摆成的几何体.将正方体①移走后,新几何体的三视图与原几何体的三视图相比,哪一个视图没有发生改变?
(2)如图(二),请你借助图四虚线网格画出该几何体的俯视图.
(3)如图(三),它是由几个小立方块组成的俯视图,小正方形上的数字表示该位置上的正方体的个数,请你借助图四虚线网格画出该几何体的主视图.
26.某粮库3天内粮食进、出库的吨数如下(“+”表示进库,“﹣”表示出库):
+26,﹣32,﹣15,+34,﹣38,﹣20
(1)经过这3天,仓库里的粮食是增加了还是减少了?
(2)经过这3天,仓库管理员结算时发现库里还存280吨粮,那么3天前仓库里存粮多少吨?
(3)如果进出的装卸费都是每吨5元,那么这3天要付多少装卸费?
27.已知:如图,B、C是线段AD上两点,且AB:BC:CD=2:4:3,M是AD的中点,CD=9cm,求线段MC的长.
28.如图,已知O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,2∠BOE=∠EOC,∠DOE=70°,求∠EOC的度数.
29.列方程解应用题:
在国庆放假期间,小明、小刚等同学跟随家长一起到公园游玩,下面是购买门票时小明和爸爸的对话:
请根据图中的信息解答问题:
(1)他们中一共有成年人多少人?学生多少人?
(2)请你帮助小明算一算,用哪种方式购票更省钱并说明理由.
参考答案
一、选择题(共10小题,每小题3分,满分30分.在毎小题所给出的四个选项中,只有一项是符合题目要求的.)
1.计算﹣5的绝对值是( )
A.5 B. C.﹣5 D.0.5
【分析】根据绝对值的性质:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
解:根据负数的绝对值是它的相反数,得|﹣5|=5.
故选:A.
2.下列各组两项中,是同类项的是( )
A.xy与﹣xy B.
C.﹣2xy与﹣3ab D.3x2y与3xy2
【分析】根据同类项的定义(所含字母相同,并且相同字母的指数也相等的项,叫同类项)判断即可.
解:A、是同类项,故本选项正确;
B、不是同类项,故本选项错误;
C、不是同类项,故本选项错误;
D、不是同类项,故本选项错误;
故选:A.
3.如图是一无盖的正方体盒子,下列展开图不能叠合成无盖正方体的是( )
A. B.
C. D.
【分析】根据正方体展开图的性质,可得答案.
解:C中有两个正方形重合,无法叠合成无盖正方体,故C错误;
故选:C.
4.湿地旅游爱好者小明了解到鄂东南某市水资源总量为42.43亿立方米,其中42.43亿用科学记数法可表示为( )
A.42.43×109 B.4.423×108 C.4.243×109 D.0.423×108
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
解:根据42.43亿=4243000000,用科学记数法表示为:4.243×109.
故选:C.
5.某种商品的标价为120元,若以九折降价出售,相对于进货价仍获利20%,该商品的进货价为( )
A.80元 B.85元 C.90元 D.95元
【分析】商品的实际售价是标价×90%=进货价+所得利润(20%?x).设该商品的进货价为x元,根据题意列方程得x+20%?x=120×90%,解这个方程即可求出进货价.
解:设该商品的进货价为x元,
根据题意列方程得x+20%?x=120×90%,
解得x=90.
故选:C.
6.已知线段AB,画出它的中点C,再画出BC的中点D,再画出AD的中点E,再画出AE的中点F,那么AF等于AB的( )
A. B. C. D.
【分析】根据题意AF=AE=AD,那么只需求出AD、AB的关系即可;因为AD=AB﹣BD,而BD=BC=AB,由此求得AF、AB的比例关系.
解:由题意可作出下图:
结合上图和题意可知:
AF=AE=AD;
而AD=AB﹣BD=AB﹣BC=AB﹣AB=AB,
∴AF=AD=×AB=AB,
故选:D.
7.4点10分,时针与分针所夹的小于平角的角为( )
A.55° B.65°
C.70° D.以上结论都不对
【分析】因为钟表上的刻度是把一个圆平均分成了12等份,每一份是30°,找出4点10分时针和分针分别转动角度即可求出.
解:∵4点10分时,分针在指在2时位置处,时针指在4时过10分钟处,由于一大格是30°,10分钟转过的角度为=5°,因此4点10分时,分针与时针的夹角是2×30°+5°=65°.
故选:B.
8.如图,从A到B有①,②,③三条路线,最短的路线是①,其理由是( )
A.因为它最直 B.两点确定一条直线
C.两点间的距离的概念 D.两点之间,线段最短
【分析】根据线段的性质进行解答即可.
解:从A到B有①,②,③三条路线,最短的路线是①,其理由是:两点之间,线段最短,
故选:D.
9.某校九年级学生总人数为500,其男女生所占比例如图所示,则该校九年级男生人数为( )
A.48 B.52 C.240 D.260
【分析】利用该校九年级男生人数所占的百分比,乘以总人数,即可求出该校九年级男生人数.
解:500×52%=260人,故选D.
10.如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=30°,下列结论错误的是( )
A.∠ACD=120° B.∠ACD=∠BCE
C.∠ACE=120° D.∠ACE﹣∠BCD=120°
【分析】依据题意题意可知∠ACB=∠DCE=90°,然后依据图形间角的和差关系求解即可.
解:A、∵∠ACB=90°,∠BCD=30°,∴∠ACD=∠ACB+∠BCD=120°,故A与要求不符;
B、∵∠DCE=90°,∠BCD=30°,∴∠BCE=∠DCE+∠BCD=120°,∴∠ACD=∠BCE,故B与要求不符;
C、∵∠ACE=360°﹣90°﹣90°﹣30°=150°,故C错误,与要求相符;
D、∵∠ACE﹣∠BCD=150°﹣30°=120°,故D与要求不符.
故选:C.
二、填空题(每题3分,满分30分)
11.已知x=3是方程ax﹣6=a+10的解,则a= 8 .
【分析】将x=3代入方程ax﹣6=a+10,然后解关于a的一元一次方程即可.
解:∵x=3是方程ax﹣6=a+10的解,
∴x=3满足方程ax﹣6=a+10,
∴3a﹣6=a+10,
解得a=8.
故答案为:8.
12.点C在射线AB上,若AB=3,BC=2,则AC为 1或5 .
【分析】分为两种情况,化成图形,根据图形和已知求出即可.
解:当C在线段AB上时,
AC=AB﹣BC=3﹣2=1,
当C在线段AB的延长线时,
AC=AB+BC=3+2=5,
即AC=1或5,
故答案为:1或5.
13.如图,AB:BC:CD=2:3:4,AB的中点M与CD的中点N的距离是3cm,则BC= 1.5cm .
【分析】设AB=2xcm,BC=3xcm,CD=4xcm,求出MB=xcm,CN=2xcm,得出方程x+3x+2x=3,求出即可.
解:设AB=2xcm,BC=3xcm,CD=4xcm,
∵M是AB的中点,N是CD的中点,
∴MB=xcm,CN=2xcm,
∴MB+BC+CN=x+3x+2x=3,
∴x=0.5,
∴3x=1.5,
即BC=1.5cm.
故答案为:1.5cm.
14.如图,OA⊥OB,∠BOC=30°,OD平分∠AOC,则∠BOD= 30 度.
【分析】利用余角和角的平分线的定义计算.
解:OA⊥OB,∠AOB=90°,即∠AOD+BOD=90°;
∵OD平分∠AOC,
∴∠AOD=∠DOC,即∠BOD+∠BOC+BOD=90°,
即2∠BOD+∠BOC=90°
∵∠BOC=30°,
∴∠BOD=30°.
故填30.
15.已知代数式x+2y的值是3,则代数式2x+4y+1的值是 7 .
【分析】把题中的代数式2x+4y+1变为x+2y的形式,再直接代入求解.
解:∵x+2y=3,
∴2x+4y+1=2(x+2y)+1
=2×3+1=7.
故答案为:7.
16.对于有理数a、b,定义一种新运算,规定a☆b=a2﹣|b|,则3☆(﹣2)= 7 .
【分析】根据新定义把新运算转化为常规运算进行解答便可.
解:3☆(﹣2)=32﹣|﹣2|=9﹣2=7,
故答案为:7.
17.已知|x|=3,|y|=7,且 xy<0,则 x+y的值等于 ±4 .
【分析】根据绝对值的意义得到x=±3,y=±7,由xy<0,则x=3,y=﹣7或x=﹣3,y=7,然后把它们分别代入x+y中计算即可.
解:∵|x|=3,|y|=7,
∴x=±3,y=±7,
而 xy<0,
∴x=3,y=﹣7或x=﹣3,y=7,
当x=3,y=﹣7时,x+y=3﹣7=﹣4;
当x=﹣3,y=7时,x+y=﹣3+7=4.
故答案为±4.
18.当x=1时,代数式x2﹣2x+a的值为3,则当x=﹣1时,代数式x2﹣2x+a= 7 .
【分析】将x=1代入代数式求出a的值,将x=﹣1及a的值代入计算即可求出值.
解:∵当x=1时,x2﹣2x+a=3,
∴1﹣2+a=3,即a=4,
∴当x=﹣1时,x2﹣2x+a=(﹣1)2﹣2×(﹣1)+4=7.
故答案为:7.
19.填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m的值是 74 .
【分析】观察四个正方形,可得到规律,每个正方形中左下角的数比左上角的数大2、右上角的数比左上角的数大4,右下角的数=对角线上两个数的乘积﹣左上角的数,依此计算即可求解.
解:m=8×10﹣6
=80﹣6
=74.
故答案为:74.
20.如图,化简代数式|a+b|﹣|a﹣1|+|b﹣2|的结果是 3 .
【分析】根据数轴上点的位置判断出绝对值里边式子的正负,利用绝对值的代数意义化简,即可得到结果.
解:由数轴可知﹣1<b<0,1<a<2,
所以a+b>0,a﹣1>0,b﹣2<0,
则|a+b|﹣|a﹣1|+|b﹣2|=a+b﹣(a﹣1)﹣(b﹣2)=a+b﹣a+1﹣b+2=3.
故答案为:3.
三、解答题(本大题共9小题,共60分)
21.计算与化简:
(1)12﹣(﹣6)+(﹣9);
(2)(﹣48)×(﹣﹣+);
(3)﹣32÷(﹣2)2×|﹣1|×6+(﹣2)3.
【分析】根据有理数的混合运算顺序和运算法则进行计算便可.
解:(1)12﹣(﹣6)+(﹣9)
=12+6+(﹣9)
=18+(﹣9)
=9;
(2)(﹣48)×(﹣﹣+)
=(﹣48)×(﹣)+(﹣48)×(﹣)+(﹣48)×
=24+30﹣28
=26;
(3)﹣32÷(﹣2)2×|﹣1|×6+(﹣2)3.
=﹣9÷4××6+(﹣8)
=﹣××6+(﹣8)
=(﹣18)+(﹣8)
=﹣26.
22.先化简,再求值:已知|x+3|+(y﹣)2=0,求代数式﹣2x2﹣2[3y2﹣2(x2﹣y2)+6]的值.
【分析】直接利用偶次方的性质以及绝对值的性质分别化简得出x,y的值,进而利用整式的加减运算法则化简得出答案.
解:因为|x+3|≥0且(y﹣)2≥0,|x+3|+(y﹣)2=0,
所以|x+3|=0且(y﹣)2=0,
所以x+3=0且y﹣=0,
所以x=﹣3且y=,
﹣2x2﹣2[3y2﹣2(x2﹣y2)+6]
=﹣2x2﹣2[3y2﹣2x2+2y2+6]
=﹣2x2﹣2[5y2﹣2x2+6]
=﹣2x2﹣10y2+4x2﹣12
=2x2﹣10y2﹣12
=2×(﹣3)2﹣10×()2﹣12
=3.5.
23.解下列方程:
(1)4﹣3(2﹣x)=5x;
(2).
【分析】(1)方程去括号,移项合并,将x系数化为1,即可求出解;
(2)方程去分母,去括号,移项合并,将x系数化为1,即可求出解.
解:(1)去括号得:4﹣6+3x=5x,
移项合并得:2x=﹣2,
解得:x=﹣1;
(2)去分母得:4x﹣2=3x+6+6,
移项合并得:x=14.
24.某校为了了解本校八年级学生课外阅读的喜好,随机抽取该校八年级部分学生进行问卷调査(每人只选一种书籍).如图是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:
(1)这次活动一共调查了 200 名学生;
(2)在扇形统计图中,“其他”所在扇形圆心角等于 36 度;
(3)补全条形统计图;
(4)若该年级有600名学生,请你估计该年级喜欢“科普常识”的学生人数约是 180 人.
【分析】(1)根据条形图可知阅读小说的有80人,根据在扇形图中所占比例得出调查学生数;
(2)根据条形图可知阅读其他的有20人,根据总人数可求出它在扇形图中所占比例;
(3)求出第3组人数画出图形即可;
(4)根据科普常识的学生所占比例,即可估计全校人数.
解:(1)80÷40%=200人,
(2)20÷200×360°=36°,
(3)200×30%=60(人),如图所示:
(4)600×30%=180人,
故答案为:(1)200,(2)36,(4)180.
25.按要求完成下列视图问题
(1)如图(一),它是由6个同样大小的正方体摆成的几何体.将正方体①移走后,新几何体的三视图与原几何体的三视图相比,哪一个视图没有发生改变?
(2)如图(二),请你借助图四虚线网格画出该几何体的俯视图.
(3)如图(三),它是由几个小立方块组成的俯视图,小正方形上的数字表示该位置上的正方体的个数,请你借助图四虚线网格画出该几何体的主视图.
【分析】(1)利用结合体的形状,结合三视图可得出左视图没有发生变化;
(2)利用几何体的形状结合俯视图的得出得出答案;
(3)利用小立方体的个数结合俯视图得出主视图即可.
解:(1)如图(一),它是由6个同样大小的正方体摆成的几何体.将正方体①移走后,
新几何体的三视图与原几何体的三视图相比,左视图没有发生改变;
(2)如图1所示,
(3)如图2所示.
26.某粮库3天内粮食进、出库的吨数如下(“+”表示进库,“﹣”表示出库):
+26,﹣32,﹣15,+34,﹣38,﹣20
(1)经过这3天,仓库里的粮食是增加了还是减少了?
(2)经过这3天,仓库管理员结算时发现库里还存280吨粮,那么3天前仓库里存粮多少吨?
(3)如果进出的装卸费都是每吨5元,那么这3天要付多少装卸费?
【分析】(1)根据有理数的加法,可得答案;
(2)根据剩余的加上减少的45吨,可得答案;
(3)根据单位费用乘以数量,可得答案.
解:(1)26+(﹣32)+(﹣15)+34+(﹣38)+(﹣20)=﹣45吨,
答:库里的粮食是减少了45吨;
(2)280+45=325吨,
答:3天前库里有粮325吨;
(3)(26+|﹣32|+|﹣15|+34+|﹣38|+|﹣20|)×5=165×5=825元,
答:这3天要付825元装卸费.
27.已知:如图,B、C是线段AD上两点,且AB:BC:CD=2:4:3,M是AD的中点,CD=9cm,求线段MC的长.
【分析】根据比例关系求得AB=6cm,BC=12cm,则AD=27cm,然后由线段中点的性质来求MD的长度,则MC=MD﹣CD.
解:∵AB:BC:CD=2:4:3,
∴设AB=2xcm,BC=4xcm,CD=3xcm,
∴3x=9,
解得 x=3,
∴AB=6cm,BC=12cm,
∴AD=AB+BC+CD=6+12+9=27(cm),
又∵点M是AD的中点,
∴MD=AD=13.5(cm),
∴MC=13.5﹣9=4.5(cm).
28.如图,已知O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,2∠BOE=∠EOC,∠DOE=70°,求∠EOC的度数.
【分析】先设∠AOB为x,∠BOC为(180﹣x)°,根据角平分线的定义、∠BOE与∠EOC的关系建立方程解答即可.
解:设∠AOB为x,则∠BOC为(180﹣x)°,
∵OD平分∠AOB,
∴∠DOB=∠AOB,
则可得∠DOB=x,
∵2∠BOE=∠EOC,
∴∠BOE=∠BOC=,
∵∠DOE=∠DOB+∠BOE=70°
则可得:,
解得x=60°,
∴∠BOC=180°﹣60°=120°,
∴∠EOC==80°.
29.列方程解应用题:
在国庆放假期间,小明、小刚等同学跟随家长一起到公园游玩,下面是购买门票时小明和爸爸的对话:
请根据图中的信息解答问题:
(1)他们中一共有成年人多少人?学生多少人?
(2)请你帮助小明算一算,用哪种方式购票更省钱并说明理由.
【分析】(1)设他们中一共有成年人x人,那么学生有(18﹣x)人,根据总价=单价×数量,即可得出关于x的一元一次方程,解之即可得出结论;
(2)先求出购买20张团体票的总价钱,比较后即可得出结论.
解:(1)设他们中一共有成年人x人,那么学生有(18﹣x)人,
根据题意得:40x+40×0.5×(18﹣x)=600,
解得:x=12,
∴18﹣x=18﹣12=6.
答:他们中一共有成年人12人,学生6人.
(2)40×0.6×20=480(元),
∵480<600,
∴按照团体票的优惠方案购买20张门票更省钱,能节省120元钱.
一、选择题(共10小题).
1.计算﹣5的绝对值是( )
A.5 B. C.﹣5 D.0.5
2.下列各组两项中,是同类项的是( )
A.xy与﹣xy B.
C.﹣2xy与﹣3ab D.3x2y与3xy2
3.如图是一无盖的正方体盒子,下列展开图不能叠合成无盖正方体的是( )
A. B.
C. D.
4.湿地旅游爱好者小明了解到鄂东南某市水资源总量为42.43亿立方米,其中42.43亿用科学记数法可表示为( )
A.42.43×109 B.4.423×108 C.4.243×109 D.0.423×108
5.某种商品的标价为120元,若以九折降价出售,相对于进货价仍获利20%,该商品的进货价为( )
A.80元 B.85元 C.90元 D.95元
6.已知线段AB,画出它的中点C,再画出BC的中点D,再画出AD的中点E,再画出AE的中点F,那么AF等于AB的( )
A. B. C. D.
7.4点10分,时针与分针所夹的小于平角的角为( )
A.55° B.65°
C.70° D.以上结论都不对
8.如图,从A到B有①,②,③三条路线,最短的路线是①,其理由是( )
A.因为它最直 B.两点确定一条直线
C.两点间的距离的概念 D.两点之间,线段最短
9.某校九年级学生总人数为500,其男女生所占比例如图所示,则该校九年级男生人数为( )
A.48 B.52 C.240 D.260
10.如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=30°,下列结论错误的是( )
A.∠ACD=120° B.∠ACD=∠BCE
C.∠ACE=120° D.∠ACE﹣∠BCD=120°
二、填空题(每题3分,满分30分)
11.已知x=3是方程ax﹣6=a+10的解,则a= .
12.点C在射线AB上,若AB=3,BC=2,则AC为 .
13.如图,AB:BC:CD=2:3:4,AB的中点M与CD的中点N的距离是3cm,则BC= .
14.如图,OA⊥OB,∠BOC=30°,OD平分∠AOC,则∠BOD= 度.
15.已知代数式x+2y的值是3,则代数式2x+4y+1的值是 .
16.对于有理数a、b,定义一种新运算,规定a☆b=a2﹣|b|,则3☆(﹣2)= .
17.已知|x|=3,|y|=7,且 xy<0,则 x+y的值等于 .
18.当x=1时,代数式x2﹣2x+a的值为3,则当x=﹣1时,代数式x2﹣2x+a= .
19.填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m的值是 .
20.如图,化简代数式|a+b|﹣|a﹣1|+|b﹣2|的结果是 .
三、解答题(本大题共9小题,共60分)
21.计算与化简:
(1)12﹣(﹣6)+(﹣9);
(2)(﹣48)×(﹣﹣+);
(3)﹣32÷(﹣2)2×|﹣1|×6+(﹣2)3.
22.先化简,再求值:已知|x+3|+(y﹣)2=0,求代数式﹣2x2﹣2[3y2﹣2(x2﹣y2)+6]的值.
23.解下列方程:
(1)4﹣3(2﹣x)=5x;
(2).
24.某校为了了解本校八年级学生课外阅读的喜好,随机抽取该校八年级部分学生进行问卷调査(每人只选一种书籍).如图是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:
(1)这次活动一共调查了 名学生;
(2)在扇形统计图中,“其他”所在扇形圆心角等于 度;
(3)补全条形统计图;
(4)若该年级有600名学生,请你估计该年级喜欢“科普常识”的学生人数约是 人.
25.按要求完成下列视图问题
(1)如图(一),它是由6个同样大小的正方体摆成的几何体.将正方体①移走后,新几何体的三视图与原几何体的三视图相比,哪一个视图没有发生改变?
(2)如图(二),请你借助图四虚线网格画出该几何体的俯视图.
(3)如图(三),它是由几个小立方块组成的俯视图,小正方形上的数字表示该位置上的正方体的个数,请你借助图四虚线网格画出该几何体的主视图.
26.某粮库3天内粮食进、出库的吨数如下(“+”表示进库,“﹣”表示出库):
+26,﹣32,﹣15,+34,﹣38,﹣20
(1)经过这3天,仓库里的粮食是增加了还是减少了?
(2)经过这3天,仓库管理员结算时发现库里还存280吨粮,那么3天前仓库里存粮多少吨?
(3)如果进出的装卸费都是每吨5元,那么这3天要付多少装卸费?
27.已知:如图,B、C是线段AD上两点,且AB:BC:CD=2:4:3,M是AD的中点,CD=9cm,求线段MC的长.
28.如图,已知O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,2∠BOE=∠EOC,∠DOE=70°,求∠EOC的度数.
29.列方程解应用题:
在国庆放假期间,小明、小刚等同学跟随家长一起到公园游玩,下面是购买门票时小明和爸爸的对话:
请根据图中的信息解答问题:
(1)他们中一共有成年人多少人?学生多少人?
(2)请你帮助小明算一算,用哪种方式购票更省钱并说明理由.
参考答案
一、选择题(共10小题,每小题3分,满分30分.在毎小题所给出的四个选项中,只有一项是符合题目要求的.)
1.计算﹣5的绝对值是( )
A.5 B. C.﹣5 D.0.5
【分析】根据绝对值的性质:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
解:根据负数的绝对值是它的相反数,得|﹣5|=5.
故选:A.
2.下列各组两项中,是同类项的是( )
A.xy与﹣xy B.
C.﹣2xy与﹣3ab D.3x2y与3xy2
【分析】根据同类项的定义(所含字母相同,并且相同字母的指数也相等的项,叫同类项)判断即可.
解:A、是同类项,故本选项正确;
B、不是同类项,故本选项错误;
C、不是同类项,故本选项错误;
D、不是同类项,故本选项错误;
故选:A.
3.如图是一无盖的正方体盒子,下列展开图不能叠合成无盖正方体的是( )
A. B.
C. D.
【分析】根据正方体展开图的性质,可得答案.
解:C中有两个正方形重合,无法叠合成无盖正方体,故C错误;
故选:C.
4.湿地旅游爱好者小明了解到鄂东南某市水资源总量为42.43亿立方米,其中42.43亿用科学记数法可表示为( )
A.42.43×109 B.4.423×108 C.4.243×109 D.0.423×108
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
解:根据42.43亿=4243000000,用科学记数法表示为:4.243×109.
故选:C.
5.某种商品的标价为120元,若以九折降价出售,相对于进货价仍获利20%,该商品的进货价为( )
A.80元 B.85元 C.90元 D.95元
【分析】商品的实际售价是标价×90%=进货价+所得利润(20%?x).设该商品的进货价为x元,根据题意列方程得x+20%?x=120×90%,解这个方程即可求出进货价.
解:设该商品的进货价为x元,
根据题意列方程得x+20%?x=120×90%,
解得x=90.
故选:C.
6.已知线段AB,画出它的中点C,再画出BC的中点D,再画出AD的中点E,再画出AE的中点F,那么AF等于AB的( )
A. B. C. D.
【分析】根据题意AF=AE=AD,那么只需求出AD、AB的关系即可;因为AD=AB﹣BD,而BD=BC=AB,由此求得AF、AB的比例关系.
解:由题意可作出下图:
结合上图和题意可知:
AF=AE=AD;
而AD=AB﹣BD=AB﹣BC=AB﹣AB=AB,
∴AF=AD=×AB=AB,
故选:D.
7.4点10分,时针与分针所夹的小于平角的角为( )
A.55° B.65°
C.70° D.以上结论都不对
【分析】因为钟表上的刻度是把一个圆平均分成了12等份,每一份是30°,找出4点10分时针和分针分别转动角度即可求出.
解:∵4点10分时,分针在指在2时位置处,时针指在4时过10分钟处,由于一大格是30°,10分钟转过的角度为=5°,因此4点10分时,分针与时针的夹角是2×30°+5°=65°.
故选:B.
8.如图,从A到B有①,②,③三条路线,最短的路线是①,其理由是( )
A.因为它最直 B.两点确定一条直线
C.两点间的距离的概念 D.两点之间,线段最短
【分析】根据线段的性质进行解答即可.
解:从A到B有①,②,③三条路线,最短的路线是①,其理由是:两点之间,线段最短,
故选:D.
9.某校九年级学生总人数为500,其男女生所占比例如图所示,则该校九年级男生人数为( )
A.48 B.52 C.240 D.260
【分析】利用该校九年级男生人数所占的百分比,乘以总人数,即可求出该校九年级男生人数.
解:500×52%=260人,故选D.
10.如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=30°,下列结论错误的是( )
A.∠ACD=120° B.∠ACD=∠BCE
C.∠ACE=120° D.∠ACE﹣∠BCD=120°
【分析】依据题意题意可知∠ACB=∠DCE=90°,然后依据图形间角的和差关系求解即可.
解:A、∵∠ACB=90°,∠BCD=30°,∴∠ACD=∠ACB+∠BCD=120°,故A与要求不符;
B、∵∠DCE=90°,∠BCD=30°,∴∠BCE=∠DCE+∠BCD=120°,∴∠ACD=∠BCE,故B与要求不符;
C、∵∠ACE=360°﹣90°﹣90°﹣30°=150°,故C错误,与要求相符;
D、∵∠ACE﹣∠BCD=150°﹣30°=120°,故D与要求不符.
故选:C.
二、填空题(每题3分,满分30分)
11.已知x=3是方程ax﹣6=a+10的解,则a= 8 .
【分析】将x=3代入方程ax﹣6=a+10,然后解关于a的一元一次方程即可.
解:∵x=3是方程ax﹣6=a+10的解,
∴x=3满足方程ax﹣6=a+10,
∴3a﹣6=a+10,
解得a=8.
故答案为:8.
12.点C在射线AB上,若AB=3,BC=2,则AC为 1或5 .
【分析】分为两种情况,化成图形,根据图形和已知求出即可.
解:当C在线段AB上时,
AC=AB﹣BC=3﹣2=1,
当C在线段AB的延长线时,
AC=AB+BC=3+2=5,
即AC=1或5,
故答案为:1或5.
13.如图,AB:BC:CD=2:3:4,AB的中点M与CD的中点N的距离是3cm,则BC= 1.5cm .
【分析】设AB=2xcm,BC=3xcm,CD=4xcm,求出MB=xcm,CN=2xcm,得出方程x+3x+2x=3,求出即可.
解:设AB=2xcm,BC=3xcm,CD=4xcm,
∵M是AB的中点,N是CD的中点,
∴MB=xcm,CN=2xcm,
∴MB+BC+CN=x+3x+2x=3,
∴x=0.5,
∴3x=1.5,
即BC=1.5cm.
故答案为:1.5cm.
14.如图,OA⊥OB,∠BOC=30°,OD平分∠AOC,则∠BOD= 30 度.
【分析】利用余角和角的平分线的定义计算.
解:OA⊥OB,∠AOB=90°,即∠AOD+BOD=90°;
∵OD平分∠AOC,
∴∠AOD=∠DOC,即∠BOD+∠BOC+BOD=90°,
即2∠BOD+∠BOC=90°
∵∠BOC=30°,
∴∠BOD=30°.
故填30.
15.已知代数式x+2y的值是3,则代数式2x+4y+1的值是 7 .
【分析】把题中的代数式2x+4y+1变为x+2y的形式,再直接代入求解.
解:∵x+2y=3,
∴2x+4y+1=2(x+2y)+1
=2×3+1=7.
故答案为:7.
16.对于有理数a、b,定义一种新运算,规定a☆b=a2﹣|b|,则3☆(﹣2)= 7 .
【分析】根据新定义把新运算转化为常规运算进行解答便可.
解:3☆(﹣2)=32﹣|﹣2|=9﹣2=7,
故答案为:7.
17.已知|x|=3,|y|=7,且 xy<0,则 x+y的值等于 ±4 .
【分析】根据绝对值的意义得到x=±3,y=±7,由xy<0,则x=3,y=﹣7或x=﹣3,y=7,然后把它们分别代入x+y中计算即可.
解:∵|x|=3,|y|=7,
∴x=±3,y=±7,
而 xy<0,
∴x=3,y=﹣7或x=﹣3,y=7,
当x=3,y=﹣7时,x+y=3﹣7=﹣4;
当x=﹣3,y=7时,x+y=﹣3+7=4.
故答案为±4.
18.当x=1时,代数式x2﹣2x+a的值为3,则当x=﹣1时,代数式x2﹣2x+a= 7 .
【分析】将x=1代入代数式求出a的值,将x=﹣1及a的值代入计算即可求出值.
解:∵当x=1时,x2﹣2x+a=3,
∴1﹣2+a=3,即a=4,
∴当x=﹣1时,x2﹣2x+a=(﹣1)2﹣2×(﹣1)+4=7.
故答案为:7.
19.填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m的值是 74 .
【分析】观察四个正方形,可得到规律,每个正方形中左下角的数比左上角的数大2、右上角的数比左上角的数大4,右下角的数=对角线上两个数的乘积﹣左上角的数,依此计算即可求解.
解:m=8×10﹣6
=80﹣6
=74.
故答案为:74.
20.如图,化简代数式|a+b|﹣|a﹣1|+|b﹣2|的结果是 3 .
【分析】根据数轴上点的位置判断出绝对值里边式子的正负,利用绝对值的代数意义化简,即可得到结果.
解:由数轴可知﹣1<b<0,1<a<2,
所以a+b>0,a﹣1>0,b﹣2<0,
则|a+b|﹣|a﹣1|+|b﹣2|=a+b﹣(a﹣1)﹣(b﹣2)=a+b﹣a+1﹣b+2=3.
故答案为:3.
三、解答题(本大题共9小题,共60分)
21.计算与化简:
(1)12﹣(﹣6)+(﹣9);
(2)(﹣48)×(﹣﹣+);
(3)﹣32÷(﹣2)2×|﹣1|×6+(﹣2)3.
【分析】根据有理数的混合运算顺序和运算法则进行计算便可.
解:(1)12﹣(﹣6)+(﹣9)
=12+6+(﹣9)
=18+(﹣9)
=9;
(2)(﹣48)×(﹣﹣+)
=(﹣48)×(﹣)+(﹣48)×(﹣)+(﹣48)×
=24+30﹣28
=26;
(3)﹣32÷(﹣2)2×|﹣1|×6+(﹣2)3.
=﹣9÷4××6+(﹣8)
=﹣××6+(﹣8)
=(﹣18)+(﹣8)
=﹣26.
22.先化简,再求值:已知|x+3|+(y﹣)2=0,求代数式﹣2x2﹣2[3y2﹣2(x2﹣y2)+6]的值.
【分析】直接利用偶次方的性质以及绝对值的性质分别化简得出x,y的值,进而利用整式的加减运算法则化简得出答案.
解:因为|x+3|≥0且(y﹣)2≥0,|x+3|+(y﹣)2=0,
所以|x+3|=0且(y﹣)2=0,
所以x+3=0且y﹣=0,
所以x=﹣3且y=,
﹣2x2﹣2[3y2﹣2(x2﹣y2)+6]
=﹣2x2﹣2[3y2﹣2x2+2y2+6]
=﹣2x2﹣2[5y2﹣2x2+6]
=﹣2x2﹣10y2+4x2﹣12
=2x2﹣10y2﹣12
=2×(﹣3)2﹣10×()2﹣12
=3.5.
23.解下列方程:
(1)4﹣3(2﹣x)=5x;
(2).
【分析】(1)方程去括号,移项合并,将x系数化为1,即可求出解;
(2)方程去分母,去括号,移项合并,将x系数化为1,即可求出解.
解:(1)去括号得:4﹣6+3x=5x,
移项合并得:2x=﹣2,
解得:x=﹣1;
(2)去分母得:4x﹣2=3x+6+6,
移项合并得:x=14.
24.某校为了了解本校八年级学生课外阅读的喜好,随机抽取该校八年级部分学生进行问卷调査(每人只选一种书籍).如图是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:
(1)这次活动一共调查了 200 名学生;
(2)在扇形统计图中,“其他”所在扇形圆心角等于 36 度;
(3)补全条形统计图;
(4)若该年级有600名学生,请你估计该年级喜欢“科普常识”的学生人数约是 180 人.
【分析】(1)根据条形图可知阅读小说的有80人,根据在扇形图中所占比例得出调查学生数;
(2)根据条形图可知阅读其他的有20人,根据总人数可求出它在扇形图中所占比例;
(3)求出第3组人数画出图形即可;
(4)根据科普常识的学生所占比例,即可估计全校人数.
解:(1)80÷40%=200人,
(2)20÷200×360°=36°,
(3)200×30%=60(人),如图所示:
(4)600×30%=180人,
故答案为:(1)200,(2)36,(4)180.
25.按要求完成下列视图问题
(1)如图(一),它是由6个同样大小的正方体摆成的几何体.将正方体①移走后,新几何体的三视图与原几何体的三视图相比,哪一个视图没有发生改变?
(2)如图(二),请你借助图四虚线网格画出该几何体的俯视图.
(3)如图(三),它是由几个小立方块组成的俯视图,小正方形上的数字表示该位置上的正方体的个数,请你借助图四虚线网格画出该几何体的主视图.
【分析】(1)利用结合体的形状,结合三视图可得出左视图没有发生变化;
(2)利用几何体的形状结合俯视图的得出得出答案;
(3)利用小立方体的个数结合俯视图得出主视图即可.
解:(1)如图(一),它是由6个同样大小的正方体摆成的几何体.将正方体①移走后,
新几何体的三视图与原几何体的三视图相比,左视图没有发生改变;
(2)如图1所示,
(3)如图2所示.
26.某粮库3天内粮食进、出库的吨数如下(“+”表示进库,“﹣”表示出库):
+26,﹣32,﹣15,+34,﹣38,﹣20
(1)经过这3天,仓库里的粮食是增加了还是减少了?
(2)经过这3天,仓库管理员结算时发现库里还存280吨粮,那么3天前仓库里存粮多少吨?
(3)如果进出的装卸费都是每吨5元,那么这3天要付多少装卸费?
【分析】(1)根据有理数的加法,可得答案;
(2)根据剩余的加上减少的45吨,可得答案;
(3)根据单位费用乘以数量,可得答案.
解:(1)26+(﹣32)+(﹣15)+34+(﹣38)+(﹣20)=﹣45吨,
答:库里的粮食是减少了45吨;
(2)280+45=325吨,
答:3天前库里有粮325吨;
(3)(26+|﹣32|+|﹣15|+34+|﹣38|+|﹣20|)×5=165×5=825元,
答:这3天要付825元装卸费.
27.已知:如图,B、C是线段AD上两点,且AB:BC:CD=2:4:3,M是AD的中点,CD=9cm,求线段MC的长.
【分析】根据比例关系求得AB=6cm,BC=12cm,则AD=27cm,然后由线段中点的性质来求MD的长度,则MC=MD﹣CD.
解:∵AB:BC:CD=2:4:3,
∴设AB=2xcm,BC=4xcm,CD=3xcm,
∴3x=9,
解得 x=3,
∴AB=6cm,BC=12cm,
∴AD=AB+BC+CD=6+12+9=27(cm),
又∵点M是AD的中点,
∴MD=AD=13.5(cm),
∴MC=13.5﹣9=4.5(cm).
28.如图,已知O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,2∠BOE=∠EOC,∠DOE=70°,求∠EOC的度数.
【分析】先设∠AOB为x,∠BOC为(180﹣x)°,根据角平分线的定义、∠BOE与∠EOC的关系建立方程解答即可.
解:设∠AOB为x,则∠BOC为(180﹣x)°,
∵OD平分∠AOB,
∴∠DOB=∠AOB,
则可得∠DOB=x,
∵2∠BOE=∠EOC,
∴∠BOE=∠BOC=,
∵∠DOE=∠DOB+∠BOE=70°
则可得:,
解得x=60°,
∴∠BOC=180°﹣60°=120°,
∴∠EOC==80°.
29.列方程解应用题:
在国庆放假期间,小明、小刚等同学跟随家长一起到公园游玩,下面是购买门票时小明和爸爸的对话:
请根据图中的信息解答问题:
(1)他们中一共有成年人多少人?学生多少人?
(2)请你帮助小明算一算,用哪种方式购票更省钱并说明理由.
【分析】(1)设他们中一共有成年人x人,那么学生有(18﹣x)人,根据总价=单价×数量,即可得出关于x的一元一次方程,解之即可得出结论;
(2)先求出购买20张团体票的总价钱,比较后即可得出结论.
解:(1)设他们中一共有成年人x人,那么学生有(18﹣x)人,
根据题意得:40x+40×0.5×(18﹣x)=600,
解得:x=12,
∴18﹣x=18﹣12=6.
答:他们中一共有成年人12人,学生6人.
(2)40×0.6×20=480(元),
∵480<600,
∴按照团体票的优惠方案购买20张门票更省钱,能节省120元钱.
同课章节目录
