4.1单位圆与任意角的正弦函数、余弦函数的定义课件
文档属性
| 名称 | 4.1单位圆与任意角的正弦函数、余弦函数的定义课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 948.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-20 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
4.1
单位圆与任意角的正弦函数、
余弦函数的定义
问题
引航
1.单位圆中是如何定义正、余弦函数的?正、余弦函数的定义域是什么?
2.正、余弦函数在各个象限的符号如何确定?
3.任意角的三角函数的定义是什么?
锐角的正弦、余弦函数的定义:
对边
邻边
斜边
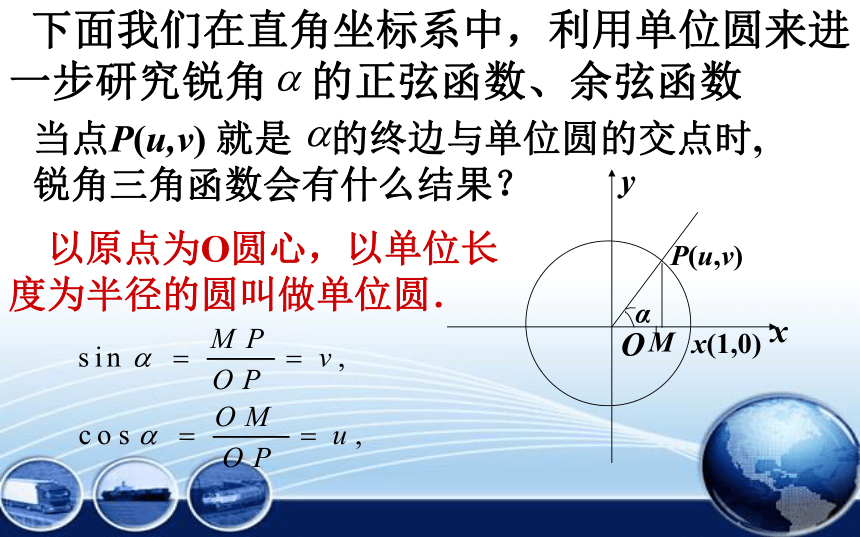
以原点为O圆心,以单位长度为半径的圆叫做单位圆.
x(1,0)
O
P(u,v)
α
y
M
x
当点P(u,v)
就是
的终边与单位圆的交点时,锐角三角函数会有什么结果?
下面我们在直角坐标系中,利用单位圆来进一步研究锐角
的正弦函数、余弦函数
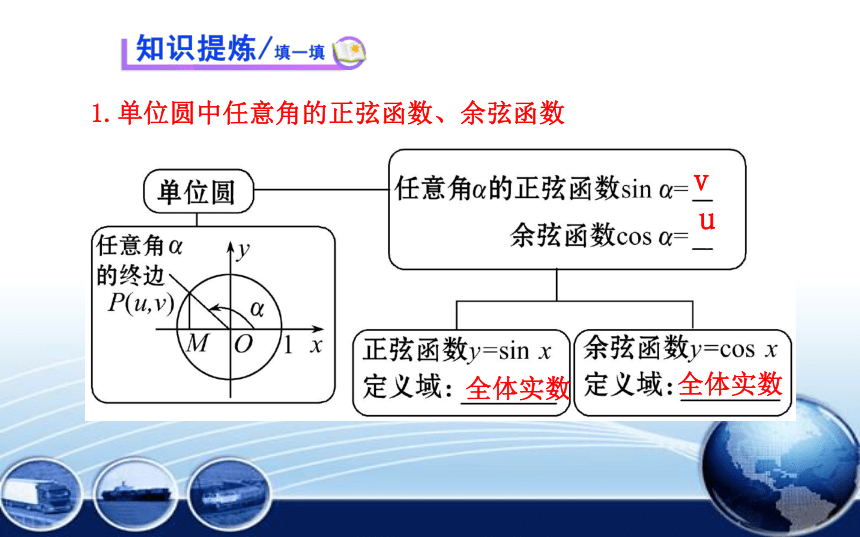
任意角的正弦函数、余弦函数定义:
x
y
O
P(u,v)
α
A(1,0)
(1)v叫做α的正弦,记作sinα,
即sinα=v;
(2)u叫做α的余弦,记作
cosα,即cosα=u
如图,设α是一个任意角,它的终边与单位圆交于点P(u,v),那么:
三角函数
都是以角为自变量,以单位圆上的点的坐标(比值)为函数值的函数.
角(弧度数)
实数
三角函数可以看成是自变量为实数的函数
一一对应
定义域
函数
1.单位圆中任意角的正弦函数、余弦函数
v
u
全体实数
全体实数
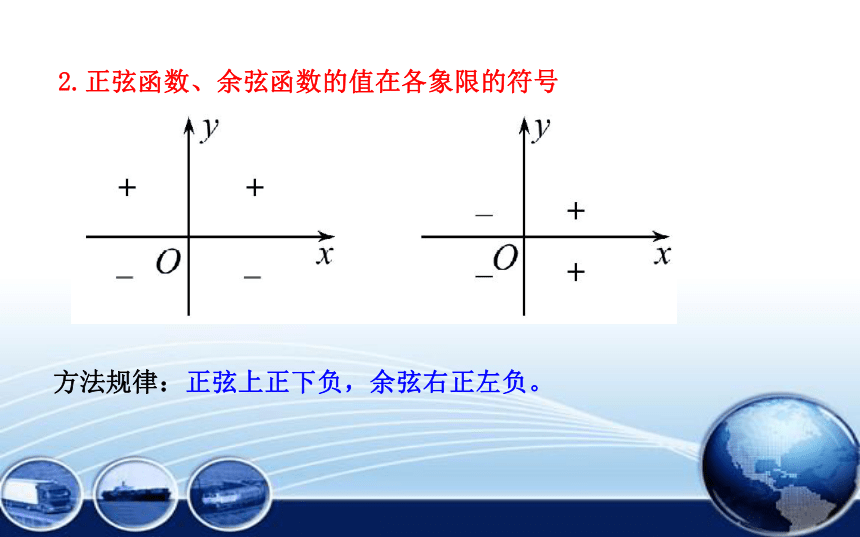
2.正弦函数、余弦函数的值在各象限的符号
方法规律:正弦上正下负,余弦右正左负。
3.任意角的正弦函数、余弦函数
(1)前提:设角α的顶点是坐标系的原点,始边与x轴的非负半
轴重合,角α终边上任一点Q(x,y).
(2)结论:OQ的长度为
且sin
α=___,cos
α=___.
1.判一判(正确的打“√”,错误的打“×”)
(1)sin
α,cos
α中可以将“α”与“sin”,“cos”分开.(
)
(2)同一个三角函数值能找到无数个角与之对应.(
)
(3)角α终边上有一点P(1,1),故cosα=1.(
)
【解析】(1)错误.符号sin
α,cos
α是一个整体,不能分开.
(2)正确.终边相同的角的同一三角函数值相等.
(3)错误.P(1,1),x=1,y=1,
故cos
α=
×
√
×
2.做一做(请把正确的答案写在横线上)
(1)已知角α终边经过点
则角α的最小正值是______.
(2)角α的终边经过点P(m,4),且cos
α=
则m=_______.
(3)角α满足sin
α>0,cos
α<0,则α在第______象限.
【解析】(1)
所以α的最小正值为
答案:
(2)r=
因为cosα=
解得m=3(舍去),m=-3.
答案:-3
(3)当sin
α>0时,α在第一、二象限及y轴正半轴,当
cos
α<0时,α在第二、三象限及x轴负半轴,故
sin
α>0,cos
α<0时,α在第二象限.
答案:二
【即时练】
当角α=0时,sin
α=______;若角α=-3,则sin
α的符号为______(填“正”或“负”).
【解析】当角α=0时,sin
α=0;若角α=-3,则角α是第三象限角,所以sin
α<0.
答案:0
负
【题型示范】
类型一
任意角的正弦函数、余弦函数
【典例1】
(1)(2014·石家庄高一检测)已知角α与单位圆的一个交点坐
标是
则cos
α等于(
)
(2)已知角α的终边经过点P(-2,-4),求角α的正、余弦函
数值.
【自主解答】(1)选D.因为
所以
故cos
α=
(2)因为点P(-2,-4)在角α的终边上,故u1=-2,
v1=-4,可知r=
OP
=
所以sin
α=
cos
α=
【变式训练】已知角α的终边经过点P(2,-3),则cos
α的值
是(
)
【解析】选C.角α的终边经过点P(2,-3),故
由三
角函数的定义知
故选C.
【考题链接】(2013·西安高一检测)已知角α为第二象限的角.
P(a,4)为α终边上一点,且sinα=
则sinα+cosα的值为____
.
【解析】|OP|=r=
由sinα=
得
所以a=±3.
又α为第二象限的角,
所以a=-3,所以cos
α=
所以sin
α+cos
α=
1
5
类型二
三角函数值的符号的应用
【典例2】
(1)(已知角α是第二象限角,则点P(sin
α,cos
α)在第__
象限.
(2)确定下列各式的符号.
①cos200°.
②sin160°+cos(-40°).
③sin210°·cos260°.
【自主解答】(1)因为角α是第二象限角,所以sin
α>0,cos
α<0,所以点P的坐标符号是(+,-),所以点P在第四象限.
(2)①200°为第三象限的角,所以cos
200°<0.
②160°为第二象限的角,所以sin
160°>0.-40°为第四象限的角,所以cos(-40°)>0,所以sin
160°+cos(-40°)>0.
③210°为第三象限的角,sin
210°<0,260°为第三象限的角,
所以cos
260°<0,所以sin
210°·cos
260°>0.
四
【方法技巧】正弦、余弦函数值的正负规律
【变式训练】确定下列各式的符号.
(1)sin
2
014°.
(2)
(3)sin
4·cos
4.
【解析】(1)2
014°=360°×5+214°,所以2
014°为第三象限的角,所以sin
2
014°<0.
(2)
为第四象限的角,所以cos
>0.
(3)4∈
所以4
rad为第三象限的角.
所以cos
4<0,sin
4<0.
所以sin
4·cos
4>0.
【考题链接】(2014·西安高一检测)
sin(-140°)cos
740°的值(
)
A.大于0
B.等于0
C.小于0
D.不确定
【解析】选C.
-140°是第三象限角,所以sin(-140°)<0,
740°=2×360°+20°,所以740°是第一象限角,所以
cos
740°>0,所以sin(-140°)cos
740°<0.
C
【易错误区】处理三角函数问题时忽视参数的符号致误
【典例】(2014·泰安高一检测)已知角α的终边经过点
P(-3m,m)(m≠0),则sin
α=_____或__.
错解
错
因
剖
析
忽略了对参数m的取值符号的讨论,而得到错误结果
【解析】由题意得:
|OP|=
当m>0时,|OP|=
则sinα=
当m<0时,|OP|=
则sinα=
答案:
或
【类题试解】已知角α的终边过点P(-3a,4a)(a≠0),则
cos
α=____或____.
【解析】由题意可得:|OP|=
当a>0时,|OP|=5a,则
当a<0时,|OP|=-5a,则
答案:
或
课
堂
总
结
1、任意角三角函数的定义:
2、解题方法总结
(1)已知交点P的坐标,直接用定义
(2)已知角,则先求交点P的坐标再用定义
若已知角α终边与单位圆交于点P(u,v),则:
3、正弦、余弦函数值的正负规律
正弦上正下负,余弦右正左负。
v
=
a
sin
u
=
a
cos
再
见!
感
谢
指
导
!
4.1
单位圆与任意角的正弦函数、
余弦函数的定义
问题
引航
1.单位圆中是如何定义正、余弦函数的?正、余弦函数的定义域是什么?
2.正、余弦函数在各个象限的符号如何确定?
3.任意角的三角函数的定义是什么?
锐角的正弦、余弦函数的定义:
对边
邻边
斜边
以原点为O圆心,以单位长度为半径的圆叫做单位圆.
x(1,0)
O
P(u,v)
α
y
M
x
当点P(u,v)
就是
的终边与单位圆的交点时,锐角三角函数会有什么结果?
下面我们在直角坐标系中,利用单位圆来进一步研究锐角
的正弦函数、余弦函数
任意角的正弦函数、余弦函数定义:
x
y
O
P(u,v)
α
A(1,0)
(1)v叫做α的正弦,记作sinα,
即sinα=v;
(2)u叫做α的余弦,记作
cosα,即cosα=u
如图,设α是一个任意角,它的终边与单位圆交于点P(u,v),那么:
三角函数
都是以角为自变量,以单位圆上的点的坐标(比值)为函数值的函数.
角(弧度数)
实数
三角函数可以看成是自变量为实数的函数
一一对应
定义域
函数
1.单位圆中任意角的正弦函数、余弦函数
v
u
全体实数
全体实数
2.正弦函数、余弦函数的值在各象限的符号
方法规律:正弦上正下负,余弦右正左负。
3.任意角的正弦函数、余弦函数
(1)前提:设角α的顶点是坐标系的原点,始边与x轴的非负半
轴重合,角α终边上任一点Q(x,y).
(2)结论:OQ的长度为
且sin
α=___,cos
α=___.
1.判一判(正确的打“√”,错误的打“×”)
(1)sin
α,cos
α中可以将“α”与“sin”,“cos”分开.(
)
(2)同一个三角函数值能找到无数个角与之对应.(
)
(3)角α终边上有一点P(1,1),故cosα=1.(
)
【解析】(1)错误.符号sin
α,cos
α是一个整体,不能分开.
(2)正确.终边相同的角的同一三角函数值相等.
(3)错误.P(1,1),x=1,y=1,
故cos
α=
×
√
×
2.做一做(请把正确的答案写在横线上)
(1)已知角α终边经过点
则角α的最小正值是______.
(2)角α的终边经过点P(m,4),且cos
α=
则m=_______.
(3)角α满足sin
α>0,cos
α<0,则α在第______象限.
【解析】(1)
所以α的最小正值为
答案:
(2)r=
因为cosα=
解得m=3(舍去),m=-3.
答案:-3
(3)当sin
α>0时,α在第一、二象限及y轴正半轴,当
cos
α<0时,α在第二、三象限及x轴负半轴,故
sin
α>0,cos
α<0时,α在第二象限.
答案:二
【即时练】
当角α=0时,sin
α=______;若角α=-3,则sin
α的符号为______(填“正”或“负”).
【解析】当角α=0时,sin
α=0;若角α=-3,则角α是第三象限角,所以sin
α<0.
答案:0
负
【题型示范】
类型一
任意角的正弦函数、余弦函数
【典例1】
(1)(2014·石家庄高一检测)已知角α与单位圆的一个交点坐
标是
则cos
α等于(
)
(2)已知角α的终边经过点P(-2,-4),求角α的正、余弦函
数值.
【自主解答】(1)选D.因为
所以
故cos
α=
(2)因为点P(-2,-4)在角α的终边上,故u1=-2,
v1=-4,可知r=
OP
=
所以sin
α=
cos
α=
【变式训练】已知角α的终边经过点P(2,-3),则cos
α的值
是(
)
【解析】选C.角α的终边经过点P(2,-3),故
由三
角函数的定义知
故选C.
【考题链接】(2013·西安高一检测)已知角α为第二象限的角.
P(a,4)为α终边上一点,且sinα=
则sinα+cosα的值为____
.
【解析】|OP|=r=
由sinα=
得
所以a=±3.
又α为第二象限的角,
所以a=-3,所以cos
α=
所以sin
α+cos
α=
1
5
类型二
三角函数值的符号的应用
【典例2】
(1)(已知角α是第二象限角,则点P(sin
α,cos
α)在第__
象限.
(2)确定下列各式的符号.
①cos200°.
②sin160°+cos(-40°).
③sin210°·cos260°.
【自主解答】(1)因为角α是第二象限角,所以sin
α>0,cos
α<0,所以点P的坐标符号是(+,-),所以点P在第四象限.
(2)①200°为第三象限的角,所以cos
200°<0.
②160°为第二象限的角,所以sin
160°>0.-40°为第四象限的角,所以cos(-40°)>0,所以sin
160°+cos(-40°)>0.
③210°为第三象限的角,sin
210°<0,260°为第三象限的角,
所以cos
260°<0,所以sin
210°·cos
260°>0.
四
【方法技巧】正弦、余弦函数值的正负规律
【变式训练】确定下列各式的符号.
(1)sin
2
014°.
(2)
(3)sin
4·cos
4.
【解析】(1)2
014°=360°×5+214°,所以2
014°为第三象限的角,所以sin
2
014°<0.
(2)
为第四象限的角,所以cos
>0.
(3)4∈
所以4
rad为第三象限的角.
所以cos
4<0,sin
4<0.
所以sin
4·cos
4>0.
【考题链接】(2014·西安高一检测)
sin(-140°)cos
740°的值(
)
A.大于0
B.等于0
C.小于0
D.不确定
【解析】选C.
-140°是第三象限角,所以sin(-140°)<0,
740°=2×360°+20°,所以740°是第一象限角,所以
cos
740°>0,所以sin(-140°)cos
740°<0.
C
【易错误区】处理三角函数问题时忽视参数的符号致误
【典例】(2014·泰安高一检测)已知角α的终边经过点
P(-3m,m)(m≠0),则sin
α=_____或__.
错解
错
因
剖
析
忽略了对参数m的取值符号的讨论,而得到错误结果
【解析】由题意得:
|OP|=
当m>0时,|OP|=
则sinα=
当m<0时,|OP|=
则sinα=
答案:
或
【类题试解】已知角α的终边过点P(-3a,4a)(a≠0),则
cos
α=____或____.
【解析】由题意可得:|OP|=
当a>0时,|OP|=5a,则
当a<0时,|OP|=-5a,则
答案:
或
课
堂
总
结
1、任意角三角函数的定义:
2、解题方法总结
(1)已知交点P的坐标,直接用定义
(2)已知角,则先求交点P的坐标再用定义
若已知角α终边与单位圆交于点P(u,v),则:
3、正弦、余弦函数值的正负规律
正弦上正下负,余弦右正左负。
v
=
a
sin
u
=
a
cos
再
见!
感
谢
指
导
!
