1.42 余弦三角函数的图像和性质课件(共有19张PPT)
文档属性
| 名称 | 1.42 余弦三角函数的图像和性质课件(共有19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 423.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-21 12:59:40 | ||
图片预览




文档简介
(共19张PPT)
1.4三角函数的图像及性质
5.6.2余弦函数的图像和性质
一、表达式:
1、形如:y
=
cosx
的函数叫余弦函数.其中x是自变量.
当x是角度制时可取一切角度,当x代表弧度制是可取一切实数,x∈R
二、余弦函数的图像及画法:
1、因为cos(α+2kπ)
=
cosα,
所以
y
=
cosx
是周期函数,
且周期是2π。
2、只需要作出【0,2π】上的图像,然后根据周期性,
扩展到一切实数R范围。
3、作函数图像的步骤:在函数定义域内:(代数作图法)书P128①
列表(算值)
②
描点(建立坐标系)③
连线
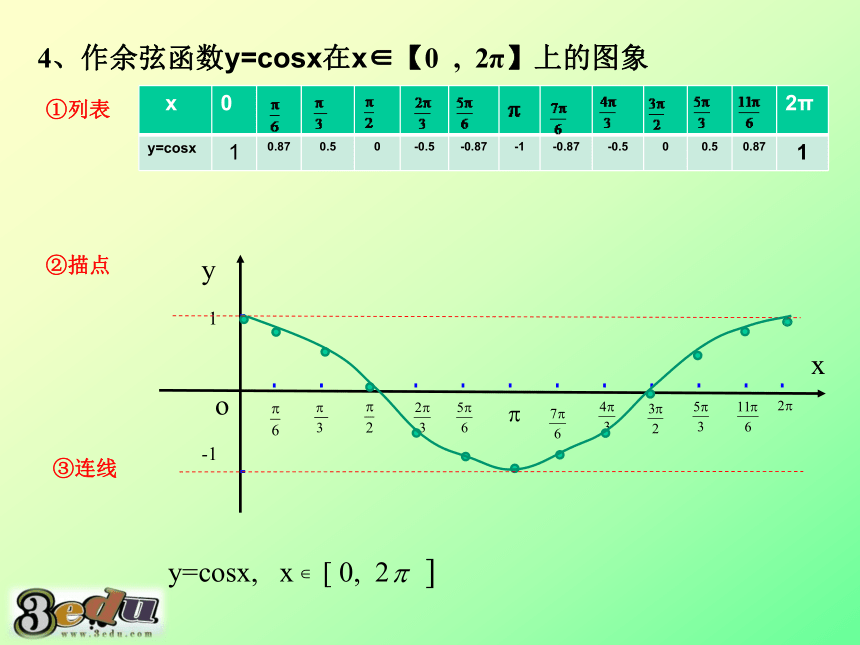
4、作余弦函数y=cosx在x∈【0
,
2π】上的图象
x
y
y=cosx,
x
[
0,
2
]
o
-1
1
①列表
x
0
2π
y=cosx
1
0.87
0.5
0
-0.5
-0.87
-1
-0.87
-0.5
0
0.5
0.87
1
②描点
③连线
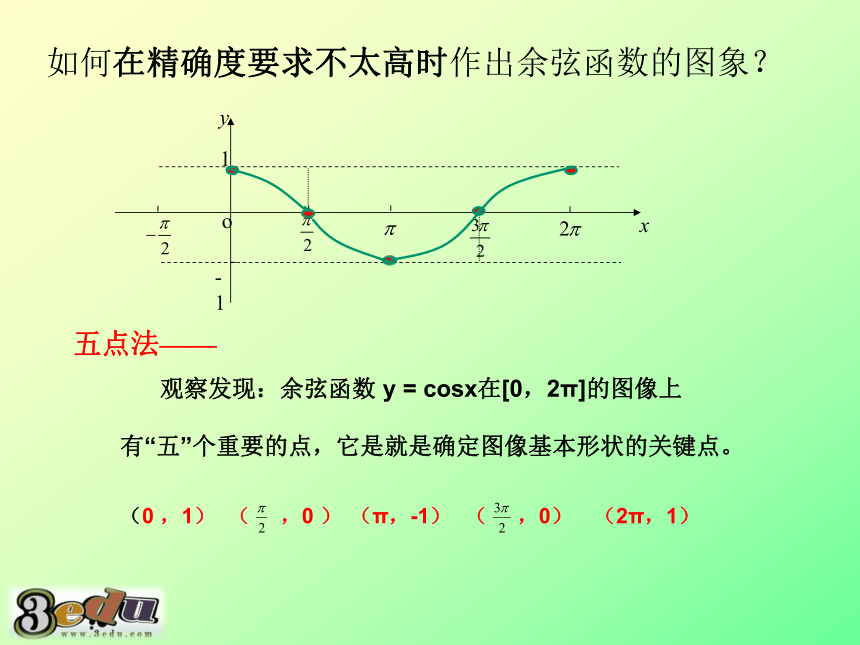
如何在精确度要求不太高时作出余弦函数的图象?
y
x
o
1
-1
五点法——
观察发现:余弦函数
y
=
cosx在[0,2π]的图像上
有“五”个重要的点,它是就是确定图像基本形状的关键点。
(0
,1)
(
,0
)
(π,-1)
(
,0)
(2π,1)
例:用“五点法”作函数图像:
1利用“五点法”作函数y
=
-cosx在【0,
2π】上的图像
O
X
y
.
解:①列表
x
0
π
2π
cosx
1
0
-1
0
1
y=-cosx
-1
0
1
0
-1
②描点
2π
.
1
-1
请观察:y
=
cosx与y
=
-cosx图像的区别与联系?
?连线
y
=
-
cosx
的图像
y
=
cosx
的图像
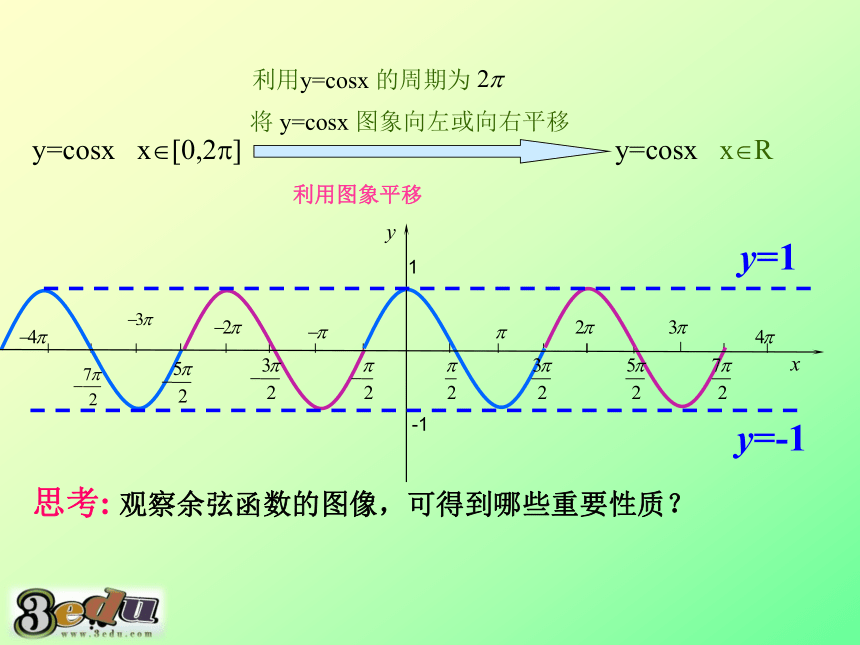
y=cosx
x?[0,2?]
y=cosx
x?R
利用y=cosx
的周期为
将
y=cosx
图象向左或向右平移
利用图象平移
x
y
1
-1
y=1
y=-1
思考:
观察余弦函数的图像,可得到哪些重要性质?
-
-
-
-
-
-
-
-
-
由
知余弦函数的图像可以通过正弦曲线向左平移
各单位长度而得到.
x
y
0
1
-1
想一想:
余弦函数又有什么样的性质呢?
四、余弦函数的性质
y=cosx
(x?R)
1、定义域:
X∈R(或一切角)
2、值
域:
y∈[-1
,
1](有界性)即
|cosx|
≤
1,或-1≤
y
≤1
其中:①当x=
(k∈z)时,y有最大值,ymax
=
1
②当x=
(k∈z)时,y有最小值,ymin
=
-1
3、周期性:
y
=
cosx
是周期为2π的周期函数
4、奇偶性:
是偶函数,y
=
cosx
的图像关于y轴对称.
或cos(-α)=
cosα,
y
x
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
例题:(
根据函数的性质解题)
1
、已知:2cosx=a-
4
,求a的取值范围。
解:根据正弦函数y
=
cosx的有界性:
所以
|a
-
4
|
≤
2
即
,-2
≤
a
-
4
≤
2
解得
2
≤
a
≤
6
故a的取值范围a∈[
2,
6
]
2、求使函数y
=
cos2x取得最大值的的集合,并指出最大值是多少?
解:根据正弦函数y
=
cosx的最大是1
,
设
u
=
2x
则y
=
cos2x
化为
y
=
cos
u
因为|cosx|≤1
即当u
=
时(k∈z),ymax=1
即
u
=
2x
=
解之x
=
(k∈z)
所以集合{x|x=
,
k∈z
}
函数y
=
cos2x取得最大值是1
,|2cosx|≤2
四、余弦函数的性质
y=cosx
(x?R)
5、单调性:
①在每一个区间【
】(k∈R)上都是增函数
②在每一个区间【
】(k∈R)上都是增减数
函数值y由
-1(最小)
增大到
1(最大)
函数值y由
1
(最大)减小到
-1(最小)
y
x
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
注意:
y
x
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
三、余弦弦函数的性质
1
定义域:
___________
2
值域:
当x=_______
时,y
取到最大值_______
当x=_______
时,y
取到最小值_______
3
奇偶性:
图像关于_______
对称,故为__________函数
4
周期:___________
5
单调性:单调增区间___________
单调减区间___________
6
对称轴:___________
x
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
练一练:
练一练:
y
x
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
例1
利用三角函数的单调性,比较下列各组数的大小
(1)
sin(
)
与sin(
)
∵
又
y=sinx
在
上是增函数
∵
sin(
)
<
sin(
)
(2)
cos(
)
与
cos(
)
解:
解:
从而
cos(
)=cos
=cos
cos(
)=cos
=cos
∵
又
y=cosx
在
上是减函数
∵
cos
即:
cos
–
cos
<0
cos(
)
<
cos(
)
例2
求下列函数的最大值和最小值,并写出取最大值、
最小值时自变量x的集合
(2)令u=2x,使函数y=-3sinz,z∈R
例3
求函数
的单调递增区间。
解:令
,函数
的单调递增区间是
由
得
设
所以
故此函数的单调递增区间是
例5
达标检测
1、比较大小
2、求使下列函数取得最大值的自变量的集合,并说出最大值是什么?
(1)
(2)
3、求函数
的定义域
4、
1.4三角函数的图像及性质
5.6.2余弦函数的图像和性质
一、表达式:
1、形如:y
=
cosx
的函数叫余弦函数.其中x是自变量.
当x是角度制时可取一切角度,当x代表弧度制是可取一切实数,x∈R
二、余弦函数的图像及画法:
1、因为cos(α+2kπ)
=
cosα,
所以
y
=
cosx
是周期函数,
且周期是2π。
2、只需要作出【0,2π】上的图像,然后根据周期性,
扩展到一切实数R范围。
3、作函数图像的步骤:在函数定义域内:(代数作图法)书P128①
列表(算值)
②
描点(建立坐标系)③
连线
4、作余弦函数y=cosx在x∈【0
,
2π】上的图象
x
y
y=cosx,
x
[
0,
2
]
o
-1
1
①列表
x
0
2π
y=cosx
1
0.87
0.5
0
-0.5
-0.87
-1
-0.87
-0.5
0
0.5
0.87
1
②描点
③连线
如何在精确度要求不太高时作出余弦函数的图象?
y
x
o
1
-1
五点法——
观察发现:余弦函数
y
=
cosx在[0,2π]的图像上
有“五”个重要的点,它是就是确定图像基本形状的关键点。
(0
,1)
(
,0
)
(π,-1)
(
,0)
(2π,1)
例:用“五点法”作函数图像:
1利用“五点法”作函数y
=
-cosx在【0,
2π】上的图像
O
X
y
.
解:①列表
x
0
π
2π
cosx
1
0
-1
0
1
y=-cosx
-1
0
1
0
-1
②描点
2π
.
1
-1
请观察:y
=
cosx与y
=
-cosx图像的区别与联系?
?连线
y
=
-
cosx
的图像
y
=
cosx
的图像
y=cosx
x?[0,2?]
y=cosx
x?R
利用y=cosx
的周期为
将
y=cosx
图象向左或向右平移
利用图象平移
x
y
1
-1
y=1
y=-1
思考:
观察余弦函数的图像,可得到哪些重要性质?
-
-
-
-
-
-
-
-
-
由
知余弦函数的图像可以通过正弦曲线向左平移
各单位长度而得到.
x
y
0
1
-1
想一想:
余弦函数又有什么样的性质呢?
四、余弦函数的性质
y=cosx
(x?R)
1、定义域:
X∈R(或一切角)
2、值
域:
y∈[-1
,
1](有界性)即
|cosx|
≤
1,或-1≤
y
≤1
其中:①当x=
(k∈z)时,y有最大值,ymax
=
1
②当x=
(k∈z)时,y有最小值,ymin
=
-1
3、周期性:
y
=
cosx
是周期为2π的周期函数
4、奇偶性:
是偶函数,y
=
cosx
的图像关于y轴对称.
或cos(-α)=
cosα,
y
x
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
例题:(
根据函数的性质解题)
1
、已知:2cosx=a-
4
,求a的取值范围。
解:根据正弦函数y
=
cosx的有界性:
所以
|a
-
4
|
≤
2
即
,-2
≤
a
-
4
≤
2
解得
2
≤
a
≤
6
故a的取值范围a∈[
2,
6
]
2、求使函数y
=
cos2x取得最大值的的集合,并指出最大值是多少?
解:根据正弦函数y
=
cosx的最大是1
,
设
u
=
2x
则y
=
cos2x
化为
y
=
cos
u
因为|cosx|≤1
即当u
=
时(k∈z),ymax=1
即
u
=
2x
=
解之x
=
(k∈z)
所以集合{x|x=
,
k∈z
}
函数y
=
cos2x取得最大值是1
,|2cosx|≤2
四、余弦函数的性质
y=cosx
(x?R)
5、单调性:
①在每一个区间【
】(k∈R)上都是增函数
②在每一个区间【
】(k∈R)上都是增减数
函数值y由
-1(最小)
增大到
1(最大)
函数值y由
1
(最大)减小到
-1(最小)
y
x
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
注意:
y
x
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
三、余弦弦函数的性质
1
定义域:
___________
2
值域:
当x=_______
时,y
取到最大值_______
当x=_______
时,y
取到最小值_______
3
奇偶性:
图像关于_______
对称,故为__________函数
4
周期:___________
5
单调性:单调增区间___________
单调减区间___________
6
对称轴:___________
x
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
练一练:
练一练:
y
x
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
例1
利用三角函数的单调性,比较下列各组数的大小
(1)
sin(
)
与sin(
)
∵
又
y=sinx
在
上是增函数
∵
sin(
)
<
sin(
)
(2)
cos(
)
与
cos(
)
解:
解:
从而
cos(
)=cos
=cos
cos(
)=cos
=cos
∵
又
y=cosx
在
上是减函数
∵
cos
cos
–
cos
<0
cos(
)
<
cos(
)
例2
求下列函数的最大值和最小值,并写出取最大值、
最小值时自变量x的集合
(2)令u=2x,使函数y=-3sinz,z∈R
例3
求函数
的单调递增区间。
解:令
,函数
的单调递增区间是
由
得
设
所以
故此函数的单调递增区间是
例5
达标检测
1、比较大小
2、求使下列函数取得最大值的自变量的集合,并说出最大值是什么?
(1)
(2)
3、求函数
的定义域
4、
