苏科版数学八年级下册 第9章中心对称图形 平行四边形 小结与思考 教案
文档属性
| 名称 | 苏科版数学八年级下册 第9章中心对称图形 平行四边形 小结与思考 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 100.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-20 00:00:00 | ||
图片预览

文档简介
第九章中心对称 小结与思考
教学目标:
1、回顾、总结本章所学相关概念、定理和思想方法
2、能对知识进行梳理,使所学知识系统化
3、会运用所学定理进行有关计算和证明。
教学重点:会运用所学定理进行有关计算和证明。
教学难点:熟练运用所学定理进行有关计算和证明。
教学方法与手段:多媒体教学 分组教学 教学案?导学
教学过程:
一、知识梳理:
1、图形的旋转、中心对称、中心对称图形及它们的区别与联系;
中心对称图形定义:
如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心;互相重合的点叫做对称点.
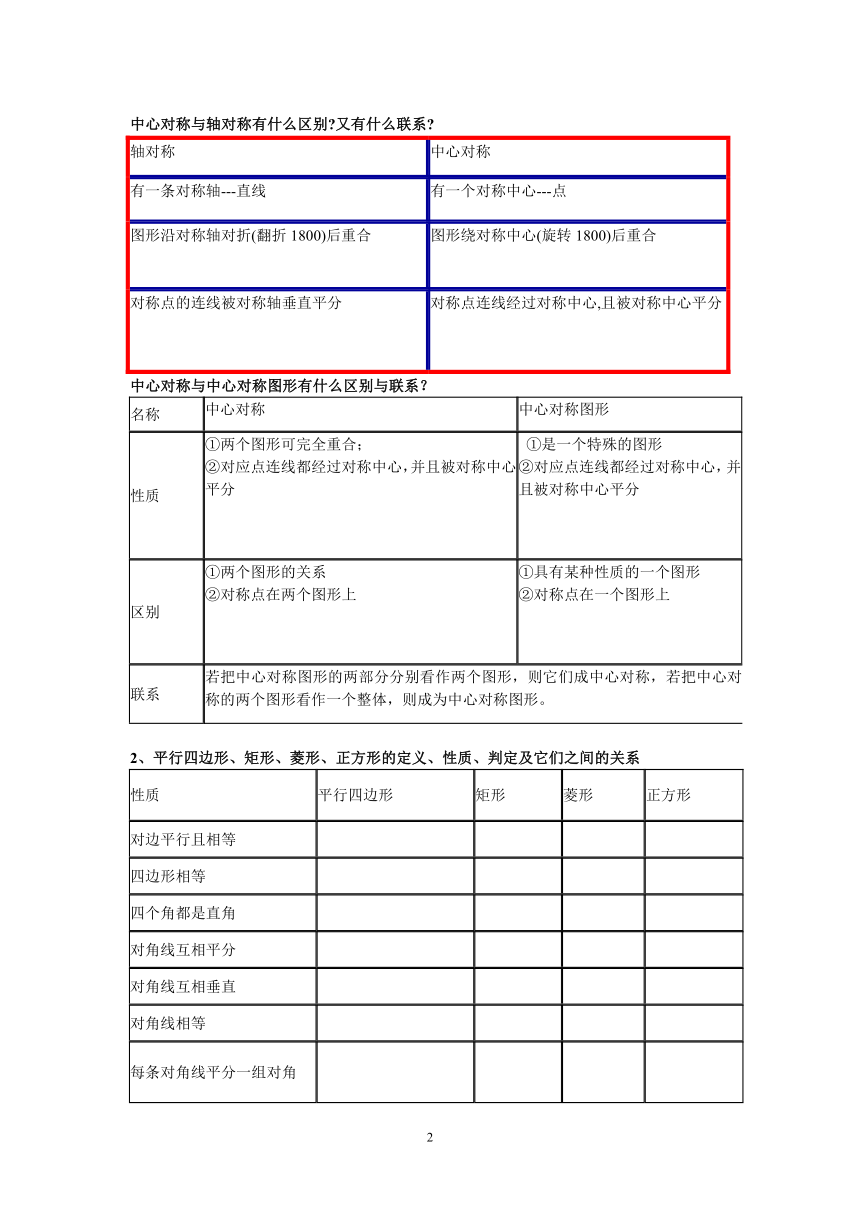
中心对称与轴对称有什么区别?又有什么联系?
轴对称 中心对称
有一条对称轴---直线 有一个对称中心---点
图形沿对称轴对折(翻折1800)后重合 图形绕对称中心(旋转1800)后重合
对称点的连线被对称轴垂直平分 对称点连线经过对称中心,且被对称中心平分
中心对称与中心对称图形有什么区别与联系?
名称 中心对称 中心对称图形
性质 ①两个图形可完全重合;
②对应点连线都经过对称中心,并且被对称中心平分 ①是一个特殊的图形
②对应点连线都经过对称中心,并且被对称中心平分
区别 ①两个图形的关系
②对称点在两个图形上 ①具有某种性质的一个图形
②对称点在一个图形上
联系 若把中心对称图形的两部分分别看作两个图形,则它们成中心对称,若把中心对称的两个图形看作一个整体,则成为中心对称图形。
2、平行四边形、矩形、菱形、正方形的定义、性质、判定及它们之间的关系
性质 平行四边形 矩形 菱形 正方形
对边平行且相等 ? ? ? ?
四边形相等 ? ? ? ?
四个角都是直角 ? ? ? ?
对角线互相平分 ? ? ? ?
对角线互相垂直 ? ? ? ?
对角线相等 ? ? ? ?
每条对角线平分一组对角 ? ? ? ?
3、三角形中位线
(1)三角形中位线的定义:
连接三角形两边中点的线段叫做三角形中位线
(2)三角形中位线性质:
三角形中位线平行于第三边,并且等于第三边的一半
直线l1∥l2,A、C是直线l1上的任意两点,AB⊥l2 ,CD⊥l2,垂足分别为B、D.线段AB、CD相等吗?为什么?
思考:
例1:已知:如图,D是△ABC的边
AB上一点,CN∥AB,DN交AC于点M,MA=MC.
①求证:CD=AN;
②若∠AMD=2∠MCD,求证:四边形ADCN是矩形
例2、如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.
求证:四边形BCDE是矩形.
例3、已知:如图,四边形ABCD中,AB=CD,BC=DA,对角线AC、BD交于点O.E是四边形ABCD外一点,AE⊥EC,BE⊥DE,试问:四边形ABCD是矩形, 并证明你的结论。
拓展延伸
1、如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN为△ABC的外角∠CAM的平分线,CE⊥AN,垂足为E,连接DE交AC于F,求证:DF∥AB,DF= AB。
课堂小结
板书设计:
教学反思:
2
教学目标:
1、回顾、总结本章所学相关概念、定理和思想方法
2、能对知识进行梳理,使所学知识系统化
3、会运用所学定理进行有关计算和证明。
教学重点:会运用所学定理进行有关计算和证明。
教学难点:熟练运用所学定理进行有关计算和证明。
教学方法与手段:多媒体教学 分组教学 教学案?导学
教学过程:
一、知识梳理:
1、图形的旋转、中心对称、中心对称图形及它们的区别与联系;
中心对称图形定义:
如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心;互相重合的点叫做对称点.
中心对称与轴对称有什么区别?又有什么联系?
轴对称 中心对称
有一条对称轴---直线 有一个对称中心---点
图形沿对称轴对折(翻折1800)后重合 图形绕对称中心(旋转1800)后重合
对称点的连线被对称轴垂直平分 对称点连线经过对称中心,且被对称中心平分
中心对称与中心对称图形有什么区别与联系?
名称 中心对称 中心对称图形
性质 ①两个图形可完全重合;
②对应点连线都经过对称中心,并且被对称中心平分 ①是一个特殊的图形
②对应点连线都经过对称中心,并且被对称中心平分
区别 ①两个图形的关系
②对称点在两个图形上 ①具有某种性质的一个图形
②对称点在一个图形上
联系 若把中心对称图形的两部分分别看作两个图形,则它们成中心对称,若把中心对称的两个图形看作一个整体,则成为中心对称图形。
2、平行四边形、矩形、菱形、正方形的定义、性质、判定及它们之间的关系
性质 平行四边形 矩形 菱形 正方形
对边平行且相等 ? ? ? ?
四边形相等 ? ? ? ?
四个角都是直角 ? ? ? ?
对角线互相平分 ? ? ? ?
对角线互相垂直 ? ? ? ?
对角线相等 ? ? ? ?
每条对角线平分一组对角 ? ? ? ?
3、三角形中位线
(1)三角形中位线的定义:
连接三角形两边中点的线段叫做三角形中位线
(2)三角形中位线性质:
三角形中位线平行于第三边,并且等于第三边的一半
直线l1∥l2,A、C是直线l1上的任意两点,AB⊥l2 ,CD⊥l2,垂足分别为B、D.线段AB、CD相等吗?为什么?
思考:
例1:已知:如图,D是△ABC的边
AB上一点,CN∥AB,DN交AC于点M,MA=MC.
①求证:CD=AN;
②若∠AMD=2∠MCD,求证:四边形ADCN是矩形
例2、如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.
求证:四边形BCDE是矩形.
例3、已知:如图,四边形ABCD中,AB=CD,BC=DA,对角线AC、BD交于点O.E是四边形ABCD外一点,AE⊥EC,BE⊥DE,试问:四边形ABCD是矩形, 并证明你的结论。
拓展延伸
1、如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN为△ABC的外角∠CAM的平分线,CE⊥AN,垂足为E,连接DE交AC于F,求证:DF∥AB,DF= AB。
课堂小结
板书设计:
教学反思:
2
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
