苏科版数学八年级下册 第11章 反比例函数 小结与思考 教案
文档属性
| 名称 | 苏科版数学八年级下册 第11章 反比例函数 小结与思考 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 276.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-20 00:00:00 | ||
图片预览

文档简介
八下期末复习
第十一章 反比例函数复习
复习目标:
1.进一步理解反比例函数的定义,会确定反比例函数的解析式;
2.灵活掌握反比例函数的图象及性质;
3.运用反比例函数解决某些问题。
复习过程:
一、基础知识回顾:
1.下面函数中,哪些是反比例函数?
(1) (2) (3) (4) (5)
2.若双曲线经过点(-3 ,2),则其解析式是______.
回忆:(1)形如 函数叫反比例函数;其中,叫 ,自变量的取值范围是 .
(2)反比例函数的解析式除了像定义中可以表示成,还可以将其变形表示成______
和 .
3.函数 的图象在第______象限,当x<0时, y随x的增大而______ .
4.函数 的图象在二、四象限内,m的取值范围是______ .在每个象限内,y随x的增大而____
回忆:填写下表:
k>0 k<0
图
像
位 置 函数图像的两个分支分别在第 象限 函数图像的两个分支分别在第 象限
增减性 在每个象限内,y随x的增大而 . 在每个象限内,y随x的增大而 .
渐近性 当x值的绝对值无限增大或接近于零时,它的两个分支都无限 x轴或y
轴,但永远不会与x轴y轴 。
5.如右图,直线y=2x与双曲线的图象的一个交点坐标为(2,4),
则它们的另一个交点坐标是( )
A(-2,-4) B(-2,4) C(-4,-2) D(2,-4)
回忆:反比例函数的图象既是_______又是_________。有______对称轴,对称中心是:____
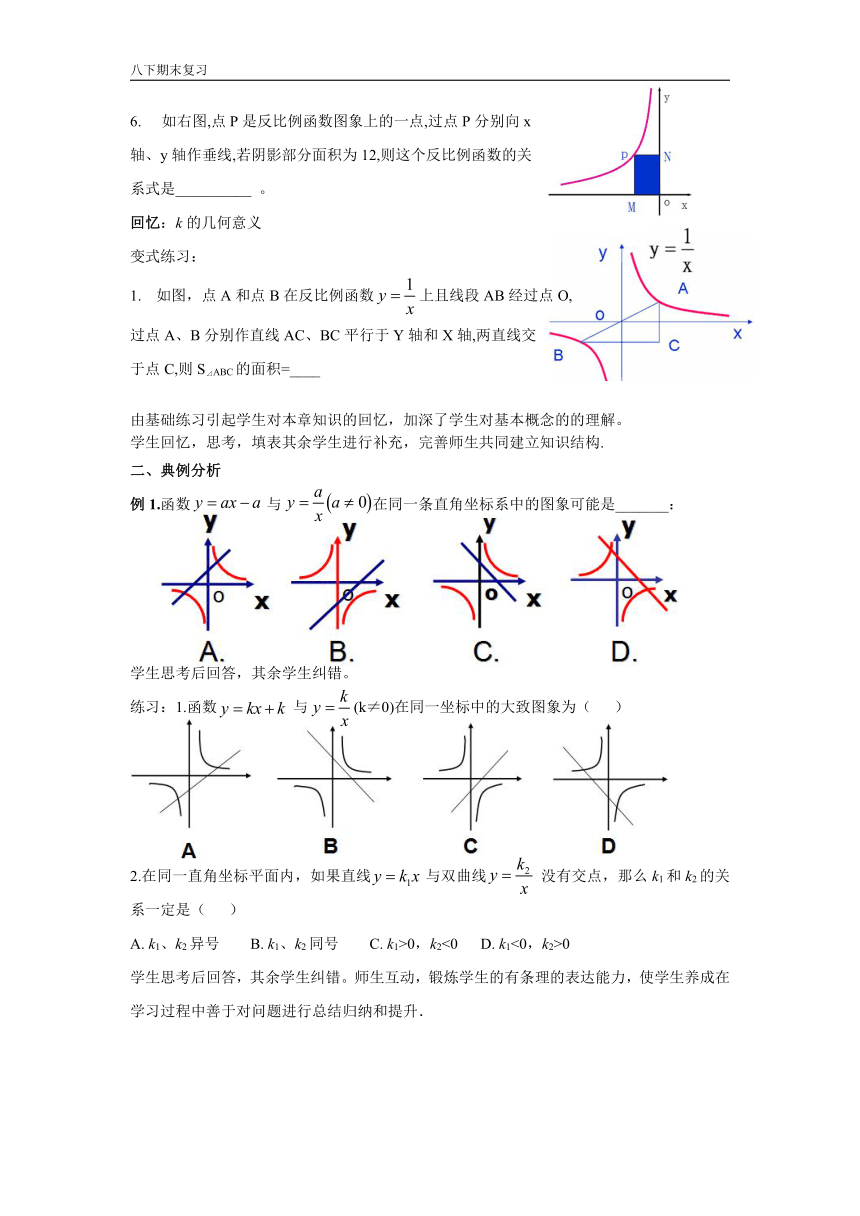
6. 如右图,点P是反比例函数图象上的一点,过点P分别向x
轴、y轴作垂线,若阴影部分面积为12,则这个反比例函数的关
系式是__________ 。
回忆:k的几何意义
变式练习:
如图,点A和点B在反比例函数上且线段AB经过点O,
过点A、B分别作直线AC、BC平行于Y轴和X轴,两直线交
于点C,则S⊿ABC的面积=____
由基础练习引起学生对本章知识的回忆,加深了学生对基本概念的的理解。
学生回忆,思考,填表其余学生进行补充,完善师生共同建立知识结构.
二、典例分析
例1.函数 与 在同一条直角坐标系中的图象可能是_______:
学生思考后回答,其余学生纠错。
练习:1.函数 与 (k≠0)在同一坐标中的大致图象为( )
2.在同一直角坐标平面内,如果直线 与双曲线 没有交点,那么k1和k2的关系一定是( )
A. k1、k2异号 B. k1、k2同号 C. k1>0,k2<0 D. k1<0,k2>0
学生思考后回答,其余学生纠错。师生互动,锻炼学生的有条理的表达能力,使学生养成在学习过程中善于对问题进行总结归纳和提升.
3.所受压力为F (F为常数且F≠ 0) 的物体,所受压强P与所受面积S的图象大致为( )
A B C D
引导学生根据实际问题的条件确定函数的类型,并确定反比例函数自变量的取值范围并画出正确的图像.体会该图像是双曲线的一支.
例2 已知点A(-2,y1),B(-1,y2)都在反比例函数 的图象上,则y1与y2的大小关系(从大到小)为 .
学生尝试解题, 学生思考后回答,其余学生纠错。
学生评判。并问学生用什么方法解决的,讨论多种解法。图象法或增减性。
练习:1. 已知点A(x1,y1),B(x2,y2)且x1<0<x2都在反比例函数 的图象上,则y1与y2的大小关系(从大到小)为 .
2.已知P1(x1,y1),P2(x2,y2),P3(x3,y3)是反比例函数 的图象上三点,且y1<y2<0<y3,则x1,x2,x3的大小关系是( )
A. x1通过学生相互讨论使学生主动参与到学习活动中来,培养学生小组合作意识.练习1让学生口答,练习2让学生展示。通过学生相互讨论,培养学生对问题的分析以及归纳能力,提高学生的数学语言表达能力.
例3.如图,一次函数y=kx+b的图象与反比例函数 的图象交A(-2,1),B(1,n)于两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)根据图象写出使一次函数的值小于反比例函数的值
的x的取值范围.
(3)求△AOB的面积.
数形结合进行解题。
学生尝试解题,师生共同探索解题方法。
(1)把A点的坐标代入,通过两点确定解析式。(2)根据A B两点坐标,通过观察图象写出范围。
(3)转化成易求两个的三角形的面积来求解,鼓励学生用多种方法来解题.
练习:如图,一次函数y=kx+b与反比例函数 的图象交于A(1,6),B(3,n)两点
根据图象写出不等式 的解集是 .
三、小结:
1.反比例函数解析式常见的几种形式
2.反比例函数图像的形状,位置,增减性,对称性,面积不变性。
3.一些基本题型的解题要点
4.反比例函数在生活中的应用
5.做题时要注意数形结合
四.当堂反馈:
1. 已知,是反比例函数,则m= ,此函数图象在第 象限。
2. 一批零件300个,一个工人每小时做15个,用关系式表示人数与完成任务所需的时间之间的函数关系式为________ .
3.函数与(a≠0)在同一直角坐标系中的图象可能是( )
4.一张正方形的纸片,剪去两个一样的小矩形得到一个“”图案,如图所示,设小矩形的长和宽分别为、,剪去部分的面积为20,若,则与的函数图象是( )
5. 下列函数中,当x>0时,y随x的增大而增大的是 ( )
A. y=2-3x B. y= C .y=-2x-1 D. y=-
6.有一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度(单位:kg/m3)是体积V(单位:m3)的反比例函数,它的图象如图所示,当V=2m3时,气体的密度是_______kg/m3.
第6题 第7题
7.如图,已知梯形ABCO的底边AO在轴上,BC∥AO,AB⊥AO,过点C的双曲线 交OB于D,且OD:DB=1:2,若△OBC的面积等于3,则k的值是
第十一章 反比例函数复习
复习目标:
1.进一步理解反比例函数的定义,会确定反比例函数的解析式;
2.灵活掌握反比例函数的图象及性质;
3.运用反比例函数解决某些问题。
复习过程:
一、基础知识回顾:
1.下面函数中,哪些是反比例函数?
(1) (2) (3) (4) (5)
2.若双曲线经过点(-3 ,2),则其解析式是______.
回忆:(1)形如 函数叫反比例函数;其中,叫 ,自变量的取值范围是 .
(2)反比例函数的解析式除了像定义中可以表示成,还可以将其变形表示成______
和 .
3.函数 的图象在第______象限,当x<0时, y随x的增大而______ .
4.函数 的图象在二、四象限内,m的取值范围是______ .在每个象限内,y随x的增大而____
回忆:填写下表:
k>0 k<0
图
像
位 置 函数图像的两个分支分别在第 象限 函数图像的两个分支分别在第 象限
增减性 在每个象限内,y随x的增大而 . 在每个象限内,y随x的增大而 .
渐近性 当x值的绝对值无限增大或接近于零时,它的两个分支都无限 x轴或y
轴,但永远不会与x轴y轴 。
5.如右图,直线y=2x与双曲线的图象的一个交点坐标为(2,4),
则它们的另一个交点坐标是( )
A(-2,-4) B(-2,4) C(-4,-2) D(2,-4)
回忆:反比例函数的图象既是_______又是_________。有______对称轴,对称中心是:____
6. 如右图,点P是反比例函数图象上的一点,过点P分别向x
轴、y轴作垂线,若阴影部分面积为12,则这个反比例函数的关
系式是__________ 。
回忆:k的几何意义
变式练习:
如图,点A和点B在反比例函数上且线段AB经过点O,
过点A、B分别作直线AC、BC平行于Y轴和X轴,两直线交
于点C,则S⊿ABC的面积=____
由基础练习引起学生对本章知识的回忆,加深了学生对基本概念的的理解。
学生回忆,思考,填表其余学生进行补充,完善师生共同建立知识结构.
二、典例分析
例1.函数 与 在同一条直角坐标系中的图象可能是_______:
学生思考后回答,其余学生纠错。
练习:1.函数 与 (k≠0)在同一坐标中的大致图象为( )
2.在同一直角坐标平面内,如果直线 与双曲线 没有交点,那么k1和k2的关系一定是( )
A. k1、k2异号 B. k1、k2同号 C. k1>0,k2<0 D. k1<0,k2>0
学生思考后回答,其余学生纠错。师生互动,锻炼学生的有条理的表达能力,使学生养成在学习过程中善于对问题进行总结归纳和提升.
3.所受压力为F (F为常数且F≠ 0) 的物体,所受压强P与所受面积S的图象大致为( )
A B C D
引导学生根据实际问题的条件确定函数的类型,并确定反比例函数自变量的取值范围并画出正确的图像.体会该图像是双曲线的一支.
例2 已知点A(-2,y1),B(-1,y2)都在反比例函数 的图象上,则y1与y2的大小关系(从大到小)为 .
学生尝试解题, 学生思考后回答,其余学生纠错。
学生评判。并问学生用什么方法解决的,讨论多种解法。图象法或增减性。
练习:1. 已知点A(x1,y1),B(x2,y2)且x1<0<x2都在反比例函数 的图象上,则y1与y2的大小关系(从大到小)为 .
2.已知P1(x1,y1),P2(x2,y2),P3(x3,y3)是反比例函数 的图象上三点,且y1<y2<0<y3,则x1,x2,x3的大小关系是( )
A. x1
例3.如图,一次函数y=kx+b的图象与反比例函数 的图象交A(-2,1),B(1,n)于两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)根据图象写出使一次函数的值小于反比例函数的值
的x的取值范围.
(3)求△AOB的面积.
数形结合进行解题。
学生尝试解题,师生共同探索解题方法。
(1)把A点的坐标代入,通过两点确定解析式。(2)根据A B两点坐标,通过观察图象写出范围。
(3)转化成易求两个的三角形的面积来求解,鼓励学生用多种方法来解题.
练习:如图,一次函数y=kx+b与反比例函数 的图象交于A(1,6),B(3,n)两点
根据图象写出不等式 的解集是 .
三、小结:
1.反比例函数解析式常见的几种形式
2.反比例函数图像的形状,位置,增减性,对称性,面积不变性。
3.一些基本题型的解题要点
4.反比例函数在生活中的应用
5.做题时要注意数形结合
四.当堂反馈:
1. 已知,是反比例函数,则m= ,此函数图象在第 象限。
2. 一批零件300个,一个工人每小时做15个,用关系式表示人数与完成任务所需的时间之间的函数关系式为________ .
3.函数与(a≠0)在同一直角坐标系中的图象可能是( )
4.一张正方形的纸片,剪去两个一样的小矩形得到一个“”图案,如图所示,设小矩形的长和宽分别为、,剪去部分的面积为20,若,则与的函数图象是( )
5. 下列函数中,当x>0时,y随x的增大而增大的是 ( )
A. y=2-3x B. y= C .y=-2x-1 D. y=-
6.有一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度(单位:kg/m3)是体积V(单位:m3)的反比例函数,它的图象如图所示,当V=2m3时,气体的密度是_______kg/m3.
第6题 第7题
7.如图,已知梯形ABCO的底边AO在轴上,BC∥AO,AB⊥AO,过点C的双曲线 交OB于D,且OD:DB=1:2,若△OBC的面积等于3,则k的值是
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
