苏科版数学八年级下册第12章 二次根式数学活动 画画 算算 教案
文档属性
| 名称 | 苏科版数学八年级下册第12章 二次根式数学活动 画画 算算 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 93.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-20 15:53:44 | ||
图片预览


文档简介
画画 算算
一.活动目标
(1)通过画图、列表、分析数据、寻找规律,发现并验证皮克定理;
(2)让学生在“做”中学,通过实际操作获得亲身体验,积累直接经验。强化学生在数学学习过程中的主体地位,发挥学生的积极性、主动性和创造性,自主地投入活动;
(3)通过动手操作、观察类比、分析归纳、合作交流等一系列探究活动,了解解决问题的过程和方法;经历从特殊到一般的过程,体验“在解决多变量问题中采用变量控制法”的科学思维方法。
二.活动重点
经历实践活动的过程,学会寻找思考问题的着眼点,掌握研究问题的方法,领悟数学思想。
活动难点
格点多边形的面积与图形内部及它边上的格点数之间关系的探究。
活动过程
网格纸上画着纵、横两组平行线,相邻的平行线之间的距离都相等,这样两组平行线的交点称为格点。
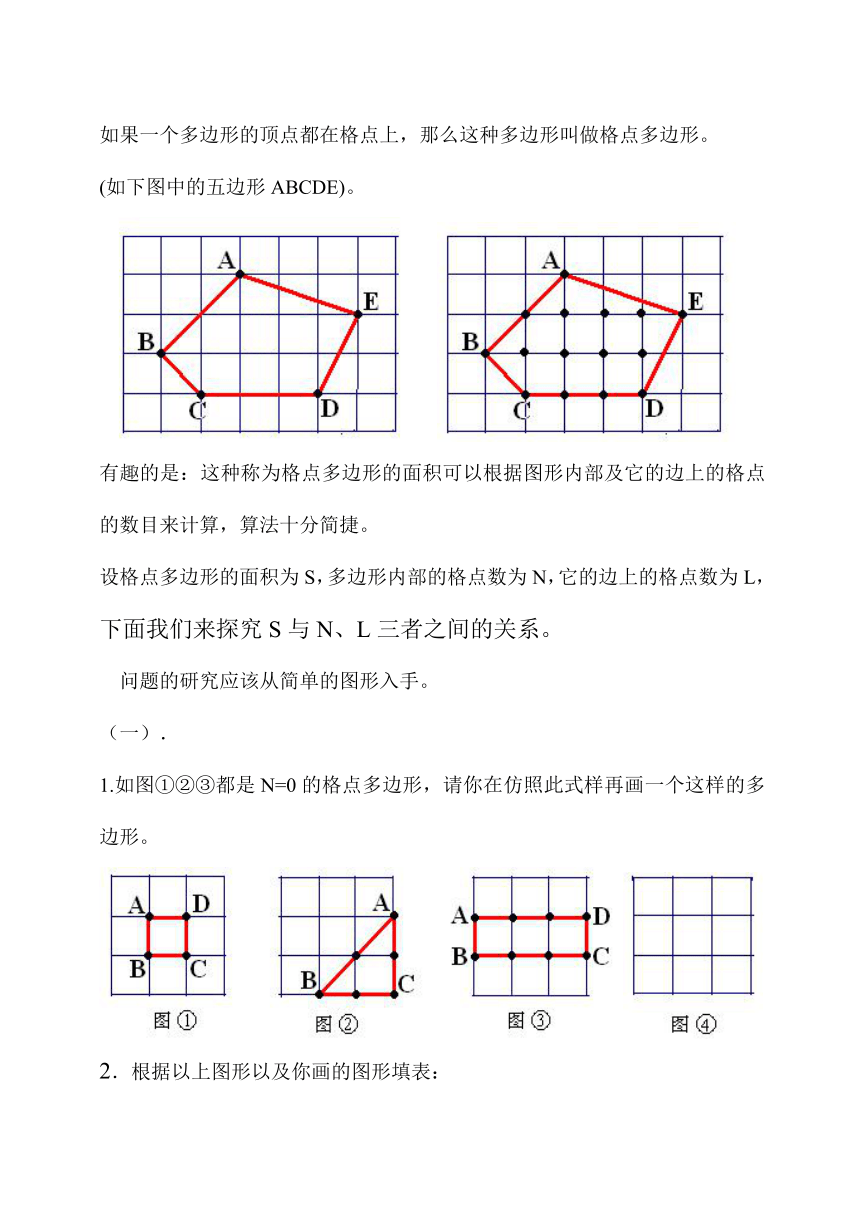
如果一个多边形的顶点都在格点上,那么这种多边形叫做格点多边形。
(如下图中的五边形ABCDE)。
有趣的是:这种称为格点多边形的面积可以根据图形内部及它的边上的格点的数目来计算,算法十分简捷。
设格点多边形的面积为S,多边形内部的格点数为N,它的边上的格点数为L, 下面我们来探究S与N、L三者之间的关系。
问题的研究应该从简单的图形入手。
.
1.如图①②③都是N=0的格点多边形,请你在仿照此式样再画一个这样的多边形。
2.根据以上图形以及你画的图形填表:
图形序号 S N L
① 1 0 4
② 2 0 6
③ 3 0 8
④
3.观察图表可以发现:。判断一下在你画的图中这个关系式是否成立?
(二).
1.如图⑤⑥⑦都是N= 1的格点多边形,请你在仿照此式样再画一个这样的多边形。
2.根据以上图形以及你画的图形填表:
图形序号 S N L
⑤ 2 1 4
⑥ 2.5 1 5
⑦ 4.5 1 9
⑧
3.观察上表,你有什么发现?怎样用N、L的代数式来表示S ?
(三).
1.如图⑨⑩都是N= 2的格点多边形,请你在仿照此式样再画一个这样的多边形。
2.根据以上图形以及你画的图形填表:
图形序号 S N L
⑨ 6 2 10
⑩ 4 2 6
3 2 4
观察上表,你有什么发现?怎样用N、L的代数式来表示 S?
(四).
1.如图、、都是N= 3的格点多边形,请你在仿照此式样再画一个这样的多边形。
2.根据以上图形以及你画的图形填表:
图形序号 S N L
5 3 6
4 3 4
4.5 3 5
3.观察上表,你有什么发现?怎样用N、L的代数式来表示 S?
(五).
综合分析与归纳:格点多边形的面积S与多边形内部的格点数N、它的边上的格点数L之间的数量关系式是。
这个公式是由奥地利数学家皮克(Georg Pick)在1899年给出的,所以这个公式被人称为皮克定理。这是一个实用而且有趣的定理。不过通常我们需要计算的图形 往往并不都是格点多边形。因此,在实际应用时,仍需要用割补的方法,将问题转化为面积相等的格点多边形,然后再用皮克定理进行计算。
一.活动目标
(1)通过画图、列表、分析数据、寻找规律,发现并验证皮克定理;
(2)让学生在“做”中学,通过实际操作获得亲身体验,积累直接经验。强化学生在数学学习过程中的主体地位,发挥学生的积极性、主动性和创造性,自主地投入活动;
(3)通过动手操作、观察类比、分析归纳、合作交流等一系列探究活动,了解解决问题的过程和方法;经历从特殊到一般的过程,体验“在解决多变量问题中采用变量控制法”的科学思维方法。
二.活动重点
经历实践活动的过程,学会寻找思考问题的着眼点,掌握研究问题的方法,领悟数学思想。
活动难点
格点多边形的面积与图形内部及它边上的格点数之间关系的探究。
活动过程
网格纸上画着纵、横两组平行线,相邻的平行线之间的距离都相等,这样两组平行线的交点称为格点。
如果一个多边形的顶点都在格点上,那么这种多边形叫做格点多边形。
(如下图中的五边形ABCDE)。
有趣的是:这种称为格点多边形的面积可以根据图形内部及它的边上的格点的数目来计算,算法十分简捷。
设格点多边形的面积为S,多边形内部的格点数为N,它的边上的格点数为L, 下面我们来探究S与N、L三者之间的关系。
问题的研究应该从简单的图形入手。
.
1.如图①②③都是N=0的格点多边形,请你在仿照此式样再画一个这样的多边形。
2.根据以上图形以及你画的图形填表:
图形序号 S N L
① 1 0 4
② 2 0 6
③ 3 0 8
④
3.观察图表可以发现:。判断一下在你画的图中这个关系式是否成立?
(二).
1.如图⑤⑥⑦都是N= 1的格点多边形,请你在仿照此式样再画一个这样的多边形。
2.根据以上图形以及你画的图形填表:
图形序号 S N L
⑤ 2 1 4
⑥ 2.5 1 5
⑦ 4.5 1 9
⑧
3.观察上表,你有什么发现?怎样用N、L的代数式来表示S ?
(三).
1.如图⑨⑩都是N= 2的格点多边形,请你在仿照此式样再画一个这样的多边形。
2.根据以上图形以及你画的图形填表:
图形序号 S N L
⑨ 6 2 10
⑩ 4 2 6
3 2 4
观察上表,你有什么发现?怎样用N、L的代数式来表示 S?
(四).
1.如图、、都是N= 3的格点多边形,请你在仿照此式样再画一个这样的多边形。
2.根据以上图形以及你画的图形填表:
图形序号 S N L
5 3 6
4 3 4
4.5 3 5
3.观察上表,你有什么发现?怎样用N、L的代数式来表示 S?
(五).
综合分析与归纳:格点多边形的面积S与多边形内部的格点数N、它的边上的格点数L之间的数量关系式是。
这个公式是由奥地利数学家皮克(Georg Pick)在1899年给出的,所以这个公式被人称为皮克定理。这是一个实用而且有趣的定理。不过通常我们需要计算的图形 往往并不都是格点多边形。因此,在实际应用时,仍需要用割补的方法,将问题转化为面积相等的格点多边形,然后再用皮克定理进行计算。
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
