2.2等差数列课件(苏教版必修5)
图片预览





文档简介
(共12张PPT)
观察下列数列:
(1) 6,3,0,-3,-6,-9,…
(2) 1,11,21,31,41,…
(3) 1,1,1,1,…
请同学们仔细观察,看看以上三个数列有什么共同的特征?
共同特征:从第二项起,每一项与它前面一项的差等于同一个常数。
我们给具有这种特征的数列一个名字------等差数列
定义:如果一个数列从第 ___ 项起,每一项与它的 ___ __的差等于 _____ 一常数 d,这个数列叫做 __________ ,d 为此数列的 __________。
二
前一项
同
等差数列
公差
问题1:由数列的前几项(有限项)按定义作差都为同一常数,能否说明此数列为等差数列?
不能
问题2:公差d一定是由 项减 项所得。
后
前
问题3:判断数列为等差数列的方法:
a n -a n -1 = d ( n ≥ 2 )
或 a n + 1 -a n = d ( n ≥ 1 )
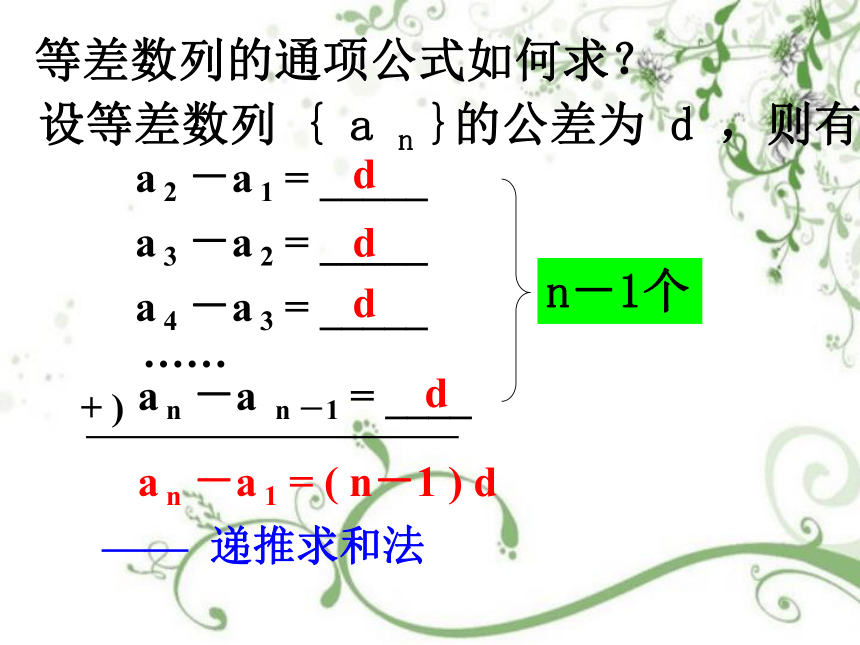
等差数列的通项公式如何求?
设等差数列 { a n }的公差为 d ,则有
a n -a n -1 = ____
a 2 -a 1 = _____
a 3 -a 2 = _____
a 4 -a 3 = _____
……
+ )
d
d
d
d
n-1个
a n -a 1 = ( n-1 ) d
—— 递推求和法
设等差数列 { a n }的公差为 d ,则有
a 2 = a 1 + ____
d
a 3 = a 2 + __ = a 1 + ___
d
2d
a 4 = a 3 + __ = a 1 + ___
d
3d
……
a n = a n -1 + _____ = a 1 + ______
d
(n-1)d
即:a n = a 1 + (n-1)d
—— 猜想论证法
等差数列的通项公式:
若等差数列 { a n } 的首项为 a 1,公差为 d ,则通项公式为
a n = a 1 + ( n-1 ) d,n ∈N +
等差数列中,a n 是 n 的 ____________,
图象特点 _________________________
一次函数
直线上的一些有规律的点
或 a n 是常数函数,公差为 d = _______
0
例1.(1)求等差数列8 , 5 , 2 ,…的第20项.
(2) - 401是不是等差数列- 5, - 9, - 13, …的项 如果是,是第几项
解:(1)由a 1 = -1,公差 d = -3,n =20,
a20 =8 + (20 - 1) ×(-3)= -49
(2)由a 1 = -1,公差 d = -4,得数列的通项公式为
a n = - 5 -4 ( n-1 )
由 - 401 = - 5 -4 ( n-1 )
∴ n = 100
即- 401是这个数列的第 100项
例2、在等差数列{ a n }中,已知a5=10 , a12 =31,求a1、d、 a20、an .
解:∵ a5=10 , a12 =31,则
a1+4d = 10
a1+11d = 31
a1= - 2
d = 3
∴an =a1+(n - 1)d=3n - 5
a20 =a1+(20 - 1)d=55
例3 梯子最高一级宽33cm,最低一级宽为110cm,中间还有10级,各级的宽度成等差数列,计算中间各级的宽度。
解:设{ a n }表示梯子自上而下各级宽度所成的等差数列。
由已知条件,
可知: a 1 =33, a 12 =110, n=12
∴ a 12 = a1+(12 - 1)d,即10=33+11 d
解得d=7
因此, a 2 =40, a 3 =47
…
答:梯子…
例4已知数列{ a n }的通项公式a n =pn+q,其中 p、q是常数,那么这个数列是否一定是等差数列?若是,首项与公差分别是什么?
分析:由等差数列的定义,要判定{ a n }是不是等差数列,只要看a n -a n -1 ( n ≥ 2 )是不是一个与n无关的常数。
解:当n ≥ 2时
a n -a n -1 = pn+q - [p(n - 1) +q]= p
这是一个与n无关的常数,所以数列{ a n }是等差数列,首项为p+q,公差为p。
注:(1)若p=0,则{ a n }为公差为0的等差数列,即为常数列q , q , q , …
(2)若p≠0,则a n 是关于n的一次函数,
图象特点是表示数列的各点均在一次函数y =px+q的图象上,一次项的系数是公差。
(3)数列{ a n }为等差数列的充要条件是其通项a n =pn+q( p、q是常数)
观察下列数列:
(1) 6,3,0,-3,-6,-9,…
(2) 1,11,21,31,41,…
(3) 1,1,1,1,…
请同学们仔细观察,看看以上三个数列有什么共同的特征?
共同特征:从第二项起,每一项与它前面一项的差等于同一个常数。
我们给具有这种特征的数列一个名字------等差数列
定义:如果一个数列从第 ___ 项起,每一项与它的 ___ __的差等于 _____ 一常数 d,这个数列叫做 __________ ,d 为此数列的 __________。
二
前一项
同
等差数列
公差
问题1:由数列的前几项(有限项)按定义作差都为同一常数,能否说明此数列为等差数列?
不能
问题2:公差d一定是由 项减 项所得。
后
前
问题3:判断数列为等差数列的方法:
a n -a n -1 = d ( n ≥ 2 )
或 a n + 1 -a n = d ( n ≥ 1 )
等差数列的通项公式如何求?
设等差数列 { a n }的公差为 d ,则有
a n -a n -1 = ____
a 2 -a 1 = _____
a 3 -a 2 = _____
a 4 -a 3 = _____
……
+ )
d
d
d
d
n-1个
a n -a 1 = ( n-1 ) d
—— 递推求和法
设等差数列 { a n }的公差为 d ,则有
a 2 = a 1 + ____
d
a 3 = a 2 + __ = a 1 + ___
d
2d
a 4 = a 3 + __ = a 1 + ___
d
3d
……
a n = a n -1 + _____ = a 1 + ______
d
(n-1)d
即:a n = a 1 + (n-1)d
—— 猜想论证法
等差数列的通项公式:
若等差数列 { a n } 的首项为 a 1,公差为 d ,则通项公式为
a n = a 1 + ( n-1 ) d,n ∈N +
等差数列中,a n 是 n 的 ____________,
图象特点 _________________________
一次函数
直线上的一些有规律的点
或 a n 是常数函数,公差为 d = _______
0
例1.(1)求等差数列8 , 5 , 2 ,…的第20项.
(2) - 401是不是等差数列- 5, - 9, - 13, …的项 如果是,是第几项
解:(1)由a 1 = -1,公差 d = -3,n =20,
a20 =8 + (20 - 1) ×(-3)= -49
(2)由a 1 = -1,公差 d = -4,得数列的通项公式为
a n = - 5 -4 ( n-1 )
由 - 401 = - 5 -4 ( n-1 )
∴ n = 100
即- 401是这个数列的第 100项
例2、在等差数列{ a n }中,已知a5=10 , a12 =31,求a1、d、 a20、an .
解:∵ a5=10 , a12 =31,则
a1+4d = 10
a1+11d = 31
a1= - 2
d = 3
∴an =a1+(n - 1)d=3n - 5
a20 =a1+(20 - 1)d=55
例3 梯子最高一级宽33cm,最低一级宽为110cm,中间还有10级,各级的宽度成等差数列,计算中间各级的宽度。
解:设{ a n }表示梯子自上而下各级宽度所成的等差数列。
由已知条件,
可知: a 1 =33, a 12 =110, n=12
∴ a 12 = a1+(12 - 1)d,即10=33+11 d
解得d=7
因此, a 2 =40, a 3 =47
…
答:梯子…
例4已知数列{ a n }的通项公式a n =pn+q,其中 p、q是常数,那么这个数列是否一定是等差数列?若是,首项与公差分别是什么?
分析:由等差数列的定义,要判定{ a n }是不是等差数列,只要看a n -a n -1 ( n ≥ 2 )是不是一个与n无关的常数。
解:当n ≥ 2时
a n -a n -1 = pn+q - [p(n - 1) +q]= p
这是一个与n无关的常数,所以数列{ a n }是等差数列,首项为p+q,公差为p。
注:(1)若p=0,则{ a n }为公差为0的等差数列,即为常数列q , q , q , …
(2)若p≠0,则a n 是关于n的一次函数,
图象特点是表示数列的各点均在一次函数y =px+q的图象上,一次项的系数是公差。
(3)数列{ a n }为等差数列的充要条件是其通项a n =pn+q( p、q是常数)
