苏科版七年级下册11.5用一元一次不等式解决问题课件(16张ppt)
文档属性
| 名称 | 苏科版七年级下册11.5用一元一次不等式解决问题课件(16张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 714.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-20 15:56:12 | ||
图片预览





文档简介
(共16张PPT)
11.5
用一元一次不等式
解决问题
初中数学七年级下册
(苏科版)
一只纸箱质量为1kg,当放入一些苹果(每个苹果的质量为0.25kg)后,箱子和苹果的总质量不超过10kg.这只纸箱内最多能装多少个苹果?
解:设最多能装x个苹果
根据题意可得:
1+0.25x≤10
某人骑一辆电动自行车,如果行驶速度增加5km/h,那么2h所行驶的路程不少于原来速度2.5h所行驶的路程.他原来行驶的速度最大是多少?
解:设原来的行驶速度为xkm/h
则:2(x+5)≥2.5x
……
小明有1元和5角的硬币共13枚,这些硬币的总币值小于8.5元。问小明可能有几枚1元的硬币?
解:设小明有1元的硬币x枚
则:
x+0.5(13-x)<8.5
……
你是如何设未知数的?
列不等式解应用题基本步骤是什么?
列一元一次不等式解决问题的一般步骤:
1.认真审题,分清已知量、未知量及其关系,找出题中不等关系,要抓住题设中的关键字“眼”,如“大于”、“小于”、“不小于”、“不大于”等的含义.
2.设出适当的未知数.
3.根据题中的不等关系,列出不等式.
4.解出所列不等式的解集.
5.写出答案,并检验答案是否符合题意.
审
设
列
解
答
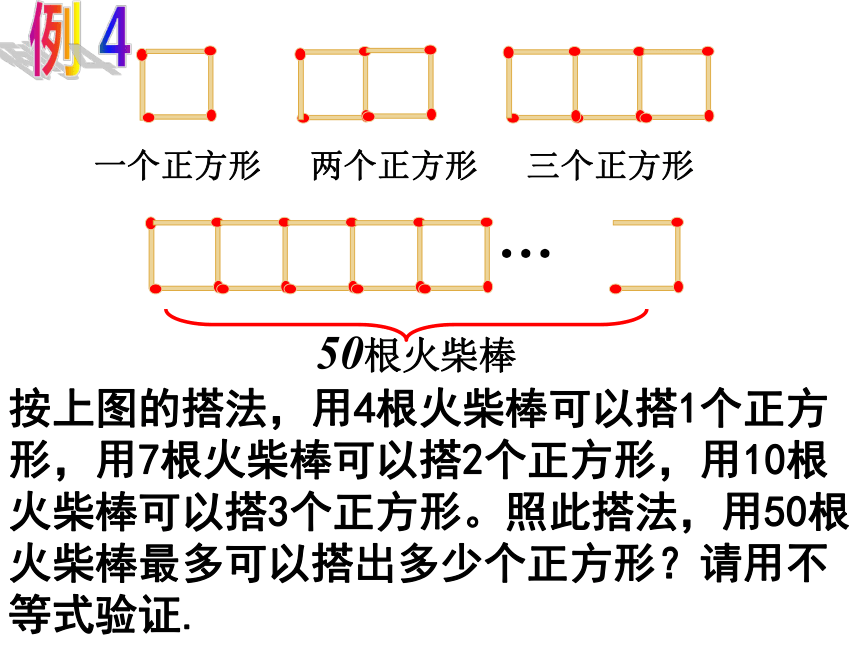
按上图的搭法,用4根火柴棒可以搭1个正方形,用7根火柴棒可以搭2个正方形,用10根火柴棒可以搭3个正方形。照此搭法,用50根火柴棒最多可以搭出多少个正方形?请用不等式验证.
某电影院暑假向学生优惠开放,每张票2元.另外,每场次还将售出每张5元的普通票300张,如果要保持每场次票房收入不低于2000元,那么平均每场次至少应出售学生优惠票多少张?
解:设至少应售出学生优惠票x张
则
2x+5×300≥2000
解得:x≥250
水果店进了某种水果1t,进价是7元/kg.售价定为10元/kg,销售一半以后,为了尽快售完,准备打折出售.如果要使总利润不低于2000元,那么余下的水果可以按原定价的几折出售?
解:设可以按原定的x折出售
则500×(10-7)+500(x-7)≥2000
解得:x≥8
某高速公路工地需要实施爆破,操作人员点燃导火线后,要在炸药爆炸前跑到400米以外的安全区域.已知导火线的燃烧速度是1.2厘米/秒,人跑步的速度是5米/秒.问导火线至少需要多长?
解得x≥96
某公司到果园基地地购买某种水果,慰问医务工作者.果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案;每千克9元,由基地送货上门;乙方案:每千克8元,由顾客自己租车运回.已知该公司租车从基地到公司的运输费为5000元.试问:当购买量在什么范围时,选择哪种购买方案付款最少?并说明理由.
解:设购买x千克时甲方案付款少(其中x≥3000)
则
9x<8x+5000
解得x<5000
∴当3000≦x<5000时,甲方案付款最少
x=5000时,甲、乙两种方案付款一样多
5000<x时,乙方案付款最少
某服装厂生产一种西装和领带,西装每套定价200元领带每条定价40元.厂方在开展促销活动期间,向客户提供两种优惠方案:(1)买一套西装送一条领带;(2)西装和领带均按定价的90%付款.某商店老板现要到该服装厂购买西装20套,领带x(x>20)条.请你根据x的不同情况,帮助商店老板选择最省钱的购买方案.
解:设买x条领带时方案一比较省钱
则
200×20+40(x-20)<(200×20+40x)90%
解得:x<100
∴当20<x<100时,方案一付款最少
x=100时,两种方案付款一样多
100<x时,方案二付款最少
【小结】
1.一元一次不等式解决问题有哪些步骤?
2.用一元一次不等式解决问题的关键是什么?
3.通过这节课的学习,你还有什么感受?一起分享!
2.
思考题(选做):
有人问一位数学老师,她所教的班级有多少个学生,这位老师风趣地说:“一半在学数学,四分之一在学音乐,七分之一在读英语,还剩不足6位同学在操场上踢足球”.试问这个班共有多少学生?
【课后作业】
1.《数学补充习题》11.5 用一元一次
不等式解决问题.
11.5
用一元一次不等式
解决问题
初中数学七年级下册
(苏科版)
一只纸箱质量为1kg,当放入一些苹果(每个苹果的质量为0.25kg)后,箱子和苹果的总质量不超过10kg.这只纸箱内最多能装多少个苹果?
解:设最多能装x个苹果
根据题意可得:
1+0.25x≤10
某人骑一辆电动自行车,如果行驶速度增加5km/h,那么2h所行驶的路程不少于原来速度2.5h所行驶的路程.他原来行驶的速度最大是多少?
解:设原来的行驶速度为xkm/h
则:2(x+5)≥2.5x
……
小明有1元和5角的硬币共13枚,这些硬币的总币值小于8.5元。问小明可能有几枚1元的硬币?
解:设小明有1元的硬币x枚
则:
x+0.5(13-x)<8.5
……
你是如何设未知数的?
列不等式解应用题基本步骤是什么?
列一元一次不等式解决问题的一般步骤:
1.认真审题,分清已知量、未知量及其关系,找出题中不等关系,要抓住题设中的关键字“眼”,如“大于”、“小于”、“不小于”、“不大于”等的含义.
2.设出适当的未知数.
3.根据题中的不等关系,列出不等式.
4.解出所列不等式的解集.
5.写出答案,并检验答案是否符合题意.
审
设
列
解
答
按上图的搭法,用4根火柴棒可以搭1个正方形,用7根火柴棒可以搭2个正方形,用10根火柴棒可以搭3个正方形。照此搭法,用50根火柴棒最多可以搭出多少个正方形?请用不等式验证.
某电影院暑假向学生优惠开放,每张票2元.另外,每场次还将售出每张5元的普通票300张,如果要保持每场次票房收入不低于2000元,那么平均每场次至少应出售学生优惠票多少张?
解:设至少应售出学生优惠票x张
则
2x+5×300≥2000
解得:x≥250
水果店进了某种水果1t,进价是7元/kg.售价定为10元/kg,销售一半以后,为了尽快售完,准备打折出售.如果要使总利润不低于2000元,那么余下的水果可以按原定价的几折出售?
解:设可以按原定的x折出售
则500×(10-7)+500(x-7)≥2000
解得:x≥8
某高速公路工地需要实施爆破,操作人员点燃导火线后,要在炸药爆炸前跑到400米以外的安全区域.已知导火线的燃烧速度是1.2厘米/秒,人跑步的速度是5米/秒.问导火线至少需要多长?
解得x≥96
某公司到果园基地地购买某种水果,慰问医务工作者.果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案;每千克9元,由基地送货上门;乙方案:每千克8元,由顾客自己租车运回.已知该公司租车从基地到公司的运输费为5000元.试问:当购买量在什么范围时,选择哪种购买方案付款最少?并说明理由.
解:设购买x千克时甲方案付款少(其中x≥3000)
则
9x<8x+5000
解得x<5000
∴当3000≦x<5000时,甲方案付款最少
x=5000时,甲、乙两种方案付款一样多
5000<x时,乙方案付款最少
某服装厂生产一种西装和领带,西装每套定价200元领带每条定价40元.厂方在开展促销活动期间,向客户提供两种优惠方案:(1)买一套西装送一条领带;(2)西装和领带均按定价的90%付款.某商店老板现要到该服装厂购买西装20套,领带x(x>20)条.请你根据x的不同情况,帮助商店老板选择最省钱的购买方案.
解:设买x条领带时方案一比较省钱
则
200×20+40(x-20)<(200×20+40x)90%
解得:x<100
∴当20<x<100时,方案一付款最少
x=100时,两种方案付款一样多
100<x时,方案二付款最少
【小结】
1.一元一次不等式解决问题有哪些步骤?
2.用一元一次不等式解决问题的关键是什么?
3.通过这节课的学习,你还有什么感受?一起分享!
2.
思考题(选做):
有人问一位数学老师,她所教的班级有多少个学生,这位老师风趣地说:“一半在学数学,四分之一在学音乐,七分之一在读英语,还剩不足6位同学在操场上踢足球”.试问这个班共有多少学生?
【课后作业】
1.《数学补充习题》11.5 用一元一次
不等式解决问题.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
