2009学年第一学期徐汇区初二年级数学学科学习能力诊断卷
文档属性
| 名称 | 2009学年第一学期徐汇区初二年级数学学科学习能力诊断卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 77.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-21 00:00:00 | ||
图片预览

文档简介
2009学年第一学期徐汇区初二年级数学学科
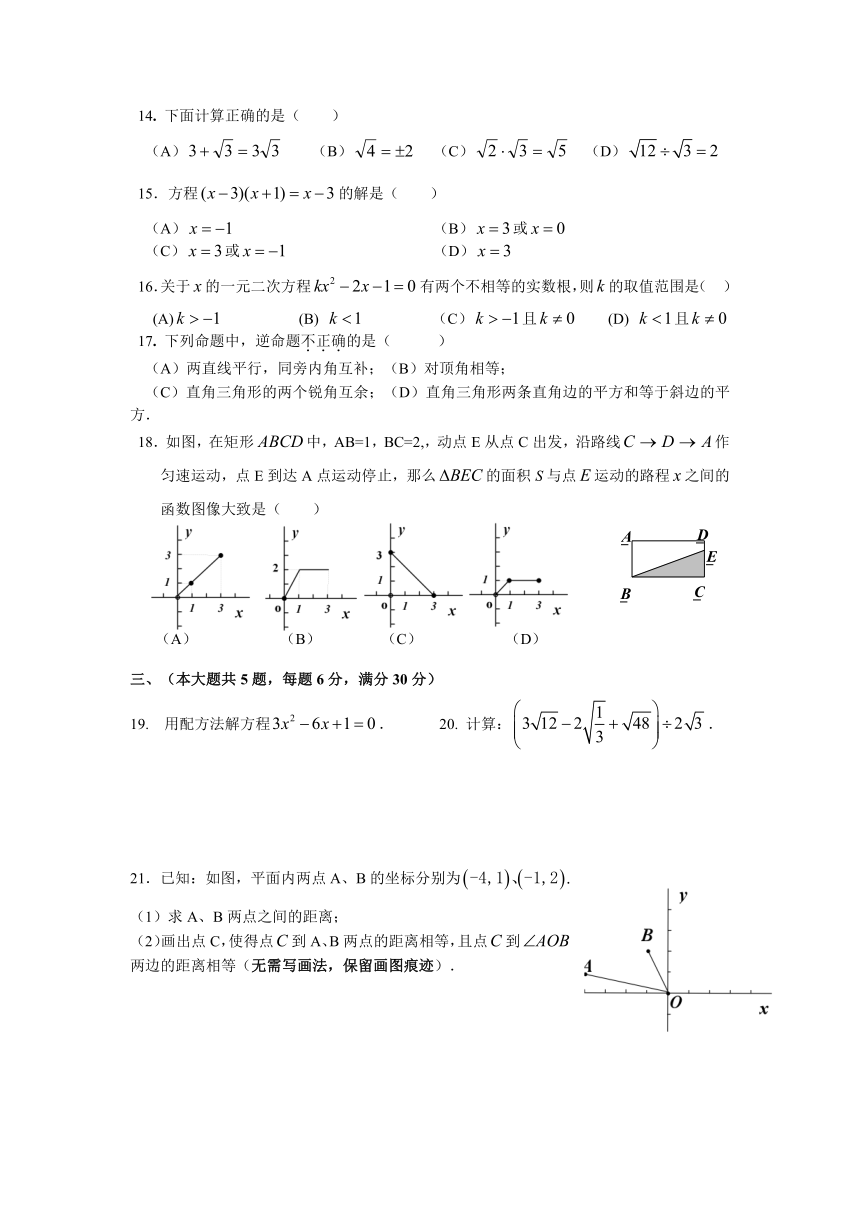
学习能力诊断卷
(90分钟完卷,满分100分) 2010.1
题号 一 二 三 四 五 总分
19 20 21 22 23 24 25 26
得分
一、填空题(本大题共13题,每题2分,满分26分)
1.计算:=_________.
2.计算:= .
3.方程的根是 .
4.在实数范围内分解因式:________________.
5.某旅游景点6月份共接待游客25万人次,由于暑期放假学生旅游人数猛增,8月份共接待游客64万人次,如果每月的增长率都为,则根据题意可列方程 _.
6.已知函数,那么__________.
7.函数的自变量的取值范围是__________.
8.正比例函数的图像经过第 象限.
9.已知反比例函数的图像在每个象限内的值随的值增大而减小,则的取值范围是 .
10.平面上到点的距离为3cm的点的轨迹是__________ _______.
11.如图,长为4m的梯子搭在墙上与地面成60°角,则梯子的顶端离地面的高度为
(结果保留根号).
12.中,,,,则的面积是___________.
13.如图,在ΔABC中,∠C=90°,∠ABC的平分线BD交AC于点D,若BD=13厘米,BC=12厘米,则点D到直线AB的距离是__________厘米.
二、选择题(本大题共5题,每题2分,满分10分)
14. 下面计算正确的是( )
(A) (B) (C) (D)
15.方程的解是( )
(A) (B)或
(C)或 (D)
16.关于的一元二次方程有两个不相等的实数根,则的取值范围是( )
(A) (B) (C)且 (D) 且
17. 下列命题中,逆命题不正确的是( )
(A)两直线平行,同旁内角互补;(B)对顶角相等;
(C)直角三角形的两个锐角互余;(D)直角三角形两条直角边的平方和等于斜边的平方.
18.如图,在矩形中,AB=1,BC=2,,动点E从点C出发,沿路线作
匀速运动,点E到达A点运动停止,那么的面积S与点运动的路程之间的
函数图像大致是( )
三、(本大题共5题,每题6分,满分30分)
19. 用配方法解方程. 20. 计算:.
21.已知:如图,平面内两点A、B的坐标分别为
(1)求A、B两点之间的距离;
(2)画出点C,使得点到A、B两点的距离相等,且点到两边的距离相等(无需写画法,保留画图痕迹).
22.某天小明骑自行车上学,学校离家3000千米,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校. 右图描述的是他离家的距离和离家的时间之间的函数图像,根据图像解决下列问题:
(1) 自行车发生故障时离家距离为 米;
(2) 到达学校时共用时间 分钟;
(3) 修车时间为 分钟;
(4) 自行车发生故障前他的速度是每分钟 米;
(5)自行车故障排除后他的速度是每分钟 米.
23. 已知:如图,∠BAC=∠ABD ,AC=BD,点O是AD、BC的交点,点E是AB的中点.
证明:OE⊥AB.
四、(本大题共3题,每题8分,满分24分)
24.利用25米长的墙为一边,用篱笆围成一个长方形菜地,并在中间用篱笆分割成三个面积相等的小长方形,总共用去篱笆48米。 如果围成的菜地面积是128米2,求菜地的宽AB。
25. 已知: 如图,在中,AD是高,CE是AB边上的中线,且DC=BE.
求证:∠B=2∠BCE.
26.如图,将一个长方形放置在平面直角坐标系中,,E是AB的中点,反比例函数图像过点E且和BC相交于点F.
(1)求直线OB和反比例函数的解析式;
(2)求四边形OEBF的面积.
五、(第(1)4分、第(2)小题6分,满分10分)
27.已知:三角形纸片ABC中,,AB = 12,BC =6,是边AC上一点.将三角形纸片折叠,使点B与点重合,折痕与BC、AB分别相交于E、F.
(1)设BE = ,B’C =,试建立关于的函数关系式,并直接写出x的取值范围;
(2)当△AFB’是直角三角形时,求出x的值.
第13题图
第11题
(A) (B) (C) (D)
_
E
_
D
_
C
_
B
_
A
离家时间(分钟)
离家的距离(米)
10 15 20
3000
1500
O
A
B
C
学习能力诊断卷
(90分钟完卷,满分100分) 2010.1
题号 一 二 三 四 五 总分
19 20 21 22 23 24 25 26
得分
一、填空题(本大题共13题,每题2分,满分26分)
1.计算:=_________.
2.计算:= .
3.方程的根是 .
4.在实数范围内分解因式:________________.
5.某旅游景点6月份共接待游客25万人次,由于暑期放假学生旅游人数猛增,8月份共接待游客64万人次,如果每月的增长率都为,则根据题意可列方程 _.
6.已知函数,那么__________.
7.函数的自变量的取值范围是__________.
8.正比例函数的图像经过第 象限.
9.已知反比例函数的图像在每个象限内的值随的值增大而减小,则的取值范围是 .
10.平面上到点的距离为3cm的点的轨迹是__________ _______.
11.如图,长为4m的梯子搭在墙上与地面成60°角,则梯子的顶端离地面的高度为
(结果保留根号).
12.中,,,,则的面积是___________.
13.如图,在ΔABC中,∠C=90°,∠ABC的平分线BD交AC于点D,若BD=13厘米,BC=12厘米,则点D到直线AB的距离是__________厘米.
二、选择题(本大题共5题,每题2分,满分10分)
14. 下面计算正确的是( )
(A) (B) (C) (D)
15.方程的解是( )
(A) (B)或
(C)或 (D)
16.关于的一元二次方程有两个不相等的实数根,则的取值范围是( )
(A) (B) (C)且 (D) 且
17. 下列命题中,逆命题不正确的是( )
(A)两直线平行,同旁内角互补;(B)对顶角相等;
(C)直角三角形的两个锐角互余;(D)直角三角形两条直角边的平方和等于斜边的平方.
18.如图,在矩形中,AB=1,BC=2,,动点E从点C出发,沿路线作
匀速运动,点E到达A点运动停止,那么的面积S与点运动的路程之间的
函数图像大致是( )
三、(本大题共5题,每题6分,满分30分)
19. 用配方法解方程. 20. 计算:.
21.已知:如图,平面内两点A、B的坐标分别为
(1)求A、B两点之间的距离;
(2)画出点C,使得点到A、B两点的距离相等,且点到两边的距离相等(无需写画法,保留画图痕迹).
22.某天小明骑自行车上学,学校离家3000千米,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校. 右图描述的是他离家的距离和离家的时间之间的函数图像,根据图像解决下列问题:
(1) 自行车发生故障时离家距离为 米;
(2) 到达学校时共用时间 分钟;
(3) 修车时间为 分钟;
(4) 自行车发生故障前他的速度是每分钟 米;
(5)自行车故障排除后他的速度是每分钟 米.
23. 已知:如图,∠BAC=∠ABD ,AC=BD,点O是AD、BC的交点,点E是AB的中点.
证明:OE⊥AB.
四、(本大题共3题,每题8分,满分24分)
24.利用25米长的墙为一边,用篱笆围成一个长方形菜地,并在中间用篱笆分割成三个面积相等的小长方形,总共用去篱笆48米。 如果围成的菜地面积是128米2,求菜地的宽AB。
25. 已知: 如图,在中,AD是高,CE是AB边上的中线,且DC=BE.
求证:∠B=2∠BCE.
26.如图,将一个长方形放置在平面直角坐标系中,,E是AB的中点,反比例函数图像过点E且和BC相交于点F.
(1)求直线OB和反比例函数的解析式;
(2)求四边形OEBF的面积.
五、(第(1)4分、第(2)小题6分,满分10分)
27.已知:三角形纸片ABC中,,AB = 12,BC =6,是边AC上一点.将三角形纸片折叠,使点B与点重合,折痕与BC、AB分别相交于E、F.
(1)设BE = ,B’C =,试建立关于的函数关系式,并直接写出x的取值范围;
(2)当△AFB’是直角三角形时,求出x的值.
第13题图
第11题
(A) (B) (C) (D)
_
E
_
D
_
C
_
B
_
A
离家时间(分钟)
离家的距离(米)
10 15 20
3000
1500
O
A
B
C
同课章节目录
