6.1-3复习

(共12张PPT)
1、表格法：
我们已经学习了几种表示变量之间关系的方法？
2、关系式法(解析式法)：
3、图象法
能直观反映变量间的整体变化情况
及变化规律
直接显示数据
方便计算
在用图象表示变量之间的关系时，通常用水平方向的数轴（称为横轴）上的点表示自变量，用竖直方向的数轴（称为纵轴）上的点表示因变量。
在用关系式法表示变量之间的关系时应写成y=ax+b的形式，即因变量=？？？？的形式。
小明帮助母亲算了4月份的用水量，小明记录了4月初连续8天每天早上水表显示的读数，列成的表格如下：（单位：m ）
日期 1 2 3 4 5 6 7 8
水表显示 45 47 48 50 53 55 57 59
1、这个表格反映哪两个变量之间的关系？哪个是自
变量？哪个是因变量？
2、4月5日早上水表的读数是多少？
3、这个月的前5天共用水多少？
4、估计在4月9日早上水表的读数是多少？
表格法：
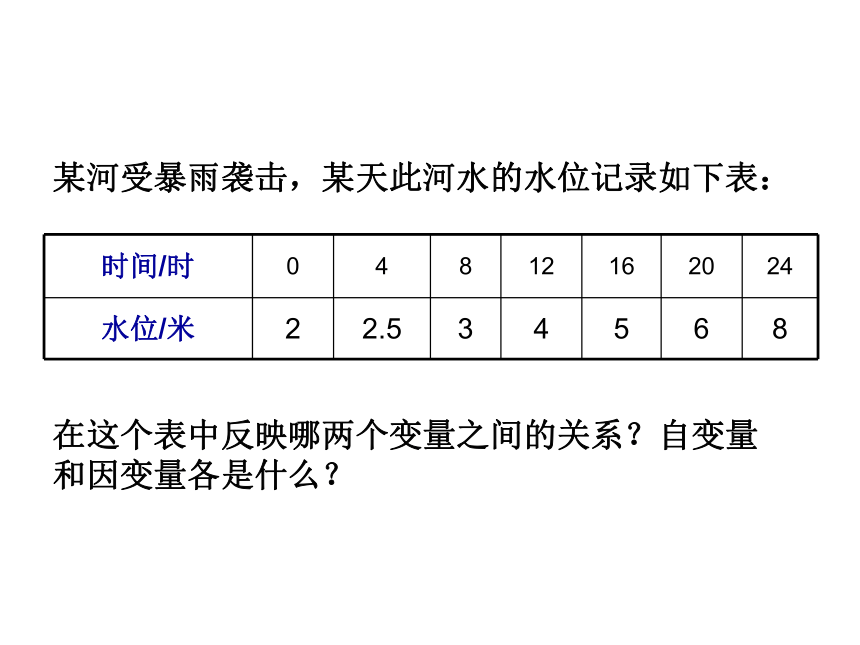
某河受暴雨袭击，某天此河水的水位记录如下表：
时间/时 0 4 8 12 16 20 24
水位/米 2 2.5 3 4 5 6 8
在这个表中反映哪两个变量之间的关系？自变量和因变量各是什么？
2、有一颗小树苗，刚栽下去时树高时2.1米，以后每年长0.3米。
（1）上述的哪些量在发生变化？自变量和因变量各是什么？
（2）3年后树高是多少？
（3）如果我们只知道树苗栽下去时的树高为2.1米，它每年的生长速度是均匀的，又测出两年后树苗高3.3米，那么5年后树高是多少米？
想一想
A
B
C
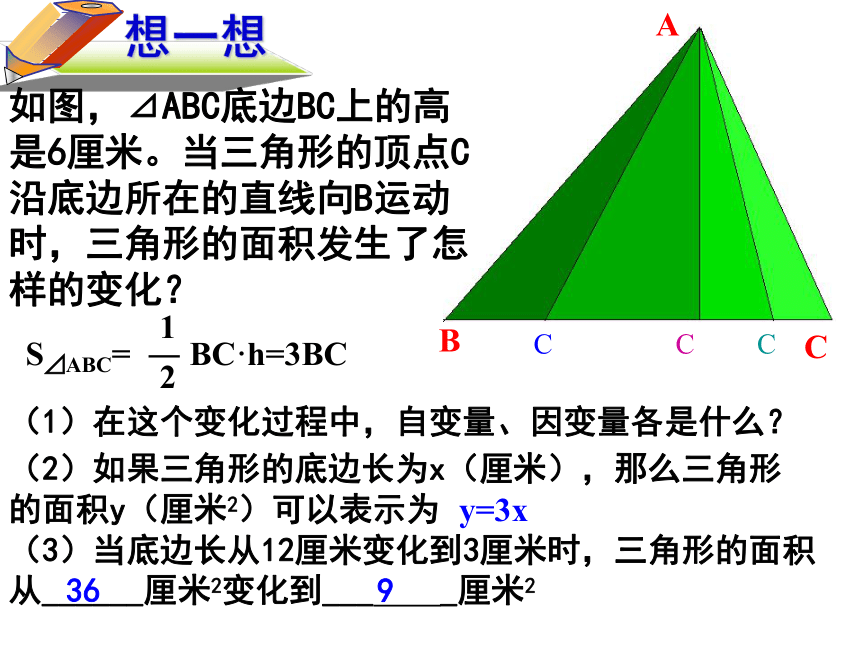
如图，⊿ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在的直线向B运动时，三角形的面积发生了怎样的变化？
C
C
S⊿ABC= ― BC·h=3BC
1
2
C
（1）在这个变化过程中，自变量、因变量各是什么？
（2）如果三角形的底边长为x（厘米），那么三角形的面积y（厘米2）可以表示为　　　　　　　
y=3x
（3）当底边长从12厘米变化到3厘米时，三角形的面积从______厘米2变化到___　　_厘米2
36
9
2．如图所示，梯形上底的长是 x，下底的长是 15， 高是 8。
（1）梯形面积 y 与上底长 x 之间的关系式是什么？
（2）用表格表示当 x 从 10 变到 20 时（每次增加1），y 的相应值；
（3）当 x 每增加 1 时，y如何变化？说说理由;
（4）当 x ＝0时，y 等于什么？此时它表示的什么？
x
8
15
3.将长为20cm,宽为10 cm的长方形白纸，按图的方法粘合起来，粘合部分的宽为3cm,当粘合的白纸数增加时粘合后的总长度也在变化。
（1）在这个变化过程中，自变量、因变量各是什么？
（2）若粘合的白纸数为x（张），则粘合后的总长度y（cm）间的关系式是什么？
（3）当从5张变到7张时，总长度怎么变化？
2、判断。（对的打“ √”，错的打“×”）
计划购买乒乓球50元，求所购买的总数n（个）与单价a（元）的关系。
(1) 关系式为：a =
50
n
( )
(2)关系式为：an = 50
( )
(3)关系式为：n =
50
a
( )
×
×
没有分清哪一个是因变量
没有将因变量单独放在等号左边
√
常见的思维误区：（1）变化关系式写得不正确；
（2）变化关系式没有将因变量单
独放在等号左边；
温度/ C
请根据下图,与同学讨论某地某天的温度变化情况.
(1)上午9时的温度是____,
12时呢
(2)这一天的最高温度是___,
是____时达到的, 最低温
度呢
(3)这一天的温差是____,
从最低温度到最高温度经
过____小时.
27
31
14 C
M
D
N
27 C
31 C
37
15
E
37 C
15
23
23 C
3
3时
12
温度/ C
请根据下图,与同学讨论某地某天的温度变化情况.
(4)在什么时间范围内温度在
上升 在什么时间范围内温
度在下降
(5)图中的A点表示的是什么
B点呢
(6)你能预测次日凌晨1时的温度吗 说说你的理由.
D
E
F
3时到15时
0时到3时、15到24时
21时的温度是310C
0时的温度是260C
大约是240C左右
下面是某港口“水上游乐场”从0时到12时的水深情况变化图：
水深/米
时间/时
你能从图
中获得哪些
信息？
若规定水深超过6米时，不允许游客下海，图中有哪些时间段可以下海？
2.5
7.5