六年级上册数学课件-第九单元第4课时 圆 人教版(共22张PPT)
文档属性
| 名称 | 六年级上册数学课件-第九单元第4课时 圆 人教版(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 10.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-20 21:13:39 | ||
图片预览

文档简介
总复习
圆
9
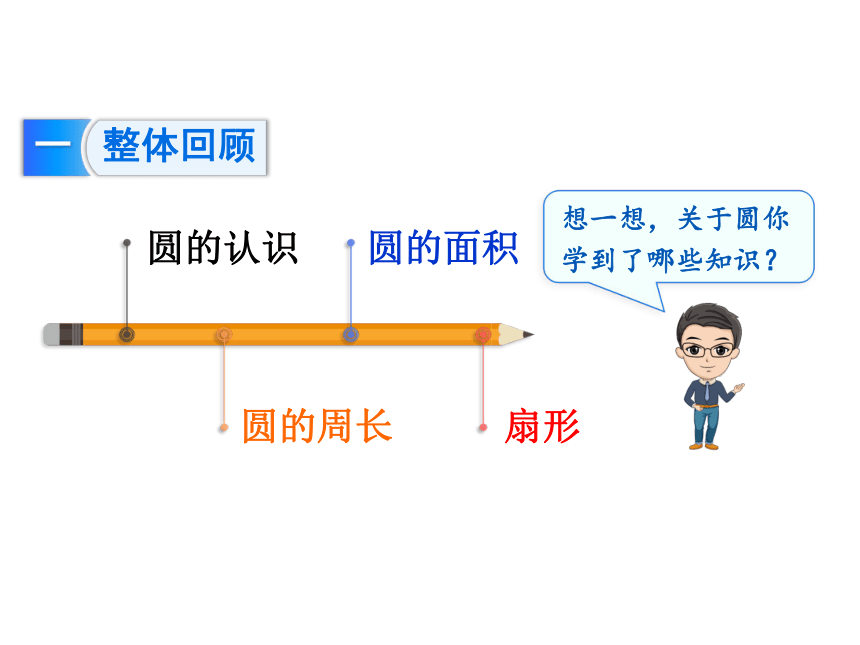
整体回顾
想一想,关于圆你学到了哪些知识?
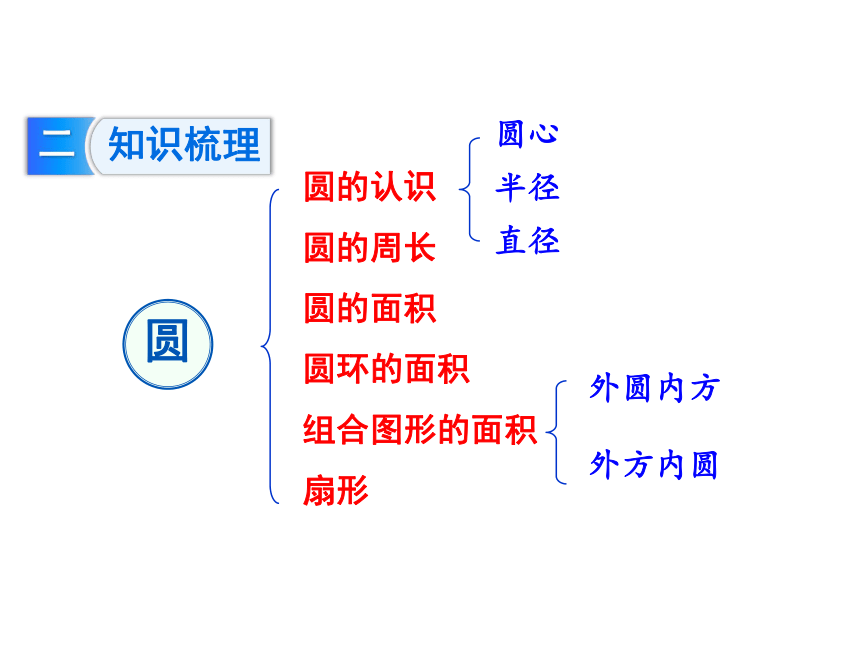
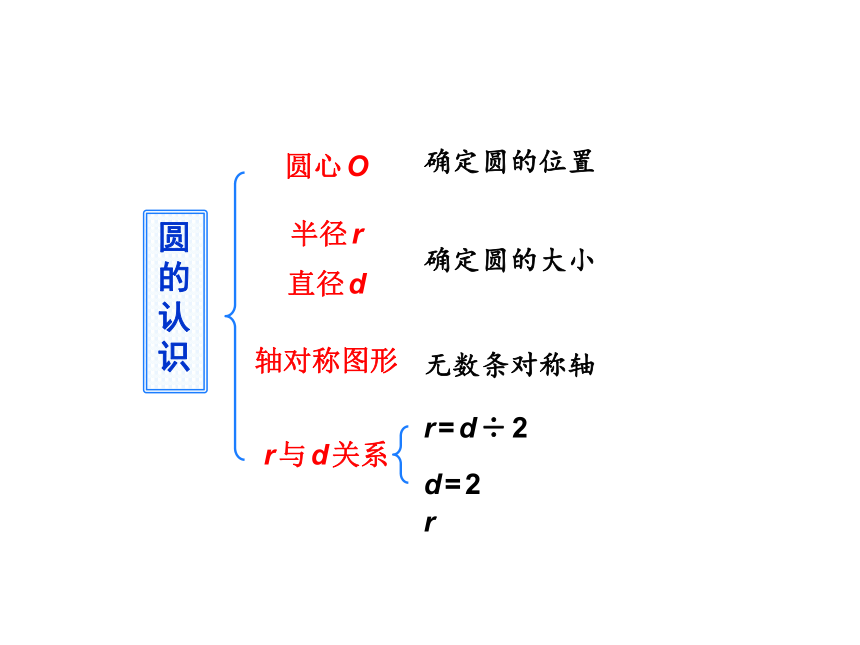
圆的认识
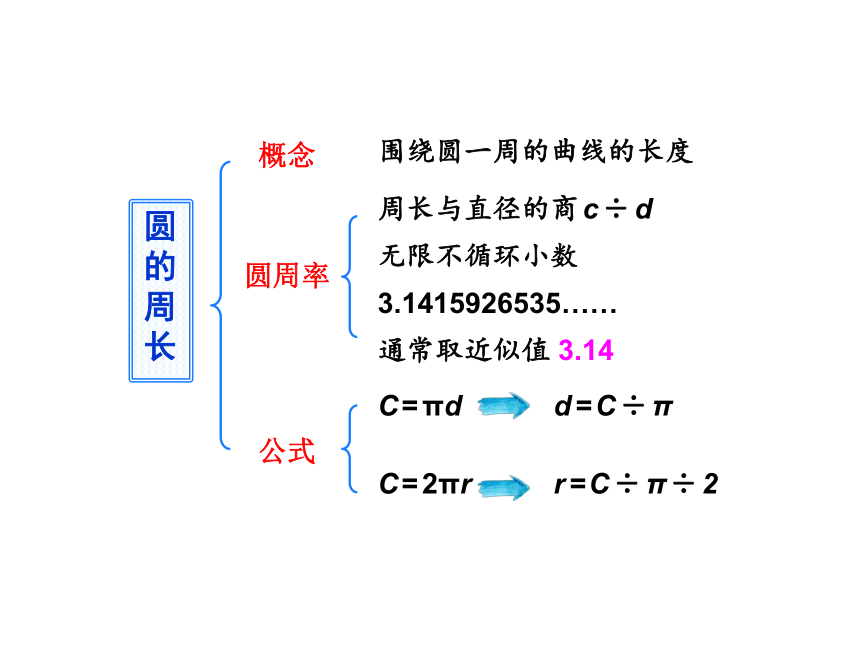
圆的周长
圆的面积
扇形
知识梳理
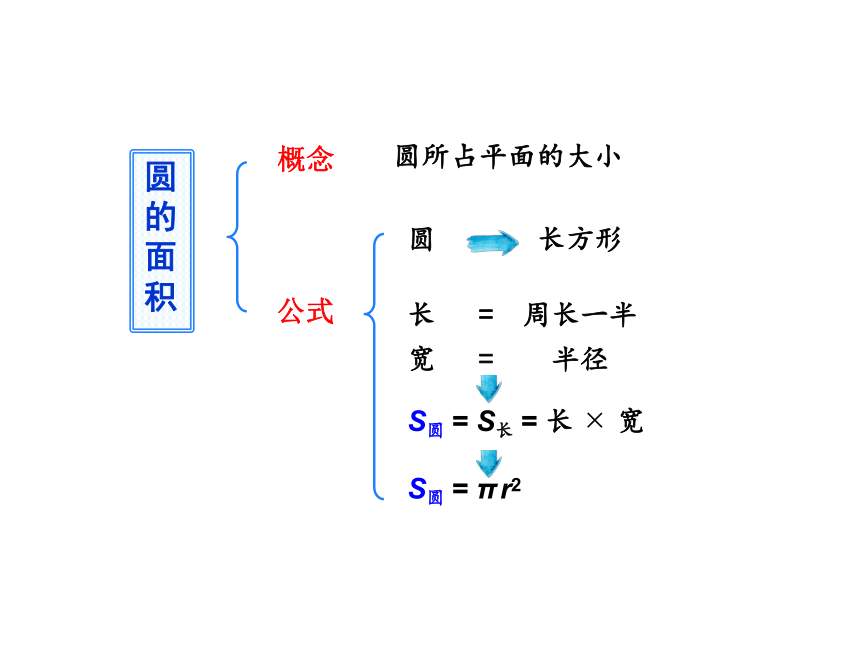
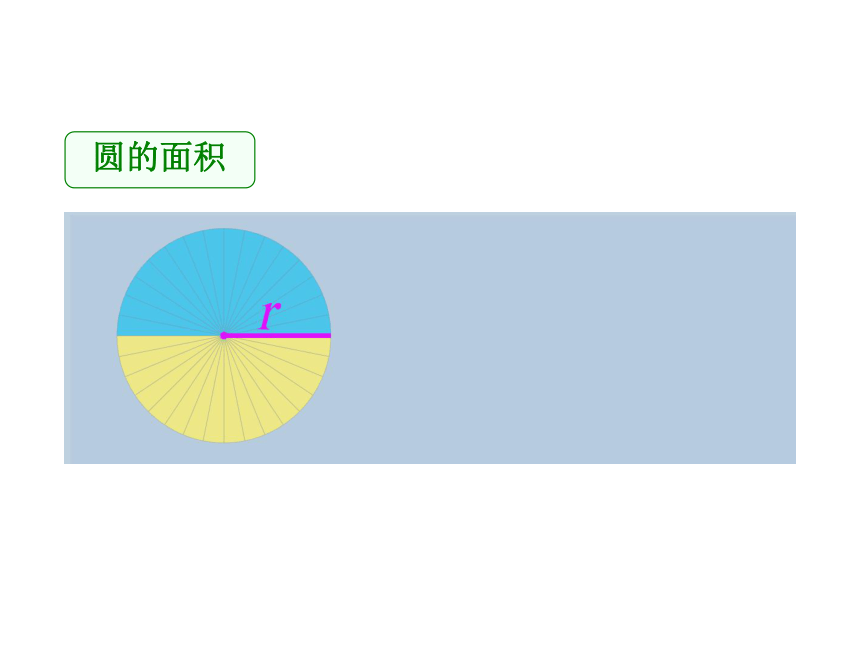
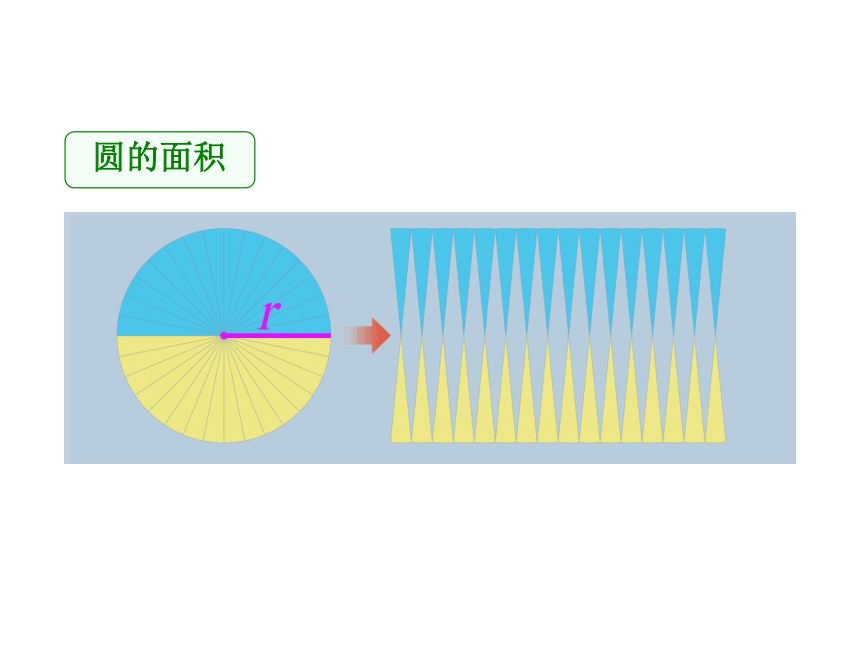
圆的面积
圆的面积
圆的面积
r
C=2πr
用S表示圆的面积,圆的面积计算公式就是:
S=πr?
圆的面积
扇形
O
弧
A
半径
半径
B
图上A、B两点之间的部分叫做弧,读作“弧AB”。
扇形
O
弧
A
半径
半径
B
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
扇形
O
弧
圆心角
A
半径
半径
B
顶点在圆心的角叫做圆心角。
一个公园是圆形布局,半径长1km,圆心处设立了一个纪念碑。公园共有四个门,每两个相邻的门之间有一条直的水泥路相通,长约1.41km。
(1)这个公园的围墙有多长?
C=2πr
= 6.28(km)
= 2×3.14×1
答:这个公园的围墙长6.28千米。
西门
南门
东门
小湖
纪念碑
北门
随堂练习
(教科书113页第4题)
= 2(km)
1+1
答:北门在南门的正北方向,
距离南门有2千米。
西门
南门
东门
小湖
纪念碑
北门
(2)北门在南门的什么方向?距离南门多远?
西门
南门
东门
小湖
纪念碑
北门
(3)如果公园里有一个半径为0.2km的圆形小湖,
这个公园的陆地面积是多少平方千米?
3.14×12?3.14×0.22
= 3.0144(km2)
答:这个公园的陆地面积
是3.0144平方千米。
西门
南门
东门
小湖
纪念碑
北门
(4)请你再提出一些数学问题并试着解决。
2?1.41=0.59(千米)
答:东门到西门的距离比东门
到南门远0.59千米。
答案不唯一。
如:东门到西门的距离比东门到
南门远多少千米?
综合运用
1.填空题。
一个圆的直径是2m,它的周长是( ) m,面积是( ) m2。
已知圆的周长,求d=( ),求r=( )。
圆的半径扩大3倍,直径就扩大( )倍,周长就扩大( )倍,面积就扩大( )倍。
6.28
3.14
3
3
9
7000÷(3.14×0.6×120)
≈31(分钟)
答:他经过这个大桥大约要31分钟。
一辆自行车的外轮直径是0.6m,如果小明骑车平均每分钟转120圈,他经过7000m的大桥要几分钟?(得数保留整数)
2.
=1.2(m)
4.8÷4
正方形边长:
剪下来的面积:
1.2×1.2?3.14×(1.2÷2)2
= 1.22?3.14×0.62
= 1.44?1.1304
= 0.3096(平方米)
答:剪下来的纸的面积是0.3096平方米。
在一个周长为4.8m的正方形纸片内,要剪一个最大的圆,剪下来的纸的面积是多少平方米?
3.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
圆
9
整体回顾
想一想,关于圆你学到了哪些知识?
圆的认识
圆的周长
圆的面积
扇形
知识梳理
圆的面积
圆的面积
圆的面积
r
C=2πr
用S表示圆的面积,圆的面积计算公式就是:
S=πr?
圆的面积
扇形
O
弧
A
半径
半径
B
图上A、B两点之间的部分叫做弧,读作“弧AB”。
扇形
O
弧
A
半径
半径
B
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
扇形
O
弧
圆心角
A
半径
半径
B
顶点在圆心的角叫做圆心角。
一个公园是圆形布局,半径长1km,圆心处设立了一个纪念碑。公园共有四个门,每两个相邻的门之间有一条直的水泥路相通,长约1.41km。
(1)这个公园的围墙有多长?
C=2πr
= 6.28(km)
= 2×3.14×1
答:这个公园的围墙长6.28千米。
西门
南门
东门
小湖
纪念碑
北门
随堂练习
(教科书113页第4题)
= 2(km)
1+1
答:北门在南门的正北方向,
距离南门有2千米。
西门
南门
东门
小湖
纪念碑
北门
(2)北门在南门的什么方向?距离南门多远?
西门
南门
东门
小湖
纪念碑
北门
(3)如果公园里有一个半径为0.2km的圆形小湖,
这个公园的陆地面积是多少平方千米?
3.14×12?3.14×0.22
= 3.0144(km2)
答:这个公园的陆地面积
是3.0144平方千米。
西门
南门
东门
小湖
纪念碑
北门
(4)请你再提出一些数学问题并试着解决。
2?1.41=0.59(千米)
答:东门到西门的距离比东门
到南门远0.59千米。
答案不唯一。
如:东门到西门的距离比东门到
南门远多少千米?
综合运用
1.填空题。
一个圆的直径是2m,它的周长是( ) m,面积是( ) m2。
已知圆的周长,求d=( ),求r=( )。
圆的半径扩大3倍,直径就扩大( )倍,周长就扩大( )倍,面积就扩大( )倍。
6.28
3.14
3
3
9
7000÷(3.14×0.6×120)
≈31(分钟)
答:他经过这个大桥大约要31分钟。
一辆自行车的外轮直径是0.6m,如果小明骑车平均每分钟转120圈,他经过7000m的大桥要几分钟?(得数保留整数)
2.
=1.2(m)
4.8÷4
正方形边长:
剪下来的面积:
1.2×1.2?3.14×(1.2÷2)2
= 1.22?3.14×0.62
= 1.44?1.1304
= 0.3096(平方米)
答:剪下来的纸的面积是0.3096平方米。
在一个周长为4.8m的正方形纸片内,要剪一个最大的圆,剪下来的纸的面积是多少平方米?
3.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
