五年级上册数学课件-第八单元第3课时 多边形的面积 人教版(共20张PPT)
文档属性
| 名称 | 五年级上册数学课件-第八单元第3课时 多边形的面积 人教版(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-20 21:24:28 | ||
图片预览




文档简介
总复习
8
人教版五年级数学上册
第3课时 多边形的面积
一 整体回顾
想一想,关于多边形的面积你学到了哪些知识?
平行四边的面积
梯形的面积
组合图形的面积
三角形的面积
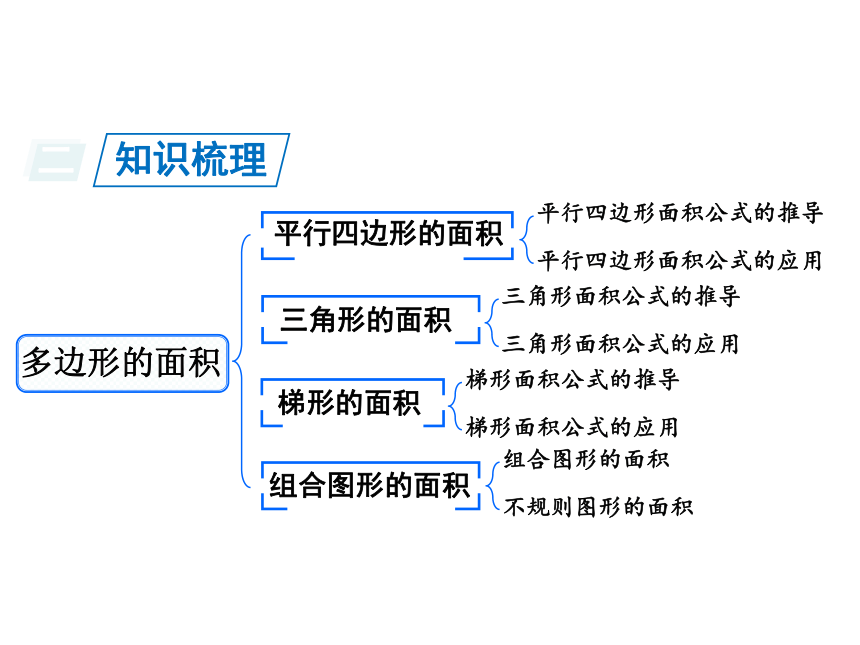
二 知识梳理
多边形的面积
多边形的面积公式
图形
面积公式
长方形
正方形
平行四边形
三角形
梯形
S=ab
S=(a+b)h÷2
S=a2
S=ah
S=ah÷2
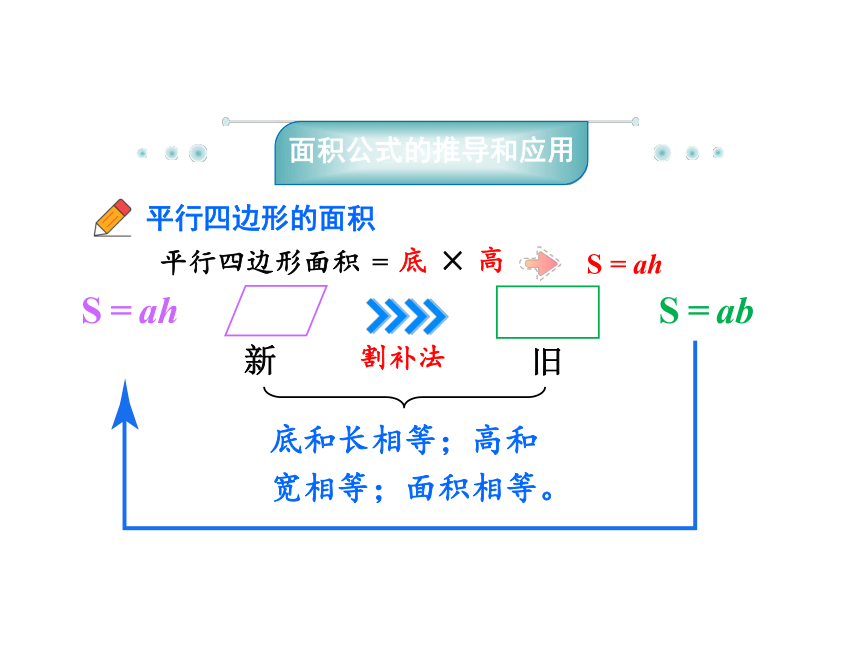
面积公式的推导和应用
平行四边形的面积
S=ah
平行四边形面积
底
高
×
=
新
旧
割补法
底和长相等;高和宽相等;面积相等。
S=ab
S=ah
平行四边形面积公式的应用
在平行四边形中,只要知道底、高和面积三个量中的任意两个量,就可以根据平行四边形的面积计算公式求出第三个量。
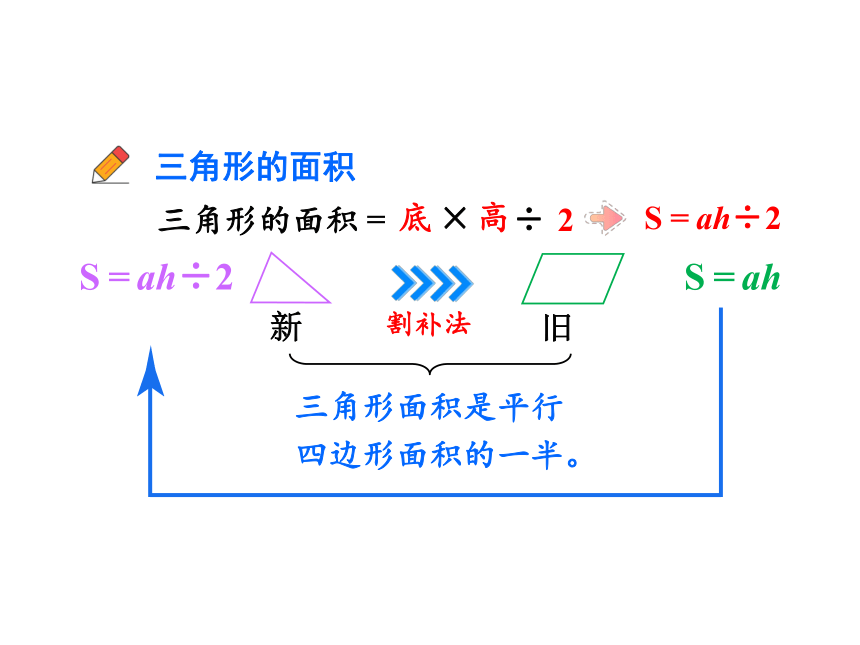
三角形的面积
三角形的面积
底
高
×
=
÷
2
S=ah÷2
割补法
三角形面积是平行四边形面积的一半。
S=ah
S=ah÷2
旧
新
三角形面积公式的应用
在三角形中,只要知道三角形的底、高和面积这三个量中的任意两个量,就可以根据三角形的面积计算公式求出第三个量。
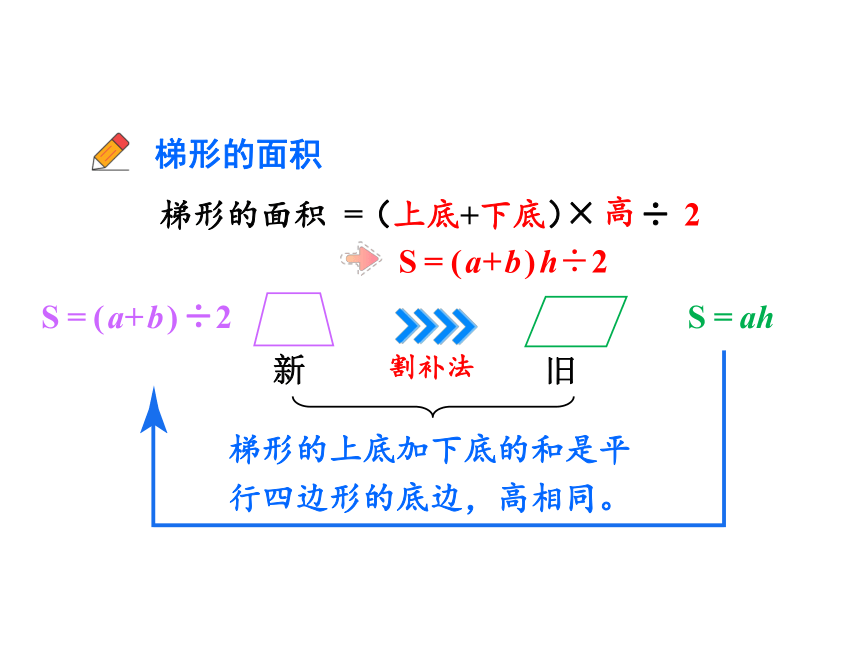
梯形的面积
割补法
梯形的上底加下底的和是平行四边形的底边,高相同。
S=ah
S=(a+b)÷2
旧
新
(上底+下底)
梯形的面积
高
×
=
÷
2
S=(a+b)h÷2
梯形面积公式的应用
如果知道梯形的面积、上底、下底和高这四个量中的任意三个量,就可以根据梯形的面积计算公式求出第四个量。
在实际生活中,有些图形是由几个简单的图形组合而成的。在计算组合图形的面积时,通常有两种方法:分割求和法和添补求差法。
分割求和法
先把图形分解成几个学习过的简单图形,分别计算出各个简单图形的面积,然后加起来,即可求出整个图形的面积。
组合图形的面积
在实际生活中,有些图形是由几个简单的图形组合而成的。在计算组合图形的面积时,通常有两种方法:分割求和法和添补求差法。
添补求差法
有些组合图形时从已学过的简单图形中减去一个(或几个)已学过的简单图形而构成,需要从一个图形面积中减去另一个(或几个)图形的面积。
组合图形的面积
三 随堂练习
下面这块地种了三种蔬菜。茄子、西红柿和西瓜各种了多少平方米?这块地共有多少平方米?
1.
[教科书第113页3(1)]
S茄子=15×32÷2=240(m2)
S黄瓜=25×32=800(m2)
S西红柿=(15+23)×32÷2
=608 (m2)
S这块地=240+800+608
=1648(m2)
茄子种了240m2,黄瓜种了800m2,西红柿种了608m2,这块地共有1648m2。
答:
32m
一个直角三角形的三条边长分别是3cm、4cm、5cm。以这三条边分别为边长画三个正方形,这三个正方形的面积各是多少?
2.
(教科书第114页思考题)
S=a2
S红=32=9(cm2)
S绿=42=16(cm2)
S黄=52=25(cm2)
9+16=25,两个小正方形的面积的和等于大正方形的面积。
如果直角三角形三条边的边长分别是6cm、8cm、10cm或5cm、12cm、13cm呢?
S红=62=36(cm2)
S绿=82=64(cm2)
S黄=102=100(cm2)
S红=52=25(cm2)
S绿=122=144(cm2)
S黄=132=169(cm2)
两个小正方形的面积的和等于大正方形的面积。
四 综合运用
填空题。
1.
在一个面积是50.4cm2的长方形内画一个最大的三角形,这个三角形的面积是( )cm2 。
25.2
一个直角梯形的上底是8cm,如果把下底减少3cm,这个梯形就变成了正方形,原梯形的面积是( ) cm2 。
76
求组合图形的面积。(单位:cm)
2.
S=8×6?4×3
=48?12
=36(cm2)
S= 20×10?(6+10)×(20?12)÷2
= 200?64
= 136(cm2)
8
6
4
3
20
12
6
10
解决问题。
3.
王叔叔要粉刷一面墙(如图),如果每平方米用水泥3.5kg,粉装这面墙至少需要水泥多少千克?
解:
这边墙的面积是:
3.5×34=119(kg)
答:
粉装这面墙至少需要水泥119kg。
S= 8×3+8×2.5÷2
= 24+10
= 34(m2)
8m
3m
2.5m
估计下面图形的面积。(每个小方格的面积是1cm2)
S大长方形=8×6=48(cm2)
8
6
4
1
S小长方形=4×1=4(cm2)
S不规则图形=48+4=52(cm2)
答:
不规则图形的面积大约是52cm2。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
8
人教版五年级数学上册
第3课时 多边形的面积
一 整体回顾
想一想,关于多边形的面积你学到了哪些知识?
平行四边的面积
梯形的面积
组合图形的面积
三角形的面积
二 知识梳理
多边形的面积
多边形的面积公式
图形
面积公式
长方形
正方形
平行四边形
三角形
梯形
S=ab
S=(a+b)h÷2
S=a2
S=ah
S=ah÷2
面积公式的推导和应用
平行四边形的面积
S=ah
平行四边形面积
底
高
×
=
新
旧
割补法
底和长相等;高和宽相等;面积相等。
S=ab
S=ah
平行四边形面积公式的应用
在平行四边形中,只要知道底、高和面积三个量中的任意两个量,就可以根据平行四边形的面积计算公式求出第三个量。
三角形的面积
三角形的面积
底
高
×
=
÷
2
S=ah÷2
割补法
三角形面积是平行四边形面积的一半。
S=ah
S=ah÷2
旧
新
三角形面积公式的应用
在三角形中,只要知道三角形的底、高和面积这三个量中的任意两个量,就可以根据三角形的面积计算公式求出第三个量。
梯形的面积
割补法
梯形的上底加下底的和是平行四边形的底边,高相同。
S=ah
S=(a+b)÷2
旧
新
(上底+下底)
梯形的面积
高
×
=
÷
2
S=(a+b)h÷2
梯形面积公式的应用
如果知道梯形的面积、上底、下底和高这四个量中的任意三个量,就可以根据梯形的面积计算公式求出第四个量。
在实际生活中,有些图形是由几个简单的图形组合而成的。在计算组合图形的面积时,通常有两种方法:分割求和法和添补求差法。
分割求和法
先把图形分解成几个学习过的简单图形,分别计算出各个简单图形的面积,然后加起来,即可求出整个图形的面积。
组合图形的面积
在实际生活中,有些图形是由几个简单的图形组合而成的。在计算组合图形的面积时,通常有两种方法:分割求和法和添补求差法。
添补求差法
有些组合图形时从已学过的简单图形中减去一个(或几个)已学过的简单图形而构成,需要从一个图形面积中减去另一个(或几个)图形的面积。
组合图形的面积
三 随堂练习
下面这块地种了三种蔬菜。茄子、西红柿和西瓜各种了多少平方米?这块地共有多少平方米?
1.
[教科书第113页3(1)]
S茄子=15×32÷2=240(m2)
S黄瓜=25×32=800(m2)
S西红柿=(15+23)×32÷2
=608 (m2)
S这块地=240+800+608
=1648(m2)
茄子种了240m2,黄瓜种了800m2,西红柿种了608m2,这块地共有1648m2。
答:
32m
一个直角三角形的三条边长分别是3cm、4cm、5cm。以这三条边分别为边长画三个正方形,这三个正方形的面积各是多少?
2.
(教科书第114页思考题)
S=a2
S红=32=9(cm2)
S绿=42=16(cm2)
S黄=52=25(cm2)
9+16=25,两个小正方形的面积的和等于大正方形的面积。
如果直角三角形三条边的边长分别是6cm、8cm、10cm或5cm、12cm、13cm呢?
S红=62=36(cm2)
S绿=82=64(cm2)
S黄=102=100(cm2)
S红=52=25(cm2)
S绿=122=144(cm2)
S黄=132=169(cm2)
两个小正方形的面积的和等于大正方形的面积。
四 综合运用
填空题。
1.
在一个面积是50.4cm2的长方形内画一个最大的三角形,这个三角形的面积是( )cm2 。
25.2
一个直角梯形的上底是8cm,如果把下底减少3cm,这个梯形就变成了正方形,原梯形的面积是( ) cm2 。
76
求组合图形的面积。(单位:cm)
2.
S=8×6?4×3
=48?12
=36(cm2)
S= 20×10?(6+10)×(20?12)÷2
= 200?64
= 136(cm2)
8
6
4
3
20
12
6
10
解决问题。
3.
王叔叔要粉刷一面墙(如图),如果每平方米用水泥3.5kg,粉装这面墙至少需要水泥多少千克?
解:
这边墙的面积是:
3.5×34=119(kg)
答:
粉装这面墙至少需要水泥119kg。
S= 8×3+8×2.5÷2
= 24+10
= 34(m2)
8m
3m
2.5m
估计下面图形的面积。(每个小方格的面积是1cm2)
S大长方形=8×6=48(cm2)
8
6
4
1
S小长方形=4×1=4(cm2)
S不规则图形=48+4=52(cm2)
答:
不规则图形的面积大约是52cm2。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
