第一章 反比例函数专项训练 反比例函数与一次函数、几何图形综合题(含答案)
文档属性
| 名称 | 第一章 反比例函数专项训练 反比例函数与一次函数、几何图形综合题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-21 07:21:59 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
专项训练 反比例函数与一次函数、几何图形综合题
一、反比例函数与一次函数综合题
1.(2018·广元)如图所示为一次函数y=ax-2a与反比例函数y=-(a≠0)在同一坐标系中的大致图象,其中较准确的是( )
2.(2019·日照)在同一平面直角坐标系中,函数y=kx+1(k≠0)和y=(k≠0)的图象大致是( )
3.(2018·铜仁)如图所示,已知一次函数y=ax+b和反比例函数y=的图象相交于A(-2,y1),B(1,y2)两点,则不等式ax+b<的解集为( )
A.x<-2或0<x<1 B.x<-2
C.0<x<1 D.-2<x<0或x>1
4.(2019·扬州)若反比例函数y=-的图象上有两个不同的点关于y轴的对称点都在一次函数
y=-x+m的图象上,则m的取值范围是( )
A.m>2 B.m<-2 C.m>2或m<-2 D.-2<m<2
5.(2019·凉山州)如图所示,正比例函数y=kx与反比例函数y=的图象相交于A,C 两点,过点A作x轴的垂线交x轴于点B,连接BC,则△ABC的面积等于( )
A. 8 B. 6 C. 4 D. 2
6.(2018·乐山)如图所示,曲线C2是双曲线C1:y=(x>0)绕原点O逆时针旋转45°得到的图形,P是曲线C2上任意一点,点A在直线:y=x上,且PA=PO,则△POA的面积等于( )
B. 6 C. 3 D. 12
7.(2019·玉林)如图所示,一次函数y1=(k-5)x+b的图象在第一象限与反比例函数y2=的图象相交于A,B两点,当y1>y2时,x的取值范围是1<x<4,则k=_____________。
8.(2018·赤峰)如图所示,已知一次函数y=-x+b与反比例函数
y=(k≠0)的图象相交于点P,则关于x的方程-x+b=的
解是_______________。
9.(2019·大庆)如图所示,反比例函数y=和一次函数y=kx-1的图象相交于A(m,2m),B两点。
(1)求一次函数的表达式;
(2)求出点B的坐标,并根据图象直接写出满足不等式<kx-1的x的取值范围。
二、反比例函数与几何图形综合题
10.(2018·长春)如图所示,在平面直角坐标系中,等腰直角三角形ABC的顶点A,B分别在x轴,y轴的正半轴上,∠ABC=90°,CA⊥x轴,点C在函数y=(x>0)的图象上,若AB=2,则k的值为( )
A. 4 B. 2 C. 2 D.
11.(2019·赤峰)如图所示,点P是反比例函数y=(k≠0)的图象上任意一点,过点P作PM⊥x轴,垂足为M.若△POM的面积等于2,则k的值等于( )
A. -4 B. 4 C. -2 D. 2
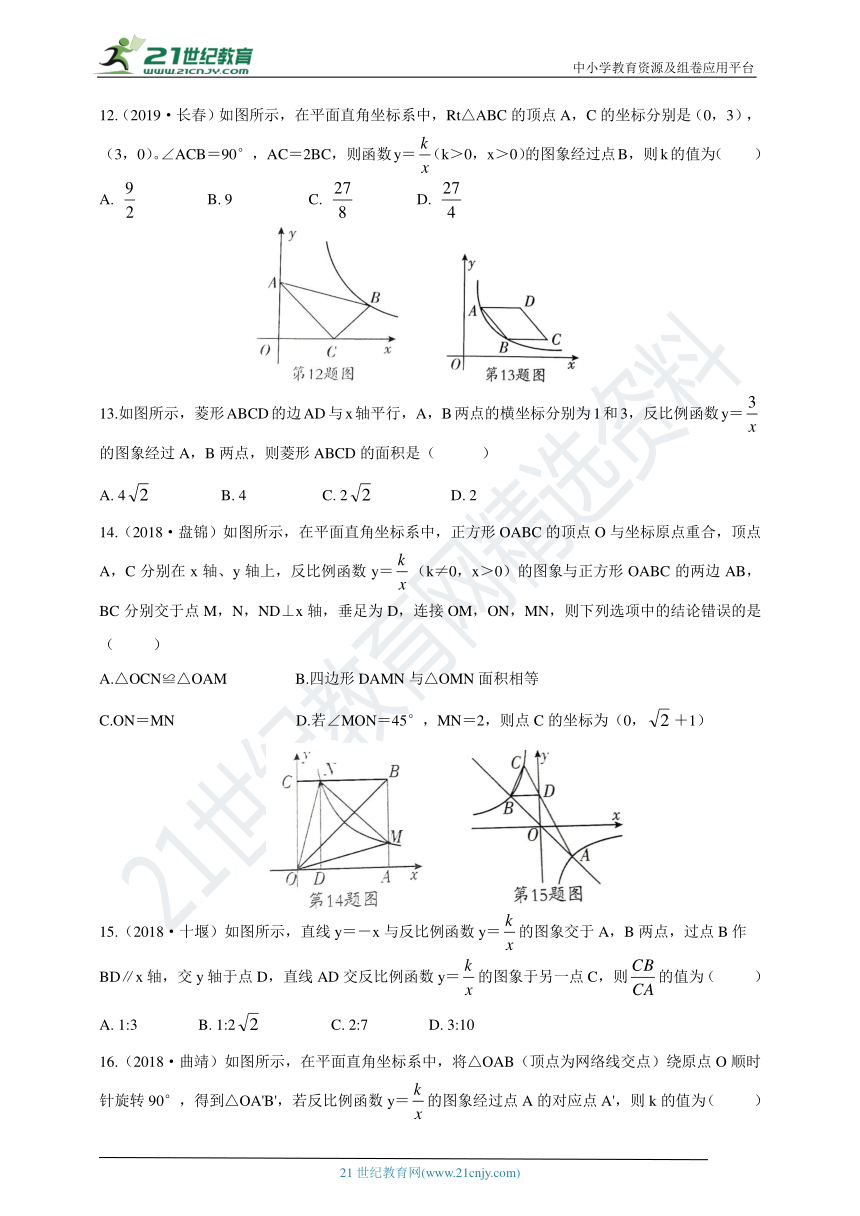
12.(2019·长春)如图所示,在平面直角坐标系中,Rt△ABC的顶点A,C的坐标分别是(0,3),(3,0)。∠ACB=90°,AC=2BC,则函数y=(k>0,x>0)的图象经过点B,则k的值为( )
A. B. 9 C. D.
13.如图所示,菱形ABCD的边AD与x轴平行,A,B两点的横坐标分别为1和3,反比例函数y=的图象经过A,B两点,则菱形ABCD的面积是( )
A. 4 B. 4 C. 2 D. 2
14.(2018·盘锦)如图所示,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,顶点A,C分别在x轴、y轴上,反比例函数y=(k≠0,x>0)的图象与正方形OABC的两边AB,BC分别交于点M,N,ND⊥x轴,垂足为D,连接OM,ON,MN,则下列选项中的结论错误的是( )
A.△OCN≌△OAM B.四边形DAMN与△OMN面积相等
C.ON=MN D.若∠MON=45°,MN=2,则点C的坐标为(0,+1)
15.(2018·十堰)如图所示,直线y=-x与反比例函数y=的图象交于A,B两点,过点B作
BD∥x轴,交y轴于点D,直线AD交反比例函数y=的图象于另一点C,则的值为( )
1:3 B. 1:2 C. 2:7 D. 3:10
16.(2018·曲靖)如图所示,在平面直角坐标系中,将△OAB(顶点为网络线交点)绕原点O顺时针旋转90°,得到△OA'B',若反比例函数y=的图象经过点A的对应点A',则k的值为( )
A. 6 B.-3 C. 3 D. -6
17.(2019·沈阳)如图所示,正比例函数y1=k1x的图象与反比例函数y2=(x>0)的图象相交于点A(,2),点B是反比例函数图象上一点,它的横坐标是3,连接OB,AB,则△AOB的面积是_____________。
18.(2019·陕西)如图所示,D是矩形AOBC的对称中心,A(0,4),B(6,0),若一个反比例函数的图象经过点D,交AC于点M,则点M的坐标为___________。
19.(2019·黄冈)如图所示,一直线经过原点O,且与反比例函数y=(k>0)相交于点A,点B,过点A作AC⊥y轴,垂足为C,连接BC.若△ABC面积为8,则k=____________。
20.(2018·宁夏)在平面直角坐标系中,四边形AOBC为矩形,且点C坐标为(8,6),M为BC中点,反比例函数y=(k是常数,k≠0)的图象经过点M,交AC于点N,则MN的长度是__________。
21.(2018·桂林)如图所示,矩形OABC的边AB与x轴交于点D,与反比例函数y=(k>0)在第一象限的图象交于点E,∠AOD=30°,点E的纵坐标为1,△ODE的面积是,则k的值是_____________。
22.(2019·鞍山)如图所示,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与y轴交于点C,与反比例函数y=(k≠0)的图象交于A,B两点,点A在第一象限,纵坐标为4,点B在第三象限,BM⊥x轴,垂足为点M,BM=OM=2.
(1)求反比例函数和一次函数的解析式;
(2)连接OB,MC,求四边形MBOC的面积.
23.(2019·盘锦)如图所示,四边形ABCD是矩形,点A在第四象限y1=的图象上,点B在第一象限y2=的图象上,AB交x轴于点E,点C与点D在y轴上,AD=,S矩形OCBE=S矩形ODAE。
(1)求点B的坐标;
(2)若点P在x轴上,S△BPE=3,求直线BP的解析式。
参考答案
一、反比例函数与一次函数综合题
1. B 2. C 3. D 4. C 5. C 6. B
7. 4 8. x1=1,x2=2
9. 解:(1)∵A(m,2m)在反比例函数图象上,∴2m=.∴m=1.∴A(1,2).
又∵A(1,2)在一次函数y=kx-1的图象上,∴2=k-1,即k=3.
∴一次函数的表达式为y=3x-1;
(2)由’解得或。∴B(-,-3).
∴不等式<kx-1的x的取值范围为-<x<0或x>1.
二、反比例函数与几何图形综合题
10. A 11. A 12. D 13. A 14. C 15. A 16. C
17. 2 18. (,4) 19. 8 20. 5 21. 3
22.解:(1)∵BM=OM=2,∴点B的坐标为(-2,-2).
∵反比例函数y=(k≠0)的图象经过点B,则-2=,得k=4.
∴反比例函数的解析式为y=。∵点A的纵坐标是4,∴4=,得x=1.
∴点A的坐标为(1,4).
∵一次函数y=mx+n(m≠0)的图象过点A(1,4)、点B(-2,-2),
∴,解得,∴一次函数的解析式为y=2x+2;
(2)∵y=2x+2与y轴交于点C,∴点C的坐标为(0,2).
∵点B(-2,-2),点M(-2,0),∴OC=MB=2.∵ BM⊥x轴,∴MB//OC.
∴四边形MBOC是平行四边形。∴四边形MBOC的面积为OM·OC=4。
23,解:(1)∵S矩形OCBE=S矩形ODAE,点B在第一象限y2=的图象上,点A在第四象限y1=-的图象上,∴S矩形ODAE=2.∴S矩形OCBE=×2=3.∴k=3。∴y2=。
∵OE=AD=,∴B的横坐标为,代入y2=得,y=2.∴点B的坐标为(,2);
(2)设P(a,0),
∵S△BPE=PE·BE==3,解得a=-或.
∴点P的坐标为(-,0)或(,0).
设直线BP的解析式为y=mx+n(m≠0),
①若直线过(,2),(-,0),
则,解得。∴直线BP的解析式为y=x+1;
②若直线过(,2)(,0),
则,解得,∴直线BP的解析式为y=-x+3。
综上所述,直线BP的解析式是y=x+1或y=-x+3.
_21?????????è?????(www.21cnjy.com)_
专项训练 反比例函数与一次函数、几何图形综合题
一、反比例函数与一次函数综合题
1.(2018·广元)如图所示为一次函数y=ax-2a与反比例函数y=-(a≠0)在同一坐标系中的大致图象,其中较准确的是( )
2.(2019·日照)在同一平面直角坐标系中,函数y=kx+1(k≠0)和y=(k≠0)的图象大致是( )
3.(2018·铜仁)如图所示,已知一次函数y=ax+b和反比例函数y=的图象相交于A(-2,y1),B(1,y2)两点,则不等式ax+b<的解集为( )
A.x<-2或0<x<1 B.x<-2
C.0<x<1 D.-2<x<0或x>1
4.(2019·扬州)若反比例函数y=-的图象上有两个不同的点关于y轴的对称点都在一次函数
y=-x+m的图象上,则m的取值范围是( )
A.m>2 B.m<-2 C.m>2或m<-2 D.-2<m<2
5.(2019·凉山州)如图所示,正比例函数y=kx与反比例函数y=的图象相交于A,C 两点,过点A作x轴的垂线交x轴于点B,连接BC,则△ABC的面积等于( )
A. 8 B. 6 C. 4 D. 2
6.(2018·乐山)如图所示,曲线C2是双曲线C1:y=(x>0)绕原点O逆时针旋转45°得到的图形,P是曲线C2上任意一点,点A在直线:y=x上,且PA=PO,则△POA的面积等于( )
B. 6 C. 3 D. 12
7.(2019·玉林)如图所示,一次函数y1=(k-5)x+b的图象在第一象限与反比例函数y2=的图象相交于A,B两点,当y1>y2时,x的取值范围是1<x<4,则k=_____________。
8.(2018·赤峰)如图所示,已知一次函数y=-x+b与反比例函数
y=(k≠0)的图象相交于点P,则关于x的方程-x+b=的
解是_______________。
9.(2019·大庆)如图所示,反比例函数y=和一次函数y=kx-1的图象相交于A(m,2m),B两点。
(1)求一次函数的表达式;
(2)求出点B的坐标,并根据图象直接写出满足不等式<kx-1的x的取值范围。
二、反比例函数与几何图形综合题
10.(2018·长春)如图所示,在平面直角坐标系中,等腰直角三角形ABC的顶点A,B分别在x轴,y轴的正半轴上,∠ABC=90°,CA⊥x轴,点C在函数y=(x>0)的图象上,若AB=2,则k的值为( )
A. 4 B. 2 C. 2 D.
11.(2019·赤峰)如图所示,点P是反比例函数y=(k≠0)的图象上任意一点,过点P作PM⊥x轴,垂足为M.若△POM的面积等于2,则k的值等于( )
A. -4 B. 4 C. -2 D. 2
12.(2019·长春)如图所示,在平面直角坐标系中,Rt△ABC的顶点A,C的坐标分别是(0,3),(3,0)。∠ACB=90°,AC=2BC,则函数y=(k>0,x>0)的图象经过点B,则k的值为( )
A. B. 9 C. D.
13.如图所示,菱形ABCD的边AD与x轴平行,A,B两点的横坐标分别为1和3,反比例函数y=的图象经过A,B两点,则菱形ABCD的面积是( )
A. 4 B. 4 C. 2 D. 2
14.(2018·盘锦)如图所示,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,顶点A,C分别在x轴、y轴上,反比例函数y=(k≠0,x>0)的图象与正方形OABC的两边AB,BC分别交于点M,N,ND⊥x轴,垂足为D,连接OM,ON,MN,则下列选项中的结论错误的是( )
A.△OCN≌△OAM B.四边形DAMN与△OMN面积相等
C.ON=MN D.若∠MON=45°,MN=2,则点C的坐标为(0,+1)
15.(2018·十堰)如图所示,直线y=-x与反比例函数y=的图象交于A,B两点,过点B作
BD∥x轴,交y轴于点D,直线AD交反比例函数y=的图象于另一点C,则的值为( )
1:3 B. 1:2 C. 2:7 D. 3:10
16.(2018·曲靖)如图所示,在平面直角坐标系中,将△OAB(顶点为网络线交点)绕原点O顺时针旋转90°,得到△OA'B',若反比例函数y=的图象经过点A的对应点A',则k的值为( )
A. 6 B.-3 C. 3 D. -6
17.(2019·沈阳)如图所示,正比例函数y1=k1x的图象与反比例函数y2=(x>0)的图象相交于点A(,2),点B是反比例函数图象上一点,它的横坐标是3,连接OB,AB,则△AOB的面积是_____________。
18.(2019·陕西)如图所示,D是矩形AOBC的对称中心,A(0,4),B(6,0),若一个反比例函数的图象经过点D,交AC于点M,则点M的坐标为___________。
19.(2019·黄冈)如图所示,一直线经过原点O,且与反比例函数y=(k>0)相交于点A,点B,过点A作AC⊥y轴,垂足为C,连接BC.若△ABC面积为8,则k=____________。
20.(2018·宁夏)在平面直角坐标系中,四边形AOBC为矩形,且点C坐标为(8,6),M为BC中点,反比例函数y=(k是常数,k≠0)的图象经过点M,交AC于点N,则MN的长度是__________。
21.(2018·桂林)如图所示,矩形OABC的边AB与x轴交于点D,与反比例函数y=(k>0)在第一象限的图象交于点E,∠AOD=30°,点E的纵坐标为1,△ODE的面积是,则k的值是_____________。
22.(2019·鞍山)如图所示,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与y轴交于点C,与反比例函数y=(k≠0)的图象交于A,B两点,点A在第一象限,纵坐标为4,点B在第三象限,BM⊥x轴,垂足为点M,BM=OM=2.
(1)求反比例函数和一次函数的解析式;
(2)连接OB,MC,求四边形MBOC的面积.
23.(2019·盘锦)如图所示,四边形ABCD是矩形,点A在第四象限y1=的图象上,点B在第一象限y2=的图象上,AB交x轴于点E,点C与点D在y轴上,AD=,S矩形OCBE=S矩形ODAE。
(1)求点B的坐标;
(2)若点P在x轴上,S△BPE=3,求直线BP的解析式。
参考答案
一、反比例函数与一次函数综合题
1. B 2. C 3. D 4. C 5. C 6. B
7. 4 8. x1=1,x2=2
9. 解:(1)∵A(m,2m)在反比例函数图象上,∴2m=.∴m=1.∴A(1,2).
又∵A(1,2)在一次函数y=kx-1的图象上,∴2=k-1,即k=3.
∴一次函数的表达式为y=3x-1;
(2)由’解得或。∴B(-,-3).
∴不等式<kx-1的x的取值范围为-<x<0或x>1.
二、反比例函数与几何图形综合题
10. A 11. A 12. D 13. A 14. C 15. A 16. C
17. 2 18. (,4) 19. 8 20. 5 21. 3
22.解:(1)∵BM=OM=2,∴点B的坐标为(-2,-2).
∵反比例函数y=(k≠0)的图象经过点B,则-2=,得k=4.
∴反比例函数的解析式为y=。∵点A的纵坐标是4,∴4=,得x=1.
∴点A的坐标为(1,4).
∵一次函数y=mx+n(m≠0)的图象过点A(1,4)、点B(-2,-2),
∴,解得,∴一次函数的解析式为y=2x+2;
(2)∵y=2x+2与y轴交于点C,∴点C的坐标为(0,2).
∵点B(-2,-2),点M(-2,0),∴OC=MB=2.∵ BM⊥x轴,∴MB//OC.
∴四边形MBOC是平行四边形。∴四边形MBOC的面积为OM·OC=4。
23,解:(1)∵S矩形OCBE=S矩形ODAE,点B在第一象限y2=的图象上,点A在第四象限y1=-的图象上,∴S矩形ODAE=2.∴S矩形OCBE=×2=3.∴k=3。∴y2=。
∵OE=AD=,∴B的横坐标为,代入y2=得,y=2.∴点B的坐标为(,2);
(2)设P(a,0),
∵S△BPE=PE·BE==3,解得a=-或.
∴点P的坐标为(-,0)或(,0).
设直线BP的解析式为y=mx+n(m≠0),
①若直线过(,2),(-,0),
则,解得。∴直线BP的解析式为y=x+1;
②若直线过(,2)(,0),
则,解得,∴直线BP的解析式为y=-x+3。
综上所述,直线BP的解析式是y=x+1或y=-x+3.
_21?????????è?????(www.21cnjy.com)_
