2.1.2 空间中直线与直线之间的位置关系(22张PPT)
文档属性
| 名称 | 2.1.2 空间中直线与直线之间的位置关系(22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 610.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-21 20:21:53 | ||
图片预览




文档简介
(共22张PPT)
2.1.2空间中直线与直线之间的位置关系
观察下面的图片,图片中的直线有几
种位置关系?
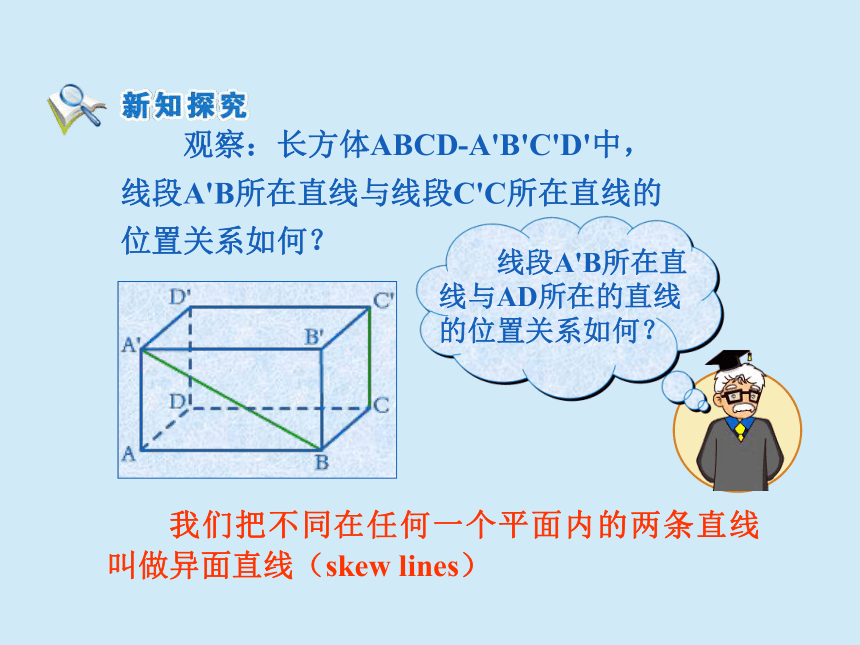
我们把不同在任何一个平面内的两条直线叫做异面直线(skew
lines)
观察:长方体ABCD-A'B'C'D'中,
线段A'B所在直线与线段C'C所在直线的
位置关系如何?
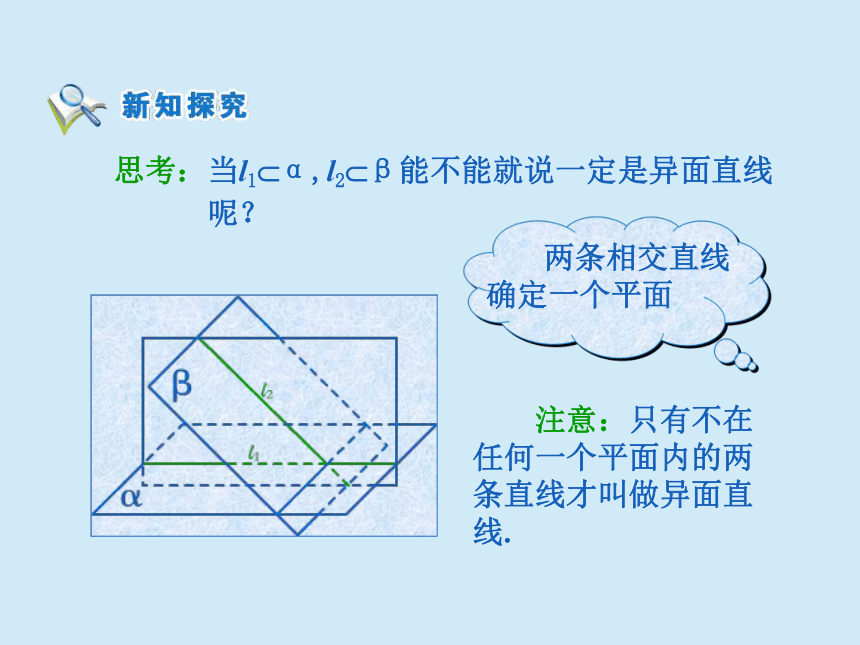
思考:当l1?α,l2?β能不能就说一定是异面直线
呢?
注意:只有不在任何一个平面内的两条直线才叫做异面直线.
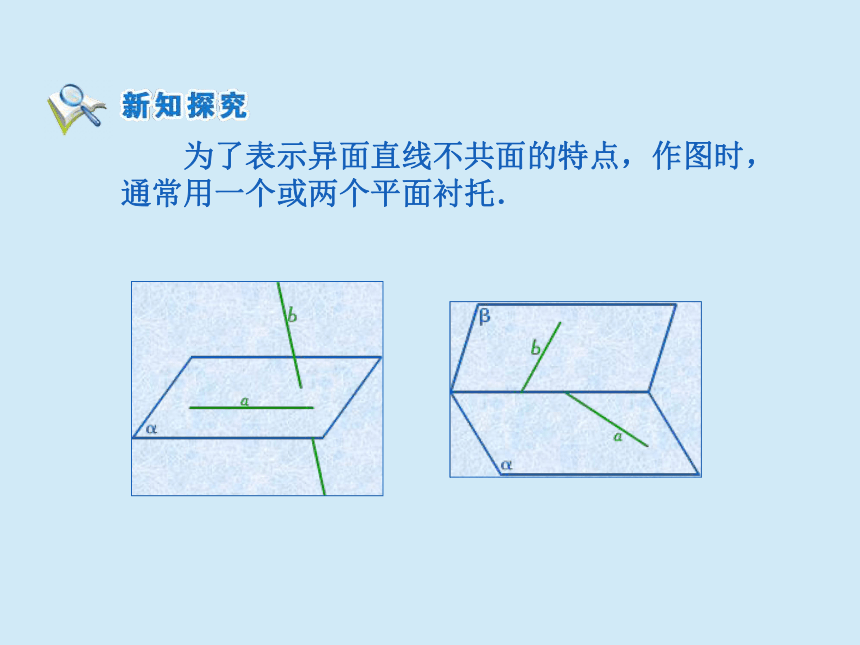
为了表示异面直线不共面的特点,作图时,
通常用一个或两个平面衬托.
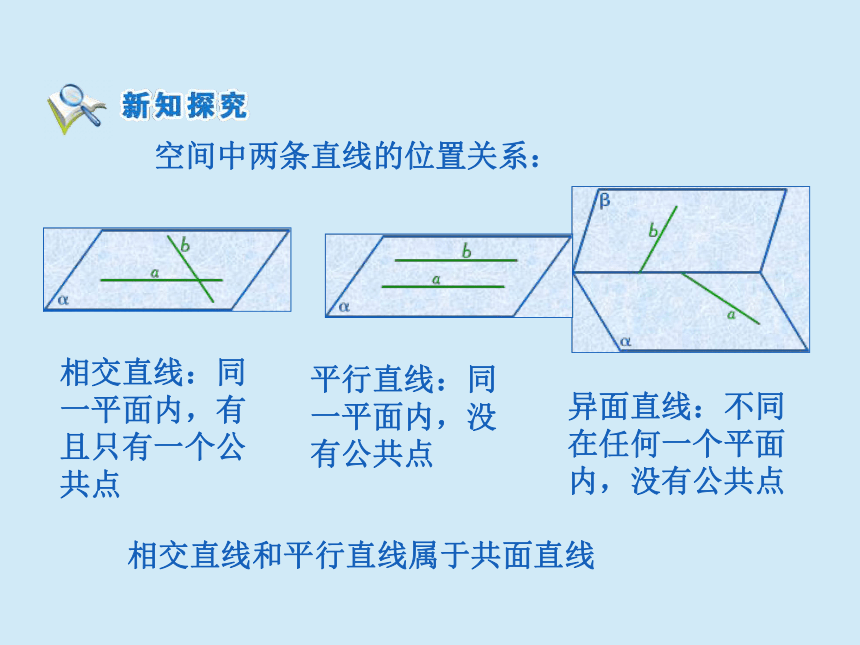
空间中两条直线的位置关系:
异面直线:不同
在任何一个平面
内,没有公共点
相交直线:同
一平面内,有
且只有一个公
共点
平行直线:同
一平面内,没
有公共点
相交直线和平行直线属于共面直线
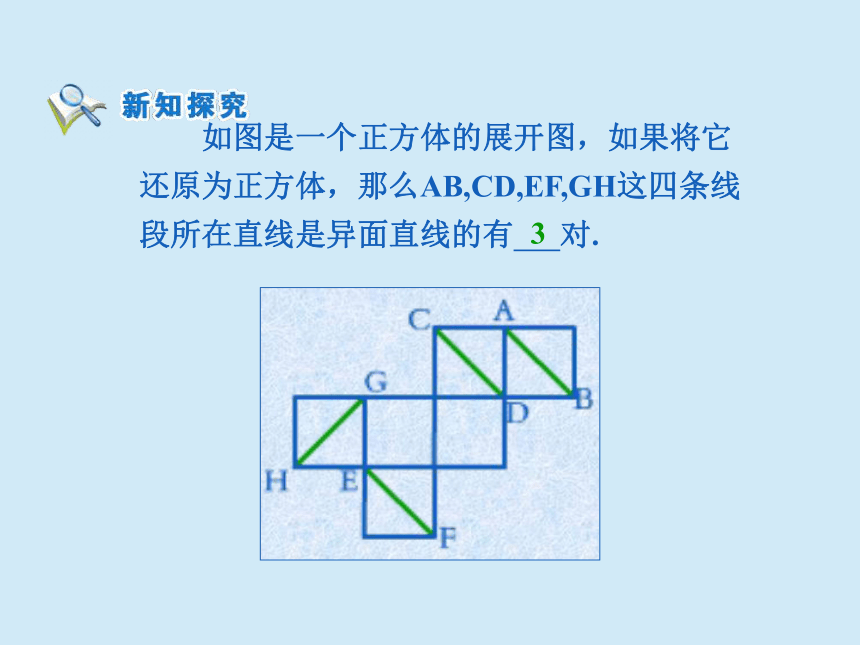
如图是一个正方体的展开图,如果将它
还原为正方体,那么AB,CD,EF,GH这四条线
段所在直线是异面直线的有
对.
3
观察:如图,长方体ABCD-A'B'C'D'
中,BB'∥AA',DD'∥AA',那么BB'与DD'平行
吗?
公理4:(也叫平行线的传递性)
平行于同一条直线的两条直线互相平行.
如图:空间四边形ABCD中,E,F,G,H分别是
AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
证明:连接BD
因为EH是△ABD的中位线
所以EH∥BD,
同理,
因为EH∥FG,
所以四边形EFGH是平行四边形.
且EH=
且FG=
FG∥BD,
且EH=FG
如图:空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
思考:在平面上,我们容易证明“如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补”.空间中,结论是否仍然成立?
定理:空间中如果两个角的两边分别对应平
行,那么这两个角相等或互补
异面直线所成的角:是指这两条直线经过平移后处于相交位置时所成的锐角或直角.
思考:a'与b'所成角的大小与点O的位置有关吗?
如果两条异面直线所成的角是直角,那么我们就说这两条直线互相垂直.
两条互相垂直的异面直线a,b,记作:a⊥b
异面直线a,b所成的角是直角,记作:a⊥b
观察长方体ABCD-A'B'C'D',有没有两条棱所在的直线是互相垂直的异面直线?
如果两条平行直线中的一条与某一条直线垂直,那么,另一条直线是否也与这条直线垂直?
垂直于同一条直线的两条直线是否平行?
垂直于同一条直线的两条直线不一定平行
有
是
如图:已知正方体ABCD-A'B'C'D'
(1)哪些棱所在直线与直线BA'是异面直线?
(2)直线BA'和CC'的夹角是多少?
(3)哪些棱所在的直线与直线AA'垂直?
解:(1)棱AD,DC,CC',
DD',D'C',B'C'
所在直线与直线BA'
是异面直线.
如图:已知正方体ABCD-A'B'C'D'
(1)哪些棱所在直线与直线BA'是异面直线?
(2)直线BA'和CC'的夹角是多少?
(3)哪些棱所在的直线与直线AA'垂直?
解:(2)由BB'∥CC'可知,
∠B'BA'为异面直线
BA'与CC'的夹角,
∠B'BA'=45°,
所以直线BA'与CC'的
夹角为45°.
如图:已知正方体ABCD-A'B'C'D'
(1)哪些棱所在直线与直线BA'是异面直线?
(2)直线BA'和CC'的夹角是多少?
(3)哪些棱所在的直线与直线AA'垂直?
解:(3)直线AB,BC,CD,DA,
A'B',B'C',C'D',
D'A',分别与直线AA'
垂直.
(1)如图:AA'是长方体的一条棱,长
方体中与AA'平行的棱共有
条.
3
(2)如果OA∥O'A',OB∥O'B',那么∠AOB和∠A'O'B
.
相等或互补
(1)分别在两个平面内的两条直线间的位置关
系是(
)
A:异面
B:平行
C:相交
D:以上都有可能(2)把两条异面直线称作“一对”,在正方
体的
十二条棱中,异面直线的对数为(
)
A:12
B:24
C:36
D:48
D
B
已知长方体ABCD-A'B'C'D'中,AB=2
3,
AD=2
3,AA'=2.
(1)BC和A'C'所成的角是多少度?
(2)AA'和BC'所成的角是多少度?
解:(1)连接A'C',
所以∠B'C'A'是异面直线
A'C'与BC所成的角.
在直角三角形A'B'C'中,
所以∠B'C'A'=
因此,异面直线BC和A'C'所
成的角是45°.
因为BC∥B'C',
45°
解:(2)
连接BC',
所以∠B'BC'是异面直线AA'
与BC'所成的角.
在直角三角形B'BC'中,
所以BC'=
因此,异面直线AA'和BC'所成
的角是60°
因为AA'∥BB',
B`C`=
BB'=
AD=
AA'=
2,
4,
∠B'BC'=
60°
已知长方体ABCD-A'B'C'D'中,AB=2
3,
AD=2
3,AA'=2.
(1)BC和A'C'所成的角是多少度?
(2)AA'和BC'所成的角是多少度?
设异面直线a与b所成的角为50°,O为空间一定点,试讨论,过点O与a、b所成的角都是θ(0°≤θ≤90°)的直线
l
有且仅有几条?
2.1.2空间中直线与直线之间的位置关系
观察下面的图片,图片中的直线有几
种位置关系?
我们把不同在任何一个平面内的两条直线叫做异面直线(skew
lines)
观察:长方体ABCD-A'B'C'D'中,
线段A'B所在直线与线段C'C所在直线的
位置关系如何?
思考:当l1?α,l2?β能不能就说一定是异面直线
呢?
注意:只有不在任何一个平面内的两条直线才叫做异面直线.
为了表示异面直线不共面的特点,作图时,
通常用一个或两个平面衬托.
空间中两条直线的位置关系:
异面直线:不同
在任何一个平面
内,没有公共点
相交直线:同
一平面内,有
且只有一个公
共点
平行直线:同
一平面内,没
有公共点
相交直线和平行直线属于共面直线
如图是一个正方体的展开图,如果将它
还原为正方体,那么AB,CD,EF,GH这四条线
段所在直线是异面直线的有
对.
3
观察:如图,长方体ABCD-A'B'C'D'
中,BB'∥AA',DD'∥AA',那么BB'与DD'平行
吗?
公理4:(也叫平行线的传递性)
平行于同一条直线的两条直线互相平行.
如图:空间四边形ABCD中,E,F,G,H分别是
AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
证明:连接BD
因为EH是△ABD的中位线
所以EH∥BD,
同理,
因为EH∥FG,
所以四边形EFGH是平行四边形.
且EH=
且FG=
FG∥BD,
且EH=FG
如图:空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
思考:在平面上,我们容易证明“如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补”.空间中,结论是否仍然成立?
定理:空间中如果两个角的两边分别对应平
行,那么这两个角相等或互补
异面直线所成的角:是指这两条直线经过平移后处于相交位置时所成的锐角或直角.
思考:a'与b'所成角的大小与点O的位置有关吗?
如果两条异面直线所成的角是直角,那么我们就说这两条直线互相垂直.
两条互相垂直的异面直线a,b,记作:a⊥b
异面直线a,b所成的角是直角,记作:a⊥b
观察长方体ABCD-A'B'C'D',有没有两条棱所在的直线是互相垂直的异面直线?
如果两条平行直线中的一条与某一条直线垂直,那么,另一条直线是否也与这条直线垂直?
垂直于同一条直线的两条直线是否平行?
垂直于同一条直线的两条直线不一定平行
有
是
如图:已知正方体ABCD-A'B'C'D'
(1)哪些棱所在直线与直线BA'是异面直线?
(2)直线BA'和CC'的夹角是多少?
(3)哪些棱所在的直线与直线AA'垂直?
解:(1)棱AD,DC,CC',
DD',D'C',B'C'
所在直线与直线BA'
是异面直线.
如图:已知正方体ABCD-A'B'C'D'
(1)哪些棱所在直线与直线BA'是异面直线?
(2)直线BA'和CC'的夹角是多少?
(3)哪些棱所在的直线与直线AA'垂直?
解:(2)由BB'∥CC'可知,
∠B'BA'为异面直线
BA'与CC'的夹角,
∠B'BA'=45°,
所以直线BA'与CC'的
夹角为45°.
如图:已知正方体ABCD-A'B'C'D'
(1)哪些棱所在直线与直线BA'是异面直线?
(2)直线BA'和CC'的夹角是多少?
(3)哪些棱所在的直线与直线AA'垂直?
解:(3)直线AB,BC,CD,DA,
A'B',B'C',C'D',
D'A',分别与直线AA'
垂直.
(1)如图:AA'是长方体的一条棱,长
方体中与AA'平行的棱共有
条.
3
(2)如果OA∥O'A',OB∥O'B',那么∠AOB和∠A'O'B
.
相等或互补
(1)分别在两个平面内的两条直线间的位置关
系是(
)
A:异面
B:平行
C:相交
D:以上都有可能(2)把两条异面直线称作“一对”,在正方
体的
十二条棱中,异面直线的对数为(
)
A:12
B:24
C:36
D:48
D
B
已知长方体ABCD-A'B'C'D'中,AB=2
3,
AD=2
3,AA'=2.
(1)BC和A'C'所成的角是多少度?
(2)AA'和BC'所成的角是多少度?
解:(1)连接A'C',
所以∠B'C'A'是异面直线
A'C'与BC所成的角.
在直角三角形A'B'C'中,
所以∠B'C'A'=
因此,异面直线BC和A'C'所
成的角是45°.
因为BC∥B'C',
45°
解:(2)
连接BC',
所以∠B'BC'是异面直线AA'
与BC'所成的角.
在直角三角形B'BC'中,
所以BC'=
因此,异面直线AA'和BC'所成
的角是60°
因为AA'∥BB',
B`C`=
BB'=
AD=
AA'=
2,
4,
∠B'BC'=
60°
已知长方体ABCD-A'B'C'D'中,AB=2
3,
AD=2
3,AA'=2.
(1)BC和A'C'所成的角是多少度?
(2)AA'和BC'所成的角是多少度?
设异面直线a与b所成的角为50°,O为空间一定点,试讨论,过点O与a、b所成的角都是θ(0°≤θ≤90°)的直线
l
有且仅有几条?
