2019-2020学年黑龙江省绥化市绥棱县八年级下学期期末数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2019-2020学年黑龙江省绥化市绥棱县八年级下学期期末数学试卷(五四学制)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 874.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-21 06:56:28 | ||
图片预览



文档简介
2019-2020学年八年级第二学期期末数学试卷(五四学制)
一、选择题(共10小题).
1.函数y=的自变量x的取值范围是( )
A.x>2 B.x≥2 C.x≠2 D.x≤2
2.下列各式中,一定是二次根式的是( )
A. B. C. D.
3.矩形、菱形、正方形都具有的性质是( )
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.对角线平分对角
4.下列各组长度的线段中,可以组成直角三角形的是( )
A.1,2,3 B.3,4,5 C.1,,3 D.5,6,7
5.顺次连接矩形的四边形中点所得的四边形一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
6.函数y=3x﹣5的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.数据:a,1,2,3,6的平均数为3,则这组数据的众数是( )
A.2 B.0 C.4 D.3
8.一个正比例函数的图象经过点(﹣2,4),它的表达式为( )
A.y=﹣2x B.y=2x C.y=﹣x D.y=x
9.一次函数y1=kx+b与y2=x+a的图象如下图所示,则下列结论:①k<0;②a>0;③b>0;④当x<3时y1<y2.其中正确的个数( )
A.0 B.1 C.2 D.3
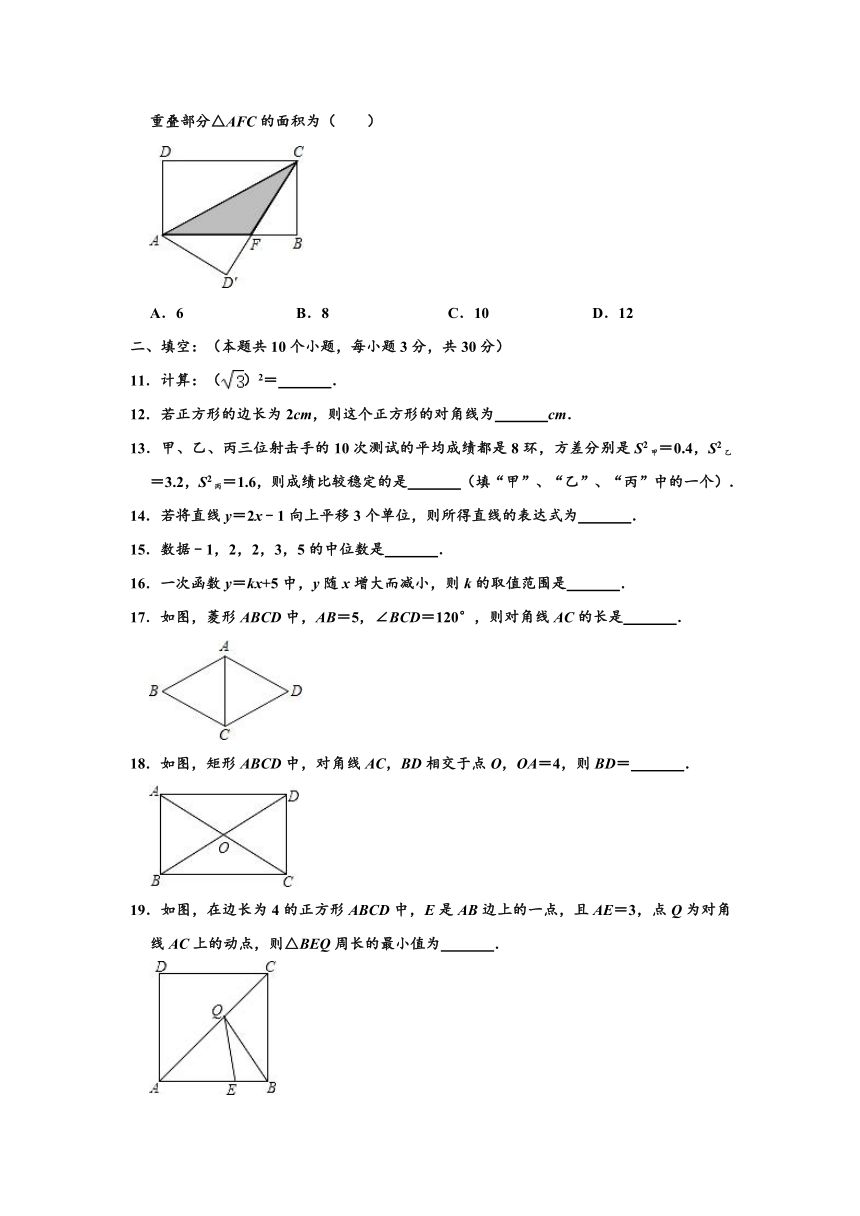
10.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )
A.6 B.8 C.10 D.12
二、填空:(本题共10个小题,每小题3分,共30分)
11.计算:()2= .
12.若正方形的边长为2cm,则这个正方形的对角线为 cm.
13.甲、乙、丙三位射击手的10次测试的平均成绩都是8环,方差分别是S2甲=0.4,S2乙=3.2,S2丙=1.6,则成绩比较稳定的是 (填“甲”、“乙”、“丙”中的一个).
14.若将直线y=2x﹣1向上平移3个单位,则所得直线的表达式为 .
15.数据﹣1,2,2,3,5的中位数是 .
16.一次函数y=kx+5中,y随x增大而减小,则k的取值范围是 .
17.如图,菱形ABCD中,AB=5,∠BCD=120°,则对角线AC的长是 .
18.如图,矩形ABCD中,对角线AC,BD相交于点O,OA=4,则BD= .
19.如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为 .
20.如图,直线y=kx+2(k<0)与x轴、y轴分别交于A,B两点,以AB为边向外作正方形ABCD,对角线AC,BD交于点E,则过O,E两点的直线解析式是 .
三、解答题(本题共8个小题,共60分)
21.计算:
(1)(2+)(2﹣)﹣(﹣)0;
(2)﹣(+2).
22.如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=3,求BC的长.
23.如图,直线AB与x轴交于点A(2,0),与y轴交于点B(0,﹣4).
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=6,求点C的坐标.
24.某地网课期间为了解初三3000名学生每天完成课外作业所用时间(单位:小时)情况,从中抽取了一部分学生进行了一次抽样调查,利用所得数据,绘制了直方图如下:(长方形的高表示该组人数,宽表示时间,每组中只含最低值不含最高值)解答下列问题:
(1)本次抽样调查共抽测了 名学生?
(2)这组数据的中位数落在 范围内?
(3)估计该地初三学生中有多少人完成课外作业时间不低于3.0小时.
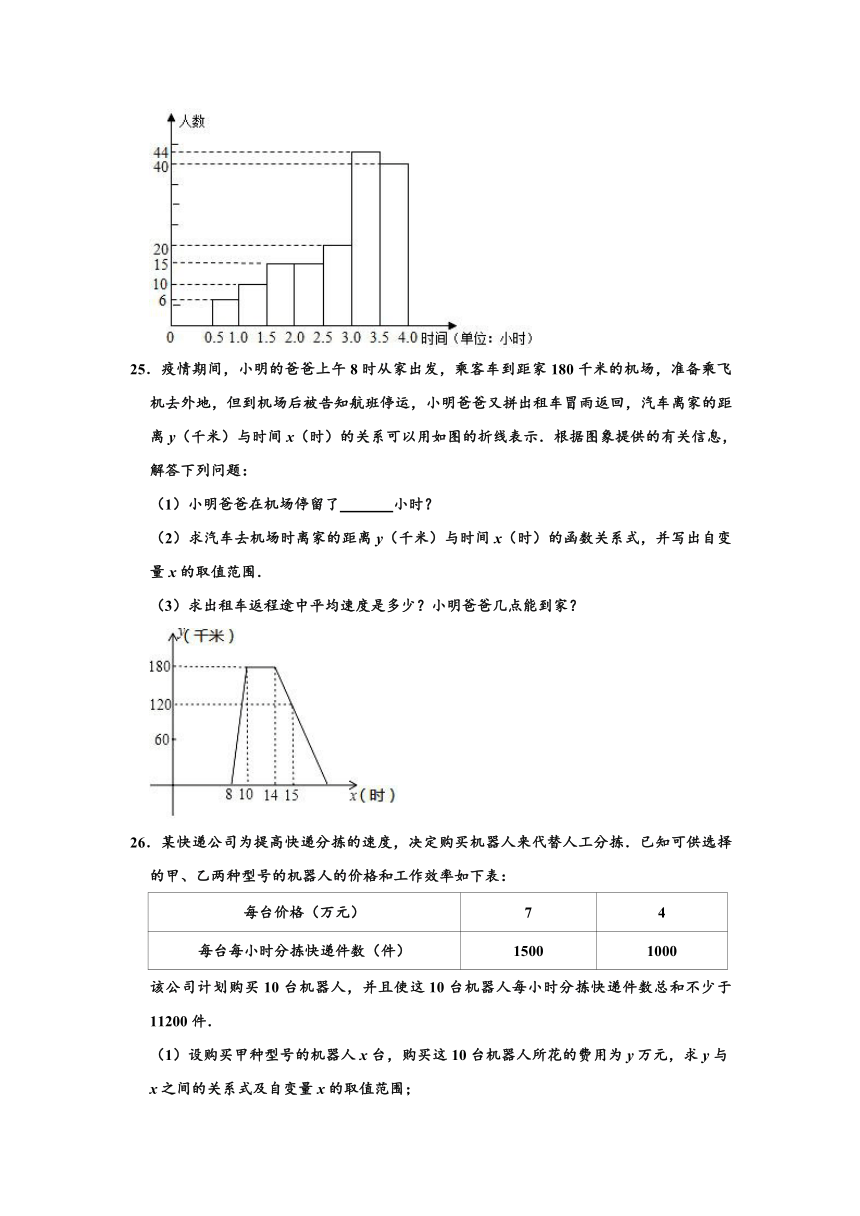
25.疫情期间,小明的爸爸上午8时从家出发,乘客车到距家180千米的机场,准备乘飞机去外地,但到机场后被告知航班停运,小明爸爸又拼出租车冒雨返回,汽车离家的距离y(千米)与时间x(时)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:
(1)小明爸爸在机场停留了 小时?
(2)求汽车去机场时离家的距离y(千米)与时间x(时)的函数关系式,并写出自变量x的取值范围.
(3)求出租车返程途中平均速度是多少?小明爸爸几点能到家?
26.某快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知可供选择的甲、乙两种型号的机器人的价格和工作效率如下表:
每台价格(万元) 7 4
每台每小时分拣快递件数(件) 1500 1000
该公司计划购买10台机器人,并且使这10台机器人每小时分拣快递件数总和不少于11200件.
(1)设购买甲种型号的机器人x台,购买这10台机器人所花的费用为y万元,求y与x之间的关系式及自变量x的取值范围;
(2)购买几台甲种型号的机器人,能使购买这10台机器人所花总费用最少?最少费用是多少?
27.如图①,正方形ADEF中,∠DAF=90°,点B、C分别在边AD、AF上,且AB=AC,此时显然BD=CF,BD⊥CF成立.
(1)如图②,当△ABC绕点A逆时针旋转α(0°<α<90°)时,那么BD=CF和BD⊥CF还成立吗?若成立,请证明;若不成立,请说明理由;
(2)如图③△ABC绕点A逆时针旋转45°时,延长DB交CF于点H;当AB=2,AD=+时,则线段FH的长为 .
28.如图,已知直线y=kx+b与直线y=﹣x﹣9平行,且y=kx+b还过点(2,3),与y轴交与A点.
(1)求A点坐标;
(2)若点P是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=MP,MB=OM,OE=ON,ND=NP,试证:四边形BCDE是平行四边形;
(3)在(2)的条件下,在直线y=kx+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,直接写出所有符合的点P的坐标;若不存在,请说明理由.
参考答案
一、单项选择题(本题共10个小题,每小题3分,共30分)请在答题卡上用2B铅笔将你的选项所对应的大写字母涂黑
1.函数y=的自变量x的取值范围是( )
A.x>2 B.x≥2 C.x≠2 D.x≤2
【分析】根据被开方数为非负数列出不等式,解之可得.
解:根据题意知x﹣2≥0,
解得:x≥2,
故选:B.
2.下列各式中,一定是二次根式的是( )
A. B. C. D.
【分析】含二次根号的式子,如果一定是二次根式,则不论字母取何值,被开方数一定是非负数.
解:A、是三次根式,故本选项不合题意;
B、,被开方数小于0,式子没有意义,故本选项不合题意;
C.是二次根式,故本选项符合题意;
D.,当x<0时,二次根式无意义,故本选项不合题意.
故选:C.
3.矩形、菱形、正方形都具有的性质是( )
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.对角线平分对角
【分析】利用特殊四边形的性质进而得出符合题意的答案.
解:矩形、菱形、正方形都具有的性质是对角线互相平分.
故选:B.
4.下列各组长度的线段中,可以组成直角三角形的是( )
A.1,2,3 B.3,4,5 C.1,,3 D.5,6,7
【分析】根据勾股定理的逆定理,可以判断各个选项中的三条线段是否能构成直角三角形,从而可以解答本题.
解:∵12+22≠32,故选项A中的三条线段不能构成直角三角形;
∵32+42=52,故选项B中的三条线段能构成直角三角形;
∵12+()2≠32,故选项C中的三条线段不能构成直角三角形;
∵52+62≠72,故选项D中的三条线段不能构成直角三角形;
故选:B.
5.顺次连接矩形的四边形中点所得的四边形一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
【分析】因为题中给出的条件是中点,所以可利用三角形中位线性质,以及矩形对角线相等去证明四条边都相等,从而说明是一个菱形.
解:连接AC、BD,
在△ABD中,
∵AH=HD,AE=EB
∴EH=BD,
同理FG=BD,HG=AC,EF=AC,
又∵在矩形ABCD中,AC=BD,
∴EH=HG=GF=FE,
∴四边形EFGH为菱形.
故选:C.
6.函数y=3x﹣5的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】一次项系数k=3>0,b=﹣5<0,则图象经过一、三、四象限,不经过第二象限.
解:∵k=3>0,b=﹣5<0,
∴图象经过一、三、四象限,不经过第二象限.
故选:B.
7.数据:a,1,2,3,6的平均数为3,则这组数据的众数是( )
A.2 B.0 C.4 D.3
【分析】先根据条件求出a的值,然后根据众数的定义就可解决问题.
解:∵数据a,1,2,3,6的平均数为3,
∴a+1+2+3+6=3×5=15,
解得a=3.
其中3出现的次数最多,
因而这组数据的众数是3.
故选:D.
8.一个正比例函数的图象经过点(﹣2,4),它的表达式为( )
A.y=﹣2x B.y=2x C.y=﹣x D.y=x
【分析】设该正比例函数的解析式为y=kx(k≠0),再把点(﹣2,4)代入求出k的值即可.
解:设该正比例函数的解析式为y=kx(k≠0),
∵正比例函数的图象经过点(﹣2,4),
∴4=﹣2k,解得k=﹣2,
∴这个正比例函数的表达式是y=﹣2x.
故选:A.
9.一次函数y1=kx+b与y2=x+a的图象如下图所示,则下列结论:①k<0;②a>0;③b>0;④当x<3时y1<y2.其中正确的个数( )
A.0 B.1 C.2 D.3
【分析】根据一次函数图象的性质对各小题分析后利用排除法求解.
解:根据图象y1=kx+b经过第一、二、四象限,
∴k<0,b>0,
故①③正确;
∵y2=x+a与y轴负半轴相交,
∴a<0,
故②错误;
当x<3时图象y1在y2的上方,应为当x<3时y1>y2,故④错误.
所以正确的有①③共2个.
故选:C.
10.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )
A.6 B.8 C.10 D.12
【分析】因为BC为AF边上的高,要求△AFC的面积,求得AF即可,求证△AFD′≌△CFB,得BF=D′F,设D′F=x,则在Rt△AFD′中,根据勾股定理求x,于是得到AF=AB﹣BF,即可得到结果.
解:易证△AFD′≌△CFB,
∴D′F=BF,
设D′F=x,则AF=8﹣x,
在Rt△AFD′中,(8﹣x)2=x2+42,
解之得:x=3,
∴AF=AB﹣FB=8﹣3=5,
∴S△AFC=?AF?BC=10.
故选:C.
二、填空:(本题共10个小题,每小题3分,共30分)
11.计算:()2= 3 .
【分析】原式利用平方根的性质判断即可.
解:原式=3,
故答案为:3
12.若正方形的边长为2cm,则这个正方形的对角线为 2 cm.
【分析】根据正方形的性质即可求出答案.
解:由勾股定理可知:对角线的长为=2,
故答案为:2.
13.甲、乙、丙三位射击手的10次测试的平均成绩都是8环,方差分别是S2甲=0.4,S2乙=3.2,S2丙=1.6,则成绩比较稳定的是 甲 (填“甲”、“乙”、“丙”中的一个).
【分析】直接利用方差的意义进而分析得出答案.
解:∵甲、乙、丙三位射击手的10次测试的平均成绩都是8环,方差分别是S2甲=0.4,S2乙=3.2,S2丙=1.6,
∴S2甲<S2丙<S2乙,
∴成绩比较稳定的是:甲.
故答案为:甲.
14.若将直线y=2x﹣1向上平移3个单位,则所得直线的表达式为 y=2x+2 .
【分析】直接根据“上加下减”的原则进行解答即可.
解:由“上加下减”的原则可知,将直线y=2x﹣1向上平移2个单位后,所得直线的表达式是y=2x﹣1+3,即y=2x+2.
故答案为:y=2x+2.
15.数据﹣1,2,2,3,5的中位数是 2 .
【分析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数.
解:将这5个数据重新排列为﹣1,2,2,3,5,
所以这组数据的中位数是2,
故答案为:2.
16.一次函数y=kx+5中,y随x增大而减小,则k的取值范围是 k<0 .
【分析】由y随x增大而减小,利用一次函数的性质可得出k<0.
解:∵在一次函数y=kx+5中,y随x增大而减小,
∴k<0.
故答案为:k<0.
17.如图,菱形ABCD中,AB=5,∠BCD=120°,则对角线AC的长是 5 .
【分析】根据菱形的性质及已知可得△ABC为等边三角形,从而得到AC=AB.
解:∵AB=BC,∠B+∠BCD=180°,∠BCD=120°,
∴∠B=60°
∴△ABC为等边三角形
∴AC=AB=5
故答案为:5.
18.如图,矩形ABCD中,对角线AC,BD相交于点O,OA=4,则BD= 8 .
【分析】由矩形的性质可得OA=OC=AC,BO=DO=BD,AC=BD,可得BD=2OA=8.
解:∵四边形ABCD是矩形,
∴OA=OC=AC,BO=DO=BD,AC=BD,
∴BD=2OA=8,
故答案为:8.
19.如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为 6 .
【分析】连接BD,DE,根据正方形的性质可知点B与点D关于直线AC对称,故DE的长即为BQ+QE的最小值,进而可得出结论.
解:连接BD,DE,
∵四边形ABCD是正方形,
∴点B与点D关于直线AC对称,
∴DE的长即为BQ+QE的最小值,
∵DE=BQ+QE===5,
∴△BEQ周长的最小值=DE+BE=5+1=6.
故答案为:6.
20.如图,直线y=kx+2(k<0)与x轴、y轴分别交于A,B两点,以AB为边向外作正方形ABCD,对角线AC,BD交于点E,则过O,E两点的直线解析式是 y=x .
【分析】根据图象上点的坐标特征求得A、B的坐标,然后通过证得△AOB≌△DMA,得出D的坐标,即可求得E的坐标,根据E的坐标即可求得直线OE的解析式.
解:∵直线y=kx+2(k<0)与x轴、y轴分别交于A,B两点,
∴A(﹣,0),B(0,2),
∴OA=﹣,OB=2,
作DM⊥x轴于M,
∵正方形ABCD中,∠BAD=90°,AB=AD,
∴∠BAO+∠DAM=90°,
∵∠BAO+∠ABO=90°,
在△AOB和△DMA中
,
∴△AOB≌△DMA(AAS),
∴AM=OB=2,DM=OA=﹣,
∴D(2﹣,﹣),
∵四边形ABCD是正方形,
∴E是BD的中点,
∴E(1﹣,1﹣),
∴过O,E两点的直线解析式是y=x,
故答案为y=x.
三、解答题(本题共8个小题,共60分)
21.计算:
(1)(2+)(2﹣)﹣(﹣)0;
(2)﹣(+2).
【分析】(1)直接利用乘法公式结合零指数幂的性质化简得出答案;
(2)直接利用二次根式的乘法运算法则计算得出答案.
解:(1)原式=22﹣()2﹣1
=4﹣3﹣1
=0;
(2)原式=2﹣2﹣2
=﹣2.
22.如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=3,求BC的长.
【分析】分别解两个直角三角形,即可求出BD、CD的长,进而求出BC.
解:∵AD⊥BC∴∠ADB=∠ADC=90°,
在 Rt△ABD 中∵∠B=45°且AD=3,
∴∠BAD=∠B=45°,
∴BD=AD=3,
在 Rt△ACD 中,∠C=30°
∴CD=AD=3,
∴BC=BD+CD=3+3.
23.如图,直线AB与x轴交于点A(2,0),与y轴交于点B(0,﹣4).
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=6,求点C的坐标.
【分析】(1)设直线AB的解析式为:y=kx+b,把点A(2,0)与点B(0,﹣4)解方程组即可得到结论;
(2)设点C的坐标(a,2a﹣4),根据三角形的面积公式列方程即可得到结论.
解:(1)设直线AB的解析式为:y=kx+b,
把点A(2,0)与点B(0,﹣4)代入得,,
∴,
∴直线AB的解析式为:y=2x﹣4;
(2)设点C的坐标(a,2a﹣4),
∵S△BOC=6,
∴×4×a=6,
∴a=3,
∴点C的坐标为:(3,2).
24.某地网课期间为了解初三3000名学生每天完成课外作业所用时间(单位:小时)情况,从中抽取了一部分学生进行了一次抽样调查,利用所得数据,绘制了直方图如下:(长方形的高表示该组人数,宽表示时间,每组中只含最低值不含最高值)解答下列问题:
(1)本次抽样调查共抽测了 150 名学生?
(2)这组数据的中位数落在 3.0~3.5 范围内?
(3)估计该地初三学生中有多少人完成课外作业时间不低于3.0小时.
【分析】(1)各组频数之和就是得出人数;
(2)将150个数据从小到大排列后,找出第75、76位的数落在哪组,即可确定中位数在哪组;
(3)样本估计总体,样本中时间不低于3.0小时的占,因此估计3000人的是符合条件的人数.
解:(1)6+10+15+15+20+44+40=150 (人),
故答案为:150;
(2)把150人的成绩从小到大排列后,处在第75、76位的两个数都在3.0~3.5这组,因此中位数在3.0~3.5这组,
故答案为:3.0~3.5;
(3)3000×=1680(人),
答:有1680人完成课外作业时间不低于3.0小时.
25.疫情期间,小明的爸爸上午8时从家出发,乘客车到距家180千米的机场,准备乘飞机去外地,但到机场后被告知航班停运,小明爸爸又拼出租车冒雨返回,汽车离家的距离y(千米)与时间x(时)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:
(1)小明爸爸在机场停留了 4 小时?
(2)求汽车去机场时离家的距离y(千米)与时间x(时)的函数关系式,并写出自变量x的取值范围.
(3)求出租车返程途中平均速度是多少?小明爸爸几点能到家?
【分析】(1)根据函数图象中的数据,可以得到小明爸爸在机场停留了几个小时;
(2)根据函数图象中的数据,可以得到汽车去机场时离家的距离y(千米)与时间x(时)的函数关系式,并写出自变量x的取值范围;
(3)根据函数图象中的数据,可以计算出出租车返程途中平均速度是多少,小明爸爸几点能到家.
解:(1)由图象可得,
小明爸爸在机场停留了14﹣10=4(小时),
故答案为:4;
(2)设汽车去机场时离家的距离y(千米)与时间x(时)的函数关系式是y=kx+b,
,
解得,,
即汽车去机场时离家的距离y(千米)与时间x(时)的函数关系式是y=90x﹣720(8≤x≤10);
(3)(180﹣120)÷(15﹣14)=60(千米/小时),
180÷60=3(小时),
14+3=17,
答:出租车返程途中平均速度是60千米/小时,小明爸爸17点能到家.
26.某快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知可供选择的甲、乙两种型号的机器人的价格和工作效率如下表:
每台价格(万元) 7 4
每台每小时分拣快递件数(件) 1500 1000
该公司计划购买10台机器人,并且使这10台机器人每小时分拣快递件数总和不少于11200件.
(1)设购买甲种型号的机器人x台,购买这10台机器人所花的费用为y万元,求y与x之间的关系式及自变量x的取值范围;
(2)购买几台甲种型号的机器人,能使购买这10台机器人所花总费用最少?最少费用是多少?
【分析】(1)根据题意和表格中的数据,可以得到y与x之间的关系式,再根据这10台机器人每小时分拣快递件数总和不少于11200件,可以得到x的取值范围;
(2)根据(1)中的结果,利用一次函数的性质,可以得到y的最小值,本题得以解决.
解:(1)由题意可得,
y=7x+4(10﹣x)=3x+40,
∵这10台机器人每小时分拣快递件数总和不少于11200件,
∴1500x+1000(10﹣x)≥11200,且0≤x≤10,
解得,2.4≤x≤10,
又∵x为整数,
∴3≤x≤10,
即y与x的函数关系式为y=3x+40(3≤x≤10,x为整数);
(2)∵y=3x+40,
∴k=3>0,y随x的增大而增大,
∵3≤x≤10,x为整数
∴当x=3时,y取得最小值,此时y=49,10﹣x=7,
答:买甲型机器人3台,乙型机器人7台时,所需费用最少,最少费用是49万元.
27.如图①,正方形ADEF中,∠DAF=90°,点B、C分别在边AD、AF上,且AB=AC,此时显然BD=CF,BD⊥CF成立.
(1)如图②,当△ABC绕点A逆时针旋转α(0°<α<90°)时,那么BD=CF和BD⊥CF还成立吗?若成立,请证明;若不成立,请说明理由;
(2)如图③△ABC绕点A逆时针旋转45°时,延长DB交CF于点H;当AB=2,AD=+时,则线段FH的长为 .
【分析】(1)根据正方形的性质得到AD=AF,∠DAF=90°,根据全等三角形的性质得到BD=CF,如图②,延长DB交AF于点O,交FC于点G,求得∠ADB=∠AFC于是得到结论;
(2)如图③,过B作作BM⊥AD于M,连接BF,BC交AF于点P,同(1)的方法得,CF=BD,BD⊥CF,根据等腰直角三角形的性质得到AM=BM=,DM=,在Rt△BDM中,根据勾股定理得,BD=,求得BD=BF=CF=,根据勾股定理即可得到结论.
解:(1)BD=CF,BD⊥CF还成立,
理由如下:∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵△ABC中,AB=AC,∠BAC=90°,
∴∠DAB=∠FAC,
∴△ADB≌△AFC(SAS),
∴BD=CF,
如图②,延长DB交AF于点O,交FC于点G,
∴∠FOG=∠AOD,
∵△ADB≌△AFC,
∴∠ADB=∠AFC
∴∠FGO=∠FAD=90°,
∴BD⊥CF;
(2)如图③,过B作作BM⊥AD于M,连接BF,BC交AF于点P,
同(1)的方法得,CF=BD,BD⊥CF,
在Rt△AMB中,∵∠BAM=45°,AB=2,
∴AM=BM=,DM=,
在Rt△BDM中,根据勾股定理得,BD=,
∴BD=BF=CF=,
由已知可得CB=AB=2,
∴FP=,
在△BCF中,由面积得BH×CF=FP×BC,
∴BH=,
∴FH===,
故答案为:.
28.如图,已知直线y=kx+b与直线y=﹣x﹣9平行,且y=kx+b还过点(2,3),与y轴交与A点.
(1)求A点坐标;
(2)若点P是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=MP,MB=OM,OE=ON,ND=NP,试证:四边形BCDE是平行四边形;
(3)在(2)的条件下,在直线y=kx+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,直接写出所有符合的点P的坐标;若不存在,请说明理由.
【分析】(1)直线y=kx+b与y=﹣x﹣9平行,且过点A(2,3),则,即可求解;
(2)证明△OBE≌△PDC(SAS)、△MBC≌△NDE(SAS),即可求解;
(3)证明△DPC≌△CMB(AAS),则CM=PD,即可求解.
解:(1)∵直线y=kx+b与y=﹣x﹣9平行,且过点A(2,3),
则,解得,
∴一次函数解析式为y=﹣x+4,
当x=0时,y=4,
∴A点坐标是(0,4);
(2)证明:∵PM⊥x轴,PN⊥y轴,
∴∠M=∠N=∠O=90°,
∴四边形PMON是矩形,
∴PM=ON,OM=PN,∠M=∠O=∠N=∠P=90°.
∵PC=MP,MB=OM,OE=ON,ND=NP,
∴PC=OE,CM=NE,ND=BM,PD=OB,
在△OBE和△PDC中,OB=PD,∠O=∠CPD,OE=PC,
∴△OBE≌△PDC(SAS),
∴DC=BE,
同理可证△MBC≌△NDE(SAS),
∴DE=BC.
∴四边形BCDE是平行四边形;
(3)存在这样的点P,理由:
设点P(m,﹣m+4),
则CM=PC=|(4﹣m)|=|﹣m|,PD=m,
当四边形BCDE为正方形时,则∠DCB=90°,DC=BC,
而∠CBM+∠MCB=90°,∠MCB+∠DCP=90°,
∴∠CBM=∠DCP,
而∠DPC=∠CMB=90°,
∴△DPC≌△CMB(AAS),
∴CM=PD,
即=|﹣m|=m,解得:m=或﹣8,
故P点坐标是(,)或(﹣8,8).
一、选择题(共10小题).
1.函数y=的自变量x的取值范围是( )
A.x>2 B.x≥2 C.x≠2 D.x≤2
2.下列各式中,一定是二次根式的是( )
A. B. C. D.
3.矩形、菱形、正方形都具有的性质是( )
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.对角线平分对角
4.下列各组长度的线段中,可以组成直角三角形的是( )
A.1,2,3 B.3,4,5 C.1,,3 D.5,6,7
5.顺次连接矩形的四边形中点所得的四边形一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
6.函数y=3x﹣5的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.数据:a,1,2,3,6的平均数为3,则这组数据的众数是( )
A.2 B.0 C.4 D.3
8.一个正比例函数的图象经过点(﹣2,4),它的表达式为( )
A.y=﹣2x B.y=2x C.y=﹣x D.y=x
9.一次函数y1=kx+b与y2=x+a的图象如下图所示,则下列结论:①k<0;②a>0;③b>0;④当x<3时y1<y2.其中正确的个数( )
A.0 B.1 C.2 D.3
10.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )
A.6 B.8 C.10 D.12
二、填空:(本题共10个小题,每小题3分,共30分)
11.计算:()2= .
12.若正方形的边长为2cm,则这个正方形的对角线为 cm.
13.甲、乙、丙三位射击手的10次测试的平均成绩都是8环,方差分别是S2甲=0.4,S2乙=3.2,S2丙=1.6,则成绩比较稳定的是 (填“甲”、“乙”、“丙”中的一个).
14.若将直线y=2x﹣1向上平移3个单位,则所得直线的表达式为 .
15.数据﹣1,2,2,3,5的中位数是 .
16.一次函数y=kx+5中,y随x增大而减小,则k的取值范围是 .
17.如图,菱形ABCD中,AB=5,∠BCD=120°,则对角线AC的长是 .
18.如图,矩形ABCD中,对角线AC,BD相交于点O,OA=4,则BD= .
19.如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为 .
20.如图,直线y=kx+2(k<0)与x轴、y轴分别交于A,B两点,以AB为边向外作正方形ABCD,对角线AC,BD交于点E,则过O,E两点的直线解析式是 .
三、解答题(本题共8个小题,共60分)
21.计算:
(1)(2+)(2﹣)﹣(﹣)0;
(2)﹣(+2).
22.如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=3,求BC的长.
23.如图,直线AB与x轴交于点A(2,0),与y轴交于点B(0,﹣4).
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=6,求点C的坐标.
24.某地网课期间为了解初三3000名学生每天完成课外作业所用时间(单位:小时)情况,从中抽取了一部分学生进行了一次抽样调查,利用所得数据,绘制了直方图如下:(长方形的高表示该组人数,宽表示时间,每组中只含最低值不含最高值)解答下列问题:
(1)本次抽样调查共抽测了 名学生?
(2)这组数据的中位数落在 范围内?
(3)估计该地初三学生中有多少人完成课外作业时间不低于3.0小时.
25.疫情期间,小明的爸爸上午8时从家出发,乘客车到距家180千米的机场,准备乘飞机去外地,但到机场后被告知航班停运,小明爸爸又拼出租车冒雨返回,汽车离家的距离y(千米)与时间x(时)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:
(1)小明爸爸在机场停留了 小时?
(2)求汽车去机场时离家的距离y(千米)与时间x(时)的函数关系式,并写出自变量x的取值范围.
(3)求出租车返程途中平均速度是多少?小明爸爸几点能到家?
26.某快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知可供选择的甲、乙两种型号的机器人的价格和工作效率如下表:
每台价格(万元) 7 4
每台每小时分拣快递件数(件) 1500 1000
该公司计划购买10台机器人,并且使这10台机器人每小时分拣快递件数总和不少于11200件.
(1)设购买甲种型号的机器人x台,购买这10台机器人所花的费用为y万元,求y与x之间的关系式及自变量x的取值范围;
(2)购买几台甲种型号的机器人,能使购买这10台机器人所花总费用最少?最少费用是多少?
27.如图①,正方形ADEF中,∠DAF=90°,点B、C分别在边AD、AF上,且AB=AC,此时显然BD=CF,BD⊥CF成立.
(1)如图②,当△ABC绕点A逆时针旋转α(0°<α<90°)时,那么BD=CF和BD⊥CF还成立吗?若成立,请证明;若不成立,请说明理由;
(2)如图③△ABC绕点A逆时针旋转45°时,延长DB交CF于点H;当AB=2,AD=+时,则线段FH的长为 .
28.如图,已知直线y=kx+b与直线y=﹣x﹣9平行,且y=kx+b还过点(2,3),与y轴交与A点.
(1)求A点坐标;
(2)若点P是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=MP,MB=OM,OE=ON,ND=NP,试证:四边形BCDE是平行四边形;
(3)在(2)的条件下,在直线y=kx+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,直接写出所有符合的点P的坐标;若不存在,请说明理由.
参考答案
一、单项选择题(本题共10个小题,每小题3分,共30分)请在答题卡上用2B铅笔将你的选项所对应的大写字母涂黑
1.函数y=的自变量x的取值范围是( )
A.x>2 B.x≥2 C.x≠2 D.x≤2
【分析】根据被开方数为非负数列出不等式,解之可得.
解:根据题意知x﹣2≥0,
解得:x≥2,
故选:B.
2.下列各式中,一定是二次根式的是( )
A. B. C. D.
【分析】含二次根号的式子,如果一定是二次根式,则不论字母取何值,被开方数一定是非负数.
解:A、是三次根式,故本选项不合题意;
B、,被开方数小于0,式子没有意义,故本选项不合题意;
C.是二次根式,故本选项符合题意;
D.,当x<0时,二次根式无意义,故本选项不合题意.
故选:C.
3.矩形、菱形、正方形都具有的性质是( )
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.对角线平分对角
【分析】利用特殊四边形的性质进而得出符合题意的答案.
解:矩形、菱形、正方形都具有的性质是对角线互相平分.
故选:B.
4.下列各组长度的线段中,可以组成直角三角形的是( )
A.1,2,3 B.3,4,5 C.1,,3 D.5,6,7
【分析】根据勾股定理的逆定理,可以判断各个选项中的三条线段是否能构成直角三角形,从而可以解答本题.
解:∵12+22≠32,故选项A中的三条线段不能构成直角三角形;
∵32+42=52,故选项B中的三条线段能构成直角三角形;
∵12+()2≠32,故选项C中的三条线段不能构成直角三角形;
∵52+62≠72,故选项D中的三条线段不能构成直角三角形;
故选:B.
5.顺次连接矩形的四边形中点所得的四边形一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
【分析】因为题中给出的条件是中点,所以可利用三角形中位线性质,以及矩形对角线相等去证明四条边都相等,从而说明是一个菱形.
解:连接AC、BD,
在△ABD中,
∵AH=HD,AE=EB
∴EH=BD,
同理FG=BD,HG=AC,EF=AC,
又∵在矩形ABCD中,AC=BD,
∴EH=HG=GF=FE,
∴四边形EFGH为菱形.
故选:C.
6.函数y=3x﹣5的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】一次项系数k=3>0,b=﹣5<0,则图象经过一、三、四象限,不经过第二象限.
解:∵k=3>0,b=﹣5<0,
∴图象经过一、三、四象限,不经过第二象限.
故选:B.
7.数据:a,1,2,3,6的平均数为3,则这组数据的众数是( )
A.2 B.0 C.4 D.3
【分析】先根据条件求出a的值,然后根据众数的定义就可解决问题.
解:∵数据a,1,2,3,6的平均数为3,
∴a+1+2+3+6=3×5=15,
解得a=3.
其中3出现的次数最多,
因而这组数据的众数是3.
故选:D.
8.一个正比例函数的图象经过点(﹣2,4),它的表达式为( )
A.y=﹣2x B.y=2x C.y=﹣x D.y=x
【分析】设该正比例函数的解析式为y=kx(k≠0),再把点(﹣2,4)代入求出k的值即可.
解:设该正比例函数的解析式为y=kx(k≠0),
∵正比例函数的图象经过点(﹣2,4),
∴4=﹣2k,解得k=﹣2,
∴这个正比例函数的表达式是y=﹣2x.
故选:A.
9.一次函数y1=kx+b与y2=x+a的图象如下图所示,则下列结论:①k<0;②a>0;③b>0;④当x<3时y1<y2.其中正确的个数( )
A.0 B.1 C.2 D.3
【分析】根据一次函数图象的性质对各小题分析后利用排除法求解.
解:根据图象y1=kx+b经过第一、二、四象限,
∴k<0,b>0,
故①③正确;
∵y2=x+a与y轴负半轴相交,
∴a<0,
故②错误;
当x<3时图象y1在y2的上方,应为当x<3时y1>y2,故④错误.
所以正确的有①③共2个.
故选:C.
10.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )
A.6 B.8 C.10 D.12
【分析】因为BC为AF边上的高,要求△AFC的面积,求得AF即可,求证△AFD′≌△CFB,得BF=D′F,设D′F=x,则在Rt△AFD′中,根据勾股定理求x,于是得到AF=AB﹣BF,即可得到结果.
解:易证△AFD′≌△CFB,
∴D′F=BF,
设D′F=x,则AF=8﹣x,
在Rt△AFD′中,(8﹣x)2=x2+42,
解之得:x=3,
∴AF=AB﹣FB=8﹣3=5,
∴S△AFC=?AF?BC=10.
故选:C.
二、填空:(本题共10个小题,每小题3分,共30分)
11.计算:()2= 3 .
【分析】原式利用平方根的性质判断即可.
解:原式=3,
故答案为:3
12.若正方形的边长为2cm,则这个正方形的对角线为 2 cm.
【分析】根据正方形的性质即可求出答案.
解:由勾股定理可知:对角线的长为=2,
故答案为:2.
13.甲、乙、丙三位射击手的10次测试的平均成绩都是8环,方差分别是S2甲=0.4,S2乙=3.2,S2丙=1.6,则成绩比较稳定的是 甲 (填“甲”、“乙”、“丙”中的一个).
【分析】直接利用方差的意义进而分析得出答案.
解:∵甲、乙、丙三位射击手的10次测试的平均成绩都是8环,方差分别是S2甲=0.4,S2乙=3.2,S2丙=1.6,
∴S2甲<S2丙<S2乙,
∴成绩比较稳定的是:甲.
故答案为:甲.
14.若将直线y=2x﹣1向上平移3个单位,则所得直线的表达式为 y=2x+2 .
【分析】直接根据“上加下减”的原则进行解答即可.
解:由“上加下减”的原则可知,将直线y=2x﹣1向上平移2个单位后,所得直线的表达式是y=2x﹣1+3,即y=2x+2.
故答案为:y=2x+2.
15.数据﹣1,2,2,3,5的中位数是 2 .
【分析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数.
解:将这5个数据重新排列为﹣1,2,2,3,5,
所以这组数据的中位数是2,
故答案为:2.
16.一次函数y=kx+5中,y随x增大而减小,则k的取值范围是 k<0 .
【分析】由y随x增大而减小,利用一次函数的性质可得出k<0.
解:∵在一次函数y=kx+5中,y随x增大而减小,
∴k<0.
故答案为:k<0.
17.如图,菱形ABCD中,AB=5,∠BCD=120°,则对角线AC的长是 5 .
【分析】根据菱形的性质及已知可得△ABC为等边三角形,从而得到AC=AB.
解:∵AB=BC,∠B+∠BCD=180°,∠BCD=120°,
∴∠B=60°
∴△ABC为等边三角形
∴AC=AB=5
故答案为:5.
18.如图,矩形ABCD中,对角线AC,BD相交于点O,OA=4,则BD= 8 .
【分析】由矩形的性质可得OA=OC=AC,BO=DO=BD,AC=BD,可得BD=2OA=8.
解:∵四边形ABCD是矩形,
∴OA=OC=AC,BO=DO=BD,AC=BD,
∴BD=2OA=8,
故答案为:8.
19.如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为 6 .
【分析】连接BD,DE,根据正方形的性质可知点B与点D关于直线AC对称,故DE的长即为BQ+QE的最小值,进而可得出结论.
解:连接BD,DE,
∵四边形ABCD是正方形,
∴点B与点D关于直线AC对称,
∴DE的长即为BQ+QE的最小值,
∵DE=BQ+QE===5,
∴△BEQ周长的最小值=DE+BE=5+1=6.
故答案为:6.
20.如图,直线y=kx+2(k<0)与x轴、y轴分别交于A,B两点,以AB为边向外作正方形ABCD,对角线AC,BD交于点E,则过O,E两点的直线解析式是 y=x .
【分析】根据图象上点的坐标特征求得A、B的坐标,然后通过证得△AOB≌△DMA,得出D的坐标,即可求得E的坐标,根据E的坐标即可求得直线OE的解析式.
解:∵直线y=kx+2(k<0)与x轴、y轴分别交于A,B两点,
∴A(﹣,0),B(0,2),
∴OA=﹣,OB=2,
作DM⊥x轴于M,
∵正方形ABCD中,∠BAD=90°,AB=AD,
∴∠BAO+∠DAM=90°,
∵∠BAO+∠ABO=90°,
在△AOB和△DMA中
,
∴△AOB≌△DMA(AAS),
∴AM=OB=2,DM=OA=﹣,
∴D(2﹣,﹣),
∵四边形ABCD是正方形,
∴E是BD的中点,
∴E(1﹣,1﹣),
∴过O,E两点的直线解析式是y=x,
故答案为y=x.
三、解答题(本题共8个小题,共60分)
21.计算:
(1)(2+)(2﹣)﹣(﹣)0;
(2)﹣(+2).
【分析】(1)直接利用乘法公式结合零指数幂的性质化简得出答案;
(2)直接利用二次根式的乘法运算法则计算得出答案.
解:(1)原式=22﹣()2﹣1
=4﹣3﹣1
=0;
(2)原式=2﹣2﹣2
=﹣2.
22.如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=3,求BC的长.
【分析】分别解两个直角三角形,即可求出BD、CD的长,进而求出BC.
解:∵AD⊥BC∴∠ADB=∠ADC=90°,
在 Rt△ABD 中∵∠B=45°且AD=3,
∴∠BAD=∠B=45°,
∴BD=AD=3,
在 Rt△ACD 中,∠C=30°
∴CD=AD=3,
∴BC=BD+CD=3+3.
23.如图,直线AB与x轴交于点A(2,0),与y轴交于点B(0,﹣4).
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=6,求点C的坐标.
【分析】(1)设直线AB的解析式为:y=kx+b,把点A(2,0)与点B(0,﹣4)解方程组即可得到结论;
(2)设点C的坐标(a,2a﹣4),根据三角形的面积公式列方程即可得到结论.
解:(1)设直线AB的解析式为:y=kx+b,
把点A(2,0)与点B(0,﹣4)代入得,,
∴,
∴直线AB的解析式为:y=2x﹣4;
(2)设点C的坐标(a,2a﹣4),
∵S△BOC=6,
∴×4×a=6,
∴a=3,
∴点C的坐标为:(3,2).
24.某地网课期间为了解初三3000名学生每天完成课外作业所用时间(单位:小时)情况,从中抽取了一部分学生进行了一次抽样调查,利用所得数据,绘制了直方图如下:(长方形的高表示该组人数,宽表示时间,每组中只含最低值不含最高值)解答下列问题:
(1)本次抽样调查共抽测了 150 名学生?
(2)这组数据的中位数落在 3.0~3.5 范围内?
(3)估计该地初三学生中有多少人完成课外作业时间不低于3.0小时.
【分析】(1)各组频数之和就是得出人数;
(2)将150个数据从小到大排列后,找出第75、76位的数落在哪组,即可确定中位数在哪组;
(3)样本估计总体,样本中时间不低于3.0小时的占,因此估计3000人的是符合条件的人数.
解:(1)6+10+15+15+20+44+40=150 (人),
故答案为:150;
(2)把150人的成绩从小到大排列后,处在第75、76位的两个数都在3.0~3.5这组,因此中位数在3.0~3.5这组,
故答案为:3.0~3.5;
(3)3000×=1680(人),
答:有1680人完成课外作业时间不低于3.0小时.
25.疫情期间,小明的爸爸上午8时从家出发,乘客车到距家180千米的机场,准备乘飞机去外地,但到机场后被告知航班停运,小明爸爸又拼出租车冒雨返回,汽车离家的距离y(千米)与时间x(时)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:
(1)小明爸爸在机场停留了 4 小时?
(2)求汽车去机场时离家的距离y(千米)与时间x(时)的函数关系式,并写出自变量x的取值范围.
(3)求出租车返程途中平均速度是多少?小明爸爸几点能到家?
【分析】(1)根据函数图象中的数据,可以得到小明爸爸在机场停留了几个小时;
(2)根据函数图象中的数据,可以得到汽车去机场时离家的距离y(千米)与时间x(时)的函数关系式,并写出自变量x的取值范围;
(3)根据函数图象中的数据,可以计算出出租车返程途中平均速度是多少,小明爸爸几点能到家.
解:(1)由图象可得,
小明爸爸在机场停留了14﹣10=4(小时),
故答案为:4;
(2)设汽车去机场时离家的距离y(千米)与时间x(时)的函数关系式是y=kx+b,
,
解得,,
即汽车去机场时离家的距离y(千米)与时间x(时)的函数关系式是y=90x﹣720(8≤x≤10);
(3)(180﹣120)÷(15﹣14)=60(千米/小时),
180÷60=3(小时),
14+3=17,
答:出租车返程途中平均速度是60千米/小时,小明爸爸17点能到家.
26.某快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知可供选择的甲、乙两种型号的机器人的价格和工作效率如下表:
每台价格(万元) 7 4
每台每小时分拣快递件数(件) 1500 1000
该公司计划购买10台机器人,并且使这10台机器人每小时分拣快递件数总和不少于11200件.
(1)设购买甲种型号的机器人x台,购买这10台机器人所花的费用为y万元,求y与x之间的关系式及自变量x的取值范围;
(2)购买几台甲种型号的机器人,能使购买这10台机器人所花总费用最少?最少费用是多少?
【分析】(1)根据题意和表格中的数据,可以得到y与x之间的关系式,再根据这10台机器人每小时分拣快递件数总和不少于11200件,可以得到x的取值范围;
(2)根据(1)中的结果,利用一次函数的性质,可以得到y的最小值,本题得以解决.
解:(1)由题意可得,
y=7x+4(10﹣x)=3x+40,
∵这10台机器人每小时分拣快递件数总和不少于11200件,
∴1500x+1000(10﹣x)≥11200,且0≤x≤10,
解得,2.4≤x≤10,
又∵x为整数,
∴3≤x≤10,
即y与x的函数关系式为y=3x+40(3≤x≤10,x为整数);
(2)∵y=3x+40,
∴k=3>0,y随x的增大而增大,
∵3≤x≤10,x为整数
∴当x=3时,y取得最小值,此时y=49,10﹣x=7,
答:买甲型机器人3台,乙型机器人7台时,所需费用最少,最少费用是49万元.
27.如图①,正方形ADEF中,∠DAF=90°,点B、C分别在边AD、AF上,且AB=AC,此时显然BD=CF,BD⊥CF成立.
(1)如图②,当△ABC绕点A逆时针旋转α(0°<α<90°)时,那么BD=CF和BD⊥CF还成立吗?若成立,请证明;若不成立,请说明理由;
(2)如图③△ABC绕点A逆时针旋转45°时,延长DB交CF于点H;当AB=2,AD=+时,则线段FH的长为 .
【分析】(1)根据正方形的性质得到AD=AF,∠DAF=90°,根据全等三角形的性质得到BD=CF,如图②,延长DB交AF于点O,交FC于点G,求得∠ADB=∠AFC于是得到结论;
(2)如图③,过B作作BM⊥AD于M,连接BF,BC交AF于点P,同(1)的方法得,CF=BD,BD⊥CF,根据等腰直角三角形的性质得到AM=BM=,DM=,在Rt△BDM中,根据勾股定理得,BD=,求得BD=BF=CF=,根据勾股定理即可得到结论.
解:(1)BD=CF,BD⊥CF还成立,
理由如下:∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵△ABC中,AB=AC,∠BAC=90°,
∴∠DAB=∠FAC,
∴△ADB≌△AFC(SAS),
∴BD=CF,
如图②,延长DB交AF于点O,交FC于点G,
∴∠FOG=∠AOD,
∵△ADB≌△AFC,
∴∠ADB=∠AFC
∴∠FGO=∠FAD=90°,
∴BD⊥CF;
(2)如图③,过B作作BM⊥AD于M,连接BF,BC交AF于点P,
同(1)的方法得,CF=BD,BD⊥CF,
在Rt△AMB中,∵∠BAM=45°,AB=2,
∴AM=BM=,DM=,
在Rt△BDM中,根据勾股定理得,BD=,
∴BD=BF=CF=,
由已知可得CB=AB=2,
∴FP=,
在△BCF中,由面积得BH×CF=FP×BC,
∴BH=,
∴FH===,
故答案为:.
28.如图,已知直线y=kx+b与直线y=﹣x﹣9平行,且y=kx+b还过点(2,3),与y轴交与A点.
(1)求A点坐标;
(2)若点P是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=MP,MB=OM,OE=ON,ND=NP,试证:四边形BCDE是平行四边形;
(3)在(2)的条件下,在直线y=kx+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,直接写出所有符合的点P的坐标;若不存在,请说明理由.
【分析】(1)直线y=kx+b与y=﹣x﹣9平行,且过点A(2,3),则,即可求解;
(2)证明△OBE≌△PDC(SAS)、△MBC≌△NDE(SAS),即可求解;
(3)证明△DPC≌△CMB(AAS),则CM=PD,即可求解.
解:(1)∵直线y=kx+b与y=﹣x﹣9平行,且过点A(2,3),
则,解得,
∴一次函数解析式为y=﹣x+4,
当x=0时,y=4,
∴A点坐标是(0,4);
(2)证明:∵PM⊥x轴,PN⊥y轴,
∴∠M=∠N=∠O=90°,
∴四边形PMON是矩形,
∴PM=ON,OM=PN,∠M=∠O=∠N=∠P=90°.
∵PC=MP,MB=OM,OE=ON,ND=NP,
∴PC=OE,CM=NE,ND=BM,PD=OB,
在△OBE和△PDC中,OB=PD,∠O=∠CPD,OE=PC,
∴△OBE≌△PDC(SAS),
∴DC=BE,
同理可证△MBC≌△NDE(SAS),
∴DE=BC.
∴四边形BCDE是平行四边形;
(3)存在这样的点P,理由:
设点P(m,﹣m+4),
则CM=PC=|(4﹣m)|=|﹣m|,PD=m,
当四边形BCDE为正方形时,则∠DCB=90°,DC=BC,
而∠CBM+∠MCB=90°,∠MCB+∠DCP=90°,
∴∠CBM=∠DCP,
而∠DPC=∠CMB=90°,
∴△DPC≌△CMB(AAS),
∴CM=PD,
即=|﹣m|=m,解得:m=或﹣8,
故P点坐标是(,)或(﹣8,8).
同课章节目录
