11.1.1 三角形的边课时达标(含答案)
文档属性
| 名称 | 11.1.1 三角形的边课时达标(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-21 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
11.1.1三角形课时达标
选择题
1、三角形是(??
)
A.连接任意三个角组成的图形
B.由不在同一条直线上的三条线段首尾顺次相接所组成的图形
C.由三条线段组成的图形
D.以上说法均不对
2、如图所示,其中三角形的个数是( )
A.2个????
B.3个????
C.4个????
D.5个
3、下列长度的三根木棒首尾相接,不能做成三角形框架的是(
???)
A.5cm,7cm,10cm??
??????????????B.5cm,7cm,13cm
C.7cm,10cm,13cm????????????????D.5cm,10cm,13cm
4、已知等腰三角形的两边长是4和10,则它的周长是(????
)
A.18????????
B.24???????????
C.18或24????????
D.14
5、若三角形的两边长分别为3和5,则其周长l的取值范围是(???
).
A.6<l<15????????????????????B.6<l<16
C.11<l<13???????????????????
D.10<l<16
6、从长度分别为10cm、20cm、30cm、40cm的四根木条中,任取三根可组成三角形的个数是(???
).
A.1个????????B.2个???????????
C.3个?????????D.4个
7、下列说法正确的是(
)
A.所有的等腰三角形都是锐角三角形
B.等边三角形属于等腰三角形
C.不存在既是钝角三角形又是等腰三角形的三角形
D.一个三角形里有两个锐角,则一定是锐角三角形
8、如图,已知△ABC中,AB=3,AC=5,BC=7,在△ABC所在平面内一条直线,将△ABC分割成两个三角形,使其中有一个边长为3的等腰三角形,则这样的直线最多可画( )
A.2条??????
B.3条??????
C.4条??????
D.5条
二、填空题
9、如图所示,顶点是A、B、C的三角形,记作______,读作______.其中,顶点A所对的边______还可用______表示;顶点B所对的边______还可用______表示;顶点C所对的边______还可用______表示.
??????????????
10、已知有两边相等的三角形的两边长分别为6
cm,4
cm,则该三角形的周长是 _________
11、边长为整数并且最大边长是5的三角形共有 个.?
12、由
“连接两点的线中,线段最短”这一性质可以得到三角形的三边有这样的性质______________________________.由它还可推出:三角形两边的差____________.
13、如图,在⊿ABC中,BC边上有n个点(包括B,C两点),则图中共有?????
个三角形.
?
△ABC的周长是12cm,边长分别为a
,b
,c
,且
a=b+1,b=c+1,则a=????
cm
,b=?????
cm
,c=?????
cm.
三、解答题
15、判断下列所给的三条线段能否围成三角形?
(1)5,5,a(0(2)a+1,a+2,a+3;
(3)三条线段的长度之比为2∶3∶5.
16、已知a,b,c是△ABC的三边,a,b满足|a-4|+(b-2)2=0,c为奇数,求△ABC的周长.
17、已知a,b,c为△ABC的三边长,化简|a+b+c|-|a-b-c|-|a-b+c|-|a+b-c|.
18、如图,用钉子把木棒AB,BC和CD连接起来,用橡皮筋把A,D两端连接起来,设橡皮筋AD的长是x
cm.
(1)若AB=5
cm,CD=3
cm,BC=11
cm,求x的最大值和最小值.
(2)在(1)的条件下要围成一个四边形,你能求出橡皮筋长x的取值范围吗?
19、小红用长度为10
cm,45
cm和50
cm的三根木条钉一个三角形,若将50
cm的木条截去一部分后,就怎么也钉不成一个三角形.
(1)最长的木条至少截去了多少厘米?
(2)如果最长的木条截去了25
cm,你通过怎样的截一根木条的方法钉成一个小三角形?
20、用一条长为35
cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的3倍,那么各边的长是多少?
(2)能围成有一边的长为1
cm的等腰三角形吗?为什么?
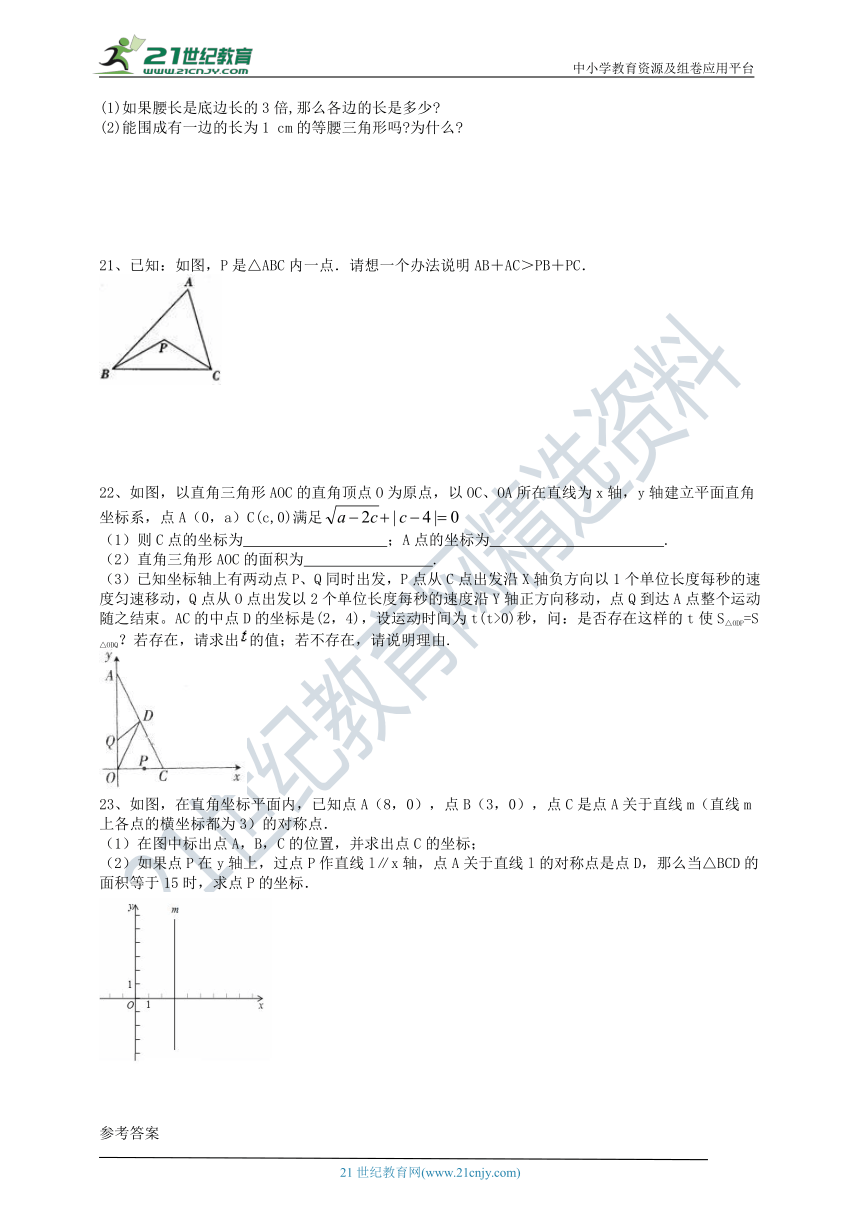
21、已知:如图,P是△ABC内一点.请想一个办法说明AB+AC>PB+PC.
22、如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴,y轴建立平面直角坐标系,点A(0,a)C(c,0)满足
(1)则C点的坐标为?????????
;A点的坐标为???????????
.
(2)直角三角形AOC的面积为????????
.
(3)已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿X轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿Y轴正方向移动,点Q到达A点整个运动随之结束。AC的中点D的坐标是(2,4),设运动时间为t(t>0)秒,问:是否存在这样的t使S△ODP=S△ODQ?若存在,请求出的值;若不存在,请说明理由.
23、如图,在直角坐标平面内,已知点A(8,0),点B(3,0),点C是点A关于直线m(直线m上各点的横坐标都为3)的对称点.
(1)在图中标出点A,B,C的位置,并求出点C的坐标;
(2)如果点P在y轴上,过点P作直线l∥x轴,点A关于直线l的对称点是点D,那么当△BCD的面积等于15时,求点P的坐标.
参考答案
一、选择题
1、B
2、D
3、B、
4、B???
5、D
6、D
7、B
8、C【解答】解:如图所示,当CA=CF=3,BC=BD=3,BC=CE=3,BG=CG,都能得到符合题意的等腰三角形.
二、填空题
9、△ABC,三角形ABC,BC,a;AC,b;AB,c
10、16
cm或14
cm .?
11、9
12、三角形两边之和大于第三边,小于第三边.
13、
14、5,4,3?
三、解答题
15、解:(1)∵0a,因而能构成三角形.
(2)当a=0时,a+1+a+2=2a+3=3,因而不能组成三角形.
(3)∵三条线段之比为2∶3∶5,∴设三条线段为2k,3k,5k,
∵2k+3k=5k,因而不能组成三角形.
16、解:∵|a-4|+(b-2)2=0,
∴a-4=0且b-2=0,
∴a=4,b=2,∴2∵c为奇数,∴c=3或5,
∴△ABC的周长为4+2+3=9或4+2+5=11.
18、解:(1)最大值应该是所有其他三条线段的和,即最大值是5+3+11=19(cm);
最小值是用最大的线段的长减去其他两条相对较短的线段的长,即最小值是11-3-5=3(cm).
(2)由(1)中的最大值和最小值可得要围成一个四边形,橡皮筋长x的取值范围为3
cmcm.
19、解:(1)∵已知两根木条的长为10
cm,45
cm,
设第三根木条长为x
cm,
∴45-10∵50-35=15,
∴最长的木条至少截去了15
cm.
(2)∵50-25=25,25+10<45,
∴将长45
cm的木条截去大于10
cm而小于30
cm的一部分,这根木条与其他两根木条可钉成一个小三角形.
20、解:(1)设底边长为x
cm,则腰长为3x
cm.
x+3x+3x=35,解得x=5.
故底边长为5
cm,腰长为15
cm.
(2)能.
当该边为腰长时,底边为35-1×2=33,33>2,所以不存在.
当该边为底边时,腰长为(35-1)÷2=17,符合条件,所以能.
故能围成有一边的长为1
cm的等腰三角形,腰长为17
cm.
21、提示:延长BP交AC于D.
∵在△ABD中,AB+AD>BD=BP+PD,①
在△DPC中,DP+DC>PC,②
由①、②,
∴AB+(AD+DC)+DP>BP+PC+DP.
即AB+AC>PB+PC.
22、解:(1)(4,0);(0,8)
????(2)16
????(3)存在.由条件可知P点从C点运动到O点的时间为4秒,Q点从O点运动到A点的时间为4秒,
当0<t≦4时,点q在线段AO上,点P在线段OC上,
即,,,,
∴8-2t=2t?
∴t=2.
23、解:(1)三个点位置标注正确
点C的坐标为(﹣2,0);
(2)如图,
由题意知S△BCD=BC?AD=15,BC=5,∴AD=6,则OP=3
∴点P的坐标为(0,3)或(0,﹣3)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
11.1.1三角形课时达标
选择题
1、三角形是(??
)
A.连接任意三个角组成的图形
B.由不在同一条直线上的三条线段首尾顺次相接所组成的图形
C.由三条线段组成的图形
D.以上说法均不对
2、如图所示,其中三角形的个数是( )
A.2个????
B.3个????
C.4个????
D.5个
3、下列长度的三根木棒首尾相接,不能做成三角形框架的是(
???)
A.5cm,7cm,10cm??
??????????????B.5cm,7cm,13cm
C.7cm,10cm,13cm????????????????D.5cm,10cm,13cm
4、已知等腰三角形的两边长是4和10,则它的周长是(????
)
A.18????????
B.24???????????
C.18或24????????
D.14
5、若三角形的两边长分别为3和5,则其周长l的取值范围是(???
).
A.6<l<15????????????????????B.6<l<16
C.11<l<13???????????????????
D.10<l<16
6、从长度分别为10cm、20cm、30cm、40cm的四根木条中,任取三根可组成三角形的个数是(???
).
A.1个????????B.2个???????????
C.3个?????????D.4个
7、下列说法正确的是(
)
A.所有的等腰三角形都是锐角三角形
B.等边三角形属于等腰三角形
C.不存在既是钝角三角形又是等腰三角形的三角形
D.一个三角形里有两个锐角,则一定是锐角三角形
8、如图,已知△ABC中,AB=3,AC=5,BC=7,在△ABC所在平面内一条直线,将△ABC分割成两个三角形,使其中有一个边长为3的等腰三角形,则这样的直线最多可画( )
A.2条??????
B.3条??????
C.4条??????
D.5条
二、填空题
9、如图所示,顶点是A、B、C的三角形,记作______,读作______.其中,顶点A所对的边______还可用______表示;顶点B所对的边______还可用______表示;顶点C所对的边______还可用______表示.
??????????????
10、已知有两边相等的三角形的两边长分别为6
cm,4
cm,则该三角形的周长是 _________
11、边长为整数并且最大边长是5的三角形共有 个.?
12、由
“连接两点的线中,线段最短”这一性质可以得到三角形的三边有这样的性质______________________________.由它还可推出:三角形两边的差____________.
13、如图,在⊿ABC中,BC边上有n个点(包括B,C两点),则图中共有?????
个三角形.
?
△ABC的周长是12cm,边长分别为a
,b
,c
,且
a=b+1,b=c+1,则a=????
cm
,b=?????
cm
,c=?????
cm.
三、解答题
15、判断下列所给的三条线段能否围成三角形?
(1)5,5,a(0
(3)三条线段的长度之比为2∶3∶5.
16、已知a,b,c是△ABC的三边,a,b满足|a-4|+(b-2)2=0,c为奇数,求△ABC的周长.
17、已知a,b,c为△ABC的三边长,化简|a+b+c|-|a-b-c|-|a-b+c|-|a+b-c|.
18、如图,用钉子把木棒AB,BC和CD连接起来,用橡皮筋把A,D两端连接起来,设橡皮筋AD的长是x
cm.
(1)若AB=5
cm,CD=3
cm,BC=11
cm,求x的最大值和最小值.
(2)在(1)的条件下要围成一个四边形,你能求出橡皮筋长x的取值范围吗?
19、小红用长度为10
cm,45
cm和50
cm的三根木条钉一个三角形,若将50
cm的木条截去一部分后,就怎么也钉不成一个三角形.
(1)最长的木条至少截去了多少厘米?
(2)如果最长的木条截去了25
cm,你通过怎样的截一根木条的方法钉成一个小三角形?
20、用一条长为35
cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的3倍,那么各边的长是多少?
(2)能围成有一边的长为1
cm的等腰三角形吗?为什么?
21、已知:如图,P是△ABC内一点.请想一个办法说明AB+AC>PB+PC.
22、如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴,y轴建立平面直角坐标系,点A(0,a)C(c,0)满足
(1)则C点的坐标为?????????
;A点的坐标为???????????
.
(2)直角三角形AOC的面积为????????
.
(3)已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿X轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿Y轴正方向移动,点Q到达A点整个运动随之结束。AC的中点D的坐标是(2,4),设运动时间为t(t>0)秒,问:是否存在这样的t使S△ODP=S△ODQ?若存在,请求出的值;若不存在,请说明理由.
23、如图,在直角坐标平面内,已知点A(8,0),点B(3,0),点C是点A关于直线m(直线m上各点的横坐标都为3)的对称点.
(1)在图中标出点A,B,C的位置,并求出点C的坐标;
(2)如果点P在y轴上,过点P作直线l∥x轴,点A关于直线l的对称点是点D,那么当△BCD的面积等于15时,求点P的坐标.
参考答案
一、选择题
1、B
2、D
3、B、
4、B???
5、D
6、D
7、B
8、C【解答】解:如图所示,当CA=CF=3,BC=BD=3,BC=CE=3,BG=CG,都能得到符合题意的等腰三角形.
二、填空题
9、△ABC,三角形ABC,BC,a;AC,b;AB,c
10、16
cm或14
cm .?
11、9
12、三角形两边之和大于第三边,小于第三边.
13、
14、5,4,3?
三、解答题
15、解:(1)∵0
(2)当a=0时,a+1+a+2=2a+3=3,因而不能组成三角形.
(3)∵三条线段之比为2∶3∶5,∴设三条线段为2k,3k,5k,
∵2k+3k=5k,因而不能组成三角形.
16、解:∵|a-4|+(b-2)2=0,
∴a-4=0且b-2=0,
∴a=4,b=2,∴2
∴△ABC的周长为4+2+3=9或4+2+5=11.
18、解:(1)最大值应该是所有其他三条线段的和,即最大值是5+3+11=19(cm);
最小值是用最大的线段的长减去其他两条相对较短的线段的长,即最小值是11-3-5=3(cm).
(2)由(1)中的最大值和最小值可得要围成一个四边形,橡皮筋长x的取值范围为3
cm
19、解:(1)∵已知两根木条的长为10
cm,45
cm,
设第三根木条长为x
cm,
∴45-10
∴最长的木条至少截去了15
cm.
(2)∵50-25=25,25+10<45,
∴将长45
cm的木条截去大于10
cm而小于30
cm的一部分,这根木条与其他两根木条可钉成一个小三角形.
20、解:(1)设底边长为x
cm,则腰长为3x
cm.
x+3x+3x=35,解得x=5.
故底边长为5
cm,腰长为15
cm.
(2)能.
当该边为腰长时,底边为35-1×2=33,33>2,所以不存在.
当该边为底边时,腰长为(35-1)÷2=17,符合条件,所以能.
故能围成有一边的长为1
cm的等腰三角形,腰长为17
cm.
21、提示:延长BP交AC于D.
∵在△ABD中,AB+AD>BD=BP+PD,①
在△DPC中,DP+DC>PC,②
由①、②,
∴AB+(AD+DC)+DP>BP+PC+DP.
即AB+AC>PB+PC.
22、解:(1)(4,0);(0,8)
????(2)16
????(3)存在.由条件可知P点从C点运动到O点的时间为4秒,Q点从O点运动到A点的时间为4秒,
当0<t≦4时,点q在线段AO上,点P在线段OC上,
即,,,,
∴8-2t=2t?
∴t=2.
23、解:(1)三个点位置标注正确
点C的坐标为(﹣2,0);
(2)如图,
由题意知S△BCD=BC?AD=15,BC=5,∴AD=6,则OP=3
∴点P的坐标为(0,3)或(0,﹣3)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
