11.1.2 三角形的高、中线与角平分线课时达标(含答案)
文档属性
| 名称 | 11.1.2 三角形的高、中线与角平分线课时达标(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-21 14:47:59 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
11.1.2三角形的高、中线与角平分线课时达标
一、选择题
1、下列说法错误的是(
)
A.锐角三角形的三条高、三条中线、三条角平分线分别交于一点
B.钝角三角形有两条高在三角形的外部
C.直角三角形只有一条高
D.任意三角形都有三条高、三条中线、三条角平分线
2、三角形的角平分线、中线和高(??
)???????
A.都是射线???
B.都是直线
C.都是线段????
D.都在三角形内
3、三角形的下列线段中能将三角形的面积分成相等两部分的是(
)
A.中线????????
??B.角平分线
C.高???????????
D.三等分线
4、若一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是(???
)
A.锐角三角形??????
B.钝角三角形??
C.直角三角形??
D.以上都
不对
5、下图中,正确画出△ABC的
AC边上的高的是
(???
)
A.???????
B.?????
?
C.??????
D.
6、如图所示,∠1=∠2,∠3=∠4,下列结论中错误的是(??
)
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3=∠ACB
D.CE是△ABC的角平分线
7、已知在ΔABC中,AB=AC,周长为24,AC边上的中线BD把ΔABC分成周长差为6的两个三角形,则
ΔABC各边的长分别变为______。
A.10、10、4???????
B.6、6、12???????
C.4、5、10??????
D.以上都不对
8、如图,已知BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是( )
A.2???
B.3???
C.6???
D.不能确定
9、如图在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点,且△ABC的面积是4,
则△BEF的面积是( ??)
A.1?
????
?B.
2??????
?
C.3????
?D.3.5
二、填空题
10、已知:如图,试回答下列问题:
(1)图中有______个三角形,它们分别是______________________________________.
(2)以线段AD为公共边的三角形是_________________________________________.
(3)线段CE所在的三角形是______,CE边所对的角是________________________.
(4)△ABC、△ACD、△ADE这三个三角形的面积之比等于______∶______∶______.
11、已知如图所示AD、AE分别是△ABC的中线、高,且AB=5cm,AC=3cm,则△ABD与△ACD的周长之差为?
??,△ABD与△ACD的面积关系为?
?
.
12、在△ABC中,CM是AB边上的中线,已知BC﹣AC=8cm,且△MBC的周长为30cm,则△AMC的周长为 ??
cm.
13、如图,在△ABC中,AD是边BC上的中线,在△ABD中,BE是边AD上的中线.若△ABC的面积是24,则△ABE的面积是 .?
14、如图,在△ABC中,E是底边BC上一点,且满足EC=2BE,BD是AC边上的中线,若S△ABC=15,则S△ADF-S△BEF=________.
三、解答题
15、如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
(1)画出△A′B′C′;
(2)画出AB边上的中线CD和高线CE;(利用网格点和直尺画图)
(3)△BCD的面积为 .?
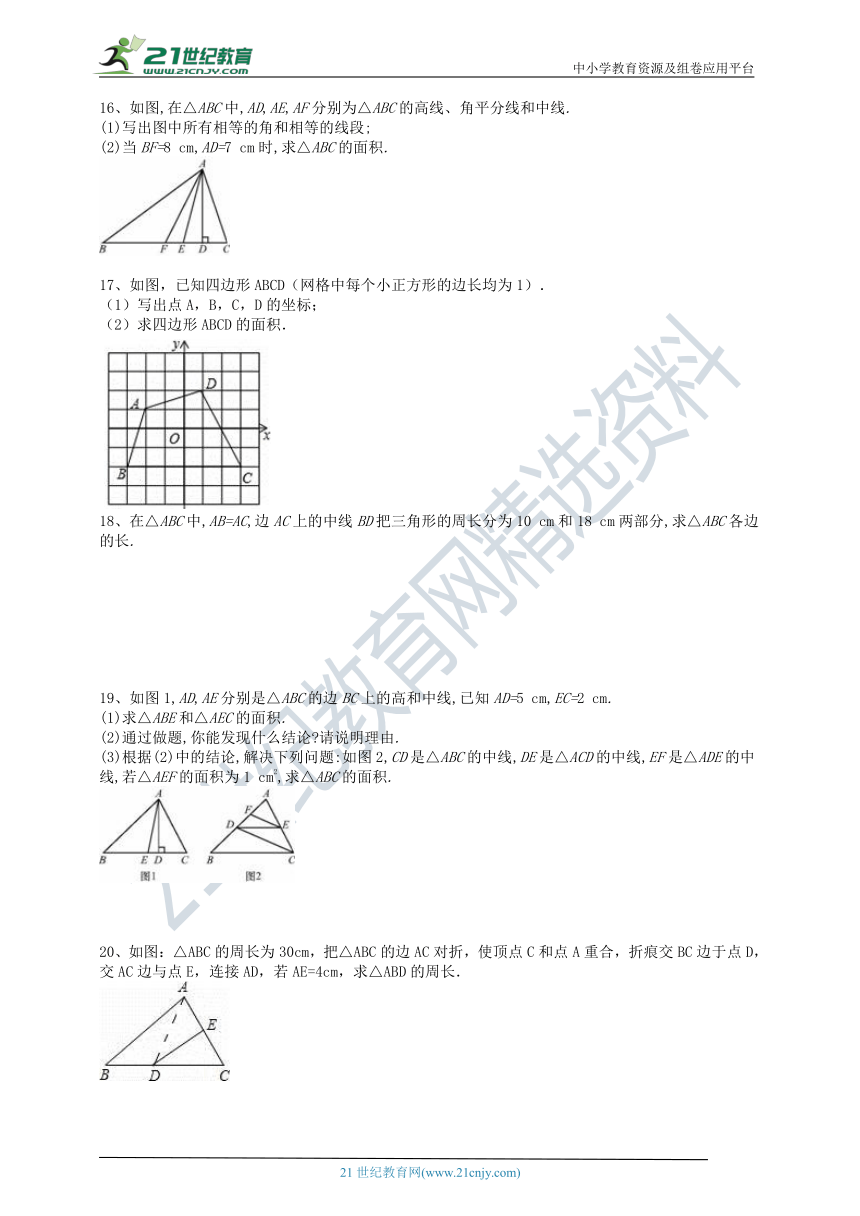
16、如图,在△ABC中,AD,AE,AF分别为△ABC的高线、角平分线和中线.
(1)写出图中所有相等的角和相等的线段;
(2)当BF=8
cm,AD=7
cm时,求△ABC的面积.
17、如图,已知四边形ABCD(网格中每个小正方形的边长均为1).
(1)写出点A,B,C,D的坐标;
(2)求四边形ABCD的面积.
18、在△ABC中,AB=AC,边AC上的中线BD把三角形的周长分为10
cm和18
cm两部分,求△ABC各边的长.
19、如图1,AD,AE分别是△ABC的边BC上的高和中线,已知AD=5
cm,EC=2
cm.
(1)求△ABE和△AEC的面积.
(2)通过做题,你能发现什么结论?请说明理由.
(3)根据(2)中的结论,解决下列问题:如图2,CD是△ABC的中线,DE是△ACD的中线,EF是△ADE的中线,若△AEF的面积为1
cm2,求△ABC的面积.
20、如图:△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边与点E,连接AD,若AE=4cm,求△ABD的周长.
21、已知△ABC的面积是60,请完成下列问题:
(1)如图1,若AD是△ABC的BC边上的中线,则△ABD的面积_______△ACD的面积(填“>”“<”或“=”)
(2)如图2,若CD、BE分别是△ABC的AB、AC边上的中线,求四边形ADOE的面积可以用如下方法:连接AO,由AD=DB得:S△ADO=S△BDO,同理:S△CEO=S△AEO,设S△ADO=x,S△CEO=y,则S△BDO=x,S△AEO=y由题意得:S△ABE=S△ABC=30,S△ADC=S△ABC=30,可列方程组为:,解得_______,通过解这个方程组可得四边形ADOE的面积为_______.
(3)如图3,AD:DB=1:3,CE:AE=1:2,请你计算四边形ADOE的面积,并说明理由.
参考答案
一、选择题
1、C
2、C?
3、A
4、C
5、C
6、D
7、A?
8、A
9、A
二、填空题
10、(1)六,△ABC、△ABD、△ABE、△ACD、△ACE、△ADE.
(2)△ABD、△ACD、△ADE.
(3)△ACE,∠CAE.
(4)BC:CD:DE.
11、2cm
相等,
12、22???
13、6
14、
三、解答题
15、(1)
(2)
略??
(3)
4??
16、解:(1)∵AE是△ABC的角平分线,∴∠BAE=∠CAE.
∵AD是△ABC的高,∴∠ADB=∠ADC=90°.
∵AF是△ABC的中线,∴BF=CF.
图中所有相等的角和相等的线段为∠BAE=∠CAE,∠ADB=∠ADC=90°,BF=CF.
(2)∵BF=CF,BF=8
cm,AD=7
cm,∴BC=2BF=2×8=16
cm,
∴S△ABC=BC·AD=×16
cm×7
cm=56
cm2.
答:△ABC的面积是56
cm2.
17、解:(1)由图象可知A(﹣2,1),B(﹣3,﹣2),C(3,﹣2),D(1,2);
(2)S四边形ABCD=S△ABE+S△ADF+S△CDG+S正方形AEGF
=×1×3+×1×3+×2×4+3×3=16??
18、解:设等腰三角形的腰长AB=AC=2x
cm,BC=y
cm,
∵BD是腰上的中线,∴AD=DC=x
cm.
若AB+AD=10
cm,则解得
此时组不成三角形,应舍去.
若AB+AD=18
cm,则解得
∴AB=AC=12
cm,BC=4
cm,
即△ABC各边的长分别为12
cm,12
cm和4
cm.
20、解:由图形和题意可知:AD=DC,AE=CE=4cm,则AB+BC=30﹣8=22(cm),
故△ABD的周长=AB+AD+BD=AB+CD+BC﹣CD=AB+BC,即可求出周长为22cm.
21、【考点】三角形的面积.
【分析】(1)根据等底等高的两个三角形面积相等知,三角形的中线把三角形的面积分为相等的两部分,所以S△ABD=S△ACD;
(2)根据三角形的中线能把三角形的面积平分,等高三角形的面积的比等于底的比,即可得到结果;
(3)连结AO,由AD:DB=1:3,得到S△ADO=S△BDO,同理可得S△CEO=S△AEO,设S△ADO=x,S△CEO=y,则S△BDO=3x,S△AEO=2y,由题意得列方程组即可得到结果.
【解答】解:(1)如图1,过A作AH⊥BC于H,
∵AD是△ABC的BC边上的中线,
∴BD=CD,
∴
∴S△ABD=S△ACD,
故答案为:=;
(2)解方程组得,
∴S△AOD=S△BOD=10,
∴S四边形ADOB=S△AOD+S△AOE=10+10=20,
故答案为:得,20;
(3)如图3,连结AO,
∵AD:DB=1:3,
∴S△ADO=S△BDO,
∵CE:AE=1:2,
∴S△CEO=S△AEO,
设S△ADO=x,S△CEO=y,则S△BDO=3x,S△AEO=2y,
由题意得:S△ABE=S△ABC=40,S△ADC=S△ABC=15,
可列方程组为:,
解得:,
∴S四边形ADOE=S△ADO+S△AEO=x+2
y=13.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
11.1.2三角形的高、中线与角平分线课时达标
一、选择题
1、下列说法错误的是(
)
A.锐角三角形的三条高、三条中线、三条角平分线分别交于一点
B.钝角三角形有两条高在三角形的外部
C.直角三角形只有一条高
D.任意三角形都有三条高、三条中线、三条角平分线
2、三角形的角平分线、中线和高(??
)???????
A.都是射线???
B.都是直线
C.都是线段????
D.都在三角形内
3、三角形的下列线段中能将三角形的面积分成相等两部分的是(
)
A.中线????????
??B.角平分线
C.高???????????
D.三等分线
4、若一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是(???
)
A.锐角三角形??????
B.钝角三角形??
C.直角三角形??
D.以上都
不对
5、下图中,正确画出△ABC的
AC边上的高的是
(???
)
A.???????
B.?????
?
C.??????
D.
6、如图所示,∠1=∠2,∠3=∠4,下列结论中错误的是(??
)
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3=∠ACB
D.CE是△ABC的角平分线
7、已知在ΔABC中,AB=AC,周长为24,AC边上的中线BD把ΔABC分成周长差为6的两个三角形,则
ΔABC各边的长分别变为______。
A.10、10、4???????
B.6、6、12???????
C.4、5、10??????
D.以上都不对
8、如图,已知BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是( )
A.2???
B.3???
C.6???
D.不能确定
9、如图在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点,且△ABC的面积是4,
则△BEF的面积是( ??)
A.1?
????
?B.
2??????
?
C.3????
?D.3.5
二、填空题
10、已知:如图,试回答下列问题:
(1)图中有______个三角形,它们分别是______________________________________.
(2)以线段AD为公共边的三角形是_________________________________________.
(3)线段CE所在的三角形是______,CE边所对的角是________________________.
(4)△ABC、△ACD、△ADE这三个三角形的面积之比等于______∶______∶______.
11、已知如图所示AD、AE分别是△ABC的中线、高,且AB=5cm,AC=3cm,则△ABD与△ACD的周长之差为?
??,△ABD与△ACD的面积关系为?
?
.
12、在△ABC中,CM是AB边上的中线,已知BC﹣AC=8cm,且△MBC的周长为30cm,则△AMC的周长为 ??
cm.
13、如图,在△ABC中,AD是边BC上的中线,在△ABD中,BE是边AD上的中线.若△ABC的面积是24,则△ABE的面积是 .?
14、如图,在△ABC中,E是底边BC上一点,且满足EC=2BE,BD是AC边上的中线,若S△ABC=15,则S△ADF-S△BEF=________.
三、解答题
15、如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
(1)画出△A′B′C′;
(2)画出AB边上的中线CD和高线CE;(利用网格点和直尺画图)
(3)△BCD的面积为 .?
16、如图,在△ABC中,AD,AE,AF分别为△ABC的高线、角平分线和中线.
(1)写出图中所有相等的角和相等的线段;
(2)当BF=8
cm,AD=7
cm时,求△ABC的面积.
17、如图,已知四边形ABCD(网格中每个小正方形的边长均为1).
(1)写出点A,B,C,D的坐标;
(2)求四边形ABCD的面积.
18、在△ABC中,AB=AC,边AC上的中线BD把三角形的周长分为10
cm和18
cm两部分,求△ABC各边的长.
19、如图1,AD,AE分别是△ABC的边BC上的高和中线,已知AD=5
cm,EC=2
cm.
(1)求△ABE和△AEC的面积.
(2)通过做题,你能发现什么结论?请说明理由.
(3)根据(2)中的结论,解决下列问题:如图2,CD是△ABC的中线,DE是△ACD的中线,EF是△ADE的中线,若△AEF的面积为1
cm2,求△ABC的面积.
20、如图:△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边与点E,连接AD,若AE=4cm,求△ABD的周长.
21、已知△ABC的面积是60,请完成下列问题:
(1)如图1,若AD是△ABC的BC边上的中线,则△ABD的面积_______△ACD的面积(填“>”“<”或“=”)
(2)如图2,若CD、BE分别是△ABC的AB、AC边上的中线,求四边形ADOE的面积可以用如下方法:连接AO,由AD=DB得:S△ADO=S△BDO,同理:S△CEO=S△AEO,设S△ADO=x,S△CEO=y,则S△BDO=x,S△AEO=y由题意得:S△ABE=S△ABC=30,S△ADC=S△ABC=30,可列方程组为:,解得_______,通过解这个方程组可得四边形ADOE的面积为_______.
(3)如图3,AD:DB=1:3,CE:AE=1:2,请你计算四边形ADOE的面积,并说明理由.
参考答案
一、选择题
1、C
2、C?
3、A
4、C
5、C
6、D
7、A?
8、A
9、A
二、填空题
10、(1)六,△ABC、△ABD、△ABE、△ACD、△ACE、△ADE.
(2)△ABD、△ACD、△ADE.
(3)△ACE,∠CAE.
(4)BC:CD:DE.
11、2cm
相等,
12、22???
13、6
14、
三、解答题
15、(1)
(2)
略??
(3)
4??
16、解:(1)∵AE是△ABC的角平分线,∴∠BAE=∠CAE.
∵AD是△ABC的高,∴∠ADB=∠ADC=90°.
∵AF是△ABC的中线,∴BF=CF.
图中所有相等的角和相等的线段为∠BAE=∠CAE,∠ADB=∠ADC=90°,BF=CF.
(2)∵BF=CF,BF=8
cm,AD=7
cm,∴BC=2BF=2×8=16
cm,
∴S△ABC=BC·AD=×16
cm×7
cm=56
cm2.
答:△ABC的面积是56
cm2.
17、解:(1)由图象可知A(﹣2,1),B(﹣3,﹣2),C(3,﹣2),D(1,2);
(2)S四边形ABCD=S△ABE+S△ADF+S△CDG+S正方形AEGF
=×1×3+×1×3+×2×4+3×3=16??
18、解:设等腰三角形的腰长AB=AC=2x
cm,BC=y
cm,
∵BD是腰上的中线,∴AD=DC=x
cm.
若AB+AD=10
cm,则解得
此时组不成三角形,应舍去.
若AB+AD=18
cm,则解得
∴AB=AC=12
cm,BC=4
cm,
即△ABC各边的长分别为12
cm,12
cm和4
cm.
20、解:由图形和题意可知:AD=DC,AE=CE=4cm,则AB+BC=30﹣8=22(cm),
故△ABD的周长=AB+AD+BD=AB+CD+BC﹣CD=AB+BC,即可求出周长为22cm.
21、【考点】三角形的面积.
【分析】(1)根据等底等高的两个三角形面积相等知,三角形的中线把三角形的面积分为相等的两部分,所以S△ABD=S△ACD;
(2)根据三角形的中线能把三角形的面积平分,等高三角形的面积的比等于底的比,即可得到结果;
(3)连结AO,由AD:DB=1:3,得到S△ADO=S△BDO,同理可得S△CEO=S△AEO,设S△ADO=x,S△CEO=y,则S△BDO=3x,S△AEO=2y,由题意得列方程组即可得到结果.
【解答】解:(1)如图1,过A作AH⊥BC于H,
∵AD是△ABC的BC边上的中线,
∴BD=CD,
∴
∴S△ABD=S△ACD,
故答案为:=;
(2)解方程组得,
∴S△AOD=S△BOD=10,
∴S四边形ADOB=S△AOD+S△AOE=10+10=20,
故答案为:得,20;
(3)如图3,连结AO,
∵AD:DB=1:3,
∴S△ADO=S△BDO,
∵CE:AE=1:2,
∴S△CEO=S△AEO,
设S△ADO=x,S△CEO=y,则S△BDO=3x,S△AEO=2y,
由题意得:S△ABE=S△ABC=40,S△ADC=S△ABC=15,
可列方程组为:,
解得:,
∴S四边形ADOE=S△ADO+S△AEO=x+2
y=13.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
