第十二章等腰三角形课件
图片预览

文档简介
本课件是八年级数学上册第十二章《轴对称》的总第七课时——“等腰三角形的性质”的一些片段。
采用office 2003制作的PPT课件,插入了《几何画板5.0版》(已经打包携带)。由于2003版本的原因,链接几何画板页面时,会弹出“可能有病毒”提示,这是“宏”的安全级别造成的,不是真有病毒,放心操作“确定”就是。若想退出几何画板页面,可以直接关闭此页面,也可以点击下面任务栏上PPT页面继续操作。
本节利用课件的亮点一是对折三角形,二是“三线合一”,均利用几何画板解决了。在画板中,你可以随意拖动图形,实现对折;随意调整三角形形状,从一般三角形到等腰三角形的过程中,清晰的看到三线逐渐重合。
本节的另一个难点是把文字语言改写为符号语言。在本课件中的“思维发散”模块中,巧妙避开了线性结构,“兵分三路”用三种不同方法证明三线合一,设置了三个按钮,分别点击,进入不同模块,都能返回“思维发散”模块,最后单击空白,则进入小结。在小结里以表格形式再次突出了符号语言。
画面的风格朴素清雅,不失美感。贯穿始终的蝴蝶,正是轴对称图形,还有引起人们广泛兴趣的“蝴蝶定理”,曾是著名的几何难题,它的图形就是一只翩翩起舞的蝴蝶。所以蝴蝶充当了一个小小的配角,也为本课件增添了些许点缀。
片头和片尾不须点击,设置了自动播放,在婉转的音乐声中,于课前课后给师生们送来一点轻松、一点愉悦。(共9张PPT)
情景引入:
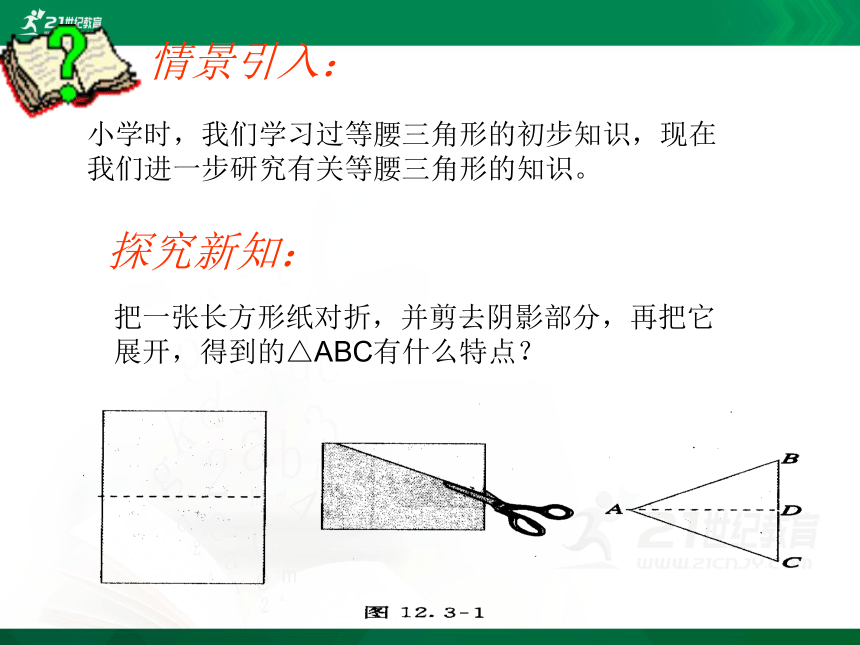
小学时,我们学习过等腰三角形的初步知识,现在我们进一步研究有关等腰三角形的知识。
探究新知:
把一张长方形纸对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特点?
思考
1 我们在上述过程中剪制出的三角形边有何关系?我们得到的三角形是什么三角形?
上面剪出的等腰三角形是轴对称图形吗 把剪出的三角形ABC沿折痕对折,找出重合的线段和角,你能发现等腰三角形的性质吗?
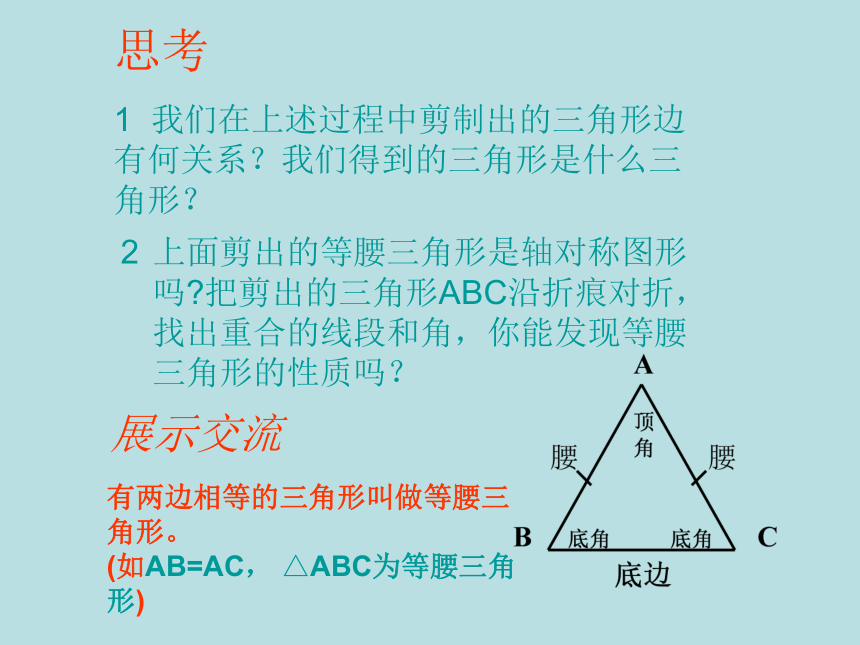
展示交流
有两边相等的三角形叫做等腰三角形。
(如AB=AC, △ABC为等腰三角形)
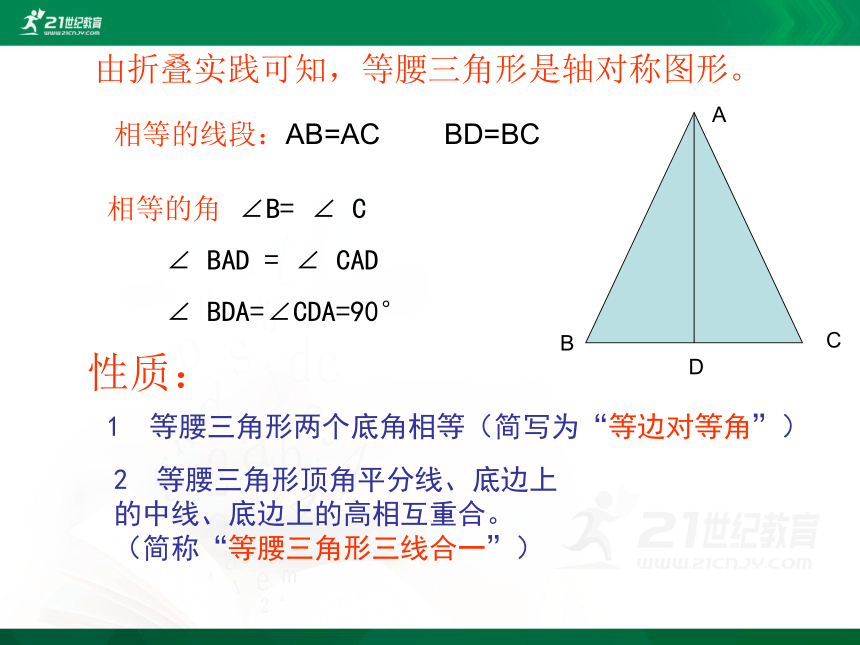
由折叠实践可知,等腰三角形是轴对称图形。
相等的线段:AB=AC BD=BC
相等的角 ∠B= ∠ C
∠ BAD = ∠ CAD
∠ BDA=∠CDA=90°
性质:
1 等腰三角形两个底角相等(简写为“等边对等角”)
2 等腰三角形顶角平分线、底边上的中线、底边上的高相互重合。(简称“等腰三角形三线合一”)
A
B
C
D
从上面的操作过程获得启发,我们可以通过作辅助线利用全等三角形的知识来证明这些性质。
A
B
C
D
AB=AC
BD=CD
AD=AD
∴ BAD≌△CAD
∠B= ∠ C
∵
用类似的方法我们还可以证明等腰三角形的其他性质:
如图: △ ABC中,AB=AC
用理论知识,证明出性质1的结论:等腰三角形的两个底角相等
学生展示自己的证明方法,以小组为合作单位,师生和谐交流,达成共识
作底边中线AD
例题讲解
如图在△ABC中,AB=AC,点D在AC上,
且 BD=BC=AD求△ABC各角的度数.
解:∵AB=AC, BD=BC=AD
∴∠ABC=∠C=∠BDC
∠A=∠ABD
设∠A=x,则
∠BDC=∠A+∠ABD=2x
从而∠ABC=∠C=∠BDC=2x
于是在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180
解得x=36
在△ABC中,∠A=36 ° ∠ABC=∠C=72 °
巩固训练
1、等腰三角形的一个角是40度,它的另外两个角的度数是多少呢?
2、等腰三角形的一个角是100度,它的另外两个角的度数是多少呢?
3、等腰三角形的底边长为7cm,一腰长的中线周长分为两部分其差为3cm,则等腰三角形的腰为多少?
4、等腰三角形两边分别为35厘米和22厘米, 则它的
第三边长为( )
A.35cm B.22cm C.35cm或22cm D.15cm
补偿提高:
. 1 等腰三角形的顶角等于一个底角的4倍时, 则顶角为____度.
3 如图(3), 已知:点D,E在△ABC的边BC上,AB=AC,AD=AE.
求证:BD=CE
2 如图(2) 在△ABC中, AB=AC, CD⊥AB于D, 则下列判断正确的是
A.∠A=∠B B.∠A=∠ACD C.∠A=∠DCB D.∠A=2∠BCD
A
B
C
D
图(2)
A
B
C
D
E
图(3)
说一说
通过本节课的学习,你们都有哪些收获?
采用office 2003制作的PPT课件,插入了《几何画板5.0版》(已经打包携带)。由于2003版本的原因,链接几何画板页面时,会弹出“可能有病毒”提示,这是“宏”的安全级别造成的,不是真有病毒,放心操作“确定”就是。若想退出几何画板页面,可以直接关闭此页面,也可以点击下面任务栏上PPT页面继续操作。
本节利用课件的亮点一是对折三角形,二是“三线合一”,均利用几何画板解决了。在画板中,你可以随意拖动图形,实现对折;随意调整三角形形状,从一般三角形到等腰三角形的过程中,清晰的看到三线逐渐重合。
本节的另一个难点是把文字语言改写为符号语言。在本课件中的“思维发散”模块中,巧妙避开了线性结构,“兵分三路”用三种不同方法证明三线合一,设置了三个按钮,分别点击,进入不同模块,都能返回“思维发散”模块,最后单击空白,则进入小结。在小结里以表格形式再次突出了符号语言。
画面的风格朴素清雅,不失美感。贯穿始终的蝴蝶,正是轴对称图形,还有引起人们广泛兴趣的“蝴蝶定理”,曾是著名的几何难题,它的图形就是一只翩翩起舞的蝴蝶。所以蝴蝶充当了一个小小的配角,也为本课件增添了些许点缀。
片头和片尾不须点击,设置了自动播放,在婉转的音乐声中,于课前课后给师生们送来一点轻松、一点愉悦。(共9张PPT)
情景引入:
小学时,我们学习过等腰三角形的初步知识,现在我们进一步研究有关等腰三角形的知识。
探究新知:
把一张长方形纸对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特点?
思考
1 我们在上述过程中剪制出的三角形边有何关系?我们得到的三角形是什么三角形?
上面剪出的等腰三角形是轴对称图形吗 把剪出的三角形ABC沿折痕对折,找出重合的线段和角,你能发现等腰三角形的性质吗?
展示交流
有两边相等的三角形叫做等腰三角形。
(如AB=AC, △ABC为等腰三角形)
由折叠实践可知,等腰三角形是轴对称图形。
相等的线段:AB=AC BD=BC
相等的角 ∠B= ∠ C
∠ BAD = ∠ CAD
∠ BDA=∠CDA=90°
性质:
1 等腰三角形两个底角相等(简写为“等边对等角”)
2 等腰三角形顶角平分线、底边上的中线、底边上的高相互重合。(简称“等腰三角形三线合一”)
A
B
C
D
从上面的操作过程获得启发,我们可以通过作辅助线利用全等三角形的知识来证明这些性质。
A
B
C
D
AB=AC
BD=CD
AD=AD
∴ BAD≌△CAD
∠B= ∠ C
∵
用类似的方法我们还可以证明等腰三角形的其他性质:
如图: △ ABC中,AB=AC
用理论知识,证明出性质1的结论:等腰三角形的两个底角相等
学生展示自己的证明方法,以小组为合作单位,师生和谐交流,达成共识
作底边中线AD
例题讲解
如图在△ABC中,AB=AC,点D在AC上,
且 BD=BC=AD求△ABC各角的度数.
解:∵AB=AC, BD=BC=AD
∴∠ABC=∠C=∠BDC
∠A=∠ABD
设∠A=x,则
∠BDC=∠A+∠ABD=2x
从而∠ABC=∠C=∠BDC=2x
于是在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180
解得x=36
在△ABC中,∠A=36 ° ∠ABC=∠C=72 °
巩固训练
1、等腰三角形的一个角是40度,它的另外两个角的度数是多少呢?
2、等腰三角形的一个角是100度,它的另外两个角的度数是多少呢?
3、等腰三角形的底边长为7cm,一腰长的中线周长分为两部分其差为3cm,则等腰三角形的腰为多少?
4、等腰三角形两边分别为35厘米和22厘米, 则它的
第三边长为( )
A.35cm B.22cm C.35cm或22cm D.15cm
补偿提高:
. 1 等腰三角形的顶角等于一个底角的4倍时, 则顶角为____度.
3 如图(3), 已知:点D,E在△ABC的边BC上,AB=AC,AD=AE.
求证:BD=CE
2 如图(2) 在△ABC中, AB=AC, CD⊥AB于D, 则下列判断正确的是
A.∠A=∠B B.∠A=∠ACD C.∠A=∠DCB D.∠A=2∠BCD
A
B
C
D
图(2)
A
B
C
D
E
图(3)
说一说
通过本节课的学习,你们都有哪些收获?
