人教版数学八年级上册:11.3.2 多边形内角和(共20张PPT) 课件
文档属性
| 名称 | 人教版数学八年级上册:11.3.2 多边形内角和(共20张PPT) 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-21 17:03:18 | ||
图片预览







文档简介
(共20张PPT)
11.3.2
多边形的内角和
学习目标:
1、知道多边形的内角和定理。
2、运用多边形内角和进行有关计算。
从一个点引出的对角线的条数:
1
2
3
n-3
分割出的三角形的个数:
2
3
4
n-2
0
1
n边形从一个顶点出发的对角线条数为:
条(n≥3)
n边形共有对角线
条(n≥3)
(n-3)
自学指导:
阅读课本21页-22页内容,完成22页填空,并试做24页“练习”第1题。
画出任意一个四边形的一条对角线,都能将这个四边形分为两个三角形,这样,任意一个四边形的内角和,都等于________________,即360°。
四边形内角和为360°
两个三角形的内角和
自学检测
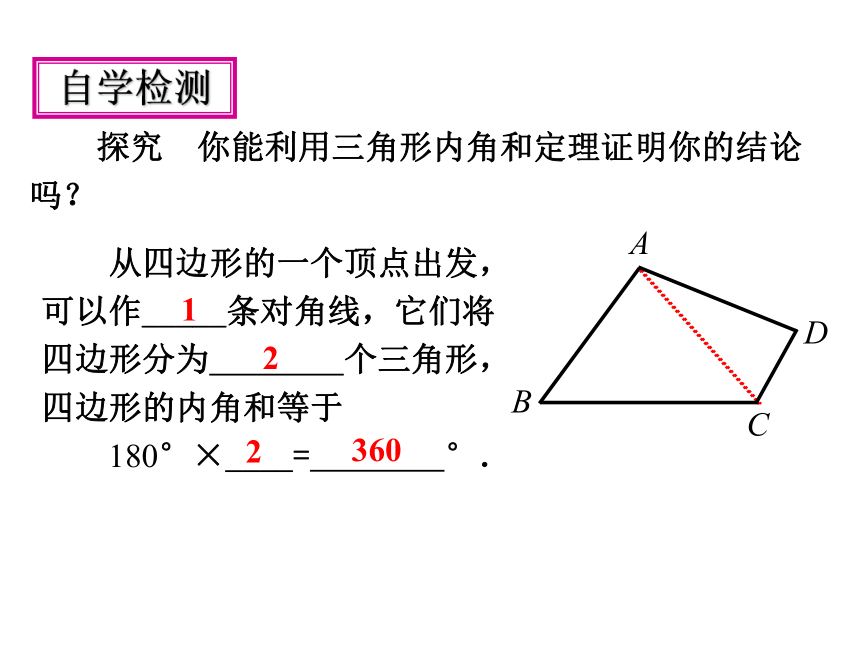
探究 你能利用三角形内角和定理证明你的结论
吗?
从四边形的一个顶点出发,
可以作_____条对角线,它们将
四边形分为 个三角形,
四边形的内角和等于
180°×____= °.
1
2
2
360
探究 类比前面的过程,你能探索五边形的内角和
吗?六边形呢?
如图,从五边形的一个顶点
出发,可以作 条对角线,它
们将五边形分为____个三角形,
五边形的内角和等于
180°× = °.
2
3
3
540
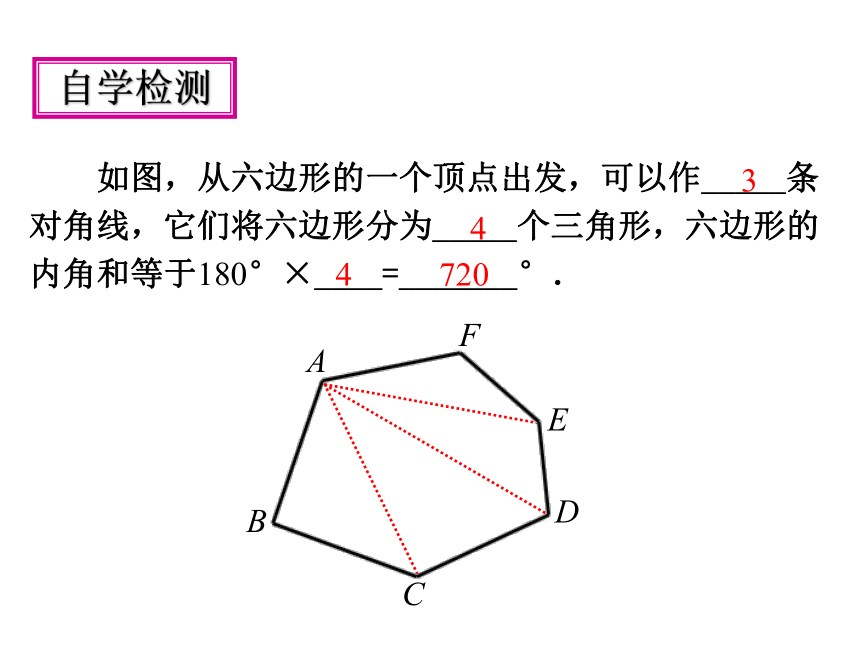
自学检测
如图,从六边形的一个顶点出发,可以作_____条
对角线,它们将六边形分为_____个三角形,六边形的
内角和等于180°×____=_______°.
3
4
4
720
C
自学检测
······
0
3
-3
=
4
-3
=
5
-3
=
6
-3
=
n
-3
1
2
3
3
-2
=
1
4
-2
=
2
5
-2
=
3
6
-2
=
4
n
-2
(
n
-2
)·180?
180?
360?
540?
720?
······
······
······
自学检测
—————
—————
———————
从n
边形的一个顶点出发,可以作_______条对角
线,它们将n
边形分为______个三角形,这_________
个三角形的内角和就是n
边形的内角和,所以,n
边形
的内角和等于___________.
思考 你能从四边形、五边形、六边形的内角和的
研究过程获得启发,发现多边形的内角和与边数的关系
吗?能证明你发现的结论吗?
自学检测
(n
-2)×180°
(n
-3)
(n
-2)
(n
-2)
幸
运
金
蛋
当堂检测
9边形的内角和是多少?
一个多边形的内角和为720度,则该多边形为几边形?
一个多边形的内角和为900度,则该多边形为几边形?
如果一个四边形的一组对角互补,那么另一组对角有什么关系?
十二边形的内角和是(
).
一个多边形当边数增加1时,它的内角和增加(
).
一个多边形的内角和是720?,则此多边形共有(
)个内角.
如果一个多边形的内角和是1440°,那么这是(
)边形.
在五边形ABCDE中,若∠A=∠D=90o,且
∠B:∠C:∠E=3:2:4,则∠C的度数为_______
1800?
180?
六
十
80o
当堂训练
6、求下列图形中x的值。
X=65
X=95
n边形的内角和:
(n
-
2)?180°
作业布置:
课本25页,第4题,第5题。
11.3.2
多边形的内角和
学习目标:
1、知道多边形的内角和定理。
2、运用多边形内角和进行有关计算。
从一个点引出的对角线的条数:
1
2
3
n-3
分割出的三角形的个数:
2
3
4
n-2
0
1
n边形从一个顶点出发的对角线条数为:
条(n≥3)
n边形共有对角线
条(n≥3)
(n-3)
自学指导:
阅读课本21页-22页内容,完成22页填空,并试做24页“练习”第1题。
画出任意一个四边形的一条对角线,都能将这个四边形分为两个三角形,这样,任意一个四边形的内角和,都等于________________,即360°。
四边形内角和为360°
两个三角形的内角和
自学检测
探究 你能利用三角形内角和定理证明你的结论
吗?
从四边形的一个顶点出发,
可以作_____条对角线,它们将
四边形分为 个三角形,
四边形的内角和等于
180°×____= °.
1
2
2
360
探究 类比前面的过程,你能探索五边形的内角和
吗?六边形呢?
如图,从五边形的一个顶点
出发,可以作 条对角线,它
们将五边形分为____个三角形,
五边形的内角和等于
180°× = °.
2
3
3
540
自学检测
如图,从六边形的一个顶点出发,可以作_____条
对角线,它们将六边形分为_____个三角形,六边形的
内角和等于180°×____=_______°.
3
4
4
720
C
自学检测
······
0
3
-3
=
4
-3
=
5
-3
=
6
-3
=
n
-3
1
2
3
3
-2
=
1
4
-2
=
2
5
-2
=
3
6
-2
=
4
n
-2
(
n
-2
)·180?
180?
360?
540?
720?
······
······
······
自学检测
—————
—————
———————
从n
边形的一个顶点出发,可以作_______条对角
线,它们将n
边形分为______个三角形,这_________
个三角形的内角和就是n
边形的内角和,所以,n
边形
的内角和等于___________.
思考 你能从四边形、五边形、六边形的内角和的
研究过程获得启发,发现多边形的内角和与边数的关系
吗?能证明你发现的结论吗?
自学检测
(n
-2)×180°
(n
-3)
(n
-2)
(n
-2)
幸
运
金
蛋
当堂检测
9边形的内角和是多少?
一个多边形的内角和为720度,则该多边形为几边形?
一个多边形的内角和为900度,则该多边形为几边形?
如果一个四边形的一组对角互补,那么另一组对角有什么关系?
十二边形的内角和是(
).
一个多边形当边数增加1时,它的内角和增加(
).
一个多边形的内角和是720?,则此多边形共有(
)个内角.
如果一个多边形的内角和是1440°,那么这是(
)边形.
在五边形ABCDE中,若∠A=∠D=90o,且
∠B:∠C:∠E=3:2:4,则∠C的度数为_______
1800?
180?
六
十
80o
当堂训练
6、求下列图形中x的值。
X=65
X=95
n边形的内角和:
(n
-
2)?180°
作业布置:
课本25页,第4题,第5题。
