2012届高考数学文科一轮复习精选课件(新人教a版):7.2 空间几何体的表面积与体积
文档属性
| 名称 | 2012届高考数学文科一轮复习精选课件(新人教a版):7.2 空间几何体的表面积与体积 |  | |
| 格式 | rar | ||
| 文件大小 | 816.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-06-15 18:39:10 | ||
图片预览





文档简介
(共26张PPT)
学案2 空间几何体的表面
积与体积
考点1
考点2
考点3
填填知学情
课内考点突破
规 律 探 究
考 纲 解 读
考 向 预 测
返回目录
考 纲 解 读
空间几何体的表面积与体积 了解球、棱柱、棱锥、台的表面积和体积的计算公式(不要求记忆公式).
简单的组合体的面积与体积的计算,以及平面图形的折叠问题是常考的内容,尤其是在解答题中,多涉及位置关系的证明,面积或体积的计算,着重考查学生识图,用图及空间想象能力,有时也与三视图结合考查.
考 向 预 测
返回目录
1.设直棱柱高为h,底面多边形的周长为c,则直棱柱侧面面积计算公式:S直棱柱侧= .即直棱柱的侧面积等于它的 .
2.设正n棱锥的底面边长为a,底面周长为c,斜高为h′,则正n棱锥的侧面积的计算公式:S正棱锥侧= ,即正棱锥的侧面积等于它的 .
ch
底面周长和高的乘积
nah′= ch′
底面的周长和斜高乘积的一半
返回目录
3.设棱台下底面边长为a,周长为c,上底面边长为a′,周长为c′,斜高为h′,则正n棱台的侧面积公式:S正棱台侧= .
4.棱柱、棱锥、棱台的表面积或全面积等于 .
5.半径为R的球的表面积公式:S球= ,即球面面积等于它的 .
大圆面积的四倍
n(a+a′)h′= (c+c′)h′
侧面积与底面积的和
4πR2
返回目录
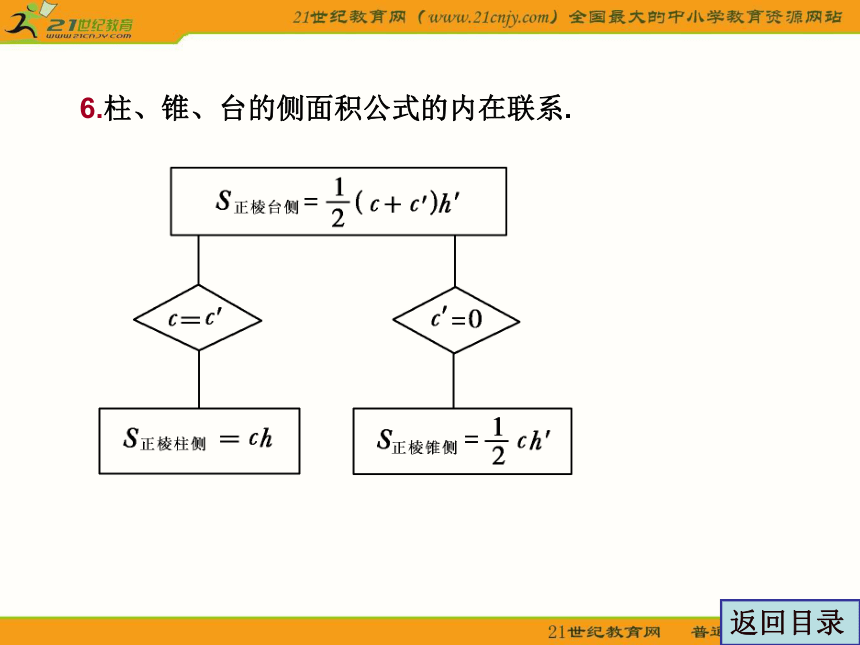
6.柱、锥、台的侧面积公式的内在联系.
返回目录
7.柱体(棱柱、圆柱)的体积等于它的 ,即V柱体= .底面半径是r,高是h的圆柱体的体积的计算公式是V圆柱= .
8.如果一个锥体(棱锥、圆锥)的底面积是S,高是h,那么它的体积是V锥体= .
如果圆锥的底面半径是r,高是h,则它的体积V圆锥= .
9.如果一个台体(棱台、圆台)的上、下底面的面积分别是S′,S,高是h,那么它的体积V台体= h(S+ +S′).
如果圆台的上、下底面的半径分别是r′,r,高是h,则它的体积是V圆台= πh(r′2+r′r+r2).
底面积S和高h的乘积
Sh
πr2h
Sh
πr2h
返回目录
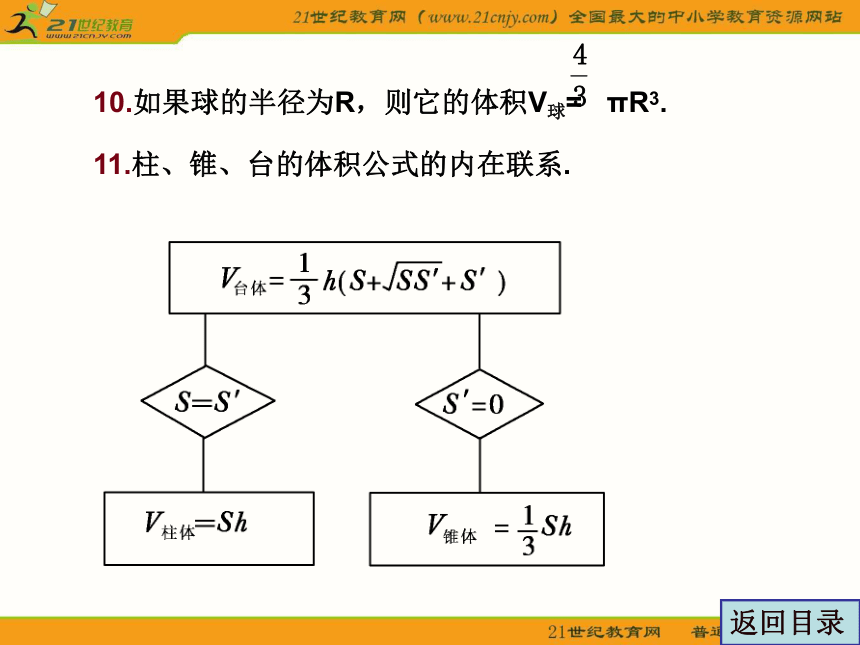
10.如果球的半径为R,则它的体积V球= πR3.
11.柱、锥、台的体积公式的内在联系.
返回目录
[2009年高考海南·宁夏卷]一个棱锥的三视图如图所示,则该棱锥的全面积(单位:cm2)为( )
A.48+12 B.48+24
C.36+12 D.36+24
考点1 几何体的表面积问题
返回目录
【解析】该几何体是一个底面为直角三角形的三棱锥,如图,SE=5,SD=4,AC=6 ,AB=BC=6,
∴S全=S△ABC+2S△SAB+S△ASC
= ×6×6+2× ×5×6+
×6 ×4=48+12 .
故应选A.
【分析】由三视图还原几何体,根据各面的特征分别求面积,再求表面积.
返回目录
(1)多面体的表面积是各个面的面积之和.
圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展为平面图形,其表面积为侧面积与底面积之和.
(2)组合体的表面积要注意重合部分的处理.
返回目录
[2010年高考安徽卷]一个几何体的三视图如图,该几何体的表面积为( )
A.280 B.292
C.360 D.372
返回目录
【解析】由三视图可知该几何是由下面一个长方体,上面一个长方体组合而成的几何体.
∵下面长方体的表面积为8×10×2+2×8×2+10×2×2=232,上面长方体的表面积为8×6×2+2×8×2+2×6×2=152,
又∵长方体表面积重叠一部分,
∴几何体的表面积为232+152-2×6×2=360.
故应选C.
返回目录
[2010年高考天津卷]一个几何体的三视图如图所示,则这个几何体的体积为 .
【分析】由三视图判断几何体的构成,根据所给数据求出有关量,并求体积.
考点2 几何体的体积
返回目录
【解析】该几何体是上面是底面边长为2的正四棱锥,下面是底面边长为1,高为2的正四棱柱的组合体,其体积为
V=1×1×2+ ×22×1= .
返回目录
(1)三棱锥体积的计算与等体积法
对于三棱锥的体积计算时,三棱锥的顶点和底面是相对的,可以变换顶点和底面,使体积容易计算.
(2)求空间几何体的体积除利用公式法外,还常用分割法、补体法、转化法等,它们是解决一些不规则几何体体积计算问题的常用方法.
返回目录
B.
C. 1 D.2
[2010年高考陕西卷]若某空间几何体的三视图如图所示,则该几何体的体积是( )
返回目录
【解析】由三视图可知,该空间几何体是底面为直角三角形的直三棱柱,三棱柱的底面直角三角形的直角边长分别为1和 ,三棱柱的高为 ,所以该几何体的体积V= ×1× × =1.
故应选C.
返回目录
[2010年高考辽宁卷]已知S,A,B,C是球O表面上的点,SA⊥平面ABC,AB⊥BC,SA=AB=1,BC= ,则球O的表面积等于( )
A.4π B.3π C.2π D.π
【分析】根据条件,确定球O的位置,并求出球半径.
考点3 球的表面积、体积
返回目录
【解析】如图所示,A,B,C三点在一小圆面上,
∵AB⊥BC,AC为斜边,
∴小圆的圆心为AC的中点D.
∵SA=AB=1,BC=2,
∴AC= ,AD= .
∵S,A,B,C都在球面上,取SC的中点O,则OD∥SA.
∵SA⊥平面ABC,∴OD⊥平面ABC,
∴O为球心,SO为半径.
∵SC= =2,∴SO=1,
∴球O的表面积为4π.
返回目录
本题考查球的几何性质及表面积公式,考查运算求解能力,考查数形结合、转化与化归思想,难度较大.
返回目录
在球心同侧有相距9 cm的两个平行截面,它们的面积分别为49π cm2和400π cm2.求球的表面积.
【解析】如图为球的轴截面,由球的截面性质知,AO1∥BO2,且O1,O2分别为两截面圆的圆心,则OO1⊥AO1,OO2⊥BO2,设球的半径为R.
返回目录
∵π·O2B2=49π,∴O2B=7(cm).
∵π·O1A2=400π,∴O1A=20(cm).
设OO1=x cm,则OO2=(x+9) cm.
在Rt△OO1A中,R2=x2+202.
在Rt△OO2B中,R2=(x+9)2+72,
∴x2+202=72+(x+9)2,
解得x=15,
∴R2=x2+202=252,∴R=25.
∴S球=4πR2=2 500π(cm2).
∴球的表面积为2 500π cm2.
返回目录
1.对于基本概念和能用公式直接求出棱柱、棱锥、棱台与球的表面积的问题,要结合它们的结构特点与平面几何知识来解决,这种题目难度不大.
2.要注意将空间问题转化为平面问题.
3.当给出的几何体比较复杂,有关的计算公式无法运用,或者虽然几何体并不复杂,但条件中的已知元素彼此离散时,我们可采用“割”、“补”的技巧,化复杂几何体为简单几何体(柱、锥、台),或化离散为集中,给解题提供便利.
返回目录
4.与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形 , 明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图 ,如球内切于正方体 ,切点为正方体各个面 的 中心,正方体的棱长等于球的直 径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线等于球的直径.球与旋转体的组合,通常作它们的轴截面进行解题,球与多面体的组合,通过多面体的一条侧棱和球心,或“切点”“接点”作出截面图.
返回目录
学案2 空间几何体的表面
积与体积
考点1
考点2
考点3
填填知学情
课内考点突破
规 律 探 究
考 纲 解 读
考 向 预 测
返回目录
考 纲 解 读
空间几何体的表面积与体积 了解球、棱柱、棱锥、台的表面积和体积的计算公式(不要求记忆公式).
简单的组合体的面积与体积的计算,以及平面图形的折叠问题是常考的内容,尤其是在解答题中,多涉及位置关系的证明,面积或体积的计算,着重考查学生识图,用图及空间想象能力,有时也与三视图结合考查.
考 向 预 测
返回目录
1.设直棱柱高为h,底面多边形的周长为c,则直棱柱侧面面积计算公式:S直棱柱侧= .即直棱柱的侧面积等于它的 .
2.设正n棱锥的底面边长为a,底面周长为c,斜高为h′,则正n棱锥的侧面积的计算公式:S正棱锥侧= ,即正棱锥的侧面积等于它的 .
ch
底面周长和高的乘积
nah′= ch′
底面的周长和斜高乘积的一半
返回目录
3.设棱台下底面边长为a,周长为c,上底面边长为a′,周长为c′,斜高为h′,则正n棱台的侧面积公式:S正棱台侧= .
4.棱柱、棱锥、棱台的表面积或全面积等于 .
5.半径为R的球的表面积公式:S球= ,即球面面积等于它的 .
大圆面积的四倍
n(a+a′)h′= (c+c′)h′
侧面积与底面积的和
4πR2
返回目录
6.柱、锥、台的侧面积公式的内在联系.
返回目录
7.柱体(棱柱、圆柱)的体积等于它的 ,即V柱体= .底面半径是r,高是h的圆柱体的体积的计算公式是V圆柱= .
8.如果一个锥体(棱锥、圆锥)的底面积是S,高是h,那么它的体积是V锥体= .
如果圆锥的底面半径是r,高是h,则它的体积V圆锥= .
9.如果一个台体(棱台、圆台)的上、下底面的面积分别是S′,S,高是h,那么它的体积V台体= h(S+ +S′).
如果圆台的上、下底面的半径分别是r′,r,高是h,则它的体积是V圆台= πh(r′2+r′r+r2).
底面积S和高h的乘积
Sh
πr2h
Sh
πr2h
返回目录
10.如果球的半径为R,则它的体积V球= πR3.
11.柱、锥、台的体积公式的内在联系.
返回目录
[2009年高考海南·宁夏卷]一个棱锥的三视图如图所示,则该棱锥的全面积(单位:cm2)为( )
A.48+12 B.48+24
C.36+12 D.36+24
考点1 几何体的表面积问题
返回目录
【解析】该几何体是一个底面为直角三角形的三棱锥,如图,SE=5,SD=4,AC=6 ,AB=BC=6,
∴S全=S△ABC+2S△SAB+S△ASC
= ×6×6+2× ×5×6+
×6 ×4=48+12 .
故应选A.
【分析】由三视图还原几何体,根据各面的特征分别求面积,再求表面积.
返回目录
(1)多面体的表面积是各个面的面积之和.
圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展为平面图形,其表面积为侧面积与底面积之和.
(2)组合体的表面积要注意重合部分的处理.
返回目录
[2010年高考安徽卷]一个几何体的三视图如图,该几何体的表面积为( )
A.280 B.292
C.360 D.372
返回目录
【解析】由三视图可知该几何是由下面一个长方体,上面一个长方体组合而成的几何体.
∵下面长方体的表面积为8×10×2+2×8×2+10×2×2=232,上面长方体的表面积为8×6×2+2×8×2+2×6×2=152,
又∵长方体表面积重叠一部分,
∴几何体的表面积为232+152-2×6×2=360.
故应选C.
返回目录
[2010年高考天津卷]一个几何体的三视图如图所示,则这个几何体的体积为 .
【分析】由三视图判断几何体的构成,根据所给数据求出有关量,并求体积.
考点2 几何体的体积
返回目录
【解析】该几何体是上面是底面边长为2的正四棱锥,下面是底面边长为1,高为2的正四棱柱的组合体,其体积为
V=1×1×2+ ×22×1= .
返回目录
(1)三棱锥体积的计算与等体积法
对于三棱锥的体积计算时,三棱锥的顶点和底面是相对的,可以变换顶点和底面,使体积容易计算.
(2)求空间几何体的体积除利用公式法外,还常用分割法、补体法、转化法等,它们是解决一些不规则几何体体积计算问题的常用方法.
返回目录
B.
C. 1 D.2
[2010年高考陕西卷]若某空间几何体的三视图如图所示,则该几何体的体积是( )
返回目录
【解析】由三视图可知,该空间几何体是底面为直角三角形的直三棱柱,三棱柱的底面直角三角形的直角边长分别为1和 ,三棱柱的高为 ,所以该几何体的体积V= ×1× × =1.
故应选C.
返回目录
[2010年高考辽宁卷]已知S,A,B,C是球O表面上的点,SA⊥平面ABC,AB⊥BC,SA=AB=1,BC= ,则球O的表面积等于( )
A.4π B.3π C.2π D.π
【分析】根据条件,确定球O的位置,并求出球半径.
考点3 球的表面积、体积
返回目录
【解析】如图所示,A,B,C三点在一小圆面上,
∵AB⊥BC,AC为斜边,
∴小圆的圆心为AC的中点D.
∵SA=AB=1,BC=2,
∴AC= ,AD= .
∵S,A,B,C都在球面上,取SC的中点O,则OD∥SA.
∵SA⊥平面ABC,∴OD⊥平面ABC,
∴O为球心,SO为半径.
∵SC= =2,∴SO=1,
∴球O的表面积为4π.
返回目录
本题考查球的几何性质及表面积公式,考查运算求解能力,考查数形结合、转化与化归思想,难度较大.
返回目录
在球心同侧有相距9 cm的两个平行截面,它们的面积分别为49π cm2和400π cm2.求球的表面积.
【解析】如图为球的轴截面,由球的截面性质知,AO1∥BO2,且O1,O2分别为两截面圆的圆心,则OO1⊥AO1,OO2⊥BO2,设球的半径为R.
返回目录
∵π·O2B2=49π,∴O2B=7(cm).
∵π·O1A2=400π,∴O1A=20(cm).
设OO1=x cm,则OO2=(x+9) cm.
在Rt△OO1A中,R2=x2+202.
在Rt△OO2B中,R2=(x+9)2+72,
∴x2+202=72+(x+9)2,
解得x=15,
∴R2=x2+202=252,∴R=25.
∴S球=4πR2=2 500π(cm2).
∴球的表面积为2 500π cm2.
返回目录
1.对于基本概念和能用公式直接求出棱柱、棱锥、棱台与球的表面积的问题,要结合它们的结构特点与平面几何知识来解决,这种题目难度不大.
2.要注意将空间问题转化为平面问题.
3.当给出的几何体比较复杂,有关的计算公式无法运用,或者虽然几何体并不复杂,但条件中的已知元素彼此离散时,我们可采用“割”、“补”的技巧,化复杂几何体为简单几何体(柱、锥、台),或化离散为集中,给解题提供便利.
返回目录
4.与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形 , 明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图 ,如球内切于正方体 ,切点为正方体各个面 的 中心,正方体的棱长等于球的直 径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线等于球的直径.球与旋转体的组合,通常作它们的轴截面进行解题,球与多面体的组合,通过多面体的一条侧棱和球心,或“切点”“接点”作出截面图.
返回目录
