2012届高考数学文科一轮复习精选课件(新人教a版):7.4 空间中的平行关系
文档属性
| 名称 | 2012届高考数学文科一轮复习精选课件(新人教a版):7.4 空间中的平行关系 |  | |
| 格式 | rar | ||
| 文件大小 | 825.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-06-15 18:39:20 | ||
图片预览










文档简介
(共31张PPT)
学案4 空间中的平行关系
考点1
考点2
考点3
填填知学情
课内考点突破
规 律 探 究
考 纲 解 读
考 向 预 测
考点4
返回目录
考 纲 解 读
空间中的平行关系 1.通过直观感知、操作确认,归纳出直线与平面平行、平面与平面平行的判定定理.
2.通过直观感知、操作确认,归纳出直线与平面平行、平面与平面平行的性质定理并加以证明.
空间线线平行、线面平行、面面平行的判断证明除在客观试题中以命题真假判断形式出现外,多数在解答题中考查,难度不大,一般利用判定定理或性质定理即可证明.
考 向 预 测
返回目录
1.直线与平面平行的判定和性质
(1)判定定理
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.可以用符号表示为 .
(2)性质定理
一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.可以用符号表示为 .
a?α,b?α,且a∥b? a∥α
a∥α,a?β,α∩β=b ?a∥b
返回目录
2.平面与平面平行的判定和性质
(1)判定定理
一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.可以用符号表示
为 .
a?α,b?α,a∩b=P,a∥β,b∥β?α∥β
(2)性质定理
如果两个平行平面同时和第三个平面相交,那么它们的交线平行.
返回目录
考点1 平行的基本问题
[2009年高考福建卷]设m,n是平面α内的两条不同直线,l1,l2是平面β内的两条相交直线,则α∥β的一个充分而不必要条件是( )
A.m∥β且l1∥α B.m∥l1且n∥l2
C.m∥β且n∥β D.m∥β且n∥l2
返回目录
【解析】∵m∥l1,且n∥l2,又l1,l2是平面β内的两条相
交直线,∴α∥β,而当α∥β时不一定推出m∥l1且n∥l2.
故应选B.
【分析】把选项逐个代入检验.
返回目录
本考点主要在客观试题中考查线面平行、面面平行的判定与性质的应用,作为客观试题判断每一个命题时,一是要注意判定与性质定理中易忽视的条件,如线面平行,需条件线在面外;二是结合题意作出图形;三会举反例或反证法推断命题是否正确.
返回目录
α,β,γ是三个平面,a,b是两条直线,有下列三个条件:
①a∥γ,b?β;②a∥γ,b∥β;③b∥β,a?γ.
如果命题“α∩β=a,b?γ,且 ,则a∥b”为真命题,则可以在横线处填入的条件是( )
A.①或② B.②或③ C.①或③ D.只有②
返回目录
【解析】①中,a∥γ,a?β,b?β,β∩γ=b?a∥b
(线面平行的性质).③中,b∥β,b?γ,a?γ,
β∩γ=a?a∥b(线面平行的性质).
故应选C.
返回目录
考点2 直线与平面平行的判定
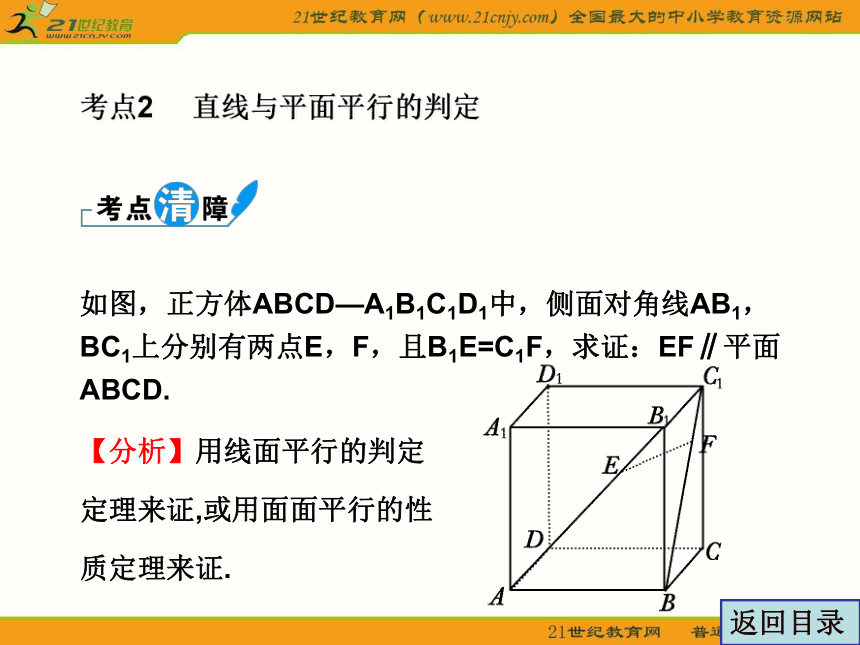
如图,正方体ABCD—A1B1C1D1中,侧面对角线AB1,BC1上分别有两点E,F,且B1E=C1F,求证:EF∥平面ABCD.
【分析】用线面平行的判定
定理来证,或用面面平行的性
质定理来证.
返回目录
【证明】证法一:分别过E,F作EM⊥AB于M, FN⊥BC于N,连结MN.
∵BB1⊥平面ABCD,
∴BB1⊥AB,BB1⊥BC,
∴EM∥BB1,FN∥BB1,
∴EM∥FN.
又B1E=C1F,∴EM=FN,
故四边形MNFE是平行四边形,
∴EF∥MN.
又MN在平面ABCD中,
∴EF∥平面ABCD.
返回目录
证法二:过E作EG∥AB交BB1于G,连结GF,
则 ,
∵B1E=C1F,B1A=C1B,
∴ ,
∴FG∥B1C1∥BC.
又EG∩FG=G,AB∩BC=B,
∴平面EFG∥平面ABCD,
而EF?平面EFG,
∴EF∥平面ABCD.
返回目录
判断或证明线面平行的常用方法有:①利用线面平行的定义(无公共点);②利用线面平行的判定定理(a? α,b? α,a∥b ?a∥ α);③利用面面平行的性质定理(α∥ β,a? α? a∥ β);④利用面面平行的性质(α∥β,a / α,a /β ,a ∥α ? a∥β).
返回目录
如图 所示,矩形ABCD和梯形BEFC有公共边BC,BE∥CF,∠BCF=90°,求证:AE∥平面DCF.
返回目录
【证明】过点E作EG⊥CF交CF于G,连结DG,可得四边形BCGE为矩形.
又ABCD为矩形,
所以AD EG,
从而四边形ADGE为平行四边形,
故AE∥DG.
因为AE?平面DCF,DG?平面DCF,
所以AE∥平面DCF.
返回目录
求证:若两个相交平面都平行于一条直线,则它们的交线也平行于这条直线.
考点3 直线与平面平行的性质及应用
【分析】利用线面平行的性质定理可证线线平行.
返回目录
【解析】已知:α∩β=b,α∥a,β∥a,求证:a∥b.
证明:证法一:如图,过a作平面γ∩α=c,由a∥α得a∥c. 同理过a作平面δ∩β=d,则a∥d,于是c∥d.又c?β,d?β,所以c∥β.又α∩β=b,c?α,所以c∥b.又a∥c,所以a∥b.
返回目录
证法二:如图,在b上任取一点A,过A和a作平面和α相交于l1,和β相交于l2,因为a∥α,所以a∥l1.
因为a∥β,所以a∥l2.
但过一点只能作一条
直线与另一条直线平
行,所以l1与l2重合.
又因为l1?α,l2?β,
所以l1和l1重合于b,
所以a∥b.
返回目录
应用线面平行的性质定理时,应着力寻找过已知直线的平面与已知平面的交线,有时为了得到交线还需作出辅助平面.证法二中用到了结论“过直线外一点有且只有一条直线和这条直线平行”.
返回目录
如图,四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证:AP∥GH.
【证明】如图,连接AC交BD于O,连接MO.
∵四边形ABCD是平行四边形,
∴O是AC中点,又M是PC的中点,
∴AP∥OM.
则有PA∥平面BMD.
(根据直线和平面平行的判定定理)
∵平面PAHG∩平面BMD=GH,
∴PA∥GH.(根据直线和平面平行的性质定理)
返回目录
如图,已知ABCD—A1B1C1D1
是棱长为3的正方体,点E在AA1上,
点F在CC1上,点G在BB1上,且
AE=FC1=B1G=1,H是B1C1的中点.
(1)求证:E,B,F,D1四点共面;
(2)求证:平面A1GH∥平面BED1F.
考点4 面面平行的判定与性质
返回目录
【证明】(1)∵AE=B1G=1,∴BG=A1E=2,
∴BG A1E,∴A1G∥BE.
又同理,C1F B1G,
∴四边形C1FGB1是平行四边形,
∴FG C1B1 D1A1,
∴四边形A1GFD1是平行四边形.
∴A1G D1F,∴D1F EB,
故E,B,F,D1四点共面.
【分析】(1)只需证明BE∥D1F或BF∥D1E,即可证明B,E,D1,F共面;
(2)利用面面平行的判定条件证明.
返回目录
(2)∵H是B1C1的中点,∴B1H= .
又B1G=1,∴ .
又 ,且∠FCB=∠GB1H=90°,
∴△B1HG∽△CBF,
∴∠B1GH=∠CFB=∠FBG,
∴HG∥FB.
又由(1)知A1G∥BE,且HG∩A1G=G,FB∩BE=B,
∴平面A1GH∥平面BED1F.
返回目录
平面与平面平行问题
(1)在平面和平面平行的判定定理中,“两条相交直线”中的“相交”两个字不能忽略,否则结论不一定成立.
(2)若由两个平面平行来推证两条直线平行,则这两条直线必须是这两个平行平面与第三个平面的交线,有时候第三个平面需要作出来.
(3)平面与平面平行的判定方法
①依定义,采用反证法.
②用判定定理及推论.
③用“垂直于同一条直线的两个平面平行”这一性质证明.
返回目录
如图,已知α∥β,异面直线AB,CD和平面α,β分别交于A,B,C,D四点,E,F,G,H分别是AB,BC,CD,DA的中点.求证:
(1)E,F,G,H共面;
(2)平面EFGH∥平面α.
返回目录
【证明】(1)∵E,H分别是AB,DA的中点,
∴EH∥BD且EH= BD.
同理,FG∥BD且FG= BD,∴FG∥EH且FG=EH.
∴四边形EFGH是平行四边形,即E,F,G,H共面.
返回目录
(2)平面ABD和平面α有一个公共点A,设两平面交于过点A的直线AD′.
∵α∥β,∴AD′∥BD.
又∵BD∥EH,∴EH∥BD∥AD′.∴EH∥平面α,EH∥平面β.
同理,EF∥平面α,EF∥平面β.
∴平面EFGH∥平面α.
返回目录
1.在证明平行关系时,要注意此类问题的通性通法、相关题型及常用解题思路方法,在作辅助线或辅助面时,要有理有据,不能随意作,辅助线、辅助面具有的性质,一定要以某一性质定理为依据,不能主观臆断.
返回目录
2.本学案应注重线线平行、线面平行、面面平行的相互转换.
返回目录
学案4 空间中的平行关系
考点1
考点2
考点3
填填知学情
课内考点突破
规 律 探 究
考 纲 解 读
考 向 预 测
考点4
返回目录
考 纲 解 读
空间中的平行关系 1.通过直观感知、操作确认,归纳出直线与平面平行、平面与平面平行的判定定理.
2.通过直观感知、操作确认,归纳出直线与平面平行、平面与平面平行的性质定理并加以证明.
空间线线平行、线面平行、面面平行的判断证明除在客观试题中以命题真假判断形式出现外,多数在解答题中考查,难度不大,一般利用判定定理或性质定理即可证明.
考 向 预 测
返回目录
1.直线与平面平行的判定和性质
(1)判定定理
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.可以用符号表示为 .
(2)性质定理
一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.可以用符号表示为 .
a?α,b?α,且a∥b? a∥α
a∥α,a?β,α∩β=b ?a∥b
返回目录
2.平面与平面平行的判定和性质
(1)判定定理
一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.可以用符号表示
为 .
a?α,b?α,a∩b=P,a∥β,b∥β?α∥β
(2)性质定理
如果两个平行平面同时和第三个平面相交,那么它们的交线平行.
返回目录
考点1 平行的基本问题
[2009年高考福建卷]设m,n是平面α内的两条不同直线,l1,l2是平面β内的两条相交直线,则α∥β的一个充分而不必要条件是( )
A.m∥β且l1∥α B.m∥l1且n∥l2
C.m∥β且n∥β D.m∥β且n∥l2
返回目录
【解析】∵m∥l1,且n∥l2,又l1,l2是平面β内的两条相
交直线,∴α∥β,而当α∥β时不一定推出m∥l1且n∥l2.
故应选B.
【分析】把选项逐个代入检验.
返回目录
本考点主要在客观试题中考查线面平行、面面平行的判定与性质的应用,作为客观试题判断每一个命题时,一是要注意判定与性质定理中易忽视的条件,如线面平行,需条件线在面外;二是结合题意作出图形;三会举反例或反证法推断命题是否正确.
返回目录
α,β,γ是三个平面,a,b是两条直线,有下列三个条件:
①a∥γ,b?β;②a∥γ,b∥β;③b∥β,a?γ.
如果命题“α∩β=a,b?γ,且 ,则a∥b”为真命题,则可以在横线处填入的条件是( )
A.①或② B.②或③ C.①或③ D.只有②
返回目录
【解析】①中,a∥γ,a?β,b?β,β∩γ=b?a∥b
(线面平行的性质).③中,b∥β,b?γ,a?γ,
β∩γ=a?a∥b(线面平行的性质).
故应选C.
返回目录
考点2 直线与平面平行的判定
如图,正方体ABCD—A1B1C1D1中,侧面对角线AB1,BC1上分别有两点E,F,且B1E=C1F,求证:EF∥平面ABCD.
【分析】用线面平行的判定
定理来证,或用面面平行的性
质定理来证.
返回目录
【证明】证法一:分别过E,F作EM⊥AB于M, FN⊥BC于N,连结MN.
∵BB1⊥平面ABCD,
∴BB1⊥AB,BB1⊥BC,
∴EM∥BB1,FN∥BB1,
∴EM∥FN.
又B1E=C1F,∴EM=FN,
故四边形MNFE是平行四边形,
∴EF∥MN.
又MN在平面ABCD中,
∴EF∥平面ABCD.
返回目录
证法二:过E作EG∥AB交BB1于G,连结GF,
则 ,
∵B1E=C1F,B1A=C1B,
∴ ,
∴FG∥B1C1∥BC.
又EG∩FG=G,AB∩BC=B,
∴平面EFG∥平面ABCD,
而EF?平面EFG,
∴EF∥平面ABCD.
返回目录
判断或证明线面平行的常用方法有:①利用线面平行的定义(无公共点);②利用线面平行的判定定理(a? α,b? α,a∥b ?a∥ α);③利用面面平行的性质定理(α∥ β,a? α? a∥ β);④利用面面平行的性质(α∥β,a / α,a /β ,a ∥α ? a∥β).
返回目录
如图 所示,矩形ABCD和梯形BEFC有公共边BC,BE∥CF,∠BCF=90°,求证:AE∥平面DCF.
返回目录
【证明】过点E作EG⊥CF交CF于G,连结DG,可得四边形BCGE为矩形.
又ABCD为矩形,
所以AD EG,
从而四边形ADGE为平行四边形,
故AE∥DG.
因为AE?平面DCF,DG?平面DCF,
所以AE∥平面DCF.
返回目录
求证:若两个相交平面都平行于一条直线,则它们的交线也平行于这条直线.
考点3 直线与平面平行的性质及应用
【分析】利用线面平行的性质定理可证线线平行.
返回目录
【解析】已知:α∩β=b,α∥a,β∥a,求证:a∥b.
证明:证法一:如图,过a作平面γ∩α=c,由a∥α得a∥c. 同理过a作平面δ∩β=d,则a∥d,于是c∥d.又c?β,d?β,所以c∥β.又α∩β=b,c?α,所以c∥b.又a∥c,所以a∥b.
返回目录
证法二:如图,在b上任取一点A,过A和a作平面和α相交于l1,和β相交于l2,因为a∥α,所以a∥l1.
因为a∥β,所以a∥l2.
但过一点只能作一条
直线与另一条直线平
行,所以l1与l2重合.
又因为l1?α,l2?β,
所以l1和l1重合于b,
所以a∥b.
返回目录
应用线面平行的性质定理时,应着力寻找过已知直线的平面与已知平面的交线,有时为了得到交线还需作出辅助平面.证法二中用到了结论“过直线外一点有且只有一条直线和这条直线平行”.
返回目录
如图,四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证:AP∥GH.
【证明】如图,连接AC交BD于O,连接MO.
∵四边形ABCD是平行四边形,
∴O是AC中点,又M是PC的中点,
∴AP∥OM.
则有PA∥平面BMD.
(根据直线和平面平行的判定定理)
∵平面PAHG∩平面BMD=GH,
∴PA∥GH.(根据直线和平面平行的性质定理)
返回目录
如图,已知ABCD—A1B1C1D1
是棱长为3的正方体,点E在AA1上,
点F在CC1上,点G在BB1上,且
AE=FC1=B1G=1,H是B1C1的中点.
(1)求证:E,B,F,D1四点共面;
(2)求证:平面A1GH∥平面BED1F.
考点4 面面平行的判定与性质
返回目录
【证明】(1)∵AE=B1G=1,∴BG=A1E=2,
∴BG A1E,∴A1G∥BE.
又同理,C1F B1G,
∴四边形C1FGB1是平行四边形,
∴FG C1B1 D1A1,
∴四边形A1GFD1是平行四边形.
∴A1G D1F,∴D1F EB,
故E,B,F,D1四点共面.
【分析】(1)只需证明BE∥D1F或BF∥D1E,即可证明B,E,D1,F共面;
(2)利用面面平行的判定条件证明.
返回目录
(2)∵H是B1C1的中点,∴B1H= .
又B1G=1,∴ .
又 ,且∠FCB=∠GB1H=90°,
∴△B1HG∽△CBF,
∴∠B1GH=∠CFB=∠FBG,
∴HG∥FB.
又由(1)知A1G∥BE,且HG∩A1G=G,FB∩BE=B,
∴平面A1GH∥平面BED1F.
返回目录
平面与平面平行问题
(1)在平面和平面平行的判定定理中,“两条相交直线”中的“相交”两个字不能忽略,否则结论不一定成立.
(2)若由两个平面平行来推证两条直线平行,则这两条直线必须是这两个平行平面与第三个平面的交线,有时候第三个平面需要作出来.
(3)平面与平面平行的判定方法
①依定义,采用反证法.
②用判定定理及推论.
③用“垂直于同一条直线的两个平面平行”这一性质证明.
返回目录
如图,已知α∥β,异面直线AB,CD和平面α,β分别交于A,B,C,D四点,E,F,G,H分别是AB,BC,CD,DA的中点.求证:
(1)E,F,G,H共面;
(2)平面EFGH∥平面α.
返回目录
【证明】(1)∵E,H分别是AB,DA的中点,
∴EH∥BD且EH= BD.
同理,FG∥BD且FG= BD,∴FG∥EH且FG=EH.
∴四边形EFGH是平行四边形,即E,F,G,H共面.
返回目录
(2)平面ABD和平面α有一个公共点A,设两平面交于过点A的直线AD′.
∵α∥β,∴AD′∥BD.
又∵BD∥EH,∴EH∥BD∥AD′.∴EH∥平面α,EH∥平面β.
同理,EF∥平面α,EF∥平面β.
∴平面EFGH∥平面α.
返回目录
1.在证明平行关系时,要注意此类问题的通性通法、相关题型及常用解题思路方法,在作辅助线或辅助面时,要有理有据,不能随意作,辅助线、辅助面具有的性质,一定要以某一性质定理为依据,不能主观臆断.
返回目录
2.本学案应注重线线平行、线面平行、面面平行的相互转换.
返回目录
