2012届高考数学文科一轮复习精选课件(新人教a版):第5章 不等5.1 不等关系与不等式
文档属性
| 名称 | 2012届高考数学文科一轮复习精选课件(新人教a版):第5章 不等5.1 不等关系与不等式 |  | |
| 格式 | rar | ||
| 文件大小 | 868.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-06-15 18:39:20 | ||
图片预览









文档简介
(共32张PPT)
学案1 不等关系与不等式
考点1
考点2
考点3
考点4
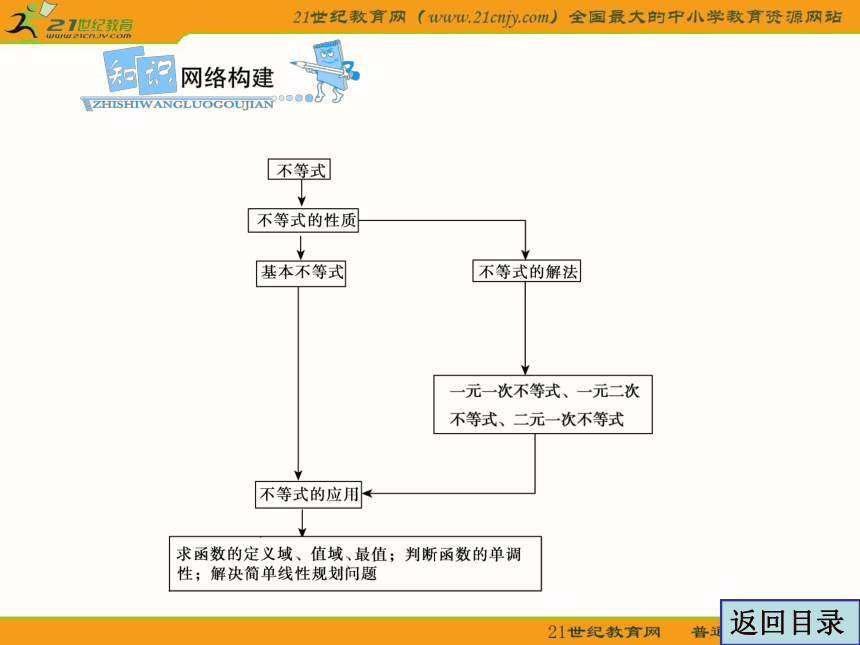
知识网络构建
填填知学情
课内考点突破
规 律 探 究
考 纲 解 读
考 向 预 测
返回目录
返回目录
考 纲 解 读
不等关系与不等式 1.了解现实世界和日常生活中的不等关系,了解不等式(组)的实际背景.
返回目录
考 向 预 测
纵观近三年新课标区高考可以发现,由于新课程标准对不等式的性质要求不高,高考也几乎没有单独命题,作差法比较两实数大小也仅是解决问题的工具,一般不单独命题,高考对本学案知识的考查往往结合函数的性质,利用函数中的不等关系比较实数的大小.
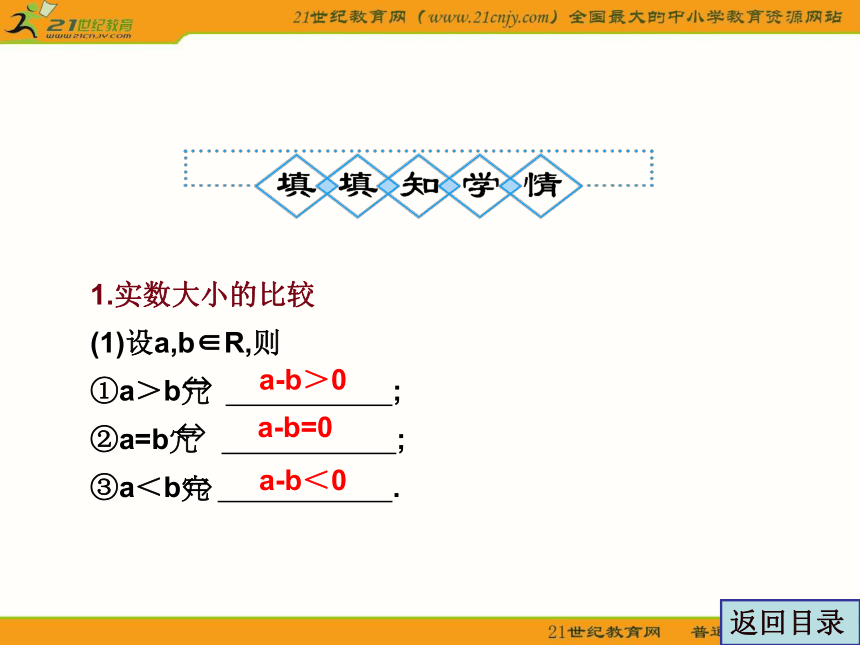
1.实数大小的比较
(1)设a,b∈R,则
①a>b? ;
②a=b? ;
③a<b? .
返回目录
a-b>0
a-b=0
a-b<0
返回目录
3.不等式的性质
(1) a>b? (对称性).
(2) a>b,b>c? (传递性).
(3)a>b? ;
(4) a>b,c>0? ;
a>b,c<0? ;
(5)a>b ,c>d ;
b<a
a>c
a+c>b+c
a+c>b+d
ac<bc
ac>bc
(6) a>b>0,c>d>0 (可乘性).
(7) a>b>0? (n∈N*)(乘方性).
(8) a>b>0= (n∈N*)(开方性).
返回目录
an>bn
ac>bd
返回目录
考点1 不等式的概念与性质
[2010年高考江西卷]对于实数a,b,c,“a>b”是“ac2>bc2”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
返回目录
【分析】本题利用不等式的性质及充要条件的判定直接作出判断.
【解析】a>b?/ ac2>bc2,原因是c可能为0,而若ac2>bc2,则可推出a>b.
故“a>b”是“ac2>bc2”的必要不充分条件.
故应选B.
(1)准确记忆各性质成立的条件, 是正确应用性质的前提.
(2)在不等关系的判断中,特殊值法也是非常有效的方法.
返回目录
返回目录
[2010年高考广东卷]“x>0”是“ ”成立的 ( )
A.充分非必要条件 B.必要非充分条件
C.非充分非必要条件 D.充要条件
返回目录
【答案】A
【解析】因为当x>0时,一定有 ,但当 时,x<0也成立,因此x>0是 成立的充分不必要条件.
故应选A.
返回目录
考点2 应用不等式表示不等关系
某汽车公司由于发展的需要需购进一批汽车,计划使用不超过1 000万元的资金购买单价分别为40万元,90万元的A型汽车和B型汽车.根据需要,A型汽车至少买5辆,B型汽车至少买6辆,写出满足上述所有不等关系的不等式.
【分析】把握关键点,不超过1 000万元,且A,B两种车型分别至少5辆,6辆,则不等关系不难表示,要注意取值范围.
返回目录
【解析】设购买A型汽车和B型汽车分别为x辆,y辆,则 40x+90y≤1 000
x≥5
y≥6
x,y∈N+,
4x+9y≤100
x≥5
y≥6
x,y∈N+.
即
返回目录
注意区分“不等关系”和“不等式”的异同,不等关系强调的是关系,可用“>”“<”“≥”“≤”“≠”表示,不等式则是表现不等关系的式子,对于实际问题中的不等式关系可以从“不超过”“至少”“至多”等关键词上去把握,并考虑到实际意义.
返回目录
某矿山车队有4辆载重为10 t的甲型卡车和7辆载重为6 t的乙型卡车,有9名驾驶员.该车队每天至少要运360 t矿石至冶炼厂.已知甲型卡车每辆每天可往返6次,乙型卡车每辆每天可往返8次,写出满足上述所有不等关系的不等式.
返回目录
【解析】设每天派出甲型卡车x辆,乙型卡车y辆,根据题意,应有如下的不等关系:
(1)甲型卡车和乙型卡车的总和不能超过驾驶员人数;
(2)车队每天至少要运360 t矿石;
(3)甲型卡车不能超过4辆,乙型卡车不能超过7辆.
用关于x,y的不等式表示上述不等关系即可.
返回目录
5x+4y≥30
0≤x≤4
0≤y≤7
x,y∈N.
即
x+y≤9
10×6x+6×8y≥360
0≤x≤4
0≤y≤7
x,y∈N,即x+y≤9
返回目录
考点3 大小比较
设x+y<0,试比较(x2+y2)(x-y)与(x2+y2)· (x+y)
的大小;
(2)已知a>0,b>0,且a≠b,试比较aabb与(ab) 的大小.
返回目录
【分析】比较两数(或两式)的大小,一般用比较法,具体用作差比较还是用作商比较应由数(或式)特点而定.
【解析】 (1)(x2+y2)(x-y)-(x2-y2)(x+y)
=(x-y)[(x2+y2)-(x+y)2]
=-2xy(x-y).
∵x∴-2xy(x-y)>0,
∴(x2+y2)(x-y)>(x2-y2)(x+y).
返回目录
(2)若a>b>0,则 >1,a-b>0.
由指数函数的性质 >1.
若b>a>0,则0< <1,a-b<0.
由指数函数的性质 >1.
∴ >1, ∴ .
返回目录
(1)比较两个代数式的大小,可以根据它们的差的符号进行判断,一方面注意题目本身提供的字母的取值范围,另一方面通常将两代数式的差进行因式分解转化为多个因式相乘,或通过配方转化为几个非负实数之和,然后判断正负.
(2)作商比较通常适用于两代数式同号的情形.
返回目录
比较下列各组中两个代数式的大小:
(1)(x-3)2与(x-2)(x-4);
(2)当x>1时,x3与x2-x+1;
(3) + 与2+ .
返回目录
【解析】 (1)(x-3)2-(x-2)(x-4)=x2-6x+9-(x2-6x+8)=1>0,
∴(x-3)2>(x-2)(x-4).
(2)x3-(x2-x+1)=x3-x2+x-1
=x2(x-1)+(x-1)=(x-1)(x2+1),
∵x>1,∴x3-(x2-x+1)>0,∴当x>1时,x3>x2-x+1.
(3)∵ ,
∴ =
返回目录
考点4 范围问题
已知-1<a+b<3且2<a-b<4,求2a+3b的取值范围.
【分析】将2a+3b用a+b和a-b表示出来,再利用不等式的性质求解2a+3b的范围.
返回目录
【解析】设2a+3b=m(a+b)+n(a-b),
∴ m+n=2
m-n=3,
∴m= ,n= .
∴2a+3b= (a+b) (a-b).
∵-1<a+b<3,2<a-b<4,
∴ < (a+b)< ,-2< (a-b)<-1,
∴ < (a+b) (a-b)< ,
即 <2a+3b< .
返回目录
由a<f1(x1,y1)<b,c<f2(x1,y1)<d,求g(x1,y1)的取值范围,可利用待定系数法解决,即设g(x1,y1)=pf1(x1,y1)+qf2(x1,y1),用恒等变形求得p,q,再利用不等式的性质求得g(x1,y1)的范围.此外,本题也可用线性规划的方法来求解.
返回目录
设f(x)=ax2+bx且1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围.
【解析】解法一:设f(-2)=mf(-1)+nf(1)(m,n为待定系数),则4a-2b=m(a-b)+n(a+b),
即4a-2b=(m+n)a+(n-m)b.
m+n=4
n-m=-2,
m=3
n=1,
解得
于是得
返回目录
∴f(-2)=3f(-1)+f(1).
又1≤f(-1)≤2,2≤f(1)≤4,
∴5≤3f(-1)+f(1)≤10,故5≤f(-2)≤10.
解法二:由 f(-1)=a-b
f(1)=a+b,
a= [f(-1)+f(1)]
b= [f(1)-f(-1)],
∴f(-2)=4a-2b=3f(-1)+f(1).
又∵1≤f(-1)≤2,2≤f(1)≤4,
得
返回目录
∴5≤3f(-1)+f(1)≤10,故5≤f(-2)≤10.
解法三:由 1≤a-b≤2
2≤a+b≤4 确定的平面区域如图.
当f(-2)=4a-2b过点A ( ) 时,
取得最小值4× -2× =5,
当f(-2)=4a-2b过点B(3,1)时,
取得最大值4×3-2×1=10,
∴5≤f(-2)≤10.
返回目录
1.要注意不等式性质成立的条件.例如,重要结论:a>b,ab>0? ,不能弱化条件得a>b ,也不能强化条件得a>b>0? .
2.要正确处理带等号的情况.如由a>b,b≥c或a≥b,b>c均可得出a>c;而由a≥b,b≥c可能有a>c,也可能有a=c,当且仅当a=b且b=c时,才会有a=c.
3.两不等式相加的前提是两不等式必须同向,如“>”与“>”,“>”与“≥”均可理解成同向;两不等式相乘除了要同向外,还必须满足各数均是非负的.原则上不等式不能相减或相除.
学案1 不等关系与不等式
考点1
考点2
考点3
考点4
知识网络构建
填填知学情
课内考点突破
规 律 探 究
考 纲 解 读
考 向 预 测
返回目录
返回目录
考 纲 解 读
不等关系与不等式 1.了解现实世界和日常生活中的不等关系,了解不等式(组)的实际背景.
返回目录
考 向 预 测
纵观近三年新课标区高考可以发现,由于新课程标准对不等式的性质要求不高,高考也几乎没有单独命题,作差法比较两实数大小也仅是解决问题的工具,一般不单独命题,高考对本学案知识的考查往往结合函数的性质,利用函数中的不等关系比较实数的大小.
1.实数大小的比较
(1)设a,b∈R,则
①a>b? ;
②a=b? ;
③a<b? .
返回目录
a-b>0
a-b=0
a-b<0
返回目录
3.不等式的性质
(1) a>b? (对称性).
(2) a>b,b>c? (传递性).
(3)a>b? ;
(4) a>b,c>0? ;
a>b,c<0? ;
(5)a>b ,c>d ;
b<a
a>c
a+c>b+c
a+c>b+d
ac<bc
ac>bc
(6) a>b>0,c>d>0 (可乘性).
(7) a>b>0? (n∈N*)(乘方性).
(8) a>b>0= (n∈N*)(开方性).
返回目录
an>bn
ac>bd
返回目录
考点1 不等式的概念与性质
[2010年高考江西卷]对于实数a,b,c,“a>b”是“ac2>bc2”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
返回目录
【分析】本题利用不等式的性质及充要条件的判定直接作出判断.
【解析】a>b?/ ac2>bc2,原因是c可能为0,而若ac2>bc2,则可推出a>b.
故“a>b”是“ac2>bc2”的必要不充分条件.
故应选B.
(1)准确记忆各性质成立的条件, 是正确应用性质的前提.
(2)在不等关系的判断中,特殊值法也是非常有效的方法.
返回目录
返回目录
[2010年高考广东卷]“x>0”是“ ”成立的 ( )
A.充分非必要条件 B.必要非充分条件
C.非充分非必要条件 D.充要条件
返回目录
【答案】A
【解析】因为当x>0时,一定有 ,但当 时,x<0也成立,因此x>0是 成立的充分不必要条件.
故应选A.
返回目录
考点2 应用不等式表示不等关系
某汽车公司由于发展的需要需购进一批汽车,计划使用不超过1 000万元的资金购买单价分别为40万元,90万元的A型汽车和B型汽车.根据需要,A型汽车至少买5辆,B型汽车至少买6辆,写出满足上述所有不等关系的不等式.
【分析】把握关键点,不超过1 000万元,且A,B两种车型分别至少5辆,6辆,则不等关系不难表示,要注意取值范围.
返回目录
【解析】设购买A型汽车和B型汽车分别为x辆,y辆,则 40x+90y≤1 000
x≥5
y≥6
x,y∈N+,
4x+9y≤100
x≥5
y≥6
x,y∈N+.
即
返回目录
注意区分“不等关系”和“不等式”的异同,不等关系强调的是关系,可用“>”“<”“≥”“≤”“≠”表示,不等式则是表现不等关系的式子,对于实际问题中的不等式关系可以从“不超过”“至少”“至多”等关键词上去把握,并考虑到实际意义.
返回目录
某矿山车队有4辆载重为10 t的甲型卡车和7辆载重为6 t的乙型卡车,有9名驾驶员.该车队每天至少要运360 t矿石至冶炼厂.已知甲型卡车每辆每天可往返6次,乙型卡车每辆每天可往返8次,写出满足上述所有不等关系的不等式.
返回目录
【解析】设每天派出甲型卡车x辆,乙型卡车y辆,根据题意,应有如下的不等关系:
(1)甲型卡车和乙型卡车的总和不能超过驾驶员人数;
(2)车队每天至少要运360 t矿石;
(3)甲型卡车不能超过4辆,乙型卡车不能超过7辆.
用关于x,y的不等式表示上述不等关系即可.
返回目录
5x+4y≥30
0≤x≤4
0≤y≤7
x,y∈N.
即
x+y≤9
10×6x+6×8y≥360
0≤x≤4
0≤y≤7
x,y∈N,即x+y≤9
返回目录
考点3 大小比较
设x+y<0,试比较(x2+y2)(x-y)与(x2+y2)· (x+y)
的大小;
(2)已知a>0,b>0,且a≠b,试比较aabb与(ab) 的大小.
返回目录
【分析】比较两数(或两式)的大小,一般用比较法,具体用作差比较还是用作商比较应由数(或式)特点而定.
【解析】 (1)(x2+y2)(x-y)-(x2-y2)(x+y)
=(x-y)[(x2+y2)-(x+y)2]
=-2xy(x-y).
∵x
∴(x2+y2)(x-y)>(x2-y2)(x+y).
返回目录
(2)若a>b>0,则 >1,a-b>0.
由指数函数的性质 >1.
若b>a>0,则0< <1,a-b<0.
由指数函数的性质 >1.
∴ >1, ∴ .
返回目录
(1)比较两个代数式的大小,可以根据它们的差的符号进行判断,一方面注意题目本身提供的字母的取值范围,另一方面通常将两代数式的差进行因式分解转化为多个因式相乘,或通过配方转化为几个非负实数之和,然后判断正负.
(2)作商比较通常适用于两代数式同号的情形.
返回目录
比较下列各组中两个代数式的大小:
(1)(x-3)2与(x-2)(x-4);
(2)当x>1时,x3与x2-x+1;
(3) + 与2+ .
返回目录
【解析】 (1)(x-3)2-(x-2)(x-4)=x2-6x+9-(x2-6x+8)=1>0,
∴(x-3)2>(x-2)(x-4).
(2)x3-(x2-x+1)=x3-x2+x-1
=x2(x-1)+(x-1)=(x-1)(x2+1),
∵x>1,∴x3-(x2-x+1)>0,∴当x>1时,x3>x2-x+1.
(3)∵ ,
∴ =
返回目录
考点4 范围问题
已知-1<a+b<3且2<a-b<4,求2a+3b的取值范围.
【分析】将2a+3b用a+b和a-b表示出来,再利用不等式的性质求解2a+3b的范围.
返回目录
【解析】设2a+3b=m(a+b)+n(a-b),
∴ m+n=2
m-n=3,
∴m= ,n= .
∴2a+3b= (a+b) (a-b).
∵-1<a+b<3,2<a-b<4,
∴ < (a+b)< ,-2< (a-b)<-1,
∴ < (a+b) (a-b)< ,
即 <2a+3b< .
返回目录
由a<f1(x1,y1)<b,c<f2(x1,y1)<d,求g(x1,y1)的取值范围,可利用待定系数法解决,即设g(x1,y1)=pf1(x1,y1)+qf2(x1,y1),用恒等变形求得p,q,再利用不等式的性质求得g(x1,y1)的范围.此外,本题也可用线性规划的方法来求解.
返回目录
设f(x)=ax2+bx且1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围.
【解析】解法一:设f(-2)=mf(-1)+nf(1)(m,n为待定系数),则4a-2b=m(a-b)+n(a+b),
即4a-2b=(m+n)a+(n-m)b.
m+n=4
n-m=-2,
m=3
n=1,
解得
于是得
返回目录
∴f(-2)=3f(-1)+f(1).
又1≤f(-1)≤2,2≤f(1)≤4,
∴5≤3f(-1)+f(1)≤10,故5≤f(-2)≤10.
解法二:由 f(-1)=a-b
f(1)=a+b,
a= [f(-1)+f(1)]
b= [f(1)-f(-1)],
∴f(-2)=4a-2b=3f(-1)+f(1).
又∵1≤f(-1)≤2,2≤f(1)≤4,
得
返回目录
∴5≤3f(-1)+f(1)≤10,故5≤f(-2)≤10.
解法三:由 1≤a-b≤2
2≤a+b≤4 确定的平面区域如图.
当f(-2)=4a-2b过点A ( ) 时,
取得最小值4× -2× =5,
当f(-2)=4a-2b过点B(3,1)时,
取得最大值4×3-2×1=10,
∴5≤f(-2)≤10.
返回目录
1.要注意不等式性质成立的条件.例如,重要结论:a>b,ab>0? ,不能弱化条件得a>b ,也不能强化条件得a>b>0? .
2.要正确处理带等号的情况.如由a>b,b≥c或a≥b,b>c均可得出a>c;而由a≥b,b≥c可能有a>c,也可能有a=c,当且仅当a=b且b=c时,才会有a=c.
3.两不等式相加的前提是两不等式必须同向,如“>”与“>”,“>”与“≥”均可理解成同向;两不等式相乘除了要同向外,还必须满足各数均是非负的.原则上不等式不能相减或相除.
